離散正交變換理論實例教學法的探索與實踐

王建衛

（東北林業大學 機電工程學院，黑龍江 哈爾濱 150040）

離散正交變換理論實例教學法的探索與實踐

王建衛

（東北林業大學 機電工程學院，黑龍江 哈爾濱 150040）

為了生動地講解枯燥的正交變換公式，探討了離散正交變換理論實例教學的重要性和具體實施方法.在教學環節中設計了2個典型的離散哈爾變換教學實例.在啟發學生繪制一維哈爾變換的快速算法流程圖基礎上，完成二維哈爾變換的計算問題，能夠讓學生理解離散正交變換計算的關鍵所在，有助于幫助學生深入地理解正交變換理論.實踐證明，離散正交變換理論的實例教學效果良好.

正交變換；離散哈爾變換；實例教學

目前大學所開設的主要數學課程包括高等數學、線性代數、概率論與數理統計、計算方法、復變函數與積分變換和離散數學等課程[1]，矩陣變換作為一個較為獨立的教學內容，在多門課程里都有不同程度的涉及.通常電子與信息類專業是以信號與信息處理作為主要的研究方向[2]，信號的各種變換是以矩陣變換為基礎的，因此，變換理論成為大學數學教學的重點內容是必然的.離散正交變換是矩陣變換的一種特殊形式，具有變換類型多，變換公式復雜，計算難度較大的特點，因此進行相應的教學方法探索是必要的[3].

典型的課堂教學方法有討論式教學法[4]、問題式教學法[5]和實例教學法[6]等.討論式教學法的核心是啟發學生就特定問題發表自己的見解，以培養學生獨立思考的能力和創新精神，適用于大學低年級的理論知識較淺的課程和高年級的應用類專業課程.問題式教學法的核心是以問題為導向充分發揮學生主觀能動性，適用于具有一定知識基礎的大學高年級的學生和設計類課程的課堂教學.實例教學法的核心是在教師指導下，根據課程教學目標和內容的需要，通過典型實例的分析和講解完成教學，這一教學方法在許多學科的教學工作中取得了良好的效果，適用于大學較低年級的學生和理論性較強課程的課堂教學.

離散正交變換理論公式枯燥，難以理解，在授課過程中發現存在學生理解不夠深刻，應用意識不強的問題.因此，本文以哈爾變換為例設計了2個典型的離散正交變換實例，對離散正交變換理論的實例法課堂教學進行了有益的探索與實踐.

1 離散正交變換理論教學內容分析

在電子信息類專業高年級的專業課授課中發現，離散正交變換理論是大學數學的一個不容忽略的重點和難點內容.在課堂講授過程中，必須進行特征向量變換、哈爾變換、沃爾什變換、哈達瑪變換、斜變換和余弦變換等幾種經典的離散正交變換理論公式的推導[7-8].在傳統的以講授理論為主的變換理論課堂教學中，由于變換理論教學內容的枯燥性，學生在聽講過程中會出現注意力不夠集中、聽不懂的情況，導致缺乏學習興趣，學習效果不佳.

為了提高學生的學習興趣，可以采用實例教學法進行授課.按照由淺入深、循序漸進的原則將離散正交變換理論的教學內容劃分為離散正交變換的定義、變換矩陣及其性質、快速算法和實例分析等4個基本點.

在授課過程中通過引導學生分析正交變換的定義，得出了“正交矩陣是正交變換定義的核心”的結論，調動了學生獨立思考新問題的積極性，也有助于培養學生的創新思維.

2 實例教學法在離散哈爾變換計算中的應用

在實例教學法的教學過程中，教師應精心選擇把抽象理論轉化到具體問題的實例，實例的選擇是否恰當將直接影響到教學效果[9].好的實例應滿足一般性、擴展性和啟發性的要求，離散正交變換教學過程中選擇實例的3個原則是：第一，選擇的變換類型要符合一維和二維離散正交變換的一般定義；第二，二維正交變換計算過程可分解為2次一維正交變換的計算，因此快速計算流程實例以一維正交變換為主，并可擴展得到二維正交變換計算的規律；第三，總結二維離散正交變換的計算過程，通過數據的重排和編程實現啟發學生思維，開拓計算思路，使實例具有普適性.根據這3個原則，離散正交變換理論的教學過程可分為教師講授正交矩陣，師生共同給出正交變換的定義，學生繪制快速算法流程圖并由教師規范作圖和指出離散哈爾變換的應用背景等4個遞進的環節.

以哈爾變換為例，介紹實例教學法在離散正交變換理論教學中的應用.

第1個環節是由教師講授哈爾矩陣的形式.連續哈爾函數的數學解析式經過離散化后可得到哈爾矩陣，在講解過程中，教師應注意對連續函數離散化的實質進行分析.

連續哈爾函數的定義（歸一化）為

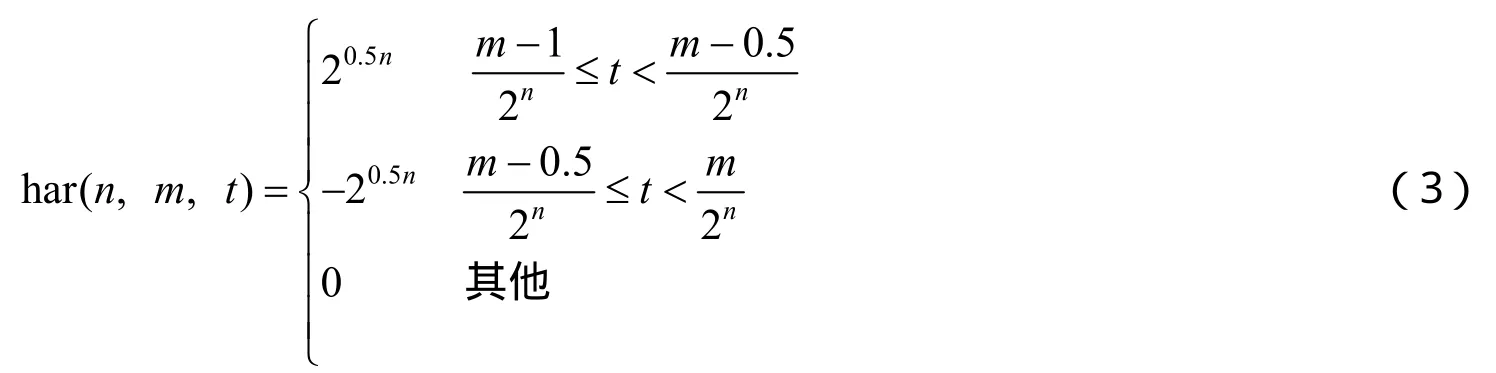
離散矩陣H(r)是由連續函數計算得到的，在講解時注意（N為連續哈爾函數圖形的取樣次數），其中：r為包含0階的總階數.

第2個環節是由教師給出哈爾變換的形式.在給出哈爾變換形式的教學過程中，教師應分析一維哈爾變換、二維哈爾變換以及正、逆變換公式的區別.

對于N維向量XN，一維哈爾正變換的計算公式為

一維哈爾逆變換的計算公式為

在課堂教學中，通過分析矩陣數據的特點，參考一維變換的形式，部分學生能夠較為準確地書寫二維變換公式.

對于NN階矩陣X，二維哈爾正變換的計算公式為

二維哈爾逆變換的計算公式為

分析式（4）～（7），師生共同總結出正變換矩陣不轉置，二維變換是2次一維運算的規律，這有助于學生在有限的課堂時間內更穩固地記憶公式，提高了課堂學習效率，節省了課余的復習時間.

第3個環節是面對簡單而內涵豐富的變換公式給出課前教師設計的實例，選擇計算公式，引導學生自己畫出快速算法流程圖，由教師總結規律并規范作圖.

例1 設計一維哈爾變換的快速算法流程圖.

例1是典型的快速算法流程圖的繪制問題，應從3個關鍵點進行詳細分析和講解.第1個關鍵點是由連續的哈爾函數確定矩陣H(2)；第2個關鍵點是將變換的計算公式表示為代數表達式；第3個關鍵點是化簡代數表達式.

由式（4）可知，當N4時，一階哈爾正變換的計算公式為

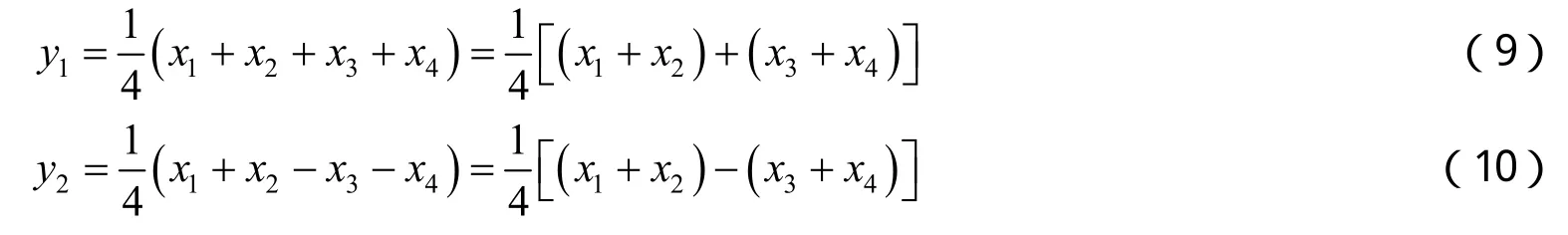
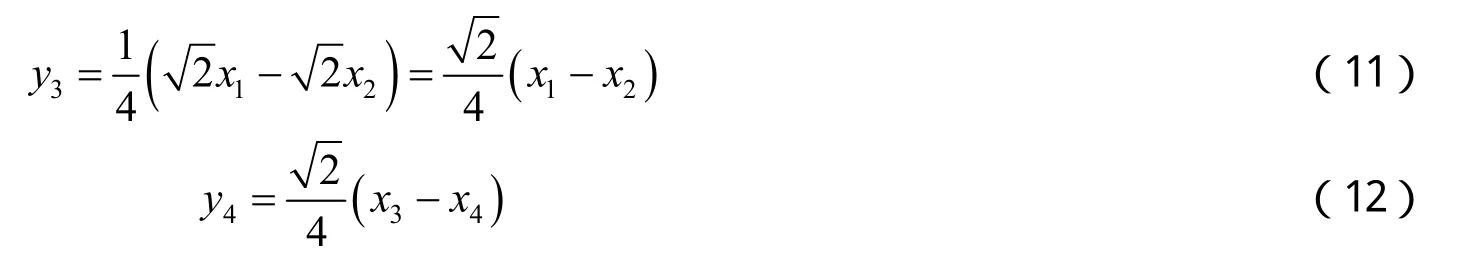
由式（9）～（12），按照由左至右、由上至下的原則教師板書繪制快速算法流程圖（見圖1）.

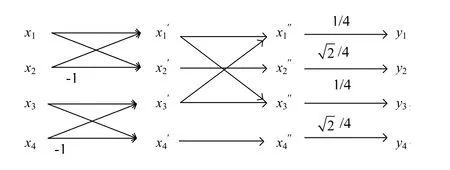
圖1 一維哈爾正變換的快速算法流程圖

參考一維哈爾正變換快速流程圖，課堂上學生基本上能根據式（5）繪制出逆變換的快速算法流程圖（見圖2）.

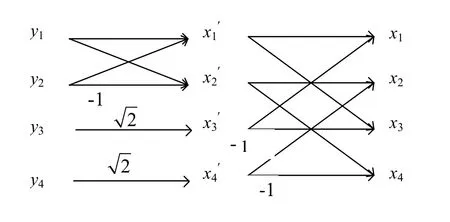
圖2 一維哈爾逆變換的快速算法流程圖

通過引導學生繪制一維哈爾變換的快速算法流程圖，使哈爾變換的代數表達式成為簡單的計算流程，基本要點是保存中間結果，避免重復運算，有助于幫助學生深入理解快速算法的實質，也激發了學生自己歸納其他變換類型相關問題的濃厚興趣.考慮到課堂時間的有限性，把哈達瑪變換的快速算法流程圖作為作業，學生完成效果良好，這說明實例教學法在一定程度上能夠激發學生的自學能力.

第4個環節是指出離散哈爾變換的應用背景.根據圖像處理理論，矩陣中元素的排列位置是圖像信號特征的表示形式之一，引導學生如何應用離散哈爾變換找到這些特征，通過計算找到矩陣的具體特征形式，最后給出課前設計并通過MATLAB代碼實現的計算[10-11].

例2是典型的二維計算問題，應從4個關鍵點進行詳細分析和講解.

第1個關鍵點是將x分解為4個4×4的子矩陣.由于8階的哈爾矩陣形式復雜，0數據可看作圖像數據的邊界，易出現書寫和編程的錯誤，因此將x分解為4個4×4的子矩陣.用公式（6）計算是簡單易行的方法，在課堂上讓學生自主選擇8×8或者4×4的哈爾矩陣完成計算，發現選擇4×4形式的學生占多數，并且容易出現多種計算結果.

第2個關鍵點是通過編寫MATLAB代碼驗證學生計算的正確性.此時應將矩陣按照從左至右、自上而下分為4個4×4的子矩陣.

數值計算的MATLAB代碼：

第4個關鍵點是有效數字的選取.當符號計算的結果取5位有效數字時，與數值計算的結果相同.

通過分析和編程計算，使枯燥的二維哈爾變換計算躍然于屏幕上，極大地激發了學生的學習熱情.建議學生通過修改例2的代碼實現沃爾什變換和哈達瑪變換等計算問題，在一定程度上也提高了學生通過編程完成計算的實際能力，取得了較好的教學效果.

3 結論

本文在分析討論式教學法、問題式教學法和實例教學法基礎上，選擇實例教學法對離散正交變換理論教學過程的重要環節進行了歸納和總結，以哈爾變換為例詳細敘述了授課中所做的講解和分析.實踐表明，實例教學法是一種有效、可行的課堂教學方法，可以幫助學生快速精準地記憶變換公式，讓學生理解離散正交變換計算的關鍵所在，激發了學生自己歸納不同科目的數學理論，使之成為一個知識體系的濃厚興趣，也為學生在高年級學習專業課程打下了堅實的基礎，激發了學生的創新思維.

[1]王友國.大學數學課程體系和教學內容的改革與實踐[J].數學教育學報，2010，19（4）：88-91

[2]高凱，許云峰，張永強.電子信息類創新人才培養模式研究與實踐[J].教育教學論壇，2011（1）：232-232

[3]黃廷祝，高建.大學數學研究型教學方法和考試方法改革與實踐[J].中國大學教學，2012（11）：52-55

[4]楊春梅.關于討論式教學法及其應用問題探究[J].教育探索，2014（1）：62-63

[5]郭姣，劉艷良.問題式教學法在“信號與系統”課程教學中的運用[J].電氣電子教學學報，2010，32（5）：83-85

[6]余艷，邢遠秀，劉燕麗.關系數據庫范式理論的實例教學法探討[J].高師理科學刊，2016，36（2）：66-69

[7]胡茂林.矩陣計算與應用[M].北京：科學出版社，2008：268-305

[8]邱啟榮，張可銘.矩陣論與數值分析基礎[M].北京：中國電力出版社，2011：35-48

[9]李存金，張慧嬌.創新思維方法在大學課程教學中的運用[J].教育與教學研究，2013，27（9）：57-60

[10]王建衛，曲中水.MATLAB 7.X程序設計[M].北京：中國水利水電出版社，2007：67-185

[11]鄭連存，張艷.培養學生科學思維和創新能力的研究與實踐——談大學數學研究型教學[J].大學數學，2014，30（2）：43-47

Exploration and practice of the example teaching method of the discrete orthogonal transformation theory

WANG Jian-wei
（College of Mechanical and Electrical Engineering，Northeast Forest University，Harbin 150040，China）

In order to vividly explain the boring orthogonal transformation formulas，discusses the importance and concrete implementation methods of the example teaching about the discrete orthogonal transformation theory.The two typical teaching examples of discrete Haar transformation are designed in the teaching process.On the basis of inspiring the students to draw the flow chart of fast algorithm of the one-dimensional Haar transformation，the students respectively complete the calculation of the two-dimensional Haar transformation.It can make the students understand the key to the discrete orthogonal transform computation，helps the students understand the theory of the orthogonal transformation deeply.The practice has proved that the good teaching effects are obtained by the teaching method.

orthogonal transformation；discrete Haar transformation；example teaching

O151.21∶G642.0

A

10.3969/j.issn.1007-9831.2016.12.021

2016-09-22

王建衛（1973-），女，山東龍口人，副教授，博士，從事模式識別與智能系統研究.E-mail：jwwang2007@163.com

1007-9831（2016）12-0078-05