基于Runge-Kutta設(shè)計(jì)運(yùn)動(dòng)船舶數(shù)學(xué)模型*
江衍煊 黃 煥
(1.福建船政交通職業(yè)學(xué)院 福州 350007)
(2.福建交通職業(yè)技術(shù)學(xué)院航海技術(shù)研究所 福州 350007)(3.廣東海洋大學(xué) 湛江 524000)
?
基于Runge-Kutta設(shè)計(jì)運(yùn)動(dòng)船舶數(shù)學(xué)模型*
江衍煊1,2黃煥3
(1.福建船政交通職業(yè)學(xué)院福州350007)
(2.福建交通職業(yè)技術(shù)學(xué)院航海技術(shù)研究所福州350007)(3.廣東海洋大學(xué)湛江524000)
摘要為便于將海上船舶避碰問題利用計(jì)算機(jī)進(jìn)行研究,需要把船舶的運(yùn)動(dòng)特點(diǎn)用數(shù)字形式進(jìn)行模擬,把風(fēng)、流和浪等問題一起討論并尋找最合適的數(shù)學(xué)表達(dá)式模擬出船舶航行的狀態(tài),這樣才便于研究海上船舶避碰的問題。現(xiàn)以六面體船舶為典型特征來進(jìn)行研究,疊加了矢量風(fēng)、流和浪的數(shù)學(xué)表達(dá)式,并利用高階Runge-Kutta推導(dǎo)微分方程進(jìn)行高精度仿真船舶海上航行的特征,并建立相應(yīng)的數(shù)學(xué)模型以便于討論船舶避碰問題。
關(guān)鍵詞建模; 仿真; 六面體; 算法
Movement Ship Model Design Based on Ronge-kutta
JIANG Yanxuan1,2HUANG Huan3
(1. Fujian Chuanzheng Communications College, Fuzhou350007)
(2. Navigation Technology Research Institution, Fujian Chuangzheng Communications College, Fuzhou350007)
(3. Guangdong Ocean University, Zhanjiang524000)
AbstractIn order to facilitate the research for preventing collsions at sea, it can be studied via computers, which involves digital simulation of ship motion characteristics, considerations of wind, current and waves, as well as the layout of the most appropriate mathematical expressions to simulate the ship moving state. Based on the typical features of hexahedral ship, this paper researches superposing vector wind, current and waves, precisely simulating the characteristics of ship’s navigation at sea by high-order Runge-Kutta differential equation, establishing corresponding mathematical model, studies the prevention of ships’s collisions at sea.
Key Wordsmodeling, simulation, hexahedron, algorithm
Class NumberTP391.9
1引言
為了能夠利用計(jì)算機(jī)仿真船舶的航行狀態(tài),在考慮到船舶在水中的運(yùn)動(dòng)會受到多方面的影響下,目前把船體的運(yùn)動(dòng)狀態(tài)和受力考慮成六面體進(jìn)行研究[1],研究船舶所受到周圍各種作用的影響而建立相應(yīng)的數(shù)學(xué)模型并用微分方程表示。
2影響船體運(yùn)動(dòng)的因素
2.1水的作用
船舶航行會受到空氣和水的作用,水面下存在水的阻礙作用,主要由基本阻力、摩擦阻力以及興波阻力組成。基本阻力是靜水時(shí)對運(yùn)動(dòng)船體所產(chǎn)生的阻礙作用,摩擦阻力是船體對水運(yùn)動(dòng)時(shí),水的粘性所產(chǎn)生的阻力。興波阻力是船舶對水運(yùn)動(dòng)時(shí)產(chǎn)生船舶興波,該興波將沿著船體周圍所導(dǎo)致受到的壓力發(fā)生了變化而產(chǎn)生的阻礙作用。若船舶首尾線與流向存在交角時(shí),流速和靜水船速的合成速度將使船舶向水流來向相反一舷運(yùn)動(dòng)的效果[3]。
2.2風(fēng)的作用
船舶在航時(shí)水面以上部分將所受到風(fēng)的影響,若頂風(fēng)船舶就會減速,反之若順風(fēng)則船速會減速;風(fēng)向與首尾面斜交或者垂直則船舶受到風(fēng)的影響會朝著下風(fēng)漂移,船舶受到影響后船首將向上風(fēng)或下風(fēng)偏轉(zhuǎn)[11]。
3船舶數(shù)學(xué)建模
3.1模型的選取
研究船舶運(yùn)動(dòng)的核心內(nèi)容是為了船舶避碰,建立船舶的數(shù)學(xué)模型就是把復(fù)雜的船舶運(yùn)動(dòng)用數(shù)學(xué)公式進(jìn)行近似和簡化表達(dá),但也不能太過于簡單導(dǎo)致無法充分描述系統(tǒng)的主要性能,所以建立數(shù)學(xué)模型要盡量降低復(fù)雜度,同時(shí)盡可能提高精度。模型的設(shè)計(jì)必須包括風(fēng)、浪、流的干擾,且?guī)в蟹蔷€性的船舶數(shù)學(xué)模型,才能比較真實(shí)地模擬出船舶運(yùn)動(dòng)的實(shí)際狀況[1]。
設(shè)船舶的位置[x0y0]T引入六自由度的簡潔線性數(shù)學(xué)模型方程,則其狀態(tài)變量為:x(6)=[vrΔφδx0y0],速度平衡方程:
(1)
其中r為預(yù)設(shè)航向,Δφ為航向偏差,δ為輸入舵角。因風(fēng)浪對船舶漂移速度v及船首轉(zhuǎn)向角速度r影響以及海浪對船舶位置的改變,若流為恒速,那就會直接影響船舶位置和速度的變化,而不會影響航向,得到的速度平衡方程為[1]
其中:Vc為流速度,γc為流向。
3.2流的影響
用Norrbin簡潔的非線性表達(dá)非線性力、力矩的流體動(dòng)力表達(dá)式[2]:
其中,
式中C為橫流系數(shù),在自動(dòng)舵控制的閉環(huán)系統(tǒng)研究中應(yīng)用數(shù)學(xué)模型取值0.3~0.8之間。
3.3風(fēng)力的干擾
式中Cγ(γR)、CN(γR)為風(fēng)力和風(fēng)力矩系數(shù),經(jīng)計(jì)算得出風(fēng)力系數(shù)如表1所示。

表1 風(fēng)力系數(shù)表(wind coefficient)
通過插值法查表求得CN(γR)的值,n為表中序號,由式n=floor(γR/10)進(jìn)行浮點(diǎn)數(shù)取整獲得當(dāng)前數(shù)的最大整數(shù)。ρA為空氣密度值,C為表中n對應(yīng)的風(fēng)力系數(shù)值,AL是人工輸入的船舶水線面上側(cè)投影面積,或者由船舶尺寸參數(shù)進(jìn)行估算,VR為相對風(fēng)速,VT為絕對風(fēng)速,γR為風(fēng)弦角。同樣通過插值法查表可求得CN(γR)的值。
uR=-VTcos(αWIND-φ)-u
vR=-VTsin(αWIND-φ)-v
其中αWIND,ψ變動(dòng)范圍為0~360°,γR變動(dòng)范圍為0~±180°,風(fēng)向相對從右舷來時(shí)γR>0。大氣湍流形成的脈動(dòng)風(fēng)可以看作類似白噪聲的形式,則該標(biāo)準(zhǔn)差與VT的平方成正比,如下式[6]:
3.4波浪的影響
任何一短時(shí)刻的波浪可以看成固定頻率、周期和波高的規(guī)則波,假設(shè)船舶是規(guī)則的六面體,得到波浪的計(jì)算式:
其中k代表波浪數(shù),T為周期,L為波長,ξ(t)表示波浪在坐標(biāo)系原點(diǎn)處的振蕩,s(t)為波浪面在原點(diǎn)出的斜率,這里的ξ是沿著波浪傳播的方向。
4仿真算法
研究船舶自動(dòng)避碰不僅需要研究避碰算法還需要研究船舶航行的數(shù)學(xué)模型,只有數(shù)學(xué)模型與船舶實(shí)際在航相一致才能充分利用計(jì)算機(jī)進(jìn)行仿真,以便研究船舶的避碰。將船舶運(yùn)動(dòng)的數(shù)學(xué)模型轉(zhuǎn)換成計(jì)算機(jī)編程模塊,所以在進(jìn)行編程之前必須將其數(shù)字化、離散化。在考慮編程之前,必須選擇合理恰當(dāng),并且算法簡單,最重要的是精度要高的策略[6]。
4.1船舶擬人智能避碰決策(PIDVCA)
PIDVCA是進(jìn)行自動(dòng)推理、定量計(jì)算、分析,避碰決策的智能化很強(qiáng),對復(fù)雜海況的避碰時(shí)增加了大量的選擇性,導(dǎo)致在決策查找能力方面必然需要處理巨大數(shù)據(jù)量,因此對計(jì)算機(jī)數(shù)據(jù)處理速度要求很高,這就降低避碰決策的時(shí)效性,導(dǎo)致對物標(biāo)判斷延誤造成決策失誤而帶來安全隱患。
4.2粒子群優(yōu)化算法(PSO)
PSO源于人工生命和進(jìn)化計(jì)算理論,算法用的參數(shù)較少、簡便易行、較快的收斂速度等優(yōu)點(diǎn),但是這種算法搜索精度低,收斂速度慢,時(shí)效差。
4.3神經(jīng)網(wǎng)絡(luò)避碰決策模型。
神經(jīng)網(wǎng)絡(luò)是通過學(xué)習(xí)專家的知識和經(jīng)驗(yàn)和調(diào)用網(wǎng)絡(luò)結(jié)點(diǎn)的權(quán)系數(shù),并利用數(shù)據(jù)庫中的專家推理機(jī)制,從而實(shí)現(xiàn)自動(dòng)避碰決策過程,這種算法需要大數(shù)據(jù)的專家推理進(jìn)行計(jì)算,時(shí)效性也比較低。
在避碰決策時(shí)必須有其無可替代的數(shù)學(xué)公式的準(zhǔn)確性,然而實(shí)際航海環(huán)境中不僅需要算法的數(shù)學(xué)準(zhǔn)確性更需要結(jié)合實(shí)際航海規(guī)則。不僅需要研究避碰算法還需要研究船舶航行的數(shù)學(xué)模型,只有數(shù)學(xué)模型與實(shí)際在航相一致才能充分利用計(jì)算機(jī)進(jìn)行仿真[7]。
4.4Runge-Kutta算法
為了盡可能模擬船舶的運(yùn)動(dòng)狀態(tài),考慮用龍格-庫塔方法進(jìn)行跟蹤船舶運(yùn)動(dòng),再運(yùn)用計(jì)算機(jī)進(jìn)行仿真,只要龍格-庫塔的階數(shù)足夠高,就可以最大限度地模擬出船舶的運(yùn)動(dòng)態(tài)勢。
龍格-庫塔(Runge-Kutta)方法簡稱R-K法,它是應(yīng)用于高精度單步跟蹤的一種算法。利用該算法時(shí)步長不能太大,否則會導(dǎo)致精度下降。單階的R-K公式的穩(wěn)定性和跟蹤的精度遠(yuǎn)不如高階的R-K公式,所以為了高精度跟蹤船舶的運(yùn)動(dòng)狀態(tài)需要實(shí)時(shí)的最優(yōu)三級二階R-K公式或四級三階R-K公式。獲取Runge-Kutta高階的方法:
例如,某函數(shù)y(x)在xi-1處的斜率作為y(x)在[xi-1,xi]上的平均斜率K即:
K=y′(xi-1)=f[xi-1,y(xi-1)]≈f(xi-1,yi-1)
此為一階Runge-Kutta式。函數(shù)式為:yi=yi-1+hf(xi-1,yi-1)。
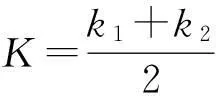
為了讓仿真的計(jì)算表達(dá)與真實(shí)運(yùn)動(dòng)的誤差盡量小,應(yīng)該使用高階Runge-Kutta方法,利用類似插值原理,在相應(yīng)的區(qū)間多取幾個(gè)點(diǎn),取相應(yīng)點(diǎn)斜率的加權(quán)平均值作為平均斜率。構(gòu)造3階或4階的R-K推斷公式就為了獲取更高精度。四階的公式為
為了提高精度的要求下,采用非線性數(shù)學(xué)模型,其離散化方法采用數(shù)值積分法,并采用四階的RUNGE-KUTTA方法建立的數(shù)值仿真模型。利用上式進(jìn)行推算得到船舶數(shù)學(xué)模型的四階表達(dá)式:
對于類似這種迭代方式的表達(dá)式,比較適合使用游標(biāo)進(jìn)行計(jì)算機(jī)計(jì)算。
begin
temp:=q;
q:=p;
p:=SPACE[q].next;
SPACE[Q].next:=temp;
Return()
End
利用相關(guān)計(jì)算機(jī)語言編程進(jìn)行迭代之后計(jì)算得到相關(guān)數(shù)值如表2所示。
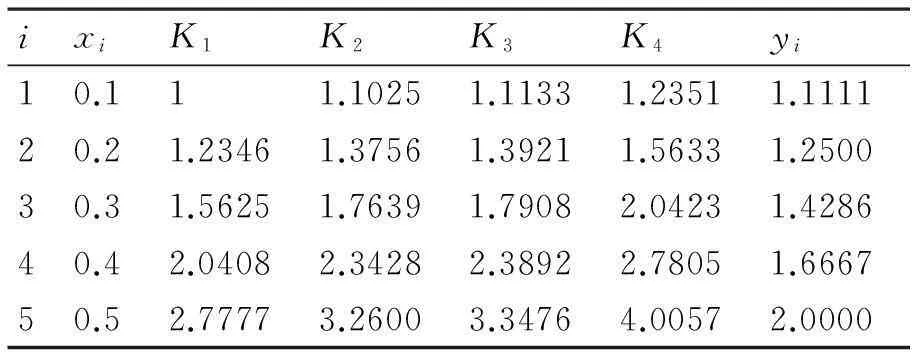
表2 計(jì)算出的相關(guān)數(shù)值
5數(shù)據(jù)模型表示
有了以上的表達(dá)式與計(jì)算機(jī)程序的計(jì)算結(jié)果之后,在設(shè)計(jì)船舶仿真時(shí)就需要添加對應(yīng)的風(fēng)流浪以及舵的作用,才能完整地體現(xiàn)出船舶運(yùn)動(dòng)狀態(tài)。
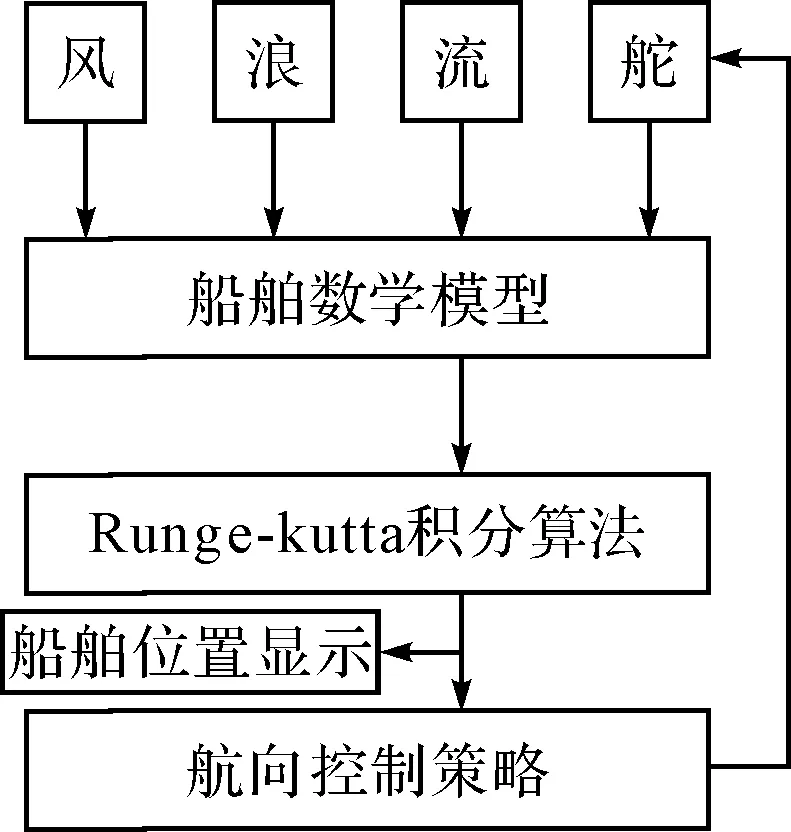
圖1 船舶運(yùn)動(dòng)參數(shù)疊加后情況
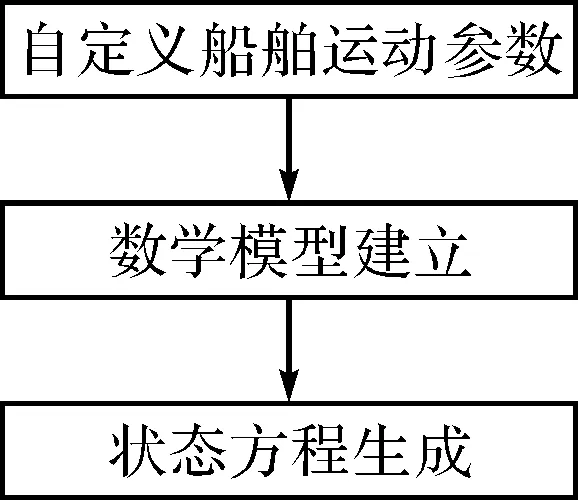
圖2 狀態(tài)方程設(shè)置
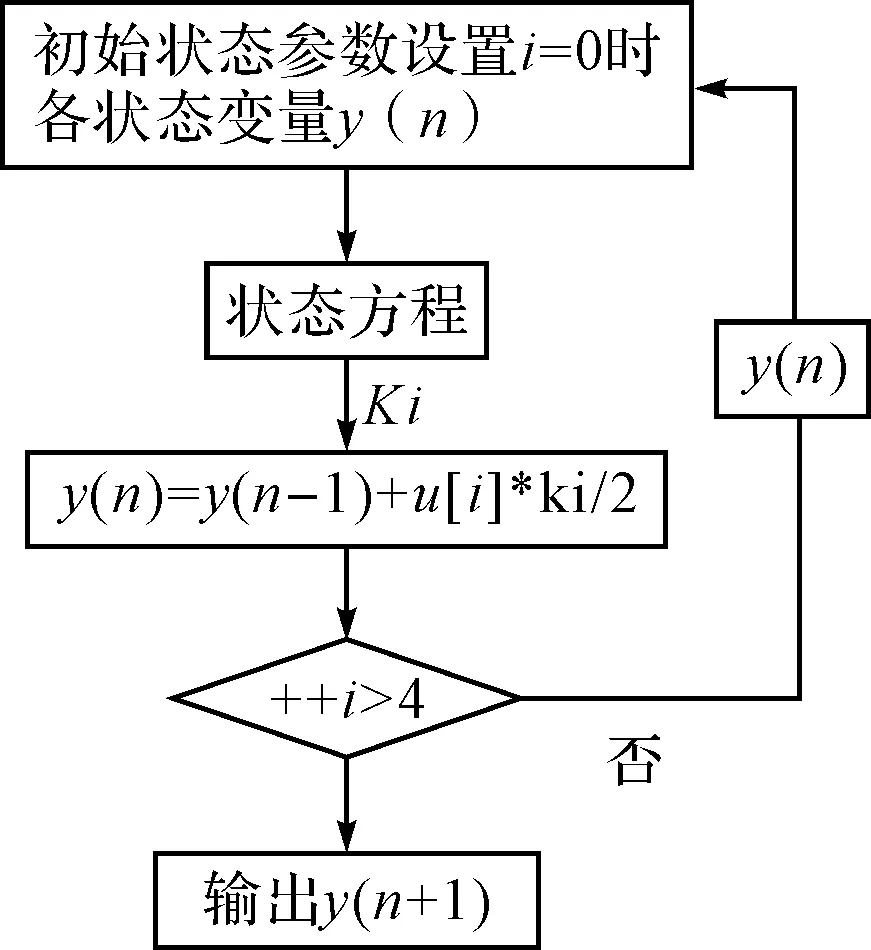
圖3 船舶模型的特征性
其中yn代表六自由度船舶模型中狀態(tài)初始量,yn+1代表仿真中期望得到的離散化結(jié)果,函數(shù)代表由數(shù)學(xué)建模之后由狀態(tài)空間模型方程計(jì)算出的微分方程,就是把船舶建模與Runge-kutta之間建立了聯(lián)系。如圖2所述在船舶部分初始化條件設(shè)置之后,就可以顯示出航向與位置,這樣船舶的運(yùn)動(dòng)狀態(tài)就基本可以確定了。
設(shè)計(jì)選取六自由度的船舶模型,考慮風(fēng)、浪以及流對船舶的影響為依據(jù)對船舶模型進(jìn)行了推導(dǎo),利用四階R-K方程可以高精度地接近船舶運(yùn)動(dòng)狀態(tài)的特點(diǎn)。
6結(jié)語
利用龍格-庫塔算法進(jìn)行仿真,在數(shù)學(xué)計(jì)算中誤差最小,利用計(jì)算機(jī)進(jìn)行仿真時(shí)計(jì)算量不大,速度比較快。這種模型在船舶仿真過程中,對于涉及多艘船舶互見的運(yùn)動(dòng)態(tài)勢,該方法在船舶間能夠更精確計(jì)算出相關(guān)的避碰數(shù)據(jù),有利于船舶及早采取行動(dòng)。
參 考 文 獻(xiàn)
[1] 孫宏放.船舶三自由度仿真平臺設(shè)計(jì)與預(yù)報(bào)方法研究[D].哈爾濱:哈爾濱工程大學(xué)碩士論文,2006:46-126.
[2] 王鳳軍.船舶避碰仿真平臺設(shè)計(jì)[D].大連:大連海事大學(xué),2013:66-89.
[3] 葉松,等.海浪干擾對船舶航向影響規(guī)律研究[J].艦船電子工程,2015(1):65-67.
[4] 史建,秀.船舶橫搖運(yùn)動(dòng)智能控制及其虛擬現(xiàn)實(shí)仿真研究[D].大連:大連海事大學(xué)碩士論文,2010:42-48.
[5] 汪宏,等.船舶失控撞擊高樁碼頭結(jié)構(gòu)的數(shù)值仿真分析[J].水運(yùn)工程,2015(6):51-55.
[6] 田超.風(fēng)浪流作用下船舶操縱運(yùn)動(dòng)的仿真計(jì)算[D].武漢:武漢理工大學(xué)碩士論文,2003:66-87.
[7] 吳立金,等.面向船舶軟件的仿真測試平臺研究[J].計(jì)算機(jī)測量與控制,2015(5):1451-1456.
[8] 邢道奇,龔銘.船舶航向模糊自適應(yīng)云模型控制[J].船舶,2015(3):42-47.
[9] 蔡新梅.基于UWB技術(shù)的船舶避碰系統(tǒng)抗干擾研究[J].艦船電子工程,2015(1):68-70.
[10] 殷虎,陳瑜.虛擬技術(shù)在船舶系統(tǒng)設(shè)計(jì)中的應(yīng)用研究[J].裝備制造技術(shù),2015(1):228-229.
[11] 田德,等.風(fēng)能與動(dòng)力工程專業(yè)教學(xué)理念研究與實(shí)踐[J].風(fēng)能,2015(1):44-45.
中圖分類號TP391.9
DOI:10.3969/j.issn.1672-9730.2016.02.023
作者簡介:江衍煊,男,碩士,副教授,研究方向:船舶通信導(dǎo)航與自動(dòng)化。黃煥,男,碩士,講師,研究方向:船舶通信導(dǎo)航及計(jì)算機(jī)在航海中的應(yīng)用。
基金項(xiàng)目:福建省教育廳科技項(xiàng)目(編號:JB08275,JB10226)資助。
*收稿日期:2015年8月14日,修回日期:2015年9月30日

