減振器復合閥片在彈簧作用下的變形解析計算

提　艷， 周長城， 趙雷雷， 潘禮軍

(山東理工大學 交通與車輛工程學院， 山東 淄博 255049)

?

減振器復合閥片在彈簧作用下的變形解析計算

提艷， 周長城， 趙雷雷， 潘禮軍

(山東理工大學 交通與車輛工程學院， 山東 淄博 255049)

摘要：復合閥片在彈簧作用下的變形一直是制約減振器優化設計的關鍵問題.根據閥片的力學模型，利用邊界約束條件和加載處的連續性條件，得到閥片彎曲變形微分方程通解，再通過恒等變換，建立了閥片在任意半徑處的變形解析式.通過實例解析計算與ANSYS仿真驗證可知，解析計算結果與仿真結果相對偏差僅為0.66%.結果表明，所建立復合閥片在彈簧作用下的彎曲變形解析計算方法是準確可靠的.

關鍵詞：筒式減振器； 復合閥片； 彎曲變形； 區段均布壓力； 解析計算

閥片在彈簧作用下的變形計算一直是制約減振器復合閥參數設計的關鍵問題，由于受邊界約束條件和變形連續性條件的制約，一直未能給出其精確的解析計算式.國外，對減振器閥片參數解析設計方面的研究很少，對彈性元件的復雜變形計算大多是利用有限元進行數值計算，也有學者利用能量法或攝動理論進行了近似計算，例如，文獻[1]利用FEA對復合金屬材料彈性變形進行了研究，但只給出了變形量的數值解；文獻[2]利用能量法對薄板彎曲變形進行了計算，但是計算過程復雜，無法給出簡潔的解析式.國內，已經有很多學者對減振器閥片變形計算進行了大量的研究，例如，文獻[3-4]曾對閥片在均布壓力下的變形以及非均布壓力下的變形進行了深入研究，并給出了簡潔的解析計算式，但是對于閥片在彈簧作用下的變形尚未給出精確的解析計算式.為了滿足減振器復合閥參數設計和特性仿真精確建模的要求，還必須解決復合閥片在彈簧作用下的變形解析計算問題.

本文根據復合閥片在螺旋彈簧作用下的力學模型，利用閥片變形微分方程及邊界約束條件和變形連續性條件，對復合閥片在彈簧環形集中力下的變形解析計算進行研究，并通過實例對復合閥片在彈簧作用下的變形進行解析計算和ANSYS仿真驗證.

1復合閥片在彈簧作用下的變形微分方程

1.1閥片在螺旋彈簧集中力作用下的力學模型

彈性復合閥片中間是固定約束，有效內圓半徑為ra，外圓半徑為rb，閥片厚度為h，螺旋彈簧半徑為rk，彈性系數為k，預壓縮量為x0的螺旋彈簧，作用在節流閥片上的總預緊力F0=kx0，如圖1所示.

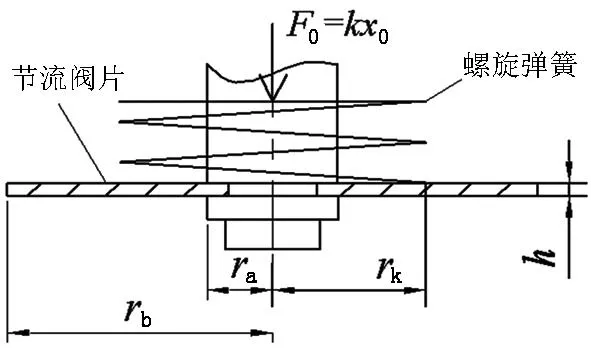
圖1　節流閥片在螺旋彈簧作用下模型

作用在復合閥片的環形集中力F0，可看作是作用在半徑rk處微環 [rk,rk+Δr] 上的均布壓力.因此，減振器復合閥片在彈簧作用下的力學模型可簡化為一環形集中力，如圖2所示.

圖2　節流閥片簡化力學模型

在復合閥片微圓環上的壓力p是繞z軸對稱，令rk+Δr=rt，因此，p可表示為

(1)

1.2復合閥片變形微分方程

由于復合閥片的結構和載荷都繞z軸對稱，根據彈性力學可以得到閥片變形曲面的微分方程[5-6]

(2)

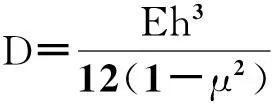
1.3復合閥片變形微分方程的解

微分方程(2)的通解為

(3)

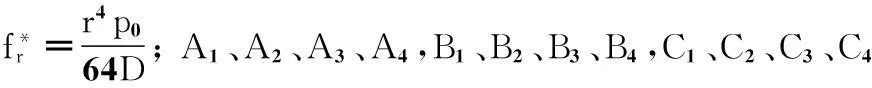
(1)內圓處的變形等于零，即fr1|r=ra=0，根據閥片變形曲面的通解式(3)，可得

(4)

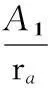
(5)

(3)外圓處的力矩等于零，即M|r=rb=0，可得

C32(μ+1)=0

(6)

(4)外圓處的剪切力等于零，即Q|r=rb=0，因此，可得

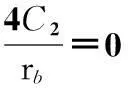
(7)

(5)閥片在半徑rk處的變形連續，即fr1|r=rk=fr2|r=rk，可得

(8)

(6)閥片半徑rk處的變形斜率相等，即

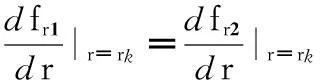
(9)

(7)閥片在半徑rk處的彎矩相等，M1|r=rk=M2|r=rk，可得

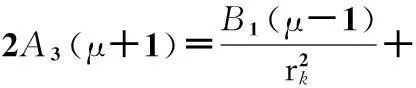
B2[2(μ+1)lnrk+μ+3]+

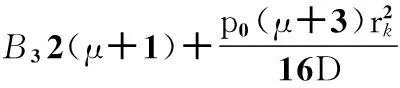
(10)

(8)閥片在半徑rk處的剪切力相等，即Q1|r=rk=Q2|r=rk，可得

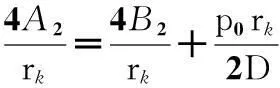
(11)

(9)閥片在半徑rk+Δr=rt處的變形連續，即fr2|r=rt=fr3|r=rt，可得

(12)

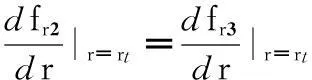
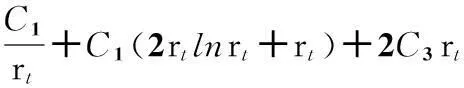
(13)

(11)閥片在半徑rk+Δr=rt處的彎矩相等，M2|r=rt=M3|r=rt，可得

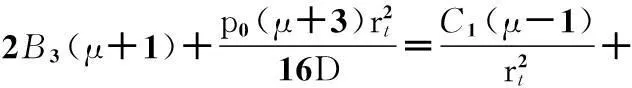
C2[2(μ+1)lnrt+μ+3]+2C3(μ+1)

(14)

(12) 閥片在半徑rk+Δr=rt處的剪切力相等，即Q2|r=rt=Q3|r=rt，因此，可得

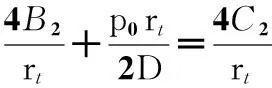
(15)

通過聯立(4)～(15)式，可求得復合閥片在區間均布環周壓力作用下的彎曲變形微分方程通解的12個常數，即A1、A2、A3、A4，B1、B2、B3、B4和C1、C2、C3、C4，從而得到在區間均布環周壓力下閥片彎曲變形通解表達式.

1.4復合閥片變形解析計算式

根據上述邊界約束條件和加載半徑r處連續性條件得到12個參數，將12個常數代入閥片變形曲面微分方程的通解表達式(3)，便可得到閥片在任意半徑處的變形解析式.通過分析可知，閥片變形解析式的各項都含有一個公因子p/h3，對式(3)提取公因子p/h3，將剩余項作為一個常數Gr，則復合閥片在彈簧作用下任意半徑r處的變形量可表達為[7-8]

(16)

式中，Gr為閥片在任意半徑r處的彎曲變形系數，單位為m6·N-1.

彎曲變形系數Gr與閥片結構、彈性模型、泊松比、預緊力加載位置rk和半徑位置r有關，例如，某環形節流閥片，閥片內半徑ra=5.0mm，外半徑rb=8.5mm，加載半徑rk=7mm，μ=0.3，E=200GPa.取預緊力F0(F0=20N)所作用的微圓環寬度Δr=0.1mm，即rt=7.1mm.則該節流閥片在此預緊力作用下的彎曲變形系數曲線如圖3所示.

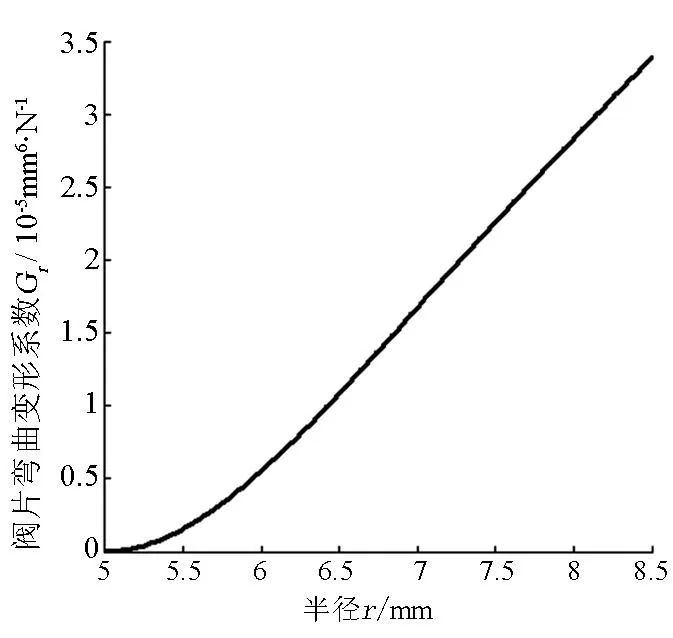
圖3　閥片變形系數隨半徑r變化曲線

2閥片變形解析計算實例

2.1復合閥片任意半徑位置變形

求得復合閥片在螺旋彈簧作用下任意半徑r處的彎曲變形系數后，據式(16)便可求得閥片在任意半徑r位置處的變形.例如，上述復合閥片，其厚度h=0.2mm，在半徑rk=7.0mm的圓周上施加作用力F=20N，則復合閥片的彎曲變形曲線如圖4所示.

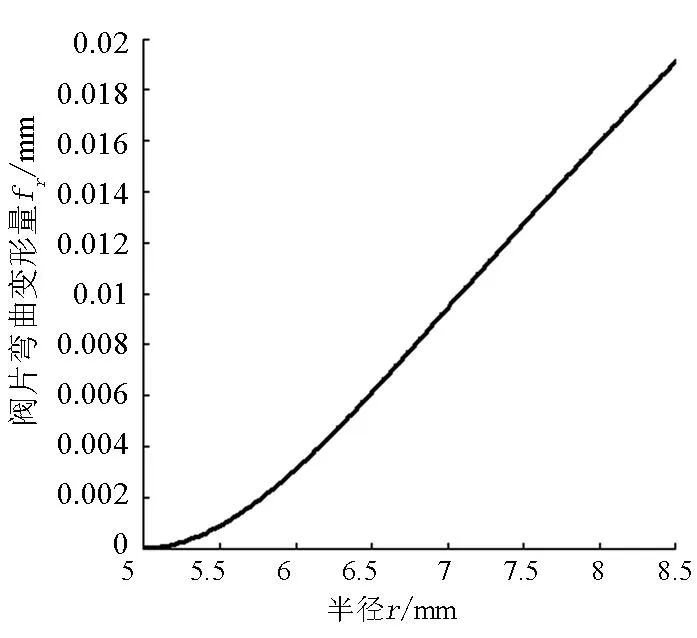
圖4　閥片變形隨半徑r變化曲線

2.2復合閥片在不同加載半徑位置下的變形

利用公式(3)，可計算復合閥片在不同區段均布壓力作用下任意半徑r處的變形.例如，復合閥片內半徑ra=5.0mm，外半徑rb=8.5mm，閥片的厚度h=0.2mm，μ=0.3，E=200GPa，分別在半徑rk=6.0mm,7.0mm和8.0mm施加環形集中力F=20N情況下，復合閥片在任意半徑處的彎曲變形情況如圖5所示.

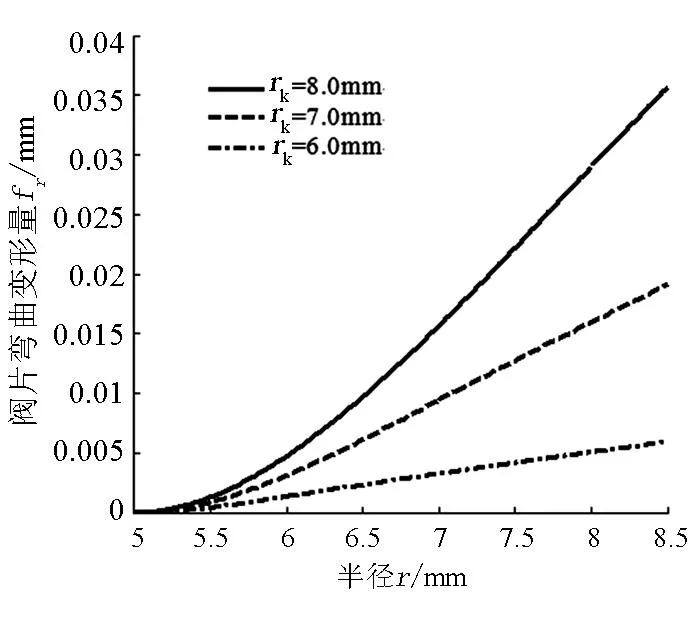
圖5　閥片在不同加載區段下的變形曲線

復合閥片在不同半徑上施加環形集中力的彎曲變形解析計算結果見表1.

表1在不同彈簧半徑下的閥片變形解析計算值mm

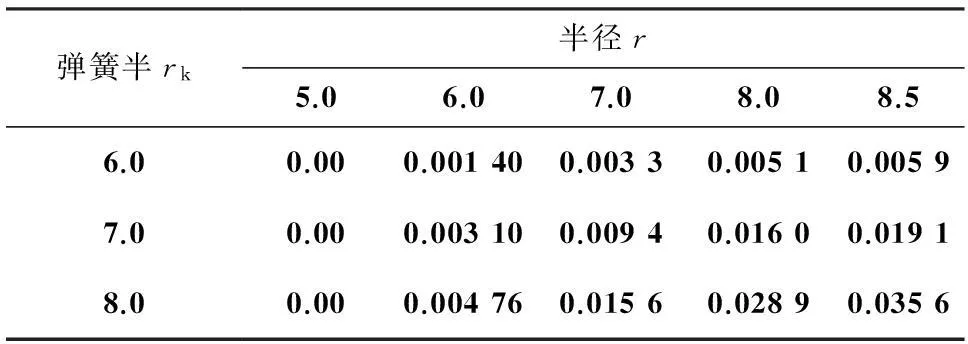
彈簧半rk半徑r5.06.07.08.08.56.00.000.001400.00330.00510.00597.00.000.003100.00940.01600.01918.00.000.004760.01560.02890.0356

由圖5和表1可知，相同復合閥片在不同半徑處加載相同的彈簧作用力，閥片的最大彎曲變形量隨著半徑的增加而增大；在復合閥片半徑rb=8.5mm處的彎曲變形分別為0.005 9mm、0.019 1mm、0.035 6mm.

2.3復合閥片在不同彈簧作用力下的變形

復合閥片在相同半徑處施加不同彈簧環形集中力，閥片的彎曲變形也會發生變化.例如，上述環形節流閥片，閥片厚度h=0.3mm，在半徑rk=7.0mm上，施加螺旋彈簧作用力分別為F0=50N，35N和17.5N的情況下，閥片變形的彎曲變形曲線如圖6所示.

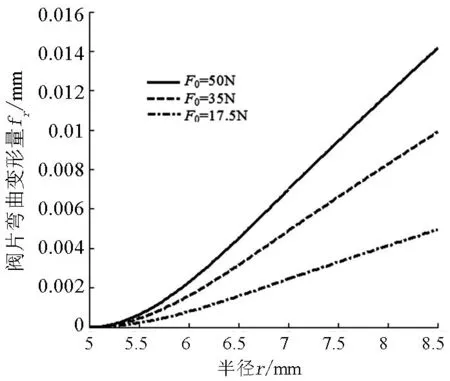
圖6　閥片在不同壓力下的變形曲線

復合閥片在施加不同環周力時不同半徑處的彎曲變形解析計算結果見表2.

表2在不同加載位置情況下變形fr解析計算值

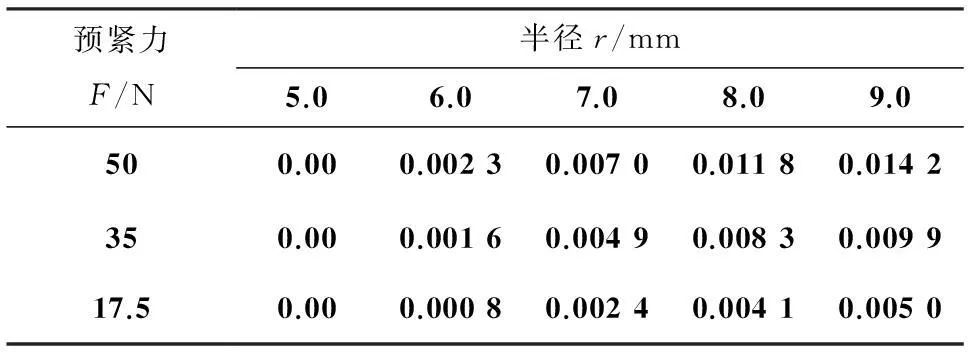
預緊力F/N半徑r/mm5.06.07.08.09.0500.000.00230.00700.01180.0142350.000.00160.00490.00830.009917.50.000.00080.00240.00410.0050

由圖6和表2可知，相同復合閥片在同一半徑處加載不同的環形集中力，閥片的彎曲變形隨著環形集中力的增加而增大；復合閥片在最大半徑rb=8.5 mm處的最大變形分別為0.0142mm、0.0099 mm和0.0050 mm.

3ANSYS軟件數值仿真驗證

對于上述節流閥片，利用ANSYS有限元分析軟件建立模型，以0.1mm為單位對模型劃分網格，在半徑r=[7.0,7.1]mm區間上施加均布壓力3.978 9MPa，即在該半徑區間上所施加的力F0=17.5N，對復合閥片進行彎曲學變形仿真分析，其仿真結果如圖7所示.

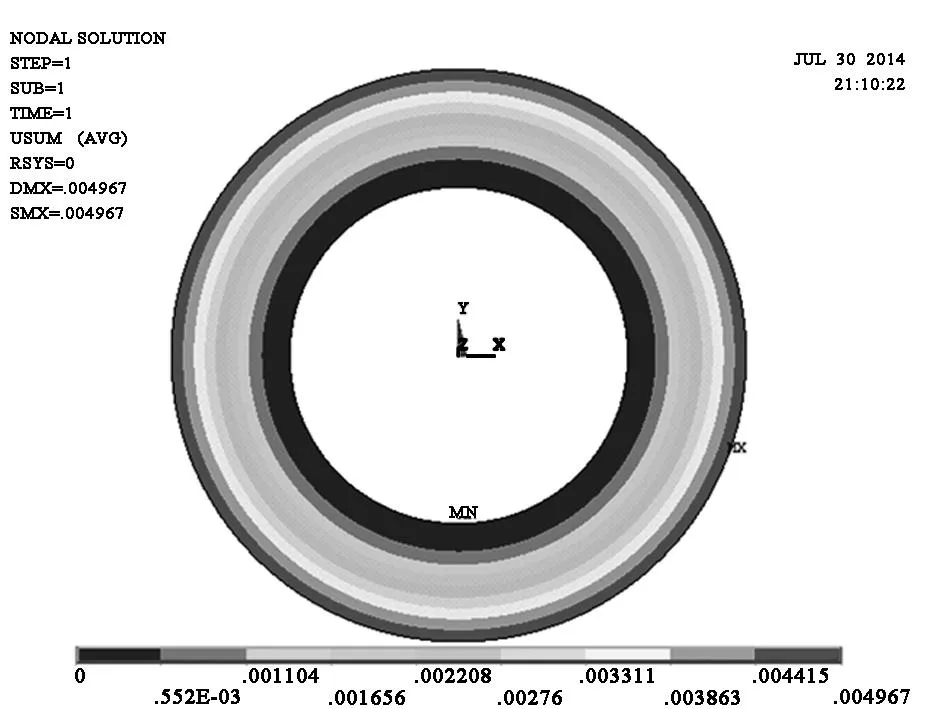
圖7　閥片變形仿真云圖

由圖7可知，利用ANSYS軟件對閥片在區段均布壓力下的彎曲變形進行仿真分析，所得到的閥片最大變形量為0.004 967mm，與上述解析計算得到的最大變形量相吻合，相對偏差僅為0.66%.結果表明，減振器復合閥片在螺旋彈簧作用下的變形解析計算方法是正確的.

4結論

通過對減振器復合閥片在彈簧作用力下的彎曲變形的理論分析、實例計算及仿真驗證，可知：

(1) 復合閥片受到的彈簧環周力可看作微環均布壓力，利用邊界約束條件和加載處的連續性條件，可得到復合閥片彎曲變形微分方程通解表達式.

(2) 復合閥片變形微分方程的通解表達式，經過數學變換，得到由彎曲變形系數與載荷和閥片厚度所組成的簡潔解析計算式，可實現復合閥片在彈簧作用下在任意半徑處的變形解析計算.

(3) 所建立的復合閥片在彈簧作用下在任意半徑r處的計算解析式， 為減振器復合閥參數設計提供了理論基礎.

(4) 利用彎曲變形系數計算得到復合閥片在彈簧作用下的變形，與ANSYS軟件仿真驗證值的相對偏差僅為0.66%，表明所建立的減振器復合閥片在螺旋彈簧作用下的變形解析計算方法是準確、可靠的.

參考文獻:

[1] Mihail A. FEA study on the elastic deformation process of a simple bimetal [J]. Applied Mechanics and Meterials, 2013, 371:448-452.

[2] Panthi S K, Ramakrishan N. Semi analytical modeling of springback in arc bending and effect of forming load [J]. Transactions of Nonferrous Metals Society ofChina, 2011, 21:2 276-2 284.

[3] 蔡艷輝,周長城.線性非均布壓力下減振器環形閥片變形解析計算[J].農業裝備與車輛工程,2009(10):24-27.

[4] 周長城,顧亮,王麗. 節流閥片彎曲變形與變形系數[J].北京理工大學學報,2006,26(7): 581-584.

[5] 徐芝綸. 彈性力學[M].北京:高等教育出版社,1990.

[6] 陸明萬,羅學富.彈性理論基礎[M].北京:清華大學出版社,1990.

[7] Zhou C C, Liu C C, Zhao L L. Deformation analytic computation of throttle of shock absorber [C]//Proceedings of the 2009 International Conference on Computational Intelligence and Natural Computing, 2009:359-361.

[8] Zhou C C,Mao S F, Zhao L L. Analytic superposition computation method of ring throttle slice deformation on non-uniform pressure [C]// 2010 IEEE International Conference on Automation and Logistics, 2010:193-196.

(編輯：郝秀清)

Analytic computation of compound slice deformation on spring-preload for telescopic shock absorber

TI Yan, ZHOU Chang-cheng, ZHAO Lei-lei， PAN Li-jun

(School of Transportation and Vehicle Engineering， Shandong University of Technology， Zibo 255049, China)

Abstract:Compound slice deformation on a spring-preload is a key problem of restricting shock absorber optimizing design. Based on mechanics model of compound slice, the differential equation solution of its deformation was got by boundary constraint and continuity condition of loading location, and analytic formula of its deformation was established with mathematical transform at different radius. With a practical example, compound slice deformation was computed and testified by ANSYS, relative deviation was only 0.66%. It′s shown that the computation method of compound slice deformation on spring-preload is accurate.

Key words:telescopic shock absorber； compound slices； bend deformation； section uniform load； analytic computation.

中圖分類號：U463

文獻標志碼：A

文章編號：1672-6197(2016)03-0001-05

作者簡介：提艷，女， tiyan0314@163.com; 通信作者： 周長城，男， greatwall@sdut.edu.cn

基金項目：國家自然科學基金項目(51575325)；山東省自然科學基金項目(ZR2013EEM007);山東省重點研發計劃項目(2015GGX105006)

收稿日期：2015-03-25