基于可拓方法的工程量清單招標模式下建筑工程項目不平衡報價識別

叢旭輝， 郭樹榮

(1. 山東理工大學 商學院， 山東 淄博 255012； 2.山東理工大學 建筑工程學院， 山東 淄博 255049)

?

基于可拓方法的工程量清單招標模式下建筑工程項目不平衡報價識別

叢旭輝1， 郭樹榮2

(1. 山東理工大學 商學院， 山東 淄博 255012； 2.山東理工大學 建筑工程學院， 山東 淄博 255049)

摘要：隨著工程量清單招標模式在建筑工程項目招投標中的應用，投標人常采用不平衡報價策略獲取高額利潤，致使業主遭受額外的經濟損失.針對建筑工程項目工程量清單投標報價特點，在可拓理論的基礎上，建立基于可拓方法的不平衡報價識別模型，首先計算各投標報價在不同衡量級別下的綜合關聯度值，然后借助優度值法對其不平衡度作出評判，最后運用綜合評分法直觀反映評判結果，為招標單位選擇最佳中標人提供決策依據.

關鍵詞：可拓； 建筑工程； 不平衡報價； 識別

工程量清單招投標模式廣泛應用于建筑工程、水利工程、園林工程等工程項目.《建設工程工程量清單計價規范》(GB50500—2013)規定：使用國有資金投資的建設工程承發包，必須采用工程量清單計價；非國有資金投資的建設工程，宜采用工程量清單計價.該招投標模式的特點之一就是招標人對工程量準確性和完備性負責，投標人則對分部分項工程的投標報價負責，且工程量清單僅供投標報價參考，這為投標人采用不平衡報價策略進行投標報價提供了機會[1].投標人常采取該策略，實現其“低價中標，高價結算”、獲取超額利潤的目的[2].招投標過程中，采用不平衡報價策略的投標人一旦中標，必然致使業主遭受一定的經濟損失.針對建筑工程工程量清單投標報價的特點，招標單位如何通過有效識別不平衡報價，為業主選擇最佳中標人提供決策依據，值得探索研究.

近年來，國內外專家學者分別對不平衡報價的產生原因及預防控制措施進行了研究，從增加額外收入方面分析其產生原因，從創新招投標模式[3]、提高施工招標設計圖紙質量和工程量清單編制質量[4]預防不平衡報價，從優化合同管理[5]和監管手段[6]控制不平衡報價的影響.上述研究成果可在一定程度上預防控制不平衡報價，但識別是制定預防和控制措施的基礎，如何在招投標階段有效識別不平衡報價引起了專家學者和政府相關部門的關注.專家學者主要借助數學方法對不平衡報價進行識別，其主要方法有:單純形法[7],其迭代過程較為復雜，實用性較差；收益最大化模型[8]，該模型在實際應用過程中所需邊界條件過多，較難實現其應用價值.政府部門主要通過制定規范性文件的方式識別不平衡報價，江蘇、云南、山東等省市依據有關的法律、法規與規章，結合本省市情況，制定了《工程量清單計價招標投標暫行規定》，多規定抽檢不少于十種項目的綜合單價進行分項目評審、評分，用以識別不平衡報價，其評價基點為平均價.該抽檢方法不能充分體現主要分部分項工程項目投標報價中總體分部分項工程投標報價的不平衡程度、變化態勢及對總價的影響程度大小.同時評價基點為平均價，若所有投標人投標報價均較高時，不能有效識別不平衡報價，易造成誤判.

為解決以上問題，提高不平衡報價識別的可靠性和實用性，本文借助可拓方法對建筑工程項目的不平衡報價進行識別，該方法通過關聯函數評判事物的特征量值在某一集合的隸屬度，實現對評價結果的定量描述，是一種識別事物特性的有效方法.本文建立了基于可拓方法的不平衡報價識別模型，首先計算各投標報價在不同衡量級別下的綜合關聯度值，然后借助優度值法對其不平衡度作出評判，最后運用綜合評分法直觀反映評判結果，為招標人選擇合適的中標人提供可靠的決策依據.

1基于可拓方法的不平衡報價識別模型

1.1物元分析模型

可拓學是由我國著名數學家蔡文教授于1983年創立，借助物元分析模型、可拓集合及其關聯函數，深入挖掘事物內部的特性和規律，認識、分析和解決現實世界矛盾與問題的方法[9].物元分模型是可拓方法的基本組成部分，包括事物N、特征值C和量值V，即R=(N,C,V)，通過數據分析和關聯函數，分析待評價對象各組成部分之間的矛盾性，借助物元變化實現矛盾問題與相容問題間的轉化，開拓出有關的決策策略集和關聯策略集，為管理者提供輔助決策[10].

不平衡報價識別指標具有亦此亦彼性和隨機性，且在不同的影響條件下具有可變性，具有不相容特性.可拓評價方法借助物元矩陣描述衡量條件，通過關聯函數實現對投標人投標報價不平衡性的定量評判，并運用關聯度值表征不平衡報價的特性.

1.2確定經典域、節域矩陣

1.2.1經典域矩陣

首先確定不平衡報價識別指標體系，然后構造其經典域矩陣

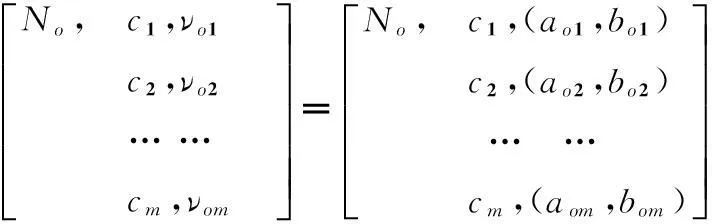
(1)

式中，No(o=1,2,…,n)表示所劃分的o個不平衡報價等級；ci(i=1,2,…,m)表示不平衡等級No的特征；νoi為不平衡等級No關于ci的量值范圍，即各不平衡等級關于各評級指標的量值區間，即經典域(aoi,boi)[11].

1.2.2節域矩陣

節域矩陣為

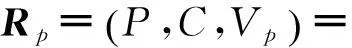
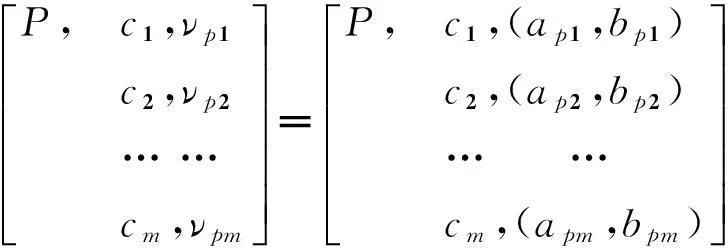
(2)

式中，P表示所有不平衡報價等級;Vpi為P關于指標ci的量值區間，即節域(api,bpi).

1.3確定待評矩陣

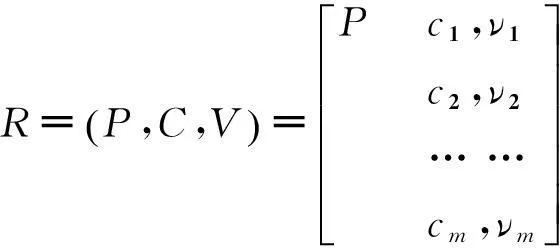
(3)

式中，P為不平衡報價的不平衡度;ci(i=1,2,…,m)是不平衡報價指標的特征因子；νi(i=1,2,…,m)為不平衡報價的不平衡性P關于特征指標ci的具體數值.

1.4確定關聯度及權系數

1.4.1關聯度

不平衡報價的不平衡性關聯函數定量地描述了不平衡性，給出不平衡性的可拓性.計算各不平衡報價指標的關聯函數值，即關聯度：

(4)

1.4.2權系數

根據各投標人投標報價數據，利用熵權法[12]客觀確定各不平衡報價評價指標權重系數ω=(ω1,ω2,ω3,…,ωm).

1.5綜合評判

由式(4)計算得到各指標對各不平衡等級的關聯度，由熵權法求得不平衡報價各評價指標的權值，將關聯度與權值代入公式，求得各不平衡等級下的綜合評判值：

(5)

經計算，求得各投標人投標報價對各不平衡等級的綜合評判值，取式(5)計算得到綜合評判值的優度值KO*=maxKo,{o=1,2…,n}，用以評判各投標人投標報價的不平衡級別.

1.6綜合評分法評價

為合理地表示投標人投標報價的不平衡性，直觀地表示評判結果，需按綜合不平衡度大小對其進行排序.首先對綜合評判值進行規范化處理，然后按不同的不平衡級別分別賦分，即令各不平衡級的分值為eo=(e1,e2,…,en)，求得不平衡度綜合評分，最后按照評分結果進行排序.

1.6.1綜合評判值的規范化處理

采用標準0-1變換方法對綜合評判值進行規范化處理，其中合理報價區間的數值屬性為效益型，其余區間為成本型.

(6)

(7)

r為投標人數，Kro為各投標人投標報價在不同級別下綜合評判值.

1.6.2不平衡度綜合評分

根據綜合評判值的規范化數據，結合各等級分值求得不平衡度綜合評分：

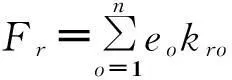
(8)

按不平衡度綜合評分對各個投標人進行排序，根據排序結果對不平衡報價進行識別，即Fr值越大，不平衡度越小，投標報價的越相對均衡；反之亦然.

2實例應用

某市某小區16#住宅樓項目采用公開招標的形式面向社會招標，該工程建筑面積為8327.91m2；結構形式為剪力墻結構；地上11層，地下2層；筏板基礎；其抗震設防烈度為7度；耐火等級為儲藏室一級，標準層二級；耐久年限為50年.

2.1評價指標體系與投標報價數據

本次招標共有4家企業通過資格審查，其審核結果顯示：該4家投標人的投標總價相差較小，難以辨識各投標人投標總價的合理性，但部分分部分項工程報價差異明顯，顯著存在不平衡報價行為.本文將影響工程造價的各主要分部分項工程作為不平衡報價評價指標，委托造價咨詢單位以社會平均先進水平為基準，編制主要工程量清單綜合單價分析表，并將該綜合單價作為不平衡報價評價基點.評價指標和投標人主要工程工程量清單報價見表1.

2.2不平衡等級與閾值

工程建造成本受施工工藝、材料價格變動等影響較大，致使各投標人對同一分部分項工程報價存在不同程度的差異.一般認為，分部分項工程投標報價浮動的合理區間為評價基點的±10%，較不平衡報價區間為±(10%～30%)，不平衡報價區間為±(30%～50%)，報價高于評價基點±50%屬惡意競標行為，應在招標文件中予以說明，若存在該種情況應予以拒標.本文以基準價為基礎，根據各分部分項工程報價浮動區間，確定5個不平衡報價等級，見表2.

在不平衡報價指標體系和不平衡等級的基礎上，構建不平衡報價識別的定量參照系用以衡量不平衡報價程度，即確定各指標于不同不平衡等級下的閾值區間.以指標1.1挖土方為例，其評價基點為21.05，與{低報價 較低報價 合理報價 較高報價 高報價}五個不平衡級別相對應的閾值區間為{[10.53,14.74) [14.74,18.95) [18.95,23.16] (23.16,27.37] (27.37,31.58]}.同理，可得各衡量指標閾值區間.

2.3指標權重確定

根據表1中各投標人投標報價數據，利用熵權法客觀確定各不平衡報價評價指標權重系數，其權重值見表1.

2.4綜合關聯度值計算及評判

利用式(4)可分別計算得不平衡報價各評價指標在各不平衡級別下的關聯度值，根據表1中的各指標權重值和式(5)求得各投標人投標報價在不同衡量級別下的綜合關聯度值，依據優度值公式Ko*=maxKo,{o=1,2…,n}取得其不平衡報價評判結果，其結果見表3.

表2不平衡報價等級劃分

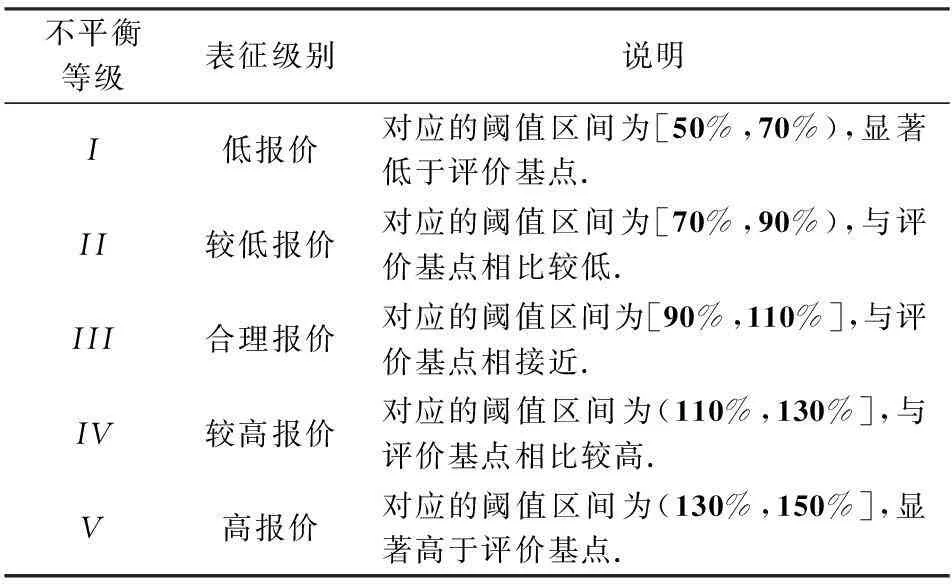
不平衡等級表征級別說明I低報價對應的閾值區間為[50%,70%),顯著低于評價基點.II較低報價對應的閾值區間為[70%,90%),與評價基點相比較低.III合理報價對應的閾值區間為[90%,110%],與評價基點相接近.IV較高報價對應的閾值區間為(110%,130%],與評價基點相比較高.V高報價對應的閾值區間為(130%,150%],顯著高于評價基點.

注：閾值區間的確定以評價基點為基準.

表1　不平衡報價評價指標和主要工程工程量清單報價　元

表3各投標企業不平衡報價綜合評判結果與分析

投標單位不平衡級別低報價較低報價合理報價較高報價高報價(I)(II)(III)(IV)(V)不平衡等級 變化態勢綜合評分企業1-0.4703-0.25710.0155-0.0415-0.3454IIIIV4.861企業2-0.352-0.3636-0.3763-0.1624-6.31E+12IVIII3.916企業3-0.2135-0.0537-0.2403-0.6841-0.5212IIIII2.884企業4-0.4428-0.22710.085-0.1141-0.3798IIIIV5.238

根據各投標單位投標報價在不同不平衡區間的綜合關聯度值，求得各投標報價的優度值，可知企業1和4的評判級別為合理報價(III)級別，企業2為較高報價(IV)級別，企業3為較低報價(II)級別，其中，企業1和4投標報價相對均衡，企業4優于企業1，但均有向較高報價變動態勢，可知少數分部分項工程存在較高報價；企業2的評判級別為(IV)，其投標報價處于較高狀態，根據公式(4)對其各指標進行關聯度分析，結果顯示該投標報價多數分部分項工程單價明顯高于評價基點，因此該企業投標報價高于社會平均先進水平；企業3的優度值為α企業3(II)=-0.0537，其報價變動態勢為趨向低報價狀態，且在I和II區間的綜合關聯度值均最大，該企業的施工技術和管理水平可能較其他投標人較優，也可能存在不平衡報價行為，其關聯度分析結果顯示，該企業明顯降低裝飾裝修工程等后期工程的投標報價，提高混凝土工程、砌筑工程等前期工程報價，屬嚴重不平衡報價.

2.5綜合評分法評價

為合理地表示投標人投標報價的不平衡性，直觀表示評判結果，按綜合不平衡度大小對其進行排序.首先利用式(6)和(7)對綜合評判值進行規范化處理，其中合理報價區間的數值屬性為效益型，其余區間為成本型；然后，按不同的不平衡級別賦分，合理報價賦3分，較不均衡賦2分，不均衡賦1分，即各不平衡級的分值為eo=(e1,e2,…，en)=(1,2,3,2,1)；最后，根據綜合評判值的規范化數據，結合各等級分值求得各投標報價不平衡度綜合評分，其中分值越高則報價越均衡，結果見表2.

由表3綜合評分可知，F4>F1>F2>F3，企業4和1投標報價的不平衡度較小，兩者投標報價相對較為均衡，與社會平均先進水平最為接近，且企業4優于企業1；企業2和3不平衡度較大，明顯存在不平衡報價行為.由此可知，企業2和3使用不平衡報價策略，實現其“低價中標，高價結算”、獲取超額利潤的目的。因此，招標單位可在綜合考慮其他評標因素的基礎上，優先選擇企業4和1為中標單位，以避免遭受額外經濟損失。.

3結束語

本文建立了基于可拓的不平衡報價識別模型，在評標過程中，準確識別不平衡報價既有助于控制工程造價、維護業主利益，又能保證工程招投標的公平公正，還可促使施工企業管理水平和技術實力的提升.工程實例證明，該模型能較好地識別評判各投標報價的不平衡度，減小不平衡報價對工程造價的影響，為業主選擇最佳的中標人提供決策依據.

參考文獻：

[1]CattellDW,BowenPA,KakaAP.Reviewofunbalancedbiddingmodelsinconstruction[J].Journalofconstructionengineeringandmanagement, 2007,133(8):562-573.

[2] 宋志勇.不平衡報價的量化識別與博弈研究[J].西安建筑科技大學學報(自然科學版),2012,44(1):109-133.

[3] 宋吉榮,鐘勝.工程量清單報價下工程項目招投標的一種新模式[J].軟科學,2006,20(5):82-85.

[4] 沈中友.基于招標人視角下不平衡報價應對策略研究[J]. 煤炭工程,2014,46(1):146-148.

[5] 烏云娜, 郝越明.不平衡報價的量化分析及防范[J].建筑經濟,2007(7):62-64.

[6] 尹貽林,徐志超,邱艷.公共項目中承包商機會主義行為應對的演化博弈研究[J].土木工程學報,2014,47(6):138-144.

[7] 陳瑜, 陳金華,夏光明,等.工程量清單計價模式中不平衡報價模型研究[J].武漢理工大學學報,2006,27(12): 118-120.

[8] 張英,沈苾文.清單計價模式下不平衡報價模型的建立及應用[J]. 武漢理工大學學報,2008,30(5):112-116.

[9] 王科奇,鄒廣天.論可拓建筑設計創新的基核——創新元[J].四川建筑科學研究,2014,40(2):248-252.

[10] 劉曉君,趙琰,趙翠芹.舊城改造項目可持續建設可拓綜合評價[J].科技進步與對策,2013,30(23):73-77.

[11] 蔡文.物元模型及其應用[M].北京：科學技術文獻出版社,1994.

[12] 張星. 自然災害災情的熵權綜合評價模型[J].自然災害學報,2015(6):191-194.

(編輯:劉寶江)

Identify unbalanced bids of building engineering under bill of quantities bidding mode based on extension theory

CONG Xu-hui1, GUO Shu-rong2

(1. School of Business， Shandong University of Technology， Zibo 255012， China；2. School of Civil and Architectural Engineering， Shandong University of Technology， Zibo 255049， China)

Abstract:With the application of the bill bidding model projects, bidders often take policies of unbalanced bid to achieve high profit in tendering process, which can cause the owners to suffer additional losses. By using the theory of extension, we created an identification method of unbalanced bids based on extension model. First of all, we calculated comprehensive correlation value under different levels. Then, we used the method of priority values to judge the degree of unbalance. Finally, we showed the results directly by using comprehensive score method, and provide decision basis for bidding unit to select the best winning bidder.

Key words:extension theory; building engineering; unbalanced bidding; identification

中圖分類號：TU723.2

文獻標志碼：A

文章編號：1672-6197(2016)03-0015-05

作者簡介：叢旭輝，男，congxuhui@126.com； 通信作者：郭樹榮，女，zbshur@sina.com.

基金項目：國家自然科學基金項目(71272017)

收稿日期：2015-09-10