基本解法在三維涂層結構溫度場中的應用
公顏鵬, 周愛華, 張耀明
(山東理工大學 理學院, 山東 淄博 255049)
?
基本解法在三維涂層結構溫度場中的應用
公顏鵬, 周愛華, 張耀明
(山東理工大學 理學院, 山東 淄博 255049)
摘要:研究三維涂層結構溫度場問題的基本解法,給出求解此類問題的新途徑,同時也拓展了基本解法的應用范圍.對結構厚度小到1×10-10的涂層結構溫度場問題進行了研究,所取得的數值結果與精確解相當地吻合,表明基本解法是求解涂層結構溫度場問題的強有力工具,且方法簡單、易于程序設計.
關鍵詞:基本解法; 涂層結構; 溫度場
隨著現代材料科學技術的發展以及實際工程的需要,具有耐高溫、耐氧化、耐磨損、抗腐蝕等優良特性的涂層結構愈來愈引起人們的重視,其應用范圍已涉及汽車、航空、建筑、陶瓷、刀具制造等諸多領域[1-3].然而,一般涂層材料的厚度較薄,約在微米級甚至納米級,受其厚度尺寸的限制,涂層材料中物理量的數值分析一直是工程中的難點.有限元法是常用數值分析方法,采用有限元法計算時,為了避免畸形單元,必須按照結構的厚度劃分網格,這將導致百萬甚至幾百萬個離散單元,計算工作量劇增[4].邊界元法可有效地處理涂層問題[5-6],但需要處理復雜的幾乎奇異積分.
基本解法(MFS)是由Kupradze和Aleksidze[7]在1964年提出的,它具有精度高、收斂速度快、程序設計簡單、無需對區域和邊界劃分網格、無需計算奇異及幾乎奇異積分、適合處理復雜區域和高維問題等諸多優點,已廣泛應用于固體力學、流體力學及熱傳導等問題的求解,取得了很好的效果. 然而,基本解法在三維涂層結構問題中的應用至今仍鮮有報道. 本文研究三維涂層結構溫度場問題的基本解法,為該類問題的研究開辟新的途徑,拓展其應用領域.
1三維位勢問題的基本解法
本文假定Ω是R3中的一個有界區域,Γ=?Ω是其邊界. n=(n1,n2,n3)是區域Ω的邊界Γ在x點處的單位外法向量.在邊界外部選取N個源點yj,j=1,2,…,N,則計算點x處的位勢為


若在邊界Γ上選取M個配置點xi,i=1,2,…,M,則邊界配置點處的位勢和法向梯度可表示為
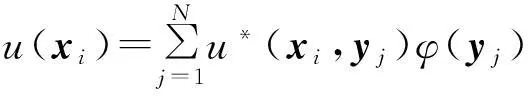
(1)
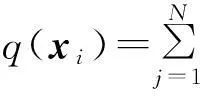
(2)
2三維涂層問題的基本解法
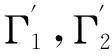

圖1 分域法結構圖


由方程(1)、(2), 在Ω1上可建立如下矩陣方程:

(3)
同理, 在Ω2上可建立如下矩陣方程:

(4)
對于適定的邊值問題,或者邊界上的溫度已知或者法向梯度已知. 邊界離散化后, 每個節點上都會產生一個代數方程, 方程的個數與虛邊界節點處待求密度函數的個數相同, 因而可以數值求解. 分域法將區域Ω1與Ω2看成兩個獨立的問題來處理, 在各自區域上利用虛邊界元法進行計算, 但在Ω1與Ω2的共同邊界ΓΙ上, 溫度與溫度梯度都是未知的, 因此未知參量的個數大于代數方程的個數. 要使得邊值問題可解,必須引入如協調條件:
(a)邊界ΓΙ上的溫度協調條件

(5)
(b)邊界ΓΙ上的熱流協調條件
(6)
若邊界Γ1,Γ2上節點的位勢已知, 根據條件(5)和(6), 式(3)和式(4)可合并成
(7)
若邊界Γ1,Γ2上節點的位勢梯度已知, 根據條件(5)和(6), 式(3)和(4)可合并成
(8)
類似地, 可寫出混合邊界條件相應的方程組.
式(7)或式(8)即為涂層結構溫度場虛邊界元法的基本列式. 通過式(7)或式(8), 可求出Ω1與Ω2虛邊界上的節點密度函數,進而可以利用內點積分方程求出內點的物理參量.
顯然,以上過程可以直接推廣到多涂層結構問題,只是聯立方程的個數有所增加,這里就不再過多闡述.
3數值算例
考慮2個涂層結構的數值算例來驗證本文方法的有效性. 為了表明方法數值解的準確性, 定義平均相對誤差

(9)

算例1研究球殼涂層結構的熱流問題. 圖中2(a)、2(b)是本文考察的空心球殼結構及網格模型. 圖3(b)是球殼涂層結構被x2x3平面切割的截面圖, 圖3給出了涂層結構及虛邊界計算模型被x2x3平面切割的截面圖. 基體是一內半徑為r1=1, 外半徑為r2=2的球殼, 涂層外徑為r3. 涂層厚度記為δ=r3-r2. 邊界條件如圖3(a)所示, 基體內表面溫度為10°C, 涂層外表面溫度為20°C. 基體導熱率為k1=1,涂層導熱率為k2=2.
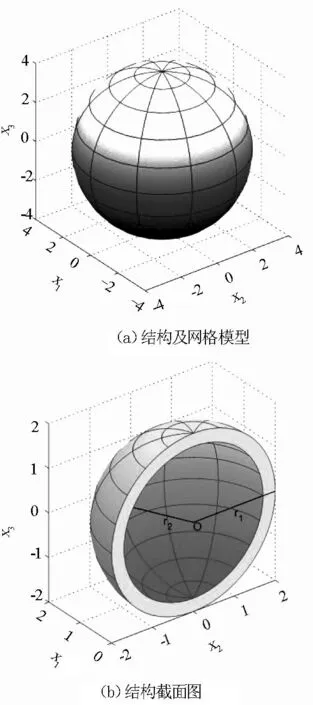
圖2 空心球殼結構
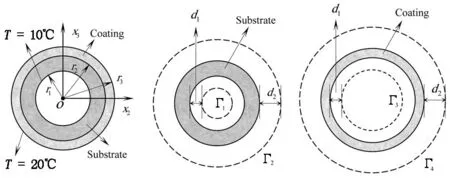
圖3 球殼涂層結構的熱流問題截面圖
定義涂層區域特征值最小尺寸與最大尺寸之比δ=(r3-r2)/r1為狹長比. 計算此模型時, 我們將每個虛邊界均劃分為64個單元, 總共256個單元. 為了更全面地反映方法的計算精度, 在基體與涂層接觸面上選取均勻分布的64個計算點, 并且虛實邊界距離設定為d1=0.4,d2=10. 圖4給出了不同狹長比下,即δ從10-1到10-10變化時, 涂層與基體接觸面上溫度與熱流量的平均相對誤差的變化曲線. 由圖4可以看出, 利用該方法計算的結果精度很高, 即使狹長比到10-10也能得到很理想的結果. 此外, 圖5(a)、5(b)給出了狹長比δ=1.0×10-7時, 接觸面上所取計算點的溫度解與熱流數值解的相對誤差曲面,可看出數值結果的相對誤差相當地小. 表明該方法非常有效.

圖4 接觸面溫度與熱流量數值解的平均相對誤差

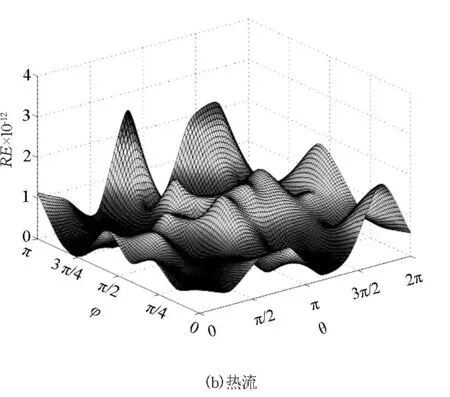
圖5 涂層與基體接觸面溫度與熱流解的相對誤差曲面
圖6給出了在狹長比與虛實邊界距離不變的情況下, 隨著單元數的增加, 基體與涂層接觸面上所取計算點處的溫度解、熱流解的平均相對誤差變化曲線即收斂曲線. 可以看出, 隨著單元數的增加,相對誤差迅速減小, 說明該方法具有良好的收斂性.

圖6 接觸面溫度解與熱流解的收斂曲線
算例2薄板涂層結構的熱傳導問題. 如圖7(a)所示, 基體長L=2, 高H=0.1, 涂層厚度為h. 已知基體下表面溫度為10°C, 涂層上表面溫度為20°C, 其余各側面熱流q=0. 基體導熱率為k1=1,涂層導熱率為k2=2.

圖7 薄板涂層結構圖
取虛邊界與結構外表面的幾何形狀相似. 圖7(b)給出基體結構及虛邊界計算模型, 圖7(c)給出涂層薄體結構及虛邊界計算模型. 基體虛實邊界間的距離與涂層虛實邊界間的距離已在圖7(b)與圖7(c)中標示. 基體上、下虛邊界以及涂層上、下虛邊界均劃分為64個單元,其余各側面虛邊界均劃分為8個單元, 共320個單元, 即本模型共有320個配點. 為了更全面地反映方法的計算精度, 在基體與涂層界面上及涂層上表面各選取均勻分布的400個計算點. 當涂層的厚度h從1×10-1變化到1×10-9時, 虛實邊界間的距離分別取d=2、 20、 40,圖8與圖9分別給出了界面上計算點處的溫度解和熱流解的平均相對誤差變化曲線. 可看出,d=20和d=40時,數值解的精度非常高,d=2時,解的精度較差,但精度仍可接受. 表明虛實邊界間的距離選取范圍非常地寬泛.

圖8 界面上溫度解的平均相對誤差

圖9 界面上熱流解的平均相對誤差
單元劃分情況不變, 取涂層厚度為10-9, 虛實邊界距離為d=10, 圖10(a)、10(b)分別給出了界面上所取400個計算點處的溫度解與熱流解的相對誤差曲面;可看出, 數值結果的相對誤差都非常地小. 表明該方法能夠準確高效地求解厚度小到納米級的涂層溫度場問題.

(a)溫度

(b)熱流圖10 涂層與基體接觸面溫度與熱流解的相對誤差曲面
另外,圖11給出了在節點數目相同的情況下,分別用邊界元(BEM)和基本解法(MFS)計算接觸面上溫度時平均相對誤差(ARE)隨涂層厚度的變化情況.容易看出,雖然兩種方法都能得到比較好的結果,但是本文解法(MFS)的精度比邊界元法高出好幾個數量級.表明本文方法在處理涂層問題時,比邊界元法在精度上有很大優勢.
4結束語
本文研究基本解法求解三維位勢涂層結構溫度場問題, 給出求解涂層結構溫度場問題的新途徑,拓展了基本解法的應用范圍. 數值算例表明, 基本解法是求解涂層結構溫度場問題的強有力工具, 即使結構的厚度小到10-10, 依然可獲得高精度的數值解.

圖11 涂層與基體接觸面溫度的平均相對誤差隨涂層厚度的變化情況
參考文獻:
[1]胡傳炘. 特種功能涂層[M]: 北京:北京工業大學出版社, 2009.
[2]楊曉光, 耿瑞, 熊昌炳. 航空發動機熱端部件隔熱陶瓷涂層應用研究[J]. 航空動力學報, 1997, 12(2): 183-188 .
[3]胡興軍. 刀具表面涂層技術進展綜述[J]. 產品與技術, 2008, 12(6): 91-94.
[4]LuoJF,LiuYJ,BergerEJ.Analysisoftwo-dimensionalthinstructures(frommicro-tonano-scales)usingtheboundaryelementmethod[J].ComputationalMechanics, 1998, 22(5): 404-412.
[5]張耀明, 谷 巖. 涂層結構中溫度場的邊界元解[J]. 固體力學學報, 2011, 32(2): 133-141.
[6]程長征, 牛忠榮, 周煥林,等. 涂層結構中溫度場的邊界元法分析[J]. 合肥工業大學學報(自然科學版), 2006, 29(3): 326-329.
[7]KupradzeVD,AlerksidzeMA.Themethodoffunctionalequationsfortheapproximatesolutionofcertainboundaryvalueproblems[J].USSRComputationalMathematicsandMathematicalPhysics, 1964, 4(4): 82-126.
(編輯:郝秀清)
Method of fundamental solutions of the temperature field in 3D coating structures
GONG Yan-peng, ZHOU Ai-hua, ZHANG Yao-ming
( School of Science, Shandong University of Technology, Zibo 255049, China)
Abstract:The method of fundamental solutions (MFS) for solving coating problems in 3D potential theory is developed, which not only provides a new approach to deal with such problems but also extends its application fields. Numerical examples demonstrate that the proposed method can effectively solve coating structure problems even when their thicknesses are as small as the nanometer scale, showing that the MFS is a simple and powerful tool for solving 3D coating problems.
Key words:MFS; coating structures; temperature field
中圖分類號:O342
文獻標志碼:A
文章編號:1672-6197(2016)02-0013-05
作者簡介:公顏鵬, 男, gyp2011@sina.com; 通信作者: 張耀明, 男, zymfc@163.com
基金項目:山東省自然科學基金重點項目(ZR2010AZ003)
收稿日期:2015-03-07

