解讀真題明方向 提升能力促解題——教材整合拓展對高三數學一輪復習解題教學的作用

楊松（杭州市余杭第二高級中學，浙江 杭州 311100）

?

解讀真題明方向 提升能力促解題——教材整合拓展對高三數學一輪復習解題教學的作用

楊松
（杭州市余杭第二高級中學，浙江 杭州 311100）

摘要：高中數學解題教學是數學課程教學的重要組成部分，特別是高三的一輪復習，解題教學更是體現了其重要性．高中數學教材是實現課程標準和實施課堂教學最重要的文本資源，也是高考命題和備考復習最直接的素材來源．“認真鉆研教材內容，正確理解教材意圖，準確把握教材要求——創造性地使用教材”是課改倡導的主要理念，同時也是一種操作策略。本文通過對2015年浙江省高考數學試題的解讀，簡要闡述了通過以教材整合為起點,落實雙基，理解通性通法，通過對教材的典型例習題進行深入挖掘優化學生思維，提高解題效率的一些思考和做法．希望借助本文引起各位高三一線教師在高三復習解題教學中關注教材的作用，培養學生的探究能力，提高學生思維發展的解題復習教學新模式。

關鍵詞：一輪復習；解題教學；整合拓展

“以問題為背景，以知識為主體，以方法為依托，以思維為主線.”這是2015年浙江省高考數學試題給我們的最大體會，也為2016年的高考復習指明了方向．高中數學解題教學是數學課程教學的重要組成部分，特別是高三的一輪復習，數學解題教學一直是教師和學生關注的焦點。

《普通高中數學課程標準（實驗）》強調：“數學課程要講邏輯推理，更要講道理，通過典型例子的分析和學生自主探究活動，使學生理解數學概念、結論逐步形成的過程，體會蘊含在其中的思想方法，追求數學發展的歷史足跡，把數學的學術形態轉化為學生易于接受的教育形態．”

高中數學教材是實現課程標準和實施課堂教學最重要的文本資源，也是高考命題和備考復習最直接的素材來源．“認真鉆研教材內容，正確理解教材意圖，準確把握教材要求——創造性地使用教材”是課改倡導的主要理念，同時也是一種操作策略。

因此在新形勢下的高三復習教學中，教師應充分認識課本資源例題所蘊含的價值，注重對課本資源的整合，探究一些典型題目中蘊含的東西，發揮其內在潛能，不僅能整合課本知識模塊，使學生深刻把握不同知識間的內在聯系，構建有序的網絡化知識體現，優化認知結構，而且有利于激發學生探究數學課本資源的熱情，開發學生思維的潛能，提高學生的數學素養，通過高三數學復習使學生的知識、技能和方法形成一個系統的、有機的整體，使學生的認知結構逐步完善，思維能力得到發展，心理素質不斷健全，不斷優化學生的數學思維，讓學生掌握更好、更快的解題方法，從而適應高考的需要．

下面從高考真題與課本資源之間的聯系為例，談談通過對課本資源的整合，構建知識系統，提高數學解題能力的重要性。

一、試題解讀，明確方向

表1　2015年浙江省數學高考理科試卷考查內容分布

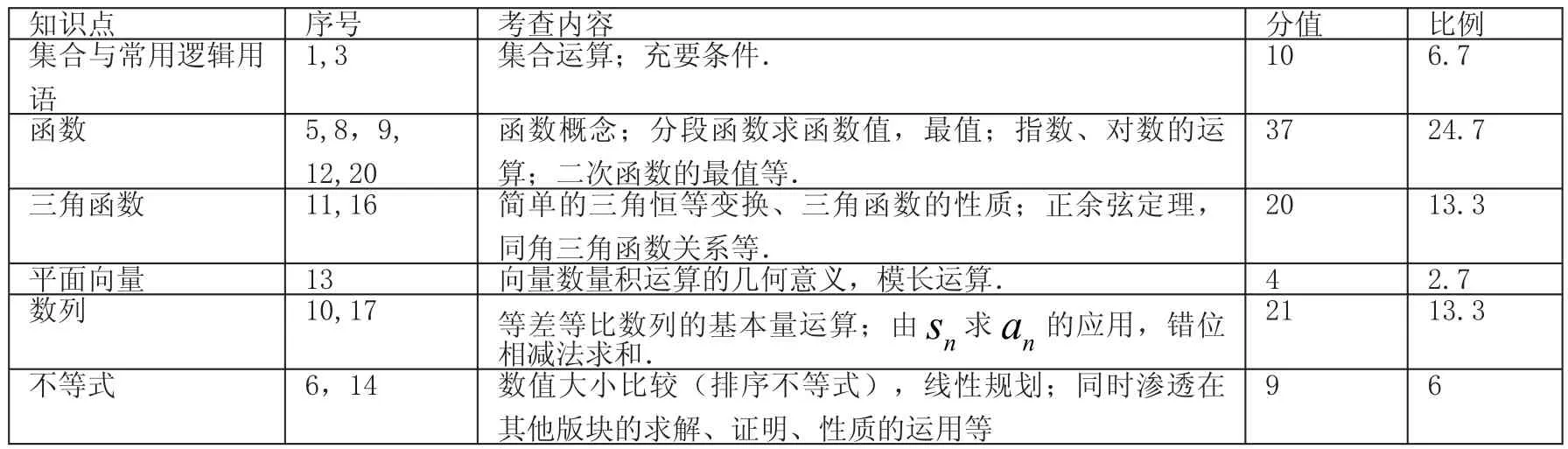
表2　2015年浙江省數學高考文科試卷考查內容分布

立體幾何　2,4, 18三視圖、體積計算；空間線面位置關系判定；直線與平面所成角的余弦值．25　16.7解析幾何　7,15,19　平面截圓錐形成圓錐曲線的方法；橢圓的性質，離心率求法；直線與圓的位置關系、直線與拋物線的位置關系，面積最值的求法．24　16合計　150 100

表3　2015年高考數學理科試題難度設計

表4　2015年高考數學文科試題難度設計

通過上述4張表格可以看出，2015年浙江省高考數學試卷全面考查了高中數學的基礎知識和基本技能，著重考查了中學數學教材中的主干知識，準確把握了高中數學的教學重點．試題覆蓋了高中數學的核心知識，涉及了函數的概念、單調性、周期性、最值、三角函數、數列、立體幾何、解析幾何等主要知識，考查全面而又深刻．同時將數學思想方法和素養作為考查的重點，提高了試題的層次和品位，特別是理科試卷能力考查步伐加大，許多試題保持了簡潔、樸素的特點，充分體現了數學語言的形式化與數學的意義，對考生的數學語言的閱讀、理解、轉化、表達能力提出了較高的要求。

從上述4張表格，還可以看出，雙基仍然是考查的重點，理科試卷基礎題46分，中檔題49分，文科基礎題52分，中檔題65分．其中基礎題主要是考查學生對概念的理解，題在書外，根在書中，起點較低，知識點相對單一．中檔題主要是考查學生的方法，題型熟悉，方法常規，考查主干知識，在知識交匯處命題．對于基礎題和中檔題主要是對基礎知識，基本技能的考查，讓不同層次的學生都能得到相應的分數，有的學生考試成績不理想，主要還是對基礎知識、基本方法掌握的不夠到位．在雙基上要舍得花功夫，強調雙基的重要性都不為過．創新題考查學生對本質的理解，意蘊深邃，不落俗套，盡可能地從數學模型、現實問題或幾何背景出發，構造出素材樸實、內涵豐富的試題，充分體現數學的內在實質．

由上述的分析，筆者認為高考數學一輪復習首先要重視考綱，及時做好2016年考綱與2015年考綱的對比，關注其中的變化．其次要注重數學概念的教學，在一定程度上“數學是玩概念，而不是玩技巧。”要回顧知識、落實雙基，幫助學生深刻理解數學概念．再次要注重數學思想方法，整合課本資源，梳理方法、構建系統，幫助學生更好的理解知識的交匯，掌握通性通法．第四要注重數學思維的提升，對課本的典型例習題進行探究拓展，優化思維，提升能力。

二、合理選擇，高效復習

（一）注重理解，夯實基礎，落實雙基解好基礎題。

《普通高中數學課程標準（實驗）》強調：“我國的數學教學具有重視基礎知識教學、基本技能訓練和能力培養的傳統，新世紀的高中數學課程應發揚這種傳統．”高三一輪復習，對高中數學學習的基本知識、基本方法、基本技能當然是不可或缺的．一輪復習不是簡單的重復，不能只一味追求速度，而是檢查自己在一些重要的結論，基本方法等知識點掌握上的錯誤和欠缺，進而能更有效地進行解題．在這一過程中，教材顯然是一輪復習的第一材料和抓手，只有注重理解數學概念，掌握基本技能，落實“雙基”，才能把基礎題扎扎實實的解好。

例如，浙江省2015年高考數學試題：

A.[0，1) B.(0，2]

C.( 1，2) D.[1，2]

A.[3，4) B.(2，3]

C.(－1，2) D.(－1，3]

分析：這兩個題目的“根”在課本，主要考查了二次不等式的解法，集合間的相互運算，連續實數的數軸輔助法，重點關注集合的端點是否能取的問題．

分析：這兩個題目的方法在課本，主要考查了等差數列的通項公式，求和以及等比中項的方程的應用，會根據題目的含義轉化為運算的方程。

筆者認為，植根教材的這些高考試題，知識背景公平，很好的起到了考查基礎知識和基本能力的要求．這些題目在課本的例題和習題中都有出現，且都具有典型性和代表性，在高三一輪復習的解題教學中，可以通過課本的例題和習題加深學生對概念的理解，對基本方法的認識，把“雙基”落實到位，學生只有理解數學概念，掌握基本方法和技能，才能解好這些基礎題，同時有了扎實的基礎，在復習過程中可以簡縮思維過程，提高解題的效率．

（二）回歸課本，理解通法，整合突破解好常規題。

浙江省的自主命題一直延續著新題不難，難題不怪的思路，重視雙基的考查，突出對主干知識、思想方法的考查，強調注意通解通法，淡化特殊的技巧。高三復習在落實雙基的同時，還需要幫助學生建構知識結構，溝通各部分內容之間的聯系，提高運用知識的能力．波利亞說過：“貨源充足和組織良好的知識倉庫是一個解題者的重要資本．”知識結構就是學生頭腦中的知識倉庫．在系統地掌握基礎知識和基本方法的同時，通知識網絡的建構，規范解題思路，形成通性通法。

（Ⅰ）求an與bn；

分析：本題第1問主要考查由sn求an，但在此基礎上有所改變，需要學生理解由sn求an的實質，能明確本題的左邊就是一個數列的和，得到遞推公式后再由累乘法求通項公式；第2問考查的使錯位相減法求和。

通過這個題我們可以看出，高考中檔題主要考查課本涉及的通性通法，這里運用了數列的兩個主干知識——數列通項，數列求和。三個核心方法——由sn求an，累乘法求通項，錯位相減法求和。

高三一輪復習，老師在解題教學時要注重學生對通性通法的理解，抓住過程中的易錯點，依托課本的例題，習題做好示范．如《人教社A版數學必修5》第44頁例3，在由sn求an的過程中要突出對n =1和n≥2的討論，在復習過程中可以配合對n =1和n≥2不能合成的情況，加深學生對這個方法的理解．第55頁，等比數列前n和公式的推導過程中讓學生理解錯位相減法的實質，再通過習題第61頁習題2.5A組第4題的3，深入理解錯位相減法，同時教師要做好板演示范，不能只注重知道這個方法，在演算過程中對易錯點要著重說明，比如

對應部分的項數，最后一項的符號這些都是易錯點，在課堂板演時要著重提示，引起學生的重視．這個題首項2也是可以并入到作差后的等比數列中，相應的運算就簡化了，在此基礎上可配合補充例題，如

（Ⅰ）求實數m的取值范圍；

分析：本題緊緊圍繞坐標法的核心思想，設計的問題是解析幾何中常規的弦長計算、垂直關系、求面積的最值，求解方法是解析幾何中的常規方法．學生在題目的解決過程中運算問題仍然比較大，有思想但運算不過關．

筆者認為，在高三復習解題教學需要回歸課本，重視通性通法應該成為我們的共識，進一步理解課本的例題、習題的思想方法，全面系統地掌握基礎知識和基本方法，規范解題思路，讓學生扎實掌握通性通法，同時課本的解題格式也為我們提供了解題的示范，復習資料中不規范的內容需要課本來正本清源．

在掌握通性通法的同時做好課本知識的整合工作，使知識與方法條理化、有序化、結構化，歸納總結各主干知識的問題特征、解題策略、易錯點，突出知識與策略間的聯系及適應范圍．在整合知識的基礎上通過找準難點、重點及薄弱環節進行有針對性的突破．在運算訓練上可以形成模塊化的訓練，如數列求和的運算模塊（公式法求和，分組求和，裂項相消法，錯位相減法等），解析幾何運算模塊（直線與曲線方程的聯立，弦長公式，面積球法，分式函數最值的求法等），這些模塊的運算訓練中較少的涉及解題思維問題，要求學生準確快速的運算，通過這樣的運算訓練學生在復習時才能解題效率，在高考時才會有更足的底氣。

（三）探究拓展，優化方法，提升思維解好創新題。

《普通高中數學課程標準（實驗）》強調：“學生的數學學習活動不應只限于接受、記憶、模仿和練習，高中數學課程還應提倡自主探索、動手實踐、合作交流、閱讀自學等學習數學的方式。這些方式有助于發揮學生學習的主動性，使學生的學習過程成為在教師引導下的‘再創造’過程。

高三一輪復習的解題教學要引導學生學會從不同角度思考問題，比較各種方法的優劣，從而開拓思路，優化思維．高一高二上新課時，由于受到教材章節的安排和知識能力的限制，課本上的例題一般只給出一種解法，這種解法著重體現當節內容的主要思想，能起到示范作用，高三的一輪復習學生獲得的知識已經比較系統，基礎也相對扎實，這時在一輪復習解題教學時可以引導學生從多角度思考，使知識網絡化，可以培養學生的解題思維。

課本絕大多數例、習題除了具有示范性、典型性外，更具有探究性，是課本的精髓，對它們進行轉化和拓展，呈現出豐富多彩的數學內容，往往成為高考試題推陳出新的源泉，有很高的教育價值。

絕對值的考查一直是浙江高考試題的一個熱點，對于含絕對值問題的處理主要是從代數與幾何兩個方向進行思考，代數法主要是看絕對值內的代數式的正負，再分類討論；幾何法主要是要理解絕對值的幾何意義——數軸上兩點間的距離；在高中學習過程中，對絕對值問題的最值求法還可以從絕對值三角不等式的放縮得到，絕對值三角不等式是《必修4》向量三角不等式的特例，可以看成是兩個共線的向量的模長間的關系，讓學生感覺“特技”的解法也能在課本中找到其原型，有利于學生對“特技”解法的理解，有助于學生能力的提升。

今年的理科第14,18題，文科第14題都給人留下了深刻的印象。它的解法可以從上述三種方法都能解決，如果我們在一輪復習解題教學中能按這樣的過程講解和分析，讓學生在整個遞進的過程中理解題目的實質，這樣對學生解題能力必定有較大的提升．

（Ⅱ）略．

分析：本題主要考查函數的單調性與最值、絕對值不等式的性質．題目的形式化程度高，但仔細考慮，第一問的單調性明確，最值只在端點處取得，情況沒有想象的那么復雜，同時第一問解法很多，不同層次的學生都能通過方法的選擇找到適合自己的方法．

解法1：

分類討論的方法看起來比較繁瑣，但在本質上分類討論思想是函數問題解決中的一個重要思想方法，是屬于“雙基”內容，也是學生應該掌握的基本解題方法．在分類討論去絕對值的同時我們還有辨別絕對值的“真假”，這樣可以簡化解題過程，例如

【2015浙江省高考數學文科14】已知實數x, y滿足2 21 x+ y≤，則的最大值是________.

這是兩個“假”絕對值，后續按線性規劃的方法可以直接解得答案．

筆者認為，分類討論是解決絕對值問題的一個通法，是建立在對絕對值符號內的代數式的正負的討論，是需要學生掌握的，同時在分類討論的意識下注重對絕對值的識別也是一個關鍵的步驟，在復習解題教學中，這樣的通法要重點落實，夯實學生的基礎，提高解題的效率．

解法2：

靈活運用絕對值的幾何意義，往往能使我們的解題過程直觀簡潔，這樣的解法在解法1分類討論之后更加顯得明朗，也體現了數形結合的思想方法在解題中的應用．同時絕對值幾何意義的考查在近幾年的高考題中也頻繁出現，當學生有這樣的幾何意識之后，解題時就會從幾何的角度來審視代數式的含義，使解法更加直觀簡潔。

A.5或8 B.-1或5

筆者認為，高三一輪復習解題教學不能只停留在解出題目的層面上，通過分類討論的通法解決過程我們嗅到了幾何的芬芳，這里結合幾何意義的求解過程顯然比分類討論要簡潔的多，這也是需要學生掌握的，但是學生在經歷了分類討論的解法后再來感受幾何意義就不會顯得突兀，這樣的解題教學學生的容易接受的，也必然是高效的．

解法3：

由前面的這個鋪墊學生就不難想到，對于數軸上的實數它的絕對值可以看成是以原點為起點的向量的模，因此對于實數a, b也可以有不等式：

這樣就得到了實數的三角不等式，這樣的探究拓展對學生的思維提升是有極大的幫助的，再由此得到

筆者認為，如果我們在復習解題教學中，對解題的理解有這樣深入的探究，那學生的思維能力必定會得到不斷的發展，同時也為學生的方法優化提供了依據，學生可以根據自己的理解去選擇適合自己的方法．高考作為選拔性的考試，在題目的設計上注重體現通性通法的同時，適當加入一些技巧元素，在高三復習解題教學中可以在落實通法的基礎上，適當補充對解法技巧的滲透．這樣的一輪復習解題教學模式應該成為重要模式，引領高三的復習教學．

總之，高三復習特別是解題復習教學的效果直接決定了學生的高考，這就需要每一位高三教師必須提高解題復習教學的有效性.作為高三復習教學的主導者，讓我們轉變觀念，通過一輪復習解題教學幫助學生從認識的角度熟悉課本，理解概念落實雙基解好基礎題，從理解的角度用活課本，理解通法，整合突破解好常規題，從掌握的角度拓展課本，深入鉆研教材中與高考命題的結合點，提升思維優化方法解好創新題．教師對高三復習解題教學做精心的設計，引導學生在理解概念，掌握通法中扎實基礎，感悟數學思想方法，在拓展中提升思維，增強解題能力，真正讓學生做到“通法”與“特技”齊飛，提高高三復習解題教學的有效性！

參考文獻：

[1]中華人民共和國教育部制定.普通高中數學課程標準（實驗）[M].北京：人民教育出版社。

[2]章建躍，主編.普通高中課程標準實驗教科書數學必修4[M].北京：人民教育出版社，2007。

[3]章建躍，主編.普通高中課程標準實驗教科書數學必修2[M].北京：人民教育出版社，2007。

[4]康小峰.教材起點 高考落點［J］.數學通訊,2015(1)：55-57。

[5]蔣明建.踐行課改精神 引領高效復習［J］.中學數學,2015(3)：28-30。

中圖分類號：G633.6

文獻標識碼：A

文章編號：1671-864X（2016）01-0283-05