概念定義靈活用 轉化運算促解題——高三解析幾何復習解題教學的幾點思考
楊靜(杭州余杭實驗中學,浙江 杭州 311100)
?
概念定義靈活用 轉化運算促解題——高三解析幾何復習解題教學的幾點思考
楊靜
(杭州余杭實驗中學,浙江 杭州 311100)
解析幾何教學是高中數學教學的重點內容,同時對學生來說也是難點所在,從高考中解析幾何的地位來看,其所占的分值也相對較大.從知識方面來看,高考命題常常立足于圓錐曲線的背景、定義以及問題解決過程中的幾何轉化等方面來設計;從能力方面來看,橢圓與雙曲線無論在概念、方程以及幾何性質上都具有較強的相似性,因此,其研究方式主要集中在類比遷移及差異分析等思維特質上,此外,對拋物線問題的考查,常常結合拋物線的定義及其幾何性質進行靈活轉化與應用,這些方面對學生而言都提出了較強的挑戰性.從考查的核心指向(體現學科特點)來看,高考中對解析幾何的考查必然結合了數形結合、化歸轉化等數學思想方法,同時結合了較為復雜的運算,對學生的數學思維和運算能力也提出了更高的要求。
作為高三復習解題教學,只有理解背景,立足定義,注重轉化,優化運算從這四個方面進行教學指導,才能讓學生學好解析幾何,提升解題的能力,同時教師的復習課堂也才能更有效。
一、理解背景,曲線類型明辨析
教材中對圓錐曲線的背景在章頭圖中有明確的探索與演示:“將兩個共點的圓錐放在一起,用平行于底面的平面去截,則得到的曲線是圓;將其稍作傾斜,得到的曲線是橢圓;若繼續傾斜,當截面與母線之一平行時,則得到拋物線;再繼續將平面轉起,則平面與上下兩個共點圓錐均相交,此時的曲線是雙曲線.這是圓錐曲線名稱的由來,其起源自古希臘數學家對于圓錐的研究得到的名稱,一直沿用至今.教材的“探索與發現”欄目中對圓錐的截口曲線為什么是橢圓更有進一步的推理與設問.
在高三復習教學中,對這一章的章頭圖及“探索與發現”欄目中內容有必要仔細分析,讓學生理解解析幾何的概念,會在概念的指導下在截面與圓錐的母線的關系中生成圓錐曲線.
結論:用一個不過圓錐面頂點的平面去截一個圓錐面,當平面圓錐的軸所成的角θ與圓錐母線與軸所成角α大小關系不同時,交線的不同情況如圖所示:
例1.(2015年浙江省高考數學文科第7題)如圖,斜線段AB與平面α所成的角為60°,B為斜足,平面上的動點P滿足∠PAB=30°,則點P的軌跡是( )
A.直線 B.拋物線 C.橢圓 D.雙曲線的一支
分析:解決本題的關鍵是要學生有立體幾何的模型——當動直線與定直線成角為定角時,動直線即為以定直線為軸的圓錐的母線,有了這個圓錐面的模型后再結合解析幾何的生成概念就不難得出答案了。
解:由AP與AB成定角為30°,可知AP是以AB為軸的α=30°的圓錐的母線,又AB與平面α成角為60°,即θ=60°可知α< θ <90°,因此交線為橢圓。
由此我們可以進一步得到:
當AB與平面α成角為θ=30°時,交線為拋物線;
當AB與平面α成角0≤θ< 30°時,交線為雙曲線.
在實際的教學中,解析幾何的復習往往更多關注的是解題的重復訓練和反復操作,這也在一定程度上體現了教師自身對這塊內容理解的不夠到位,把反復訓練當成是復習的全部顯然不利于學生對概念的理解和解題能力的提升,學生在遇到這樣的考題時只能是望而卻步。
筆者認為,在圓錐曲線的復習教學中,只有讓學生在動手操作中進行模型識別,在探究與推理中深刻理解圓錐曲線的背景,把對于圓錐曲線概念的背景、本質特征、內涵與外延的理解放在首位,才能切實幫助學生對圓錐曲線概念的同化,真正體會與梳理在問題解決過程中的方法,促進學生提升在問題解決過程中的思維和能力,實現認知圖式的擴張.
二、立足定義,數形結合促解題
解析幾何是在直角坐標系的背景下用代數方法研究幾何性質的典范,是數形結合思想的典型,但如果用純代數的方法進行研究,有時運算復雜,技巧較多,如果能利用圖形先作幾何量化的分析,數形結合的處理問題,能起到事半功倍的效果。
高三解析幾何復習解題教學必須立足圓錐曲線的定義,橢圓、雙曲線注重焦點三角形的靈活應用,拋物線關注焦點弦的基本性質等基本知識點,這些基本知識和基本性質是落實基礎的關鍵。
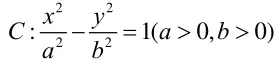
本例中用了兩次定義求得a,同時又對兩個焦點三角形的公共角應用余弦定理得到關于c的方程,從而求得c,進一步得到e,焦點三角形的仔細觀察及余弦定理的兩次應用是解決這個題目的關鍵。
筆者認為,高三的復習解題教學必須從基本定義及性質入手,善于觀察圖像的特點,用數形結合的思想引領解題,靈活應用定義,這樣才能夯實基礎,提升對此類題目的本質理解,有利于解題能力的提升。
三、注重轉化,思想方法齊滲透
在解決一些綜合性較強的解析幾何問題時,學生的困難往往是題目中的幾何條件不能準確地轉化為代數形式,導致問題無法解決。對于幾何條件的準確轉化其實質是數學思想方法的體現。
在高三復習解題教學中,數學思想方法的教學應逐步成為解析幾何重點與核心,因此,只有在解題復習教學中逐步滲透數學思想方法,對解析幾何問題結合化歸轉化,數學結合,方程函數等數學思想方法的教學,才能使學生對其理解透徹。
例3.(2015年浙江省高考數學理科第5題)如圖,設拋物線y2=4 x的焦點為F,不經過焦點的直線上有三個不同的點A,B,C,其中點A,B在拋物線上,點C在y軸上,則ΔBCF與ΔACF的面積之比( )
分析:解好本題的關鍵是降維和轉化的數學思想——把ΔBCF 與ΔACF的面積之比轉化為弦長BC與AC之比,再用拋物線的定義進行求解。
解:由A, B , C三點共線,及拋物線的定義
本題以直線與拋物線的位置關系為背景,考查轉化與化歸及數形結合的數學思想方法,題目表述十分簡潔,但對學生的轉化與化歸能力是又一定的要求的,這樣的解題如果沒有平時思想方法的不斷滲透,學生在解題過程中必然會碰到困難。
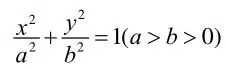
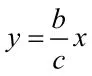
這是一道求橢圓離心率的題目,命題與浙江省的命題風格“條件簡潔、問題清楚”相一致,但考生普遍反映“入手容易,運算困難”,其實只要對題目的題意理解清楚,等價轉化到位,結合圓錐曲線的定義,題目的運算量是不大的,上述的這種解法,滲透了等價轉化,數形結合等數學思想方法,自然、流暢,計算簡潔。
筆者認為,在高三解析幾何復習教學中,只有不斷滲透數學思想方法,讓學生能準確理解題目的含義,靈活轉化題目的條件,再結合圓錐曲線的定義及相關基本性質,才能靈活解題,提高復習的效率。
四、優化運算,整合突破提能力
解析幾何的解題必然結合著較為復雜的運算,這也是學生感覺解析幾何問題解決較為困難的一個重要方面,但這樣的運算又無法回避,這就需要在平時多加以訓練.
在高三復習教學中,在運算訓練上可以形成模塊化的訓練,如直線與曲線方程的聯立,弦長公式,面積求法,分式函數最值的求法等.同時還要注重在運算過程中與其他知識的整合與銜接,如與函數結合的最值求法,與方程結合的韋達定理應用等,這些模塊的運算訓練中較少的涉及解題思維問題,要求學生準確快速的運算,通過這樣的運算訓練學生在復習時才能解題效率,在高考時才會有更足的底氣。
分析:本題的轉化是熟悉的,直接把弦長比轉化為坐標比,解好本題的關鍵在于運算,當“設而不求”運算有困難時,不妨“設而求之”。
這種解法的實質是消元的思想,直接把t轉化為了k的函數進一步求解。
解法3看似繁瑣,對于學生來說似乎更加自然,數據的處理也相對容易,但一般學生不會想到去嘗試,他不符合我們一般的解析幾何的解題經驗,在“設而不求”作為解析幾何運算中的重要方法的前提下,運用韋達定理運用有困難時不妨“設而求之”。
筆者認為,高三解析幾何復習解題教學的課堂,教師要舍得花時間讓學生去算,從而暴露學生的運算思維,教師也要舍得花時間進行板演,給學生作必要的運算示范,同時在運算過程中要注重整合,如分式函數的最值處理方法,方程韋達定理的靈活處理等,讓學生能在運算過程中去領悟這種思想方法,從而整合突破,做一個會一類,形成高效的復習.
總之,高三解析幾何的解題復習教學需要每一位高三教師必須提高解題復習教學的有效性.作為高三復習教學的主導者,讓我們轉變觀念,摒棄通過大量練習,使學生形成解題思維定式的復習方法.通過對解析幾何的理解背景,立足定義,注重轉化,優化運算四個方面入手,真正提升學生的解題能力。
參考文獻:
[1]謝舒.淺析解析幾何教學的三重境界[J].中學數學,2015(12):53-55。.
[2]李健.從條件轉化看解析幾何教學中思想方法的滲透[J].中學數學,2014(5):46-48。
中圖分類號:G633.63
文獻標識碼:A
文章編號:1671-864X(2016)01-0274-03

