地震信號時頻分析中的希爾伯特黃變換研究

周竹生， 羅勇濤

(中南大學　地球科學與信息物理學院，長沙 410083)

?

地震信號時頻分析中的希爾伯特黃變換研究

周竹生， 羅勇濤*

(中南大學地球科學與信息物理學院，長沙 410083)

摘要：隨著時頻分析方法的發展，生產研究上對復雜信號的時頻分析有了更高的要求。這里簡要介紹了希爾伯特—黃變換的原理和實現步驟，然后對合成信號進行經驗模態分解(EMD)和希爾伯特譜分析，進而將HHT方法運用到實際地震信號的時頻分析中。在此基礎上，運用經驗模態分解對合成地震信號進行了閥值去噪，證明了該去噪方法的有效性。

關鍵詞：希爾伯特—黃變換； 經驗模態分解； 地震信號； 時頻分析； 時頻濾波

0引言

在地震勘探中，由于地下介質的復雜性以及采集過程中的各種因素的干擾，獲得的地震信號具有非線性、非平穩等特征，是一種典型的非平穩隨機信號[1-2]。在以往的地震資料分析處理等研究中，傅立葉變換和功率譜估計都是基于平穩信號分析處理理論建立起來的，只能得到整個信號的頻率成分，不能同時得到信號的時間和頻率分辨率。短時傅立葉變換、小波變換和Cohen類等時頻分析方法，雖然可以得到信號在不同時間、不同頻率處的能量密度和強度，但由于這類方法還是基于傅立葉分析理論，因而也受到傅立葉分析不足的制約。1998年Norden. E. Huang等[3]發表了希爾伯特黃變換(Hilbert-Huang Transform，HHT)的相關論文。該方法主要分兩步：①自適應的經驗模態分解(Empirical Mode Decomposition，EMD)，得到有限個固有模態函數(Intrinsic Mode Function，IMF)；②進行希爾伯特變換，得到信號的瞬時頻率和振幅，進而得到希爾伯特譜。

地震信號作為一種復雜的非線性信號，其時頻分析方法自然也可以采用HHT方法，這里將HHT方法應用到實際地震信號的分析中，討論其應用效果。在此基礎上將經驗模態分解閥值去噪方法，運用到合成地震道集的去噪中，驗證了該去噪方法的有效性。

1HHT方法的原理

1.1經驗模態分解

在進行HHT方法的時頻分析之前，需要定義固有模態函數(IMF)。它必須滿足兩個方面的要求，①信號曲線過零點的數值和曲線的極值點數不能相差超過一個；②在任意一個局部范圍內，極大值的包絡線和極小值的包絡線是關于時間軸近似對稱的[3]。

經驗模態分解就是將原信號分解為有限個不同尺度的模態函數，具體流程是：

1)找出原始信號x(t)所有的極值點，并將其用三次樣條函數插值成為原數據序列的上包絡線bmax(t)和下包絡線bmin(t)，并求出其上包絡線和下包絡線的平均m1(t)。

(1)

2)將原數據序列減去平均包絡后，得到一個新的數據序列。

h1(t)=x(t)-m1(t)

(2)

判斷h1(t)是否為IMF函數，若不滿足IMF條件，將h1(t)看作新的x(t)，重復上述處理過程，直到h1(t)滿足條件時記c1(t)為IMF(1)：

c1(t)=h1(t)

(3)

然后令：

r(t)=x(t)-c1(t)

(4)

3)將看作新的x(t)，重復以上步驟1)和步驟2)，即可依次得到固有模態函數的各階分量IMF(k)，直到滿足給定的終止條件時篩選結束。終止條件為：

(5)

根據大量實踐表明，迭代閾值SD設為0.2～0.3比較合適[3]。

4)原始的數據序列即可由這些IMF分量以及一個均值或趨勢項r(t)表示。

(6)

也就是說分解得到的各分量可以通過簡單相加得到原信號，所以EMD分解得到的IMF分量都是原信號固有的模態特征。

1.2瞬時分量和希爾伯特時頻譜

將分解得到的每一階IMF分量進行希爾伯特變換：

(7)

式中cpv代表柯西主值( Cauchy Principal Value)。

構造解析信號:

(8)

于是得到幅值函數：

(9)

相位函數：

(10)

進一步可以求出瞬時頻率：

(11)

根據幅值函數和瞬時頻率，定義原始信號為：

(12)

這種將信號幅度表示在時間和頻率的平面上的分布就稱為Hilbert時頻譜，簡稱為Hilbert譜，用表示為：

(13)

式中ωj(t)=ω,Hilbert邊際譜的定義為：

(14)

邊際譜表示每個頻率在時間上的累計幅值，在統計意義上就是將所有的數據進行時間上的累加。

2EMD分解閥值去噪

常規的去噪方法(如F-K濾波、小波變換、廣義S變換等)，其理論都受傅立葉變換的限制，濾波效果都會受到濾波的通放帶的影響。希爾伯特-黃變換是以瞬時頻率為信號變化的基本量、特征模態為基本時域信號的一種新方法，不會像上述方法受傅立葉變換理論的約束，可以在全時段兼顧到頻率分辨率和時間分辨率，具有很好的局部特性和自適應性，適用于非平穩信號的濾波和去噪。

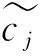
在實際運用中，通常閥值是固定的：

(15)

式中：σ2為噪聲的方差；N為采樣的長度。但是通常獲得精確的噪聲方差是很困難的，所以在計算中，常常采用估算的方法對噪聲方差進行計算。

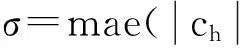
(16)

式中：mae表示平均絕對誤差；ch是IMF1的高頻系數。這是因為ch是分解得到的最精細的系數，主要就是噪聲系數。

3信號的EMD分解與時頻分析

3.1合成信號的EMD分解

參考文獻[6]中合成信號由一個調幅調頻信號和一個正弦波疊加而成，其中調幅調頻信號的基頻 為50 Hz，其調制頻率為20 Hz，正弦波的頻率為120 Hz。

圖1(a)所示為合成信號和分解得到的6階IMF時間域波形曲線。第一行表示原始合成信號；IMF1表示一階序列(c1(t))，是第一個分解出來的高頻信號，對應于原始信號中的120 Hz正弦波；IMF2表示一階序列(c2(t))，是第二個分解出來的信號，對應于原始信號中的50 Hz的調頻調幅信號；IMF3、IMF4、IMF5、IMF6和r6分別代表三階、四階、五階、六階序列(c3(t)、c4(t)、c5(t)、c6(t))和剩余殘量。根據EMD的分解原理，高頻信號應該首先被分解出來，即120 Hz的正弦波應該是IMF1;其次應該是50 Hz的調幅調頻信號，后面得到的IMF分量就是信號的趨勢分量和殘余信號了。這也證明了該方法的正確性和有效性。

3.2HHT時頻變換和常規時頻分析方法

對信號進行EMD分解后，將得到的所有IMF分量進行希爾伯特變換，再綜合各階瞬時頻譜，就得到信號的HHT時頻譜(圖2)。

從圖2(a)可看到兩條紅色曲線，分別代表了50 Hz為基頻的調幅調頻信號和120 Hz的正弦波。根據時頻譜圖可以看到，能量幅值隨時間和頻率是動態變化的，而且不同頻率的細微不同也能區分出來。圖2(b)所示為對應的HHT 邊際譜，它是不同頻率在整個信號時間內的能量積累。

圖3(a)和圖3(b)分別是短時傅立葉變換和平滑偽Wigner-Ville分布，可以看到，雖然這兩種方法都可以分辨出50Hz和120Hz，但不能刻畫出相應頻率的波形變化特征。這也正是由于這兩種方法都是基于傅立葉變換原理，不能進行局部的時頻分析。

根據上面合成信號的時頻分析，可以看到HHT方法相比傳統方法具有很好的優越性，它不需要人為選擇基函數，可以自適應地進行經驗模態分解，得到的固有模態函數是原信號的固有信息，而且可以根據需要改變幅值，從而能夠描述信號的非平穩程度。

3.3實測地震信號的EMD分解和時頻分析

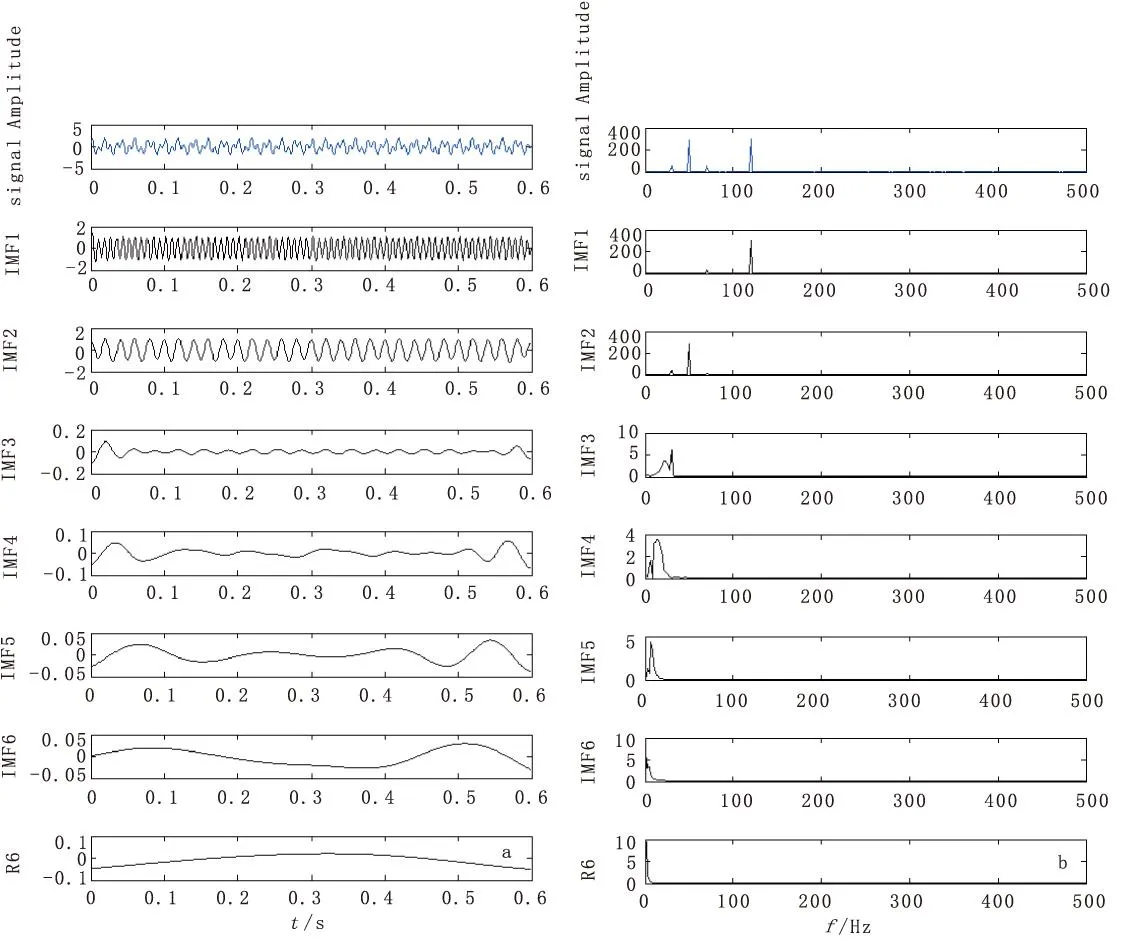
圖1　合成信號的EMD分解及其頻譜Fig．1　EMD decomposition and frequency spectrum of signal and IMF components(a)信號及6階IMF時間域波形；(b)信號及6階IMF的頻譜

圖2　合成信號的HHT時頻譜Fig．2　HHT time-frequency spectrum of signal(a) 合成信號的二維HHT時頻譜； (b) 合成信號的 HHT邊際譜

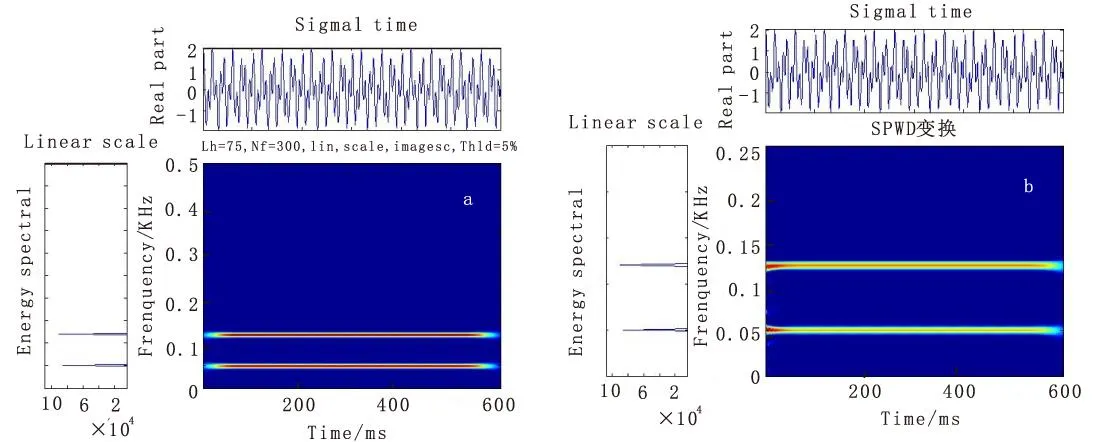
圖3　合成信號的時頻分析Fig．3　Time-frequency analysis of composite signal(a) 合成信號的短時傅立葉變換；(b) 合成信號的平滑偽Wigner-Ville分布

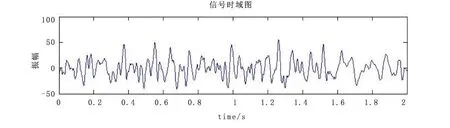
圖4　實測地震信號Fig．4　Original seismic signal

實際地震信號產生的復雜性以及采集過程中的各種干擾原因，地震檢波器獲得的信號往往是非線性、非平穩的。圖4是一個原始地震波形，采集時間間隔為0.001 s。通過HHT方法對該地震信號進行時頻分析，以說明HHT方法的有效性和刻畫信號非線性的能力。

圖 5(a)所示為實測地震信號及經過EMD分解后的8階固有模態函數(IMF)。由EMD的分解原理，可知各分量是按頻率從高到低排列的，其中高頻成分震動明顯，可以用于初動檢測；低頻分量可以看作是簡單的非線性變化，可以用來消除趨勢干擾和進行相關的校正。圖 5(b)所示為信號與各階IMF的頻譜，可見隨著分解次數的增加，得到的IMF分量能量也逐漸減弱。由圖5可見，整個記錄的能量主要集中在30 Hz以內的低頻成分，這是由于檢波器在地表附近，而震源在地下幾千米，經過地下介質的吸收衰減，只有低頻信號能被檢波器接收到。

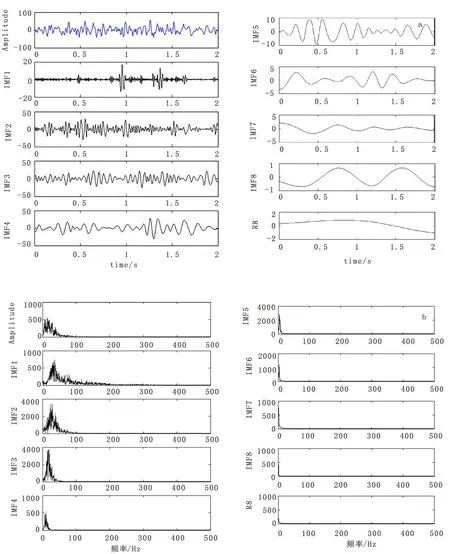
圖5　地震信號的EMD分解及其頻譜Fig．5　EMD decomposition and frequency spectrum of seismic signal and IMF components(a) 地震信號和8階IMF時間域波形；(b)地震信號和8階IMF的頻譜

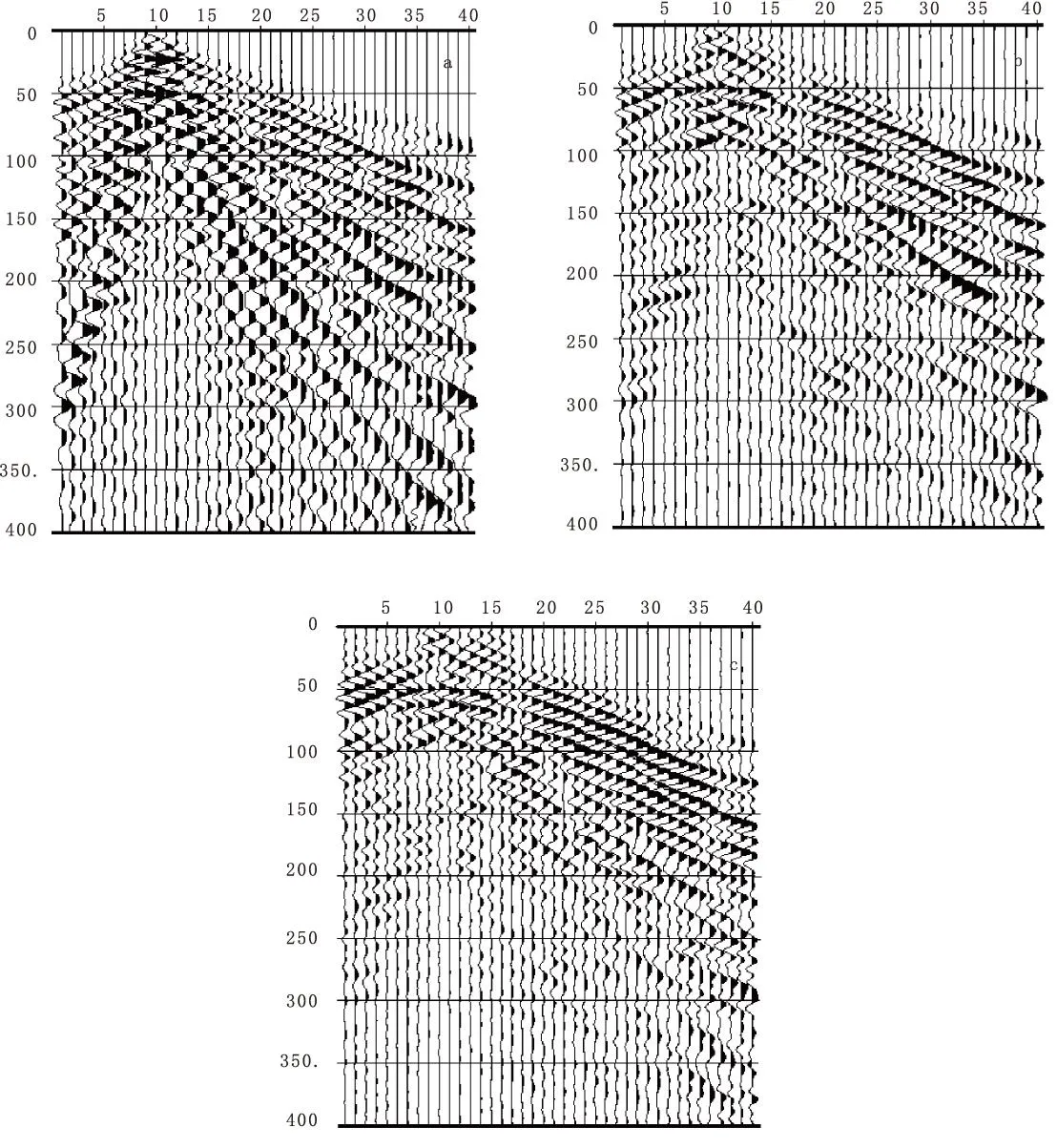
圖7　地震數據的去噪Fig．7　The seismic data denoising(a)原始單炮記錄；(b)F-K濾波結果；(c)EMD分解閥值去噪結果

圖6是對圖5(a)所示的所有IMF分量進行Hilbert變換得到的時頻譜。圖6(a)中的點、線表示能量變換特征的時頻演化過程，線表示能量的聚集性較好，且顏色越明顯，能量越大，反之，能量越小；點表示能量相對分散。由此可見，希爾伯特譜能很好地刻畫出信號幅值在時間和頻率上的變化情況，地震信號的非線性、非平穩特征都能很好的體現出來，在細微的變化上，能準確地表現出突變點的位置。圖6(b)為地震信號的HHT邊際譜，對應圖6(a)中每個頻率在信號持續時間內的能量積累，顯然能量集中在0 Hz～30 Hz頻段內，這與實際的采集情況是相吻合的。

由上述分析，說明HHT方法具有完全的自適應性，避免了人為選擇基函數和窗函數的影響，而且其時頻分辨率不受Heisenberg測不準原理的限制，具有完全的局部時頻分析能力[8-10]。

4EMD分解閥值去噪效果測試

在地震資料的去噪中，需要對每一道地震信號進行EMD分解閥值去噪，然后將處理后的地震道進行疊加輸出，就可以得到多道的單炮記錄或者疊加剖面。圖7(a)為實際的單炮記錄，可以看到地震信號受面波干擾嚴重，其反射波與面波混疊，反射波的同相軸分辨困難，地震信號的信噪比較低。

相較于F-K濾波，EMD閥值去噪不僅壓制了面波，加強了淺層信號的強度，使同相軸更加清晰，而且各個時頻段的能量均沒有大的損失，在單炮記錄上每一道數據均能很好地顯示。

5結論

1)運用EMD方法可以對信號進行自適應的分解，而且分解得到的每一個IMF分量都代表了原始信號的固有特征，因此可以選擇不同的IMF進行時頻分析，具有很好的靈活性。

2)HHT時頻譜在地震信號的時頻分析中，能夠反映地震信號隨時間和時頻動態變化的主要特征，且時頻分辨率不受Heisenberg測不準原理的限制，這為地震信號的識別、分析提供了有利條件。

3)HHT 時頻譜的能量主要集中在一定的時間和頻率范圍內，而不是整個時頻空間，這也真實反映了非線性、非平穩序列的本質特征。

4)HHT變換能夠很好地反映出信號的局部特性，也就能夠很好地反映出噪聲的頻率成分和范圍，因此運用經驗模態分解閥值能夠很好地對信號進行時頻濾波，去噪效果也比較理想。

[1]鄭治真，胡勁波.瞬時頻譜分析及其在地震趨勢估計中的應用[J].地震學報，1993，15(l)：68-75.

ZHENG Z Z，HU J B.Instaneous spectrum analysis and its application in estimation of earthquake tendency[J].Acta Seismologica Sinica,1993，15(l)：68-75.(In Chinese)

[2]劉希強，周蕙蘭，李 紅. 基于小波包變換的地震數據時頻分析方法[J].西北地震學報，2000，22( 2)：143-147.

LIU X Q，ZHOU H L，LI H.The time-frequency analysis method about seismic data based on wavelet packet transform[J].North-Western Seismological Journal,2000，22( 2)：143-147.(In Chinese)

[3]HUANG N E, SHEN Z, LONG S R, et al.The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc.R.Soc.London,1998,454:903-995

[4]WU Z，HUANG N E．A study of the characteristics of white noise using the empirical mode decomposition method[J]．Proceedings of the Royal Society A，2004，460(2046)：1597-1611．

[5]Wu Z H，HUANG N E．Ensemble empirical mode decomposition：a noise-assisted data analysis method[J]Advances in Adaptive Data Analysis,2009，1(1)：1-41．

[6]武安緒,吳培稚,蘭從欣,等.Hilbert-Huang 變換與地震信號的時頻分析研究[J].中國地震，2005，21(2)：207-215.

WU A X, WU P Z, LAN C X, et al. Hilbert-Huang transform and time—frequency analysis of seismic signal[J].Earthquake Research in China, 2005, 21(2): 207-216.(In Chinese)

[7]湯井田,蔡劍華,任政勇,等.Hilbert-Huang 變換與大地電磁信號的時頻分析研[J].中南大學學報，2009，40(5)：1399-1406.

TANG J T，CAI J H，REN Z Y，et al.Hilbert-Huang transform and time-frequency analysis of magnetotelluric signal[J].Journal of Central South University.2009，40(5)：1399-1406.(In Chinese)

[8]陳斌.時頻分析及在地震信號分析中的應用研究[D].成都：成都理工大學,2007.

CHENG B.Time-frequency analysis and its implication in seismic signal[D].Chengdu: Chengdu University of Technology,2007.(In Chinese)

[9]楊培杰,印興耀,張廣智.希爾伯特黃變換地震信號時頻分析與屬性提取[J].地球物理學進展,2007,22(5):1585-1590.

YANG P J，YIN X Y，ZHANG G Z.Seismic signal time-frequency analysis and attributes extraction based on HHT[J].Progress in geophysics,2007,22(5):1585-1590.(In Chinese)

[10]黃光南.希爾伯特黃變換及其在地震資料分析處理中的應用[D].青島：中國海洋大學,2009.

HUANG G N.Hilbert Huang transform and applications of it in seismic data analysis and processing[D].Qingdao: Ocean University of China,2009.(In Chinese)

Research on Hilbert Huang transform in time-frequency analysis of seismic signals

ZHOU Zhu-sheng， LUO Yong-tao*

(School of Geoscience and Info-Physics,Central South University,Changsha410083,China)

Abstract:With the development of time-frequency analysis, higher feasibility and accuracy on production has been required for complex signal. Firstly, the time-frequency analysis method of Hilbert-Huang transform and conception of transient frequency are introduced. The empirical mode decomposition and time?frequency distribution of a compound signal is carried on and then the actual seismic data were analyzed and processed based on Hilbert-Huang transform (HHT) spectrum. A time-frequency filtering method based on the transform is used by tasting on a synthetic seismic records example. The result proves its effectiveness.

Key words:Hilbert-Huang transform; empirical mode decomposition; seismic signals; time-frequency analysis； time-frequency filtering

中圖分類號：P 631.4

文獻標志碼：A

DOI：10.3969/j.issn.1001-1749.2016.01.09

文章編號：1001-1749(2016)01-0059-08

作者簡介：周竹生(1965-)，男，博士，教授，主要從事資源勘察、工程地球物理勘探、應用軟件研制及數據庫開發等方面的教學和研究工作，E-mail：672390136@qq.com。*通信作者：羅勇濤(1990-)，男，碩士，主要從事工程地震勘探的研究，E-mail：1206387954@qq.com。

收稿日期：2015-01-16改回日期：2015-04-13