改進的FCT方法在粘滯各向異性介質地震波模擬中的研究

李勤武， 周懷來

(成都理工大學 a.地球物理學院 b.油氣藏地質及開發工程國家重點實驗室

c.地球探測與信息技術教育部重點實驗室，成都　610059)

?

改進的FCT方法在粘滯各向異性介質地震波模擬中的研究

李勤武a,b,c， 周懷來a,b,c

(成都理工大學 a.地球物理學院 b.油氣藏地質及開發工程國家重點實驗室

c.地球探測與信息技術教育部重點實驗室，成都610059)

摘要：在地震勘探中，粘彈性各向異性介質相比彈性介質更能實際表征地下介質的性質，這里主要針對Kelvin模型從本構方程、幾何方程和運動微分方程，推導其一階應力速度方程，運用交錯網格有限差分法對其進行數值模擬，研究該介質中地震波的波場特征與傳播規律。同時分析了品質因子Q對地震波在振幅以及頻率上的衰減、吸收作用的影響。在數值模擬中，使用交錯網格算法必然會造成數值頻散或假頻現象，從而干擾數值模擬結果的正確性。為了提高數值模擬效果，對常規FCT(通量校正傳輸法)方法進行優化來壓制頻散，模擬實例證明，優化后的FCT方法要比常規FCT方法在消除頻散方面更加有效，能有效地改善數值模擬精度。

關鍵詞：Kelvin模型； 一階應力速度方程； 數值模擬； 品質因子Q； 優化后FCT方法

0引言

1845年Stocks第一次對粘彈性介質做了深入的研究，從那以后關于粘彈性介質理論和應用不斷發展。上世紀美國地球物理學家 N.H Rick[1]在Stokes 方程中引入地震結構子波理論，用統一完整的觀點將地震波在地層中衰減包含在理論中。目前出現了許多有關描述粘彈性介質的數學模型，主要包括 Kelvin-Voigt模型、Maxwell模型、標準線性模型等[2]。在這些模型中Kelvin-Voigt模型的性質更接近于固相介質，稱之為“固體型粘彈性介質”；而Maxwell模型其性質與流體相類似，也被稱為“流體型粘彈性介質”。在國內,張劍鋒等[3]在1994年對水平層狀介質中粘彈性波進行了數值模擬；畢玉英等[4]實現了二維粘彈性介質中的波場正演模擬；孟凡順等[5]通過有限差分算法對復雜地質體中的粘彈性波做了研究；杜啟振等[6]研究了裂縫性地層粘彈性介質的波動方程；牛濱華等[2]在出版的《半空間介質與地震波傳播》一書中詳細研究了彈性介質、粘彈性介質以及雙向介質中地震波的傳播規律；唐啟軍[7]實現了對Von Karman型隨機各向同性粘彈性單斜各向異性波動方程的數值模擬；賀同江等[8]將Forsyte廣義正交多項式微分算子與褶積算子相結合，實現了粘彈性介質的數值模擬。

為了壓制數值模擬中造成的數值頻散， Boris等[9]首次把流體動力學中通量校正傳輸法引入到地球物理中；楊頂輝等[10]將通量校正傳輸法應用到彈性波動方程正演模擬中；董良國等[11]對高階差分算法中各種因素對頻散的影響進行過理論探討；陳可洋[12]對通量校正傳輸法進行了改進。作者在Kelvin模型基礎上，運用優化后的FCT方法來壓制數值模擬中產生的頻散效應，應用效果證明了該方法有效性和正確性。

1方法原理

在粘彈性各向異性介質研究中，開爾芬(Kelvin)介質是人們在描述地震波衰減時普遍應用的一種介質模型，其衰減形式更接近于固相衰減。這里針對開爾芬(Kelvin)介質模型進行數值模擬，并運用優化后的FCT方法進行頻散壓制。

1.1一階應力速度方程

基于彈性力學理論，結合幾何方程、本構方程和運動微分方程可以推導粘彈性介質的一階應力速度方程。具體方程為式(1)。

(1)

其中：vx表示x方向速度；vy表示y方向速度；vz表示z方向速度；σxx表示x方向正應力；σyy表示y方向正應力；σzz表示z方向正應力；σxy表示xy方向切應力；σxz表示xz方向切應力；σyz表示yz方向切應力；ρ 表示介質密度。

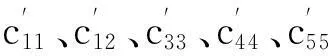
1.2一階應力速度方程離散化

在有限差分數值模擬中，相同的逼近階數情況下，交錯網格差分格式的精度大約是常規差分格式精度的4倍，通過提高逼近階數會相應地提高差分精度，但同時也會降低運算速度。當空間差分逼近階數提高到一定階數后再提高逼近階數，對精度的影響就不大了,因此在數值模擬時，需要兼顧計算速度和逼近精度。

對具有2N+1階導數的連續函數f(x)離散化，其2N階精度的交錯網格差分格式為[14-17]式(2)。

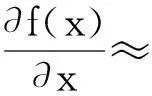
(2)

其中：x是變量；Δx是步長；ci是差分權系數；i=0,1,2…,N。式(3)是式(1)離散化后時間2 階空間2N階方程

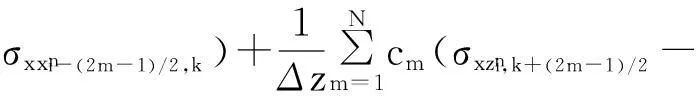
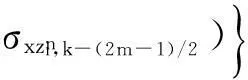
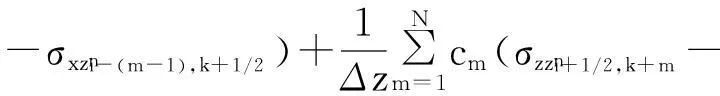
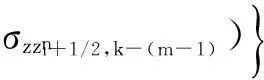
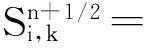
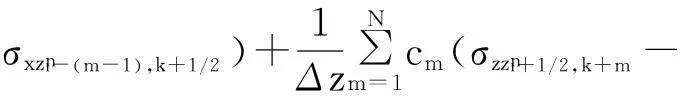
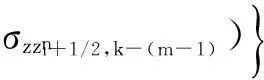
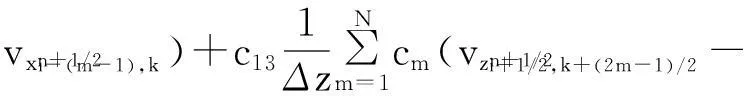
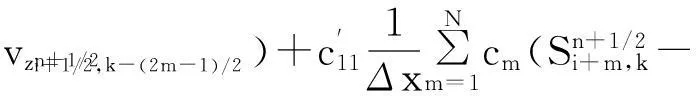
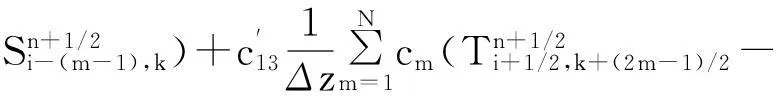
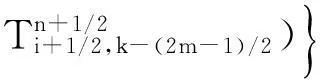
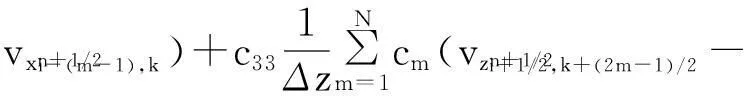
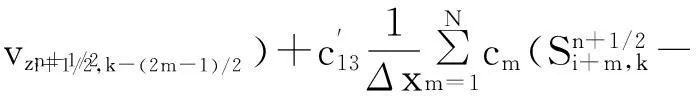
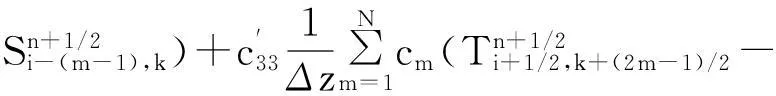
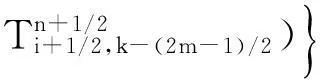
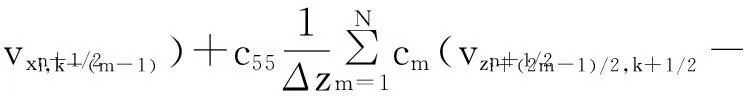
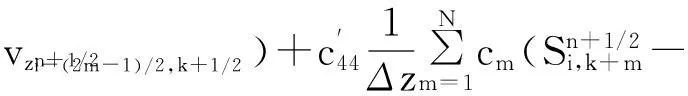
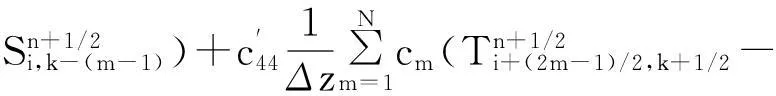
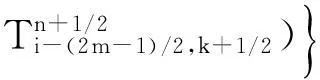
(3)

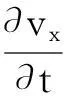
1.3頻散壓制方法

在求解一階應力速度方程時，以差分形式代替微分形式對方程進行網格剖分，原本連續的介質和波場函數就被離散化，因而不可避免地引入了數值頻散也稱為偽波動，這種偽波動對研究地震波的波場特征和傳播規律干擾非常大。因此對數值頻散的有效壓制方法研究，則尤為重要。

為了消除這種頻散，常用的手段是引入FCT(通量校正傳輸)方法[8]進行壓制，雖然常規的FCT可以比較好地壓制頻散，但是η1、η2(η1擴散通量校正參數，η2反擴散通量校正參數)兩個參數不好選擇，而且經過FCT后難免會留有一些未被壓制的偽波動(尤其是η1、η2選擇不當的時候，這種情況更加普遍)。這里對常規的FCT方法加以改進，進而提高頻散壓制效果。主要包括七個步驟：

1)通過離散化后的一階應力速度方程，理論上可以計算出任意時刻的速度和應力值，以對速度分量vx做FCT頻散壓制為例，求出得到n和n+1時刻速度分量vx的值。

2)計算n時刻的彌散通量Qx、Qz：

(4)

其中，η1∈[0,1]可以通過考查地震道的振幅變化情況得到。

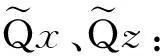
(5)

與η1一樣η2的值也是在0～1之間，但是η2一般要比η1稍大。

4)利用彌散通量Qx、Qz對速度分量vx進行修正，這主要是對速度分量vx的波形行平滑處理，同時也會造成振幅損失。

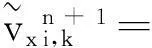
(6)

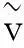
(7)

6)通量反彌散處理，得到校正后的速度vx。

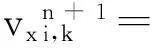
(8)

其中：

(9)

7)濾波處理。得到校正后的速度vx，選擇一個矩形窗口作為vx i,k的實心鄰域。得到實心鄰域內所有的速度值后，計算所得它們的平均值用于代替vx i,k的值。

(10)

2數值模擬結果

本次研究建立了粘彈性各向異性介質模型，然后通過交錯網格算法來實現介質中地震波的數值模擬，并運用改進的FCT方法來壓制數值頻散效應，以便于研究其波場特征和傳播規律。

2.1單層模型

理論研究表明與高速層比較而言，對于低速層所能引起的頻散就更為嚴重。所以，為了檢驗改進后的FCT方法頻散壓制效果，設計了一個單層低速模型。模型大小為2 000m×2 000m，空間采樣步長Δx=Δz=10m，時間采樣率為1ms，使用雷克子波作為震源子波，主頻30HZ，震源坐標為(1 000m，1 000m)。其余參數設定見表1。

表1　單層模型介質參數

圖1為粘彈性介質中對于不同參數(η1，η2)條件下單層低速模型在500 ms時的時間切片,為了便于對比且不失一般性，在此只對比水平方向速度分量的頻散壓制效果。

從圖1中可以看出，當η1=0.0、η2=0.0此時相當于沒做品散壓制處理，時間切片圖1(a)、圖1(b)兩者內部數值頻散比較嚴重，信噪比很低，真實波場模糊不清；當η1=0.014、η2=0.017數值頻散得到一定的壓制，但是由于壓制程度不足，圖1(c)中的頻散仍然很明顯。不過與圖1(c)相比，圖1(d)使用優化后的FCT方法時間切片整體變得更加干凈、清晰；隨著參數的取值逐漸增大，頻散壓制效果得到進一步改善；當η1=0.035、η2=0.041時，圖1(e)、圖1(f)波場更加圓滑，信噪比得到提高，內部的偽波動得到較好地壓制，也可以看出這時候的圖1(f)效果要比圖1(e)明顯更好，對圖1(f)而言，參數η1、η2已經快接近頻散壓制效果的最優參數。當η1=0.051、η2=0.060時，地震波的真實波場得到了很好地恢復，能量也得到了補償，圖1(g)、圖1(h)的內部已經基本看不到頻散、此時可以將η1、η2認為是最優參數。通過圖1對比說明，η1、η2的選擇對頻散壓制效果有直接影響，只有合適的η1、η2才能有效地對數值頻散進行壓制。模擬結果表明：在壓制效果上優化后的FCT方法要比常規的FCT方法更好；在最優參數的選擇上改進后FCT方法也比常規的FCT更具有適用性。

為了進一步對比優化后的FCT方法和常規的FCT方法，對圖1中相應的時間切片抽取其第75道記錄進行比較，圖2(a)由于振動曲線跳動劇烈，從曲線上已經很難將真實波場所引的振動和頻散造成的偽振動區分開來，這正好與時間切片圖1(a)、圖1(b)中嚴重的數值頻散相吻合；圖2(b)、圖2(c)隨著參數η1、η2取值增大，頻散壓制后的曲線變得平滑，大約在橫坐標50～100處，此時可以看到，使用優化后的FCT方法得到的結果，要比常規FCT方法得到的振動曲線質點振動更平緩，說明優化后的FCT方法能更好地消除頻散；圖2(d)中兩條曲線接近重合，可以看出完整的雷克子波波形、此時已經沒有了頻散帶來的干擾振動。我們可以認為在相同的η1、η2取值時，優化后的FCT方法可以取得更好的頻散壓制效果，該方法比常規的FCT方法能更好地保持真實波場特性。

2.2三層模型

設計一個三層模型，進一步分析研究粘彈性介質中地震波的傳播規律、振幅和頻率衰減情況。當品質因子取值很大時，表明介質不再具有粘彈性而轉化成了彈性介質。模型大小為2 000 m×2 000 m，空間采樣步長Δx=Δz=10 m，時間采樣率為1 ms，使用雷克子波作為震源子波，主頻30 Hz。震源坐標為(1 000 m,100 m)，其余參數設定見表2。

表2　三層水平層狀模型介質參數

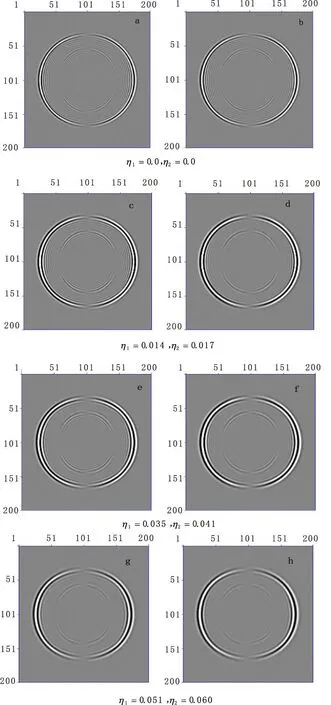
圖1　常規FCT與優化后FCT頻散壓制效果對比Fig．1　Comparison of the suppress dispersion effect of conventional 　　　FCT and optimized FCT(a)常規FCT ，(b)優化后FCT；(c)常規FCT ，(d)優化后FCT；(e)常規FCT ，(f)優化后FCT；(g)常規FCT ，(h)優化后FCT

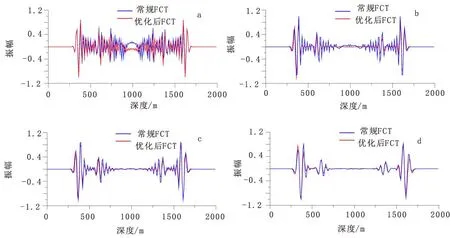
圖2　圖1中相應時間切片抽取其第75道記錄振幅對比Fig．2　The seventy-fifth record amplitude comparison of corresponding time slice in figure 1(a)η1=0.0,η2=0.0;(b) η1=0.014,η2=0.017;(c) η1=0.035,η2=0.041;(d) η1=0.051,η2=0.060

圖3是三層模型共炮點地震記錄，可以看到直達波和來地層反射界面的反射波。對比水平分量地震記錄圖3(a)、圖3(b)，雖然兩者的反射同向軸都可以比較清晰地看到，但是圖3(b)中經過吸收衰減后同向軸能量比圖3(a)的要弱、比較暗淡，大約在1.1 s時刻圖3(a)、圖3(b)它們的同向軸差異最明顯。由于水平方向上炮點左右兩邊接收到的地震波起振方向不一致，因而出現了極性反轉；而此時在垂直方向上炮點左右兩邊接收到的地震波起震方向都是一致的(與深度方向相反)，所以圖3(c)、圖3(d)中沒有出現極性質反轉現象。在垂直方向上的地震記錄圖3(c)、圖3(d)，大約1 s后圖3(c)中同向軸可以較為清晰地觀察到，但是此時圖3(d)中由于粘彈性介質對波場的吸收作用，使得其反射同向軸已經基本上不能識別。

圖4是在前面圖3中三層模型共炮點地震記錄的基礎上，分別抽取了彈性介質和粘彈性介質第75道地震記錄切除掉直達波后做振幅能量對比(圖3中黑線即為抽取的地震道位置)。圖4從另一個角度揭示了粘彈性介質對地震波的吸收衰減作用，可以看出，水平方向圖4(a)的振幅比垂直方向圖4 (b)的稍強。圖4中1.1 s后粘彈性記錄振幅基本衰減零，這與圖3中在1 s左右觀察到的粘彈性介質中反射波能量衰減結果相吻合，同時也看出粘彈性介質不僅對地震波的振幅起到了衰減作用，也使得地震波的波形發生了畸變。

為了便于定量分析衰減所引起的能量變化，圖5是對彈性與粘彈性介質中的模擬結果中第75道記錄進行頻譜分析。從圖5中觀察到，粘彈性記錄的主頻發生了變化，向小于主頻30 Hz的方向移動。同時粘彈性記錄的頻譜低頻部分有所增加而高頻部分相應減少。

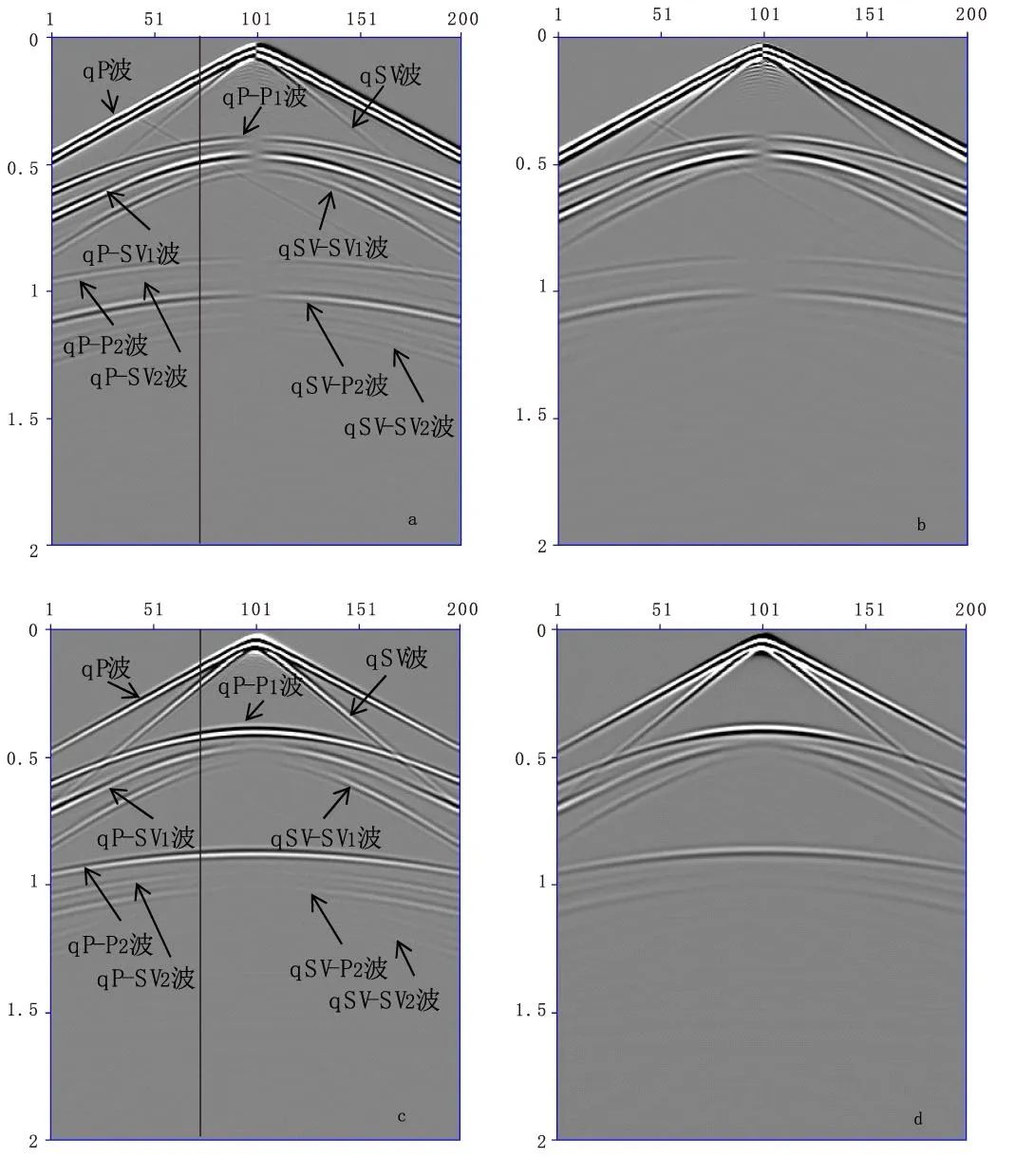
圖3　三層模型共炮點地震記錄Fig．3　The common shot seismic record of three-layer model(a)彈性水平分量；(b)粘彈性水平分量；(c)彈性垂直分量；(d)粘彈性垂直

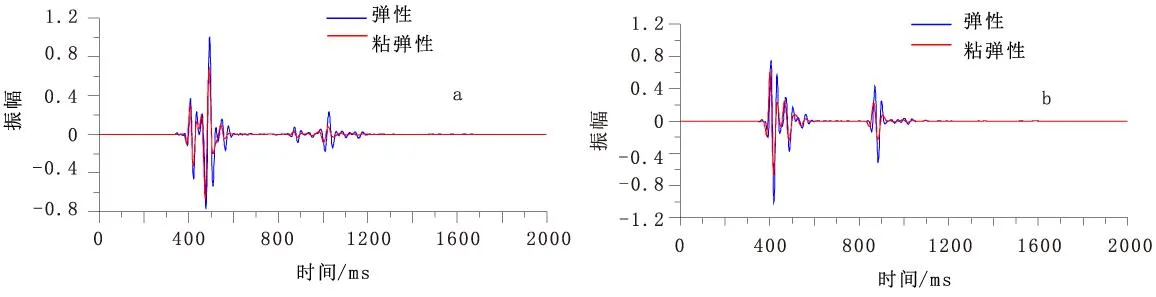
圖4　圖3中第75道彈性記錄與粘彈性記錄振幅對比Fig．4　The elastic and viscoelastic seismogram amplitude contrast of the 　　　seventy-fifth record in figure 3(a)水平分量；(b)垂直分量

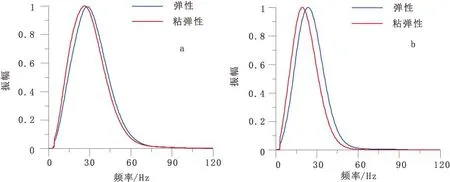
圖5　圖3中第75道彈性記錄與粘彈性記錄頻譜對比Fig．5　The elastic and viscoelastic seismogram spectral contrast of the 　　　seventy-fifth record in figure 3(a)水平分量；(b)垂直分量

3結論

通過對粘彈性介質中地震波的數值模擬結果對比分析發現，在對一階應力速度方程離散時不可必可避地帶入了數值頻散。作者提出優化后的FCT(通量校正傳輸)方法能夠有效地解決數值頻散問題，在頻散壓制參數η1、η2的選擇上更具適用性，對于同樣的η1、η2取值優化后的FCT方法在頻散壓制效果上也要比常規的FCT方法要好。

粘彈性介質對地震波的波場有吸收衰減作用，這種吸收衰減與品質因子有著一定聯系。粘彈性介質除了會使得地震波的振幅能量發生衰減外，也會導致地震波的相位發生變化，并且主頻也會隨之衰減；在水平方向上地震記錄有極性反轉現象。

地震波數值模擬對解決和認識實際波場特征問題有重要的指導意義，同時也因為地下介質真實情況較為復雜，要徹底認識復雜粘彈性介質中地震波的傳播規律還需要進一步研究。

參考文獻：

[1]N．H．瑞克．粘彈性介質中的地震波[M]．許云，譯．北京：地質出版社，1981．

N H RICK. Seismic wave in viscoelastic media[M]. XU Y，translation. Beijing: Geological Publishing House,1981.(In Chinese)

[2]牛濱華，孫春巖． 半無限空間各向同性粘彈性介質與地震波傳播[M]． 北京: 地質出版社，2007．

NIU B H, SUN C Y. Semi-infinite space isotropic viscoelastic medium and seismic wave propagation[M].Beijing: Geological Publishing House, 2007.(In Chinese)

[3]張劍鋒，李幼銘．水平層狀介質中粘彈性波的計算[J]．計算結構力學及其應用，1994，11(3)：314-324．

ZHANG J F, LI Y M. Horizontally layered viscoelastic wave of computing[J]. Computational Structural Mechanics and its Applications, 1994，11(3)：314-324．(In Chinese)

[4]畢玉英，楊寶俊．二維粘彈性介質中完全波場正演模擬[J]．石油地球物理勘探，1995，30(3)：351-362．

BI Y Y, YANG B J. 2-D viscoelastic medium completely wave forward modeling [J]. oil geophysical prospecting, 1995，30(3)：351-362．(In Chinese)

[5]孟凡順，郭海燕．復雜地質體粘滯彈性波正演模擬的有限差分法[J]．青島海洋大學學報，2000，30(2)：315-320．

MENG F S, GUO H Y. Finite difference method for forward modeling of complex geologic body with viscous elastic wave[J]. Journal of Qingdao ocean university, 2000，30(2)：315-320．(In Chinese)

[6]杜啟振，楊慧珠.裂縫性地層粘彈性地震多波波動方程[J].地球物理學報，2001(08)：2801-2806.

DU Q Z, YANG H Z. The fracture formation of Multiwave viscoelastic seismic wave equation[J]. Chinese Journal of Geophysics，2001(08)：2801-2806. (In Chinese)

[7]唐啟軍,韓立國,王恩利.基于隨機各向同性背景的粘彈性單斜介質二維三分量正演模擬[J].西北地震學報,2009,31(1):35-39.

TANG Q J, HAN L G, WANG E L. Forward modeling of three component of viscoelastic medium based on random isotropic background[J].Journal of Northwest China,2009,31(1):35-39. (In Chinese)

[8]賀同江，劉紅艷，李小凡.粘彈性介質地震波傳播的褶積微分算子法數值模擬研究[J].西北地震學報,2010,32(4):318-324.

HE T J, LIU H Y, LI X F. Numerical simulation of the convolution differential operator method for seismic wave propagation in viscoelastic media[J].Journal of Northwest seismology,2010,32(4):318-324. (In Chinese)

[9]BOOK D L，BORIS J P，HAIN K．Flux-corrected trans-port,II: generalization of the method[J]．Computational physics，1975，18: 248-283．

[10]楊頂輝，藤吉文.各向異性介質中三分量地震記錄的FCT 有限差分模擬[J]．石油地球物理勘探,1997,32( 2):181-190．

YANG D H,TENG J W. FCT finite difference simulation of three component seismic records in anisotropic media[J].oil geophysical prospecting,1997,32( 2):181-190．(In Chinese)

[11]董良國,李培明.地震波傳播數值模擬中的頻散問題[J].天然氣工業, 2004, 24(6): 53-56.

DONG L G, LI P M. Frequency dispersion in numerical simulation of seismic wave propagation[J]. Gas Industry, 2004, 24 (6): 53 -56. (In Chinese)

[12]陳可洋. 地震波數值模擬中優化的通量校正傳輸方法[J].內陸地震,2012, 26(2): 169-179.

CHEN K Y, Optimal flux corrected transport method in numerical simulation of seismic wave[J].Inland earthquake,2012, 26(2): 169-179. (In Chinese)

[13]李錄明,羅省賢.多波多分量地震勘探原理及數據處理方法[M].成都：成都科技大學出版社,1997.

LI L M, LUO S X. Multi component seismic exploration principle and data processing method[M].Chengdu:Chengdu University of Science and Technology Publishing House.1997. (In Chinese)

[14]韓翀.地震波數值模擬及波場特征分析[D].成都：成都理工大學,2007.

HAN C. Seismic wave numerical simulation and wave field characteristic analysis[D]. Chengdu:Chengdu University of Technology, 2007. (In Chinese)

[15]KINDELAN M，KAMEL A，SGUAZZERO P．On the construction and ef ciency of staggered numerical differentiators for the wave equation[J]．Geophysics，1990，55(1) : 107 -110．

[16]ROBERTSSON J O A，BLANCH J O，SYMES W W．Viscoelastic finite-difference modeling[J]． Geophysics，1994，59(9) : 1444 -1456．

[17]VIRIEUX J．P-SV wave propagation in heterogeneous Velocity-stress finite-difference method[J] ．Geophysics，1986，51: 889-901．

Study on seismic wave simulation of viscous anisotropic media using the improved FCT method

LI Qin-wua,b,c, ZHOU Huai-laia,b,c

(Chengdu University of Technolog a.College of Geophysics，b.State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation,c.Key Lab of Earth Exploration & Information Techniques of Ministry of Education，Chengdu610059，China)

Abstract:Compared to elastic media, the viscoelastic anisotropic media is more practical subsurface characterization in seismic exploration. In this paper mainly aimed at the Kelvin model, Derived the first order stress velocity equation from constitutive equations, geometric equations and differential equations. Then, the numerical simulation of the staggered grid finite difference is used to discrete it and research wave field characteristics and propagation of seismic waves. At the same time, the analysis of the influence of quality factor Q on the attenuation and absorption of seismic wave in amplitude and frequency. Use staggered grid algorithm would inevitably result in numerical dispersion or aliasing phenomenon in numerical simulation, and thus the correctness of the results of the numerical simulation is disturbed. In order to improve the results of numerical simulation, optimized the conventional FCT (flux corrected transport) method to suppress dispersion. Simulation examples demonstrate that the optimized FCT method is more effective than the conventional FCT method in eliminating frequency dispersion.

Key words:Kelvin model; first-order rate equation stress; numerical simulation; quality factor Q; the optimized FCT

中圖分類號：P 631.4

文獻標志碼：A

DOI：10.3969/j.issn.1001-1749.2016.01.11

文章編號：1001-1749(2016)01-0074-09

作者簡介：李勤武(1991-)，男，碩士，從事地震數據處理及波場正演模擬研究，E-mail：liqinwu04@163.com。

基金項目:國家自然科學基金(41204091)

收稿日期：2015-08-07改回日期：2015-09-08