動態規劃最優控制在非線性系統中的應用

陳瑤張剛

摘要：應用一種新的自適應動態最優化方法（ADP），在線實現對非線性連續系統的最優控制。首先應用漢密爾頓函數（HamiltonJacobiBellman， HJB）求解系統的最優控制，并應用神經網絡BP算法對漢密爾頓函數中的性能指標進行估計，進而得到非線性連續系統的最優控制。同時引進一種新的自適應算法，基于參數誤差，在線實現對系統進行動態最優求解，而且通過李亞普諾夫方法對參數收斂情況也進行詳細的分析。最后，用仿真結果來驗證所提出的方法的可行性。

關鍵詞：最優控制；動態規劃；神經網絡；自適應算法；漢密爾頓函數

中圖分類號：TP273.1文獻標識碼：A

1 引言

最優控制是最近幾年國內外新起的一個研究領域，最優控制就是尋找最節能最經濟的控制策略。50年代，美國數學家Bellman為了解決非線性最優控制問題提出了動態規劃方法（Dynamic Programming）[1]。動態最優化方法就是將最優化問題分多級討論，尋求每一級的最優策略，從而達到全局最優。然而在實際問題中對于大量存在的非線性系統，需要求解漢密爾頓函數（HJB），由于維數問題，求解函彌爾頓函數是個很難解決的問題。

強化學習（Reinforcement learning）[2]是基于生物學習的新型理論。通過比強化學習和動態規劃，Werbos[3]提出了新的自適應動態規劃方法，從而解決了離散系統的動態最優求解的“維數災難”問題[1， 4]。然而傳統的增強學習方法一般用來解決離散系統，實際問題往往是連續的。

文獻[5]將增強學習方法和動態規劃方法結合，提出了自適應動態規劃方法（Adaptive dynamic Programming）。Werbos[6]基于增強學習方法，提出評價和執行網對離散系統進行動態最優求解。Lewis[7]提出了一種新的基于神經網絡的自適應動態最優方法對離散非線性系統進行離線求解。

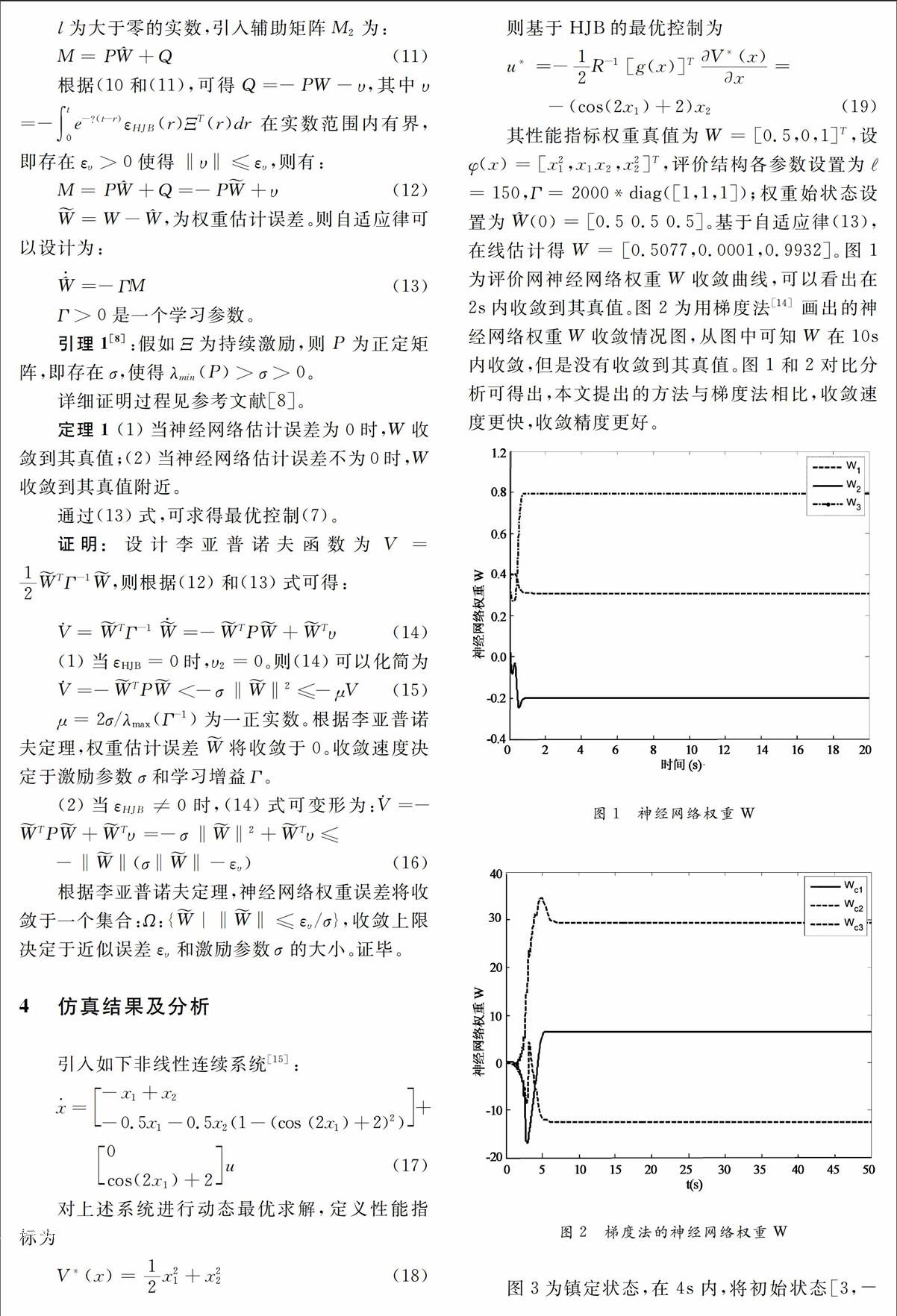
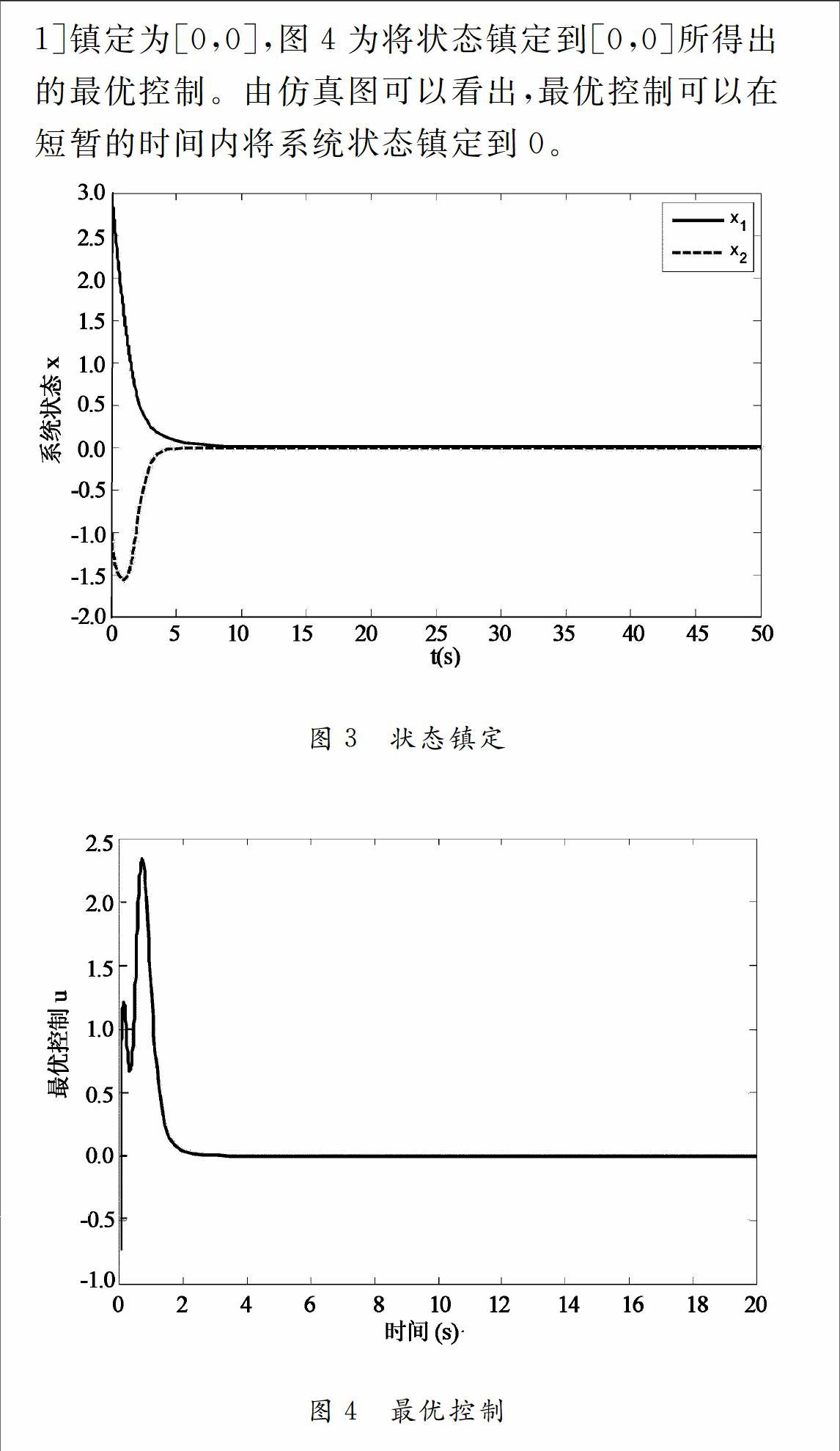
本文基于一種新的自適應動態規劃算法在線解決了非線性系統的最優控制問題。首先應用HJB對非線性系統進行最優求解，進而基于神經網絡方法對最優控制中的性能指標進行估計，即應用評價結構解決了動態最優控制問題，同時省去了傳統最優控制求解問題中的執行機構，很大程度上縮短了計算機計算的時間。文中引用了一種新的自適應算法[8， 9]在線求得基于神經網絡的評價網的權重參數。最后本文對估計權重做了基于李亞普諾夫的收斂性分析，很大程度上提高了論文所提出理論的使用價值。

5結論

引進一種新的自適應算法對非線性連續系統進行自適應動態最優求解。不同Werbos[6]提出的評價執行結構，本文基于辨識評價結構，在線對連非線性系統進行最優求解。用神經網絡逼近性能指標，而且基于自適應估計誤差，在線估計神經網絡權重。比現有文獻所用梯度法和迭代法收斂速度更快，而且收斂效果更加良好。仿真結果更加有力的證明所提出方法的有效性。

參考文獻

[1]B. R. E， Dynamic programming， Princeton： Princeton University Press， 1957.

[2]SUTTON R S，BARTO A G.Reinforcement learning： an introduction. Cambridge Univ Press， 1998.

[3]WERBOS P J.Approximate dynamic programming for real-time control and neural modeling， Handbook of intelligent control： Neural[J].fuzzy， and adaptive approaches，1992， 15： 493-525.

[4]DREYFUS S E，LAW A M.Art and theory of dynamic programming[M].New York： Academic Press， 1977，56.

[5]MURRAY J J，COX C J，LENDARIS G G， et al. Adaptive dynamic programming， Systems， Man， and Cybernetics， Part C： Applications and Reviews[J]. IEEE Transactions on， 2002， 32（2）： 140-153.

[6]WERBOS P J.A menu of designs for reinforcement learning over time[J].Neural networks for control， 1990：67-95.

[7]ABUKHALAF M，LEWIS F L.Nearly optimal control laws for nonlinear systems with saturating actuators using a neural network HJB approach[J].Automatica， 2005， 41（5）： 779-791.

[8]NA J，HERRMANN G，REN X.， et al. Robust adaptive finitetime parameter estimation and control of nonlinear systems[J].IEEE International Symposium on in Intelligent Control （ISIC）， 2011： 1014-1019.

[9]Na. Jing， Ren. Xuemei， Zhang. Dongdong， Adaptive control for nonlinear purefeedback systems with highorder sliding mode observer[J]. IEEE transactions on neural networks and learning systems， 2013， 24（3）： 370-382.

[10]VAMVOUDAKIS K G，LEWIS F L.Online actorcritic algorithm to solve the continuoustime infinite horizon optimal control problem[J]. Automatica， 2010，46（5）：878-888.

[11]VRABIE D，LEWIS F.Neural network approach to continuoustime direct adaptive optimal control for partially unknown nonlinear systems[J]. Neural Networks， 2009，22（3）： 237-246.

[12]DIERKS T，THUMATI B T，JAGANNATHAN S.Optimal control of unknown affine nonlinear discretetime systems using offlinetrained neural networks with proof of convergence[J].Neural Networks， 2009，22（5）：851-860.

[13]LIU D，WEI Q.Finite approximation error based optimal control approach for discretetime nonlinear systems[J].IEEE Transactions on Cybernetics，2013，43（2）：779-789.

[14]BHASIN S，KAMALAPURKAR R，JOHNSON M， et al.A novel actorcriticidentifier architecture for approximate optimal control of uncertain nonlinear systems[J].Automatica，2013，49（1）：82-92， .

[15]NEVISTI V，PRIMBS J A.Constrained nonlinear optimal control： a converse HJB approach，1996.