基于畦灌灌水效果的土壤入滲參數預測精度控制研究

雷國慶，樊貴盛

(太原理工大學，太原 030024)

畦灌作為我國主要的地面灌溉方式之一，其灌水效果受畦長、單寬流量、灌水時間、土壤入滲參數、田面坡度及糙率等因素影響，其中土壤入滲參數對其影響顯著[1]。在畦灌灌水過程中，土壤水分入滲特性直接影響著田面水流的推進及消退過程，直接對灌水后土壤水分的分布造成影響，灌水效果可能出現顯著差異。因此，合理選取土壤入滲參數對畦灌灌水效果改善具有重要意義。然而，由于土壤入滲能力空間變異性的存在，區域尺度上的入滲參數獲取較為困難，基于此，學者們試圖建立關于入滲參數的土壤傳遞函數[2]，利用較易獲取的土壤理化參數對土壤入滲參數進行預測，其中曹崇文[3]以不同深度上的土壤密度、含水率、質地、有機質含量等為已知參數，試圖建立線性、非線性和人工神經網絡等模型對土壤入滲參數進行預測。然而由于不同預測模型得到的預測精度有較大差異，預測精度的差異是否會對畦灌灌水效果產生影響，產生的影響是否可被接受尚缺乏有效驗證。

在地面灌溉領域，土壤入滲參數的精度控制需建立在灌水效果指標對入滲參數變化敏感程度的基礎上。學者們在入滲參數空間變異對灌水質量影響方面作了較多研究，其中朱艷等[4]選用兩參數Kostiakov模型，認為灌水均勻度和灌水效率對入滲參數k、α的響應關系均為單峰二次曲線，并且入滲參數k穩定區間較α大；王維漢等[5]基于穩健設計理論，通過正交試驗進行敏感性分析，認為對灌水質量影響較大的因素依次為單寬流量q、入滲指數α、入滲系數k。但如何利用灌水效果對入滲參數變異的敏感性，建立土壤入滲參數精度控制模型尚未得到有效解決。在前人研究的基礎上，本文以汾東灌區北長壽的灌水試驗為背景，對試驗點的灌水技術參數組合進行多目標模糊優化[6]，在此基礎上，以優化灌水技術參數為固定參數，將土壤入滲參數k、α和f0進行不同程度的偏離，利用地面灌溉模擬軟件WinSRFR[7]對不同入滲特性下的畦灌灌水效果進行模擬，通過灌水效果敏感性分析結合灰色關聯理論[8]，以期建立土壤入滲參數預測精度控制模型。

1 畦灌灌水模型及評價指標

1.1 土壤水分入滲模型

為有效地對土壤入滲性能進行表征，選用應用范圍最廣的Kostiakov三參數入滲經驗模型[9]。該模型形式簡單、擬合精度高，其表達式如下：

Z=ktα+f0t

(1)

式中：Z為累積入滲水深，mm；k為土壤入滲系數，mm/s；t為入滲時間，s；α為入滲指數；f0為常數項，mm/s。

由式(1)可知，土壤入滲參數k、α、f0反映土壤的入滲特性，不同的入滲參數組合土壤入滲能力不同 。其中當t→0時，k=Z，表示土壤在初始時刻的入滲能力；在水分入滲過程中，入滲指數α表征土壤水分入滲能力的衰減速度，反映土壤水分入滲特性曲線的飽滿程度；而t→∞時，f0=Z′,即入滲參數f0指土壤在達到飽和后的穩定入滲速率。

1.2 田面水流運動模型

對于水平畦田，圣維南動量方程中的加速項和慣性項均可考慮不計，田面水流運動選用零慣量模型[10]進行模擬：

(2)

式中：A為田面水流的斷面面積，m2；Q為田面水流流量,m3/s；x為沿畦長方向距畦首的距離，m；H為累積入滲水深，m；S0為田面坡度；Sf為阻力坡度。

1.3 畦灌灌水效果評價指標

對畦灌灌水效果評價，目前應用最為廣泛的灌水效果評價指標包括灌水效率Ea、儲水效率Es和灌水均勻度Du[11]。其中Ea為灌水效率，從節水的角度考慮，用來評價灌溉水的利用效率；Es為儲水效率，與作物的產量相關，反映某次灌水后計劃灌水量的滿足程度；Du為灌水均勻度，指某次灌水后土壤水分入滲深度沿畦田縱向分布的均勻程度，考慮整個畦田的灌水質量。三者的計算公式如下：

(3)

式中：Dz為某次灌水后儲存于土壤計劃濕潤層的平均深度，mm；Dapp為灌入田間的平均灌水深度，mm；Ddp為灌水過程中深層滲漏的平均深度，mm；Dro為畦田平均棄水深度，mm；Dreq為田間計劃灌水深度，mm；Dlq為沿畦長方向上土壤受水最少的1/4段內的平均入滲水深，mm；Dinf為畦田田塊上的平均入滲水深，mm。

2 灌水技術參數組合優化

2.1 試驗點基本灌水資料

試驗點位于汾東灌區北長壽，以試驗麥田為代表，根據試驗點的地形條件、田間工程規格、土壤狀況以及實際灌水制度，確定畦田長度L和單寬流量q，具體范圍見表1。試驗點的土壤入滲參數(α，k，f0)、田面坡度i、田間糙率值n選取試驗點各測點的平均值，取值見表1。計劃灌水深度由土壤的凋萎系數和田間持水量決定，本文選用90 mm。

表1 汾東灌區北長壽試驗點基本灌水資料

2.2 灌水技術參數的多目標模糊優化

本文以灌水效率Ea、儲水效率Es和灌水均勻度Du為目標函數，畦長L、單寬流量q和灌水時間t為決策變量，建立多目標優化模型：

(4)

式中：G1為畦灌灌水效率目標函數；L為畦田長度，m；q為入畦單寬流量,L/(s·m)；t為灌水時間，min；G2為儲水效率目標函數；G3為灌水均勻度目標函數；Lmax、Lmin分別為畦田最大、最小長度；qmax、qmin分別為允許入畦最大、最小單寬流量，見表1。

利用WinSRFR對不同灌水技術參數組合下的灌水效果進行模擬，將模擬結果進行回歸分析，確定目標函數形式，分別先在單目標條件下對目標函數進行優化，然后根據目標函數的模糊性，引入線性隸屬度函數，根據實際灌水經驗確定各單目標優化結果的伸縮指標，按照最大隸屬度原則，將多目標優化問題轉化為一個單目標非線性優化問題，從而得出最優灌水技術參數組合，本文選取畦長L為200 m的優化灌水技術參數組合：L=200 m，q=3.2 L/(s·m)，t=93 min，此條件下的灌水效果為：Ea=96.4%，Es=95.56%，Du=89.94%。

3 土壤入滲參數預測精度控制

為實現基于畦灌灌水效果的土壤入滲參數預測精度模型，本文在優化灌水條件下，將土壤入滲參數k、α和f0進行不同程度的偏離，分析灌水效果指標的敏感響應程度，在此基礎上，對各灌水效果指標與入滲參數間的灰色關聯度進行分析，并利用灰色關聯系數確定入滲參數k、α、f0的預測精度對灌水效果指標的影響權重，通過對畦灌灌水效果指標的誤差進行約束，實現土壤入滲參數的預測精度控制。

3.1 灌水效果指標對入滲參數的敏感性分析

為分析灌水效果指標對入滲參數變化的敏感響應程度，根據實際入滲參數的變異情況，以及土壤傳遞函數中入滲參數常見的預測精度大小，考慮以試驗點實測入滲參數k、α、f0為基準，進行上下一定程度的偏離(以5%為步長，上下最大偏離為基準的30%)，分析在不同入滲參數條件下灌水效果指標的變化程度(以較基準條件下灌水效果指標的相對誤差ε表示) ，見圖1。

由圖1可知，各灌水效果指標對入滲參數k、α、f0偏離的敏感程度不同，灌水效率Ea和儲水效率Es的敏感程度相當，對入滲參數變化反應相對較小，即使入滲參數的偏離度達30%時，Ea、Es的相對誤差也控制在5%以下(此處暫不考慮各入滲參數偏離的綜合影響)。而灌水均勻度Du對入滲參數變化較為敏感，當入滲參數k、f0的偏離程度達15%左右時，其相對誤差可達5%左右；當入滲參數k、f0的偏離程度達30%左右時，Du的相對誤差向10%逼近。

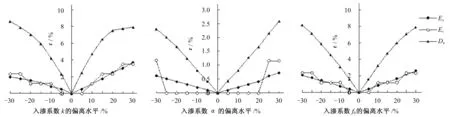
圖1 土壤入滲參數k、α、f0偏離對灌水效果的影響

各入滲參數的變化對灌水效果的影響大小也不同，入滲參數k、f0變化對灌水效果的影響明顯強于參數α的影響。入滲參數k、f0偏離15%左右，Ea、Es相對誤差接近2%，Du相對誤差接近5%，而入滲參數α偏離30%，Ea相對誤差未達1%，Es相對誤差未達1.5%，Du相對誤差也未達3%。

3.2 灌水效果指標與土壤入滲參數的灰色關聯分析

為分析各入滲參數與不同灌水效果指標間的關聯程度，本文利用均勻試驗設計的方法，選擇U*13(133)均勻試驗表[12]，對土壤入滲參數k、α、f0按上述不同偏離水平下的灌水效果指標進行模擬，結合WinSRFR模擬軟件，模擬結果見表2。

現以表2中灌水效果評價指標灌水效率Ea、儲水效率Es和灌水均勻度Du為參考序列x0(n)，n=1,2,…,13，而k、α、f0作為比較序列xi(n)，i=1,2,3，其中x0(n)、xi(n)表示x0、xi的第n個實數。

首先對各因素進行進行無量綱處理：

(5)

求差異序列：

Δ0i(n)=|y0(n)-yi(n)|

(6)

確定Δmin=minΔ0i(n)，Δmax=maxΔ0i(n)，并計算關聯系數如下：

(7)

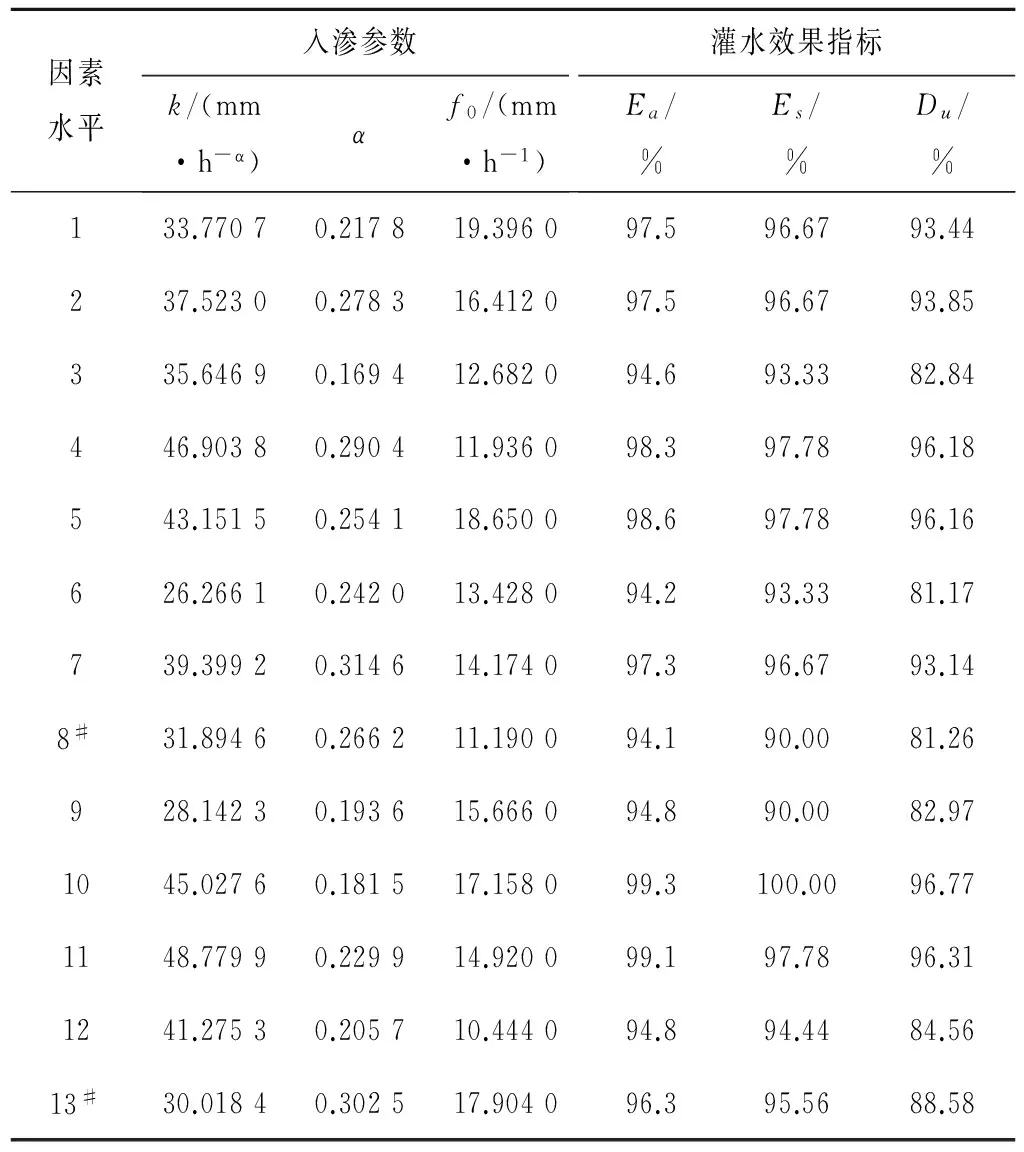
表2 均勻試驗方案及模擬結果

式(7)中ρ∈(0，1]，為分辨系數，由于參考序列數據平穩，此處選用較大的分辨系數1。

則各入滲參數的關聯度r0i為：

(8)

根據上述方法，可得各灌水效果指標與入滲參數間的灰色關聯度，見表3。

灰色關聯分析結果顯示，對于灌水效果指標Ea、Es、Du而言，各入滲參數與其灰色關聯程度由大到小為：k>f0>α。由此可見入滲系數k與灌水效果指標關聯程度較為密切，入滲參數f0次之，入滲指數α與灌水效果指標關聯性較小。

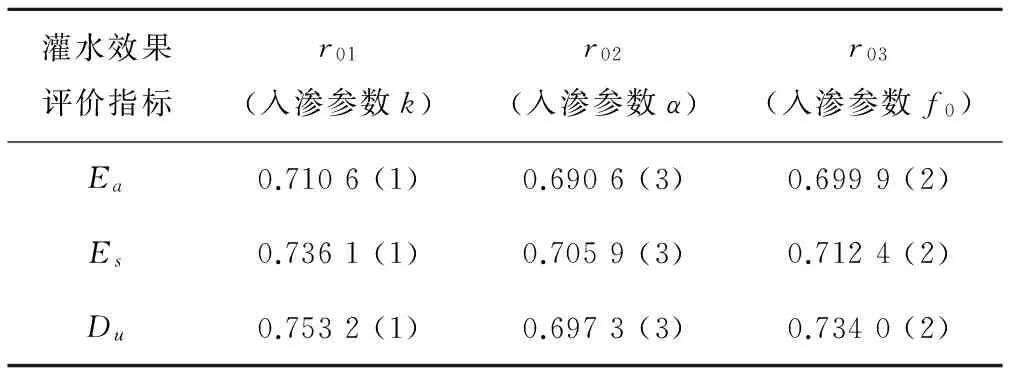
表3 均勻試驗方案及模擬結果

3.3 土壤入滲參數的預測精度控制

在其他灌水技術參數一定的情況下，畦灌灌水效果的誤差受土壤入滲參數k、α、f0精度的綜合影響，因而要降低灌水效果誤差，需全面考慮土壤入滲參數k、α、f0的精度問題。上述只分析了單因素入滲參數偏離情況下的灌水效果指標相對誤差，而灌水效果指標的實際總相對誤差不能由單個入滲參數偏差引起的灌水效果誤差簡單直接相加，基于此，本文擬考慮灌水效果指標的總誤差為各入滲參數引起的灌水效果誤差的加權和。根據灌水效果指標與入滲參數間的灰色關聯度，引入各入滲參數偏差對灌水效果指標誤差的權重系數ξ：

(9)

式中：ξi表示各入滲參數k、α、f0的偏差影響權重，i=1,2,3；r0i為各入滲參數與灌水效果指標的灰色關聯度。

各入滲參數偏差的權重系數見表4。

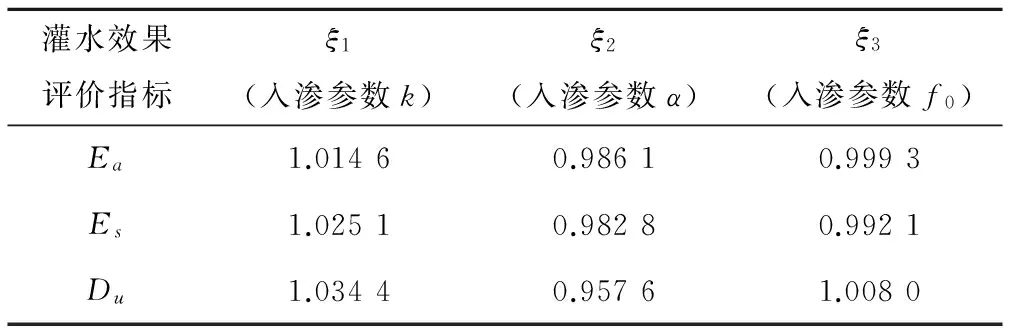
表4 各入滲參數偏差對灌水效果指標誤差的影響權重

由表4可以看出，入滲參數k的權重系數略大，f0的次之，α的權重略小，結合灌水質量要求和實際灌水經驗，對于灌水效率Ea和儲水效率Es，其指標的大小對灌水質量的影響較大，本文考慮兩指標的相對誤差應控制在5%以內，而對于灌水均勻度Du而言，其對灌水質量影響相對于上述兩者相對較小，本文考慮將其相對誤差控制在10%以內。綜上所述，建立土壤入滲參數的預測控制模型：

(10)

由式(10)可知，利用灌水效果指標對入滲參數的敏感性分析結果，結合入滲參數偏差引起的灌水效果指標總相對誤差約束，即可實現入滲參數的預測精度控制。

4 結 論

(1)在優化灌水條件下，各灌水效果指標對入滲參數變化的敏感程度并不一致，土壤入滲參數的預測精度或變異情況主要對灌水均勻度Du產生影響。入滲參數k、f0變異對灌水效果指標的影響相對較大，入滲指數α的影響較小。結合文中建立的入滲參數精度控制模型，在對其進行參數預測時，建議入滲參數k、f0的預測相對誤差應在20%以內，α的預測相對誤差可放寬至30%。

(2)通過對入滲參數變化引起的畦灌灌水效果允許相對誤差進行約束，結合灌水效果指標的敏感度分析，建立了土壤入滲參數預測精度控制模型，為關于入滲參數的土壤傳遞函數模型建立提供了依據。在文中的灌水條件下，權重系數的差異并不明顯，但當灌水條件(單寬流量、灌水時間等)發生變化時，權重系數可能會有較明顯差異。

(3)本文僅通過將各入滲參數對灌水效果指標誤差進行了直接加權相加，并未考慮入滲參數對灌水效果的交叉影響，如何在考慮各入滲參數交互作用的基礎上，建立土壤入滲參數的精度控制模型仍有待進一步的研究。

[1] Oyonarte N A, Mateos L. Accounting for soil variability in the evaluation of furrow irrigation[J]. Transactions of the American Society of Agricultural Engineers, 2003,46(1):85-94.

[2] 黃元仿,李韻珠. 土壤水力性質的估算——土壤轉換函數[J]. 土壤學報,2002,39(4):517-523.

[3] 曹崇文.利用土壤傳輸函數確定入滲參數的方法研究[D].太原: 太原理工大學，2007．

[4] 朱 艷,繳錫云,王維漢,等. 畦灌土壤入滲參數的空間變異性及其對灌水質量的影響[J]. 灌溉排水報,2009,28(3):46-49.

[5] 王維漢,繳錫云,彭世彰,等. 基于穩健設計理論的畦灌質量敏感性分析[J]. 農業工程學報,2010,26(11):37-42.

[6] 劉普寅，吳孟達.模糊理論及其應用[M].長沙：國防科技大學出版社，1998：134-148.

[7] Bautista E, Clemmens A J, Strelkoff T S, et al. Analysis of surface irrigation systems with WinSRFR-Example application[J]. Agricultural Water Management,2009,96(7):1 162-1 169.

[8] 劉思峰,黨耀國,方志耕.灰色系統理論及其應用[M].北京:科學出版社, 2004.

[9] Kostiakov A N．On the dynamics of the coefficient of water percolation in soils and on the necessity of studying it froma dynamic point of view for purposes of amelioration [J]．Soil Sci,1932,97(1)：17-21.

[10] 李遠華，羅金耀.節水灌溉理論與技術[M].武漢：武漢大學出版社,2003：166-173.

[11] 林性粹,王 智,李援農.農田灌水質量指標的分析與評價[J].水利學報, 1996, 30(11)：74-77.

[12] 方開泰，馬長興.正交與均勻試驗設計[M].北京：科學出版社，2001.