一種基于非均勻目標的空間相機平場定標方法

岳巾英,李素文,何玲平

(1.長春工程學院 理學院,吉林 長春　130021;

2.中國科學院長春光學精密機械與物理研究所,吉林 長春　130033)

?

一種基于非均勻目標的空間相機平場定標方法

岳巾英1,李素文1,何玲平2

(1.長春工程學院 理學院,吉林 長春130021;

2.中國科學院長春光學精密機械與物理研究所,吉林 長春130033)

摘要：平場定標是空間相機研制過程中必不可少的定標項目。目前,普遍使用均勻照明目標進行空間相機的平場定標,而該方法由于依賴于目標的均勻性,其應用存在一些缺陷。提出了一種基于非均勻目標的平場定標方法,擺脫了對目標均勻性的依賴,具有實際應用價值。首先,基于多幅非均勻目標圖像像元灰度的相關性,建立了相機像面響應度分布計算模型;采用最小二乘迭代法對該模型進行了求解,并編寫程序進行仿真驗證,驗證結果表明,在圖像信噪比高于25 dB的情況下該方法定標精度優于0.5%;最后,根據該方法的特點,給出了實際定標試驗的操作流程。

關鍵詞：平場定標; 非均勻照明; 空間相機; 模型仿真

引言

空間相機是利用光學技術獲取目標信息的航天有效載荷,是一種獲取地球地理、宇宙天體信息的有力工具,在對地遙感測繪、資源普查、減災防災、國防軍事、空間天文學及空間天氣預報等領域,有著重要的應用價值。為了提高獲取數據的準確性,空間相機一般要進行一些地面和在軌的平場定標試驗。由于CCD等傳感器像元間響應差異性、光學系統的漸暈現象及光學鏈路中元件可能被污染等情況的存在,空間相機像面上不同位置可能存在響應度非均勻性[1-2]。這將導致同一輻射強度目標在像面不同位置成像的圖像灰度輸出不相等,使得相機獲得的數據存在誤差。這種像面響應非均勻性不僅直接影響目標輻射強度的測量精度,而且會在圖像上帶來或亮或暗的陰影,導致圖像分辨性能降質,因此平場定標是空間相機研制過程中的一項重要工作。

平場定標的目的是解決相機像面響應的非均勻性,一般通過對一個人造均勻照明的目標拍攝一幅圖像,即可測量像面上不同像元間響應非均勻性[3]。常用人造均勻照明目標主要有標準漫反射板和積分球光源等,其中標準漫反射板是一種表面涂有漫反射材料的平板,光源輻射光線經其漫反射后強度近似朗伯分布,在一定條件下具有較好的照度均勻性;積分球光源是一種內部漫反射照明、表面有開口的光源,與漫反射板相比其開口處輻射強度更加接近朗伯分布,開口處的照度均勻性更好,可達到較漫反射板更高的定標精度[4-7]。盡管目前制作工藝已有較大的進步,但漫反射板的定標精度一般只能達到5%,而積分球的定標精度也不高于1% 。目前,常用平場定標存在以下困難: 1) 隨著空間相機口徑的增大,對積分球體積的要求會急劇增加,使得試驗成本難以負擔; 2) 在軌的平場定標只能使用定標精度有限的漫反射板方案; 3) 對于真空紫外波段來說,目前尚無該波段的人造均勻照明目標,無法進行平場定標。因此,采用均勻照明物成像的平場定標方法存在一些應用缺陷,需要探討一種新的平場定標方法,克服定標過程中對均勻照明的依賴[8-9]。基于此,本文擬提出一種不需要以均勻照明物為成像目標的平場定標方法。

1非均勻照明平場定標原理推導

對一個理想的、不存在像面響應非均勻性的光學成像系統來說,目標的圖像灰度與目標強度成正比關系,而與目標在像面成像位置無關。實際上,由于成像系統的各像元之間的響應非均勻性、光學系統漸暈、元件污染等原因,像面上不同位置像元的響應系數是不同的,使得目標圖像灰度不再與其強度成正比例關系,式(1)為一個與像面位置相關的函數

(1)

式中:oi為目標實際強度;di為光學成像系統灰度輸出;x為像元位置;r(x)為在像元x處的響應系數;i表示多幅圖像中一幅。通過平移目標或者相機視場偏轉等方式,相機可以拍攝多幅同一目標在像面上偏移不同距離的圖像。如果用o代表目標第一幅圖像拍攝時的強度分布,oi代表拍攝第i幅圖像時目標的強度分布,此時目標像在像面上偏移了像元距離ai。假設在圖像拍攝期間目標的強度是穩定的,兩者關系則為oi(x)=o(x-ai)。此時,兩幅圖像中的像元灰度存在一種相關性,此相關性可以由圖1直觀地表示(圖中P(i)為像元i的灰度),也可以用對應像元的響應度比值來表達

(2)

對式(2)兩邊取對數,設R(x)=ln(r(x)),Di=ln(di),可得

(3)

由于相機系統的像面響應度分布R(x) 是固定的,不隨拍攝次數變化,而Di、Dj是已知采集圖像的灰度分布,因此式(3)是一個關于未知數R(x)的線性方程。如果成像目標能夠覆蓋像面大部分區域,并在像面上以已知的像元偏移間隔采集足夠多圖像,可以實現對像面響應度分布R(x)的過采樣,得到多個與式(3)相同的方程式,從而組成一個可求解的方程組,該方程組中方程數超過未知數個數,是一個關于R(x)的超定線性方程組。

圖1　目標位置偏移圖像灰度相關性示意圖

絕大多數情況下,超定線性方程組沒有古典意義的精確解。最小二乘法是求解超定線性方程組最常用的算法,它能提供一個最接近真實解的近似解,使得殘差的2-范數最小。對于式(3)來說,該超定線性方程組的最小二乘解滿足

(4)

對式(4)關于R(x)微分,得到

(5)

設式(5)的初始解為R0(x)=0,則其迭代解為

(6)

其中

n(x)為求和符號內多項式的數量。

式(6)為式(4)的最小二乘法迭代求解模型,根據該模型編寫程序可以實現相機像面響應系數分布的求解。計算過程中每一次迭代計算都涉及大量矩陣運算,且需要經過多次迭代才能接近精確解,因此計算量頗為巨大,需要使用適合矩陣運算的語言進行編寫。

2模型仿真驗證

為了驗證第1節推導得到的相機像面響應非均勻性的經典最小二乘法求解模型的正確性,本文采用IDL(interface definition language)語言編寫程序實現該模型的求解算法,并建立仿真模型進行驗證。IDL語言是一種常用于航天遙感圖像處理的編程語言,具有面向矩陣、語法簡單的特點,能夠快速分析超大規模的數據,且內置多種高級圖像處理、數學計算算法,比較適合本文工作的進行。

整個仿真過程包括: 1) 模擬生成相機的像面響應度系數分布; 2) 模擬生成一個強度符合高斯分布的成像目標; 3) 模擬該目標在相機像面上的成像,并在圖像中添加隨機噪聲; 4) 模擬該目標在相機像面上位置偏移成一組圖像; 5) 編程實現經典最小二乘法求解模型,并使用該模型對所有位置偏移目標圖像進行處理,求解出最佳迭代解; 6) 計算最佳迭代解與實際生成的像面響應度分布模型的符合度,評價此求解模型的求解精度。

圖2為模擬生成的高斯強度分布目標在像面中心所成的像,圖像的信噪比為200 dB。圖3為模擬生成的相機像面響應度分布,圖4為對所有圖像進行經典最小二乘法求解模型計算獲得的相機像面響應度,逐像元計算圖3和圖4中響應度平均誤差為0.17%。本文分別模擬了圖像信噪比分別為200 dB、100 dB、50 dB、25 dB情況下,評估求解模型的所獲得的平場定標結果精度,結果如表1所示。將實際像面像面響應度系數分布與求解的像面響應度系數分布相減得到像面響應度系數求解誤差,提取其中心一行并顯示如圖5至圖8。從上述圖表中可以看出,不同圖像信噪比值下,對應最大的平場定標相面響應度最大偏差為0.47%,因此基于非均勻照明目標的平場定標方法定標精度較高,具有較大的實用價值。

圖2　高斯目標仿真圖像

圖3實際像面響應度分布

圖4　定標得到像面響應度分布

序號圖像信噪比/dB最大偏差/%平均偏差/%12000.610.1721000.890.203501.410.284252.440.47

圖5　S/N=200 dB像面響應度系數誤差

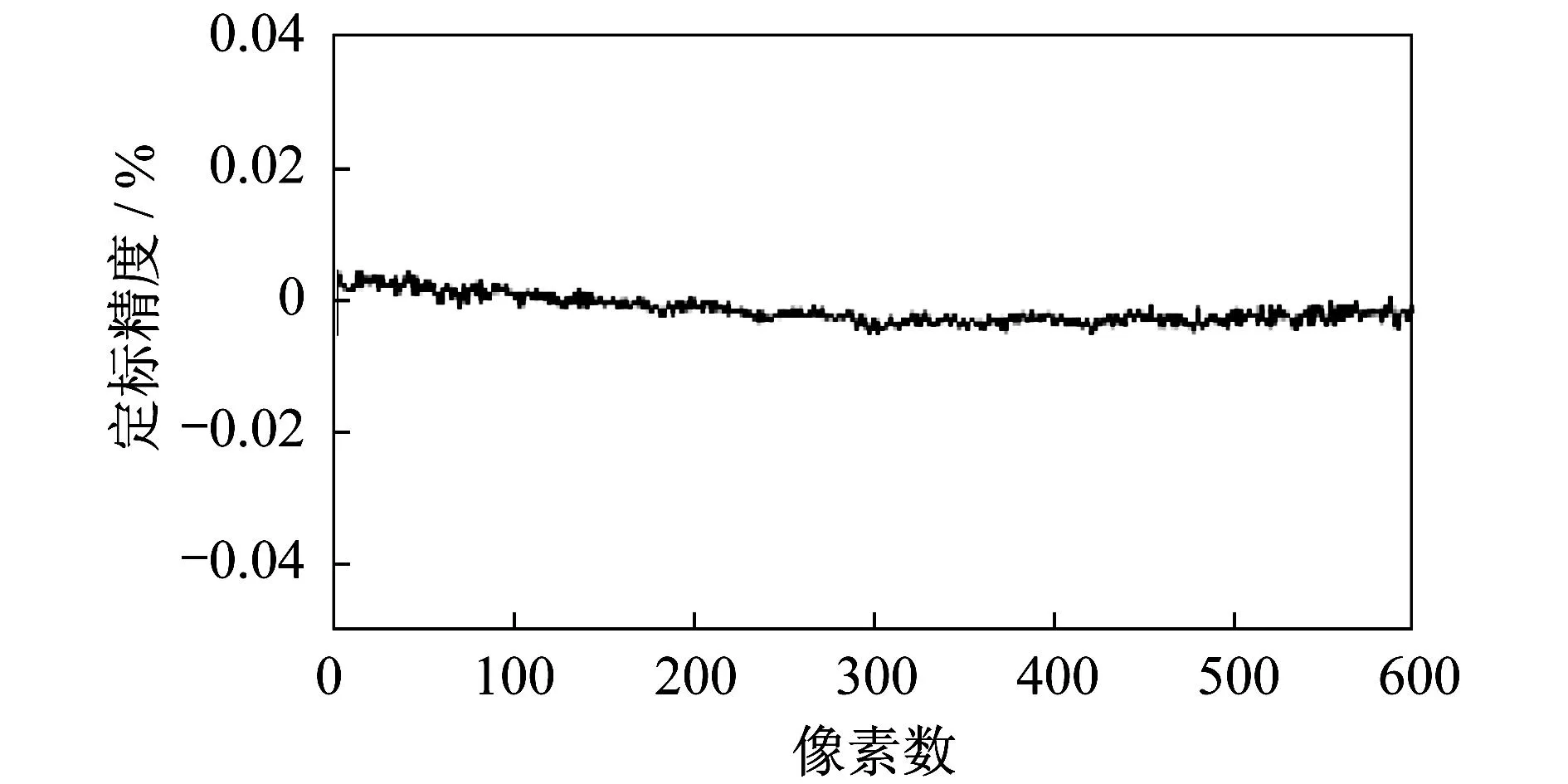
圖6　S/N=100 dB時像面響應度系數誤差

圖7　S/N=50 dB時像面響應度系數誤差

圖8　S/N=25 dB時像面響應度系數誤差

3非均勻照明平場定標過程

采用第一節中推導的最小二乘法迭代求解模型進行空間相機的平場定標,擺脫了對均勻照明條件的依賴,具有以下優點: 1) 降低了對試驗條件的要求,試驗的可操作性和成本優勢改進明顯; 2) 定標精度不再受照明均勻性的限制,能夠實現超高精度的平場定標; 3) 可以直接使用成像目標進行平場定標,非常適合空間相機的在軌定標; 4) 可用于真空紫外等短波波段光學儀器的平場定標。這些特點使得該方法具有巨大應用價值。

非均勻照明平場定標即可以進行CCD部件級別的平場定標,也適用于整機平場定標。CCD部件級別的平場定標流程如下:

(1) 點亮CCD照明光源并調節亮度,使得CCD曝光不飽和;

(2) CCD通過精密平移臺在兩維方向以數個像元距離等間距平移,并拍攝圖像;

(3) 平場求解模型需要以像元精度知道目標在像面上平移間距,此平移量可以通過使用高精度平移臺來獲取,也可以通過目標識別的圖像處理算法得到,后者更為實用;

(4) 采用第2節中編寫的求解模型程序處理所有目標圖像數據,得到CCD的響應系數分布函數。

整機平場定標過程有些不同,需要相機轉動改變光軸方向來實現目標在像面上的移動,具體流程如下:

(1) 相機固定在一個方位、俯仰兩維轉動平臺上,調整成像目標使得兩者正對;

(2) 調整成像目標亮度,使得相機成像不飽和;

(3) 相機正對成像目標成像,轉動平臺方位、俯仰,使得目標成像在像面不同位置;

(4) 采用目標識別算法處理所有目標移動圖像,獲取每幅圖像中目標的移動量;

(5) 采用相機像面響應度迭代求解模型,依據所獲得的圖像數據反演計算出相機的像面響應度系數分布,即完成平場定標。

4結論

本文在總結現有空間相機平場定標技術的基礎上,針對其存在的依賴均勻照明條件等問題,提出一種不需要均勻照明的平場定標方法,詳細介紹該方法的使用原理,并編程進行仿真驗證測試。測試結果表明該方法可以實現較高精度的平場定標,最后給出該平場定標方法在實際應用中的操作流程。

參考文獻：

[1]MACKAY C D.Charge-coupled devices in astronomy[J].Annual Reviews of Astronomy and Astrophysics,1986,24(1):255-283.

[2]BERRY R,BURNELL J.The handbook of astronomical image processing [M].2nd ed.Richmond,Va:Willmann-Bell,2005.

[3]江孝國,張開志,李成剛,等.圖像平場校正方法的擴展應用研究[J].光子學報,2007,36(9):1587-1590.

[4]邢進,王淑榮,李福田.空間紫外遙感光譜輻射計光譜輻亮度定標三種方法的比較[J].中國激光,2006,33(4):509-515.

[5]HEATH D F,WEI Z Y,FOWLER W K,et al.Comparison of spectral radiance calibrations of SBUV-2 satellite ozone monitoring instruments using integrating sphere and flat-plate diffuser techniques [J].Metrologia,1993,30(4):259-264.

[6]周勝利.積分球在實驗室內用于空間遙感器的輻射定標[J].航天返回與遙感,1998,19(1):29-34.

[7]夏果,周海洋,劉康,等.反射積分球建模及分析[J].光學儀器,2013,35(4):1-5,11.

[8]BARNES W L,PAGANO T S,SALOMONSON V V.Prelaunch characteristics of the Moderate Resolution Imaging Spectroradiometer(MODIS) on EOS-AM1 [J].IEEE,Transactions on Geoscience and Remote Sensing,1998,36(4):1088-1100.

[9]吳國棟,張曉輝,韓昌元,等.空間CCD相機輻射標定方法的應用研究[J].測試技術學報,2004,18(4):325-329.

(編輯:程愛婕)

A flat field calibration method of space camera based on a non-uniform target

YUEJinying1,LISuwen1,HELingping2

(1.College of Science,Changchun Institute of Technology, Changchun 130021, China;2.Changchun Institute of Optics,Fine Mechanics and Physics,Chinese Academy of Sciences, Changchun 130033, China)

Abstract：Flat field calibration is an essential calibration project for space camera. At present the uniform illumination target is generally used to fulfill space camera′s flat field calibration, but this method is limited in application because it relies on the uniformity of the target. A new flat field calibration method was proposed based on the non-uniform target. This method has a great practical value as it is no longer dependent on the uniform target. At first, a responsivity distribution calculation model of the camera image plane was established based on the pixels gray correlation of multiple non-uniform target images. Then by using the least-squares iteration method, the calculation model was solved. Meanwhile, a simulation program had been developed to test this calibration method. The test results show that the new calibration method′s precision is better than 0.5% when the image signal-to-noise ratio is higher than 25 dB. Finally, based on the characteristics of this method, a practical calibration process has been proposed.

Keywords：flat field calibration; non-uniform illumination; space camera; model simulation

中圖分類號：O 432.1

文獻標志碼：A

doi：10.3969/j.issn.1005-5630.2016.01.008

作者簡介：岳巾英(1983—),女,實驗師,主要從事光學設計、光學檢測等方面的研究。E-mail:yuejy444@163.com通信作者： 何玲平(1982—),男,副研究員,主要從事短波光學、光學檢測等方面的研究。E-mail:hlp200201@163.com

基金項目：國家自然科學基金(NSFC 11304021)

收稿日期：2015-05-11