邏輯系統外的“真”

梅祥

（華東政法大學人文學院，上海201620）

邏輯系統外的“真”

梅祥

（華東政法大學人文學院，上海201620）

非形式論證有廣義與狹義之分，在一個形式邏輯系統外非形式論證應做狹義理解，即不可能前提真并且結論假。而在一個形式邏輯內的可靠性證明中就蘊涵了這種狹義的非形式論證。因此，一個邏輯系統只要證明它是可靠的，那么它就能保證不可能前提真并且結論假的出現。

系統外的有效性； 非形式論證； 可靠性證明

邏輯系統外的“真”是什么呢？說到邏輯系統外，人們都會想到非形式論證，而非形式論證我們不能簡單地講述它，而是應該將其作廣義與狹義之分。一個形式邏輯系統只與狹義的非形式論證發生密切聯系，而廣義的非形式論證更多應用于修辭學與論辯學。這里講的邏輯系統外便指的是狹義的非形式論證，而它的“真”便正是系統外的有效性，即不可能前提真并且結論假。那么如何來保證這種邏輯系統外的“真”呢？本文將著力分析。

一、形式邏輯與非形式邏輯

形式邏輯與非形式邏輯之間的主要區別表現在以下三個方面：首先，形式邏輯和非形式邏輯研究的論證類型不同。語言是描述世界的一種載體，論證是確定對世界認知的一種方式。語言和論證相輔相成，論證的展開離不開語言，通過語言帶給我們交流和溝通的價值來自于論證。沒有語言，論證失去了它存在的基礎；沒有論證，語言失去了它應有的可信度。而語言又往往被劃分為自然語言和形式語言。自然語言又被稱為日常語言，是我們日常生活和工作中正常使用的用來溝通和交流的語言，通常它很直觀、形象、易理解，但往往由于它缺乏精確性，從而導致語言歧義現象比較多。形式語言又被稱為符號語言，是我們從自然語言中抽象出來內容，保留語言的語形，只從語言結構上來研究和使用語言。形式語言雖然缺乏直觀、難理解，但由于它舍棄了內容，所以能夠避開一些自然語言中帶來的語言歧義，使得語言本身更加精確。形式邏輯使用的語言是符號語言，基于它自身的精確性和結構化，往往被用來設計邏輯系統，進行形式論證。非形式邏輯使用的是自然語言，基于它自身符合日常直觀，往往被用來進行非形式論證，目的是為了說服目標聽眾。兩種語言各有自身的優缺點，關鍵在于我們的使用。

如果我們從論證的角度做區分，形式論證勢必需要依賴形式邏輯，比如對一個命題表達式做出有效判定需要依賴不同形式邏輯系統的邏輯規則，形式邏輯是進行形式論證的必要工具。而非形式論證并不必然需要依賴形式邏輯。雖然因為缺乏形式邏輯，使得非形式論證在論證的精確性上無法與形式論證相比擬，但是非形式論證的目的在于說服聽眾，所以自然語言的直觀性更加符合非形式論證的目的。所以非形式論證更需要借助非形式邏輯，而非形式邏輯。

其次，研究論證的維度不同。在對語言的研究過程中，人們往往會從語形、語義和語用三個方面對語言展開研究。邏輯學家基于上述三個方面的研究，由此產生了邏輯語形學、邏輯語義學和邏輯語用學。邏輯語形學一般研究邏輯系統，主要是研究形式邏輯語言基于相應的邏輯規則給出有序的排列；邏輯語義學一般研究形式化邏輯語言中的真之問題，其中包括對真之定義、可滿足、指派等問題的研究。上述兩種邏輯研究主要采用的是形式化的語言，所以它們都是依賴于形式邏輯。雖然邏輯語形學和語義學對于邏輯的發展意義重大，但由于它在一定程度上脫離了我們的日常語言，忽略了語言使用的語境因素，導致了這種研究方式有時違背了我們日常對語言的直覺性的使用，比如塔爾斯基對真這個概念所做的語言層級的劃分。而邏輯語用學關注的是邏輯語言在不同的語言環境下的使用，它使我們的邏輯語言不再是停留在紙面上的公理和定理，它需要我們去考慮語境，根據語境的不同考察邏輯語言的正確使用。因為邏輯語用學考慮到了語境，所以這就需要我們考慮語言中的內容，而不再僅僅是語言的框架和結構。因而基于邏輯語用學，以自然語言論證為研究對象的非形式邏輯、語用論辯術等以非形式論證為研究對象的理論應運而生。

第三，形式邏輯是研究論證形式的,非形式邏輯是研究論證結構的。如果我們從微觀和宏觀的角度來對論證做區分，那么形式邏輯往往就會從微觀來研究論證的形式，而非形式邏輯往往就會從宏觀來研究論證的結構。從形式上來看，一個形式論證是否有效取決于該形式論證是否符合相應邏輯系統的邏輯規則。比如在命題邏輯中，一個論證形式“如果天下雨，那么地是濕的，天是下雨的，所以地是濕的”，我們用P代表“天下雨”，S代表“地是濕的”，那么這個論證形式可以寫成“（P→S）∧P→S”。我們知道這一論證形式之所以有效是因為它是我們命題邏輯里的MP規則，而MP規則是符合我們的直觀。再比如，對于論證“所有法是人類一定意志的體現；刑法是法；所以，刑法是人類一定意志的體現。”我們用S代表“法”，P代表“人類一定意志的體現”，a代表“刑法”，上述論證形式便可以改寫為：所有S是P；a是S；因此，a是P。如果從謂詞邏輯來看，我們可以把它修改為：（x）（Sx→Px），Sa，所以Pa。顯然，無論是根據傳統邏輯中三段論的規則，還是根據謂詞邏輯的規則，這個論證都是有效的。

然而，一個添加了具體內容考慮語境的非形式論證，往往考慮的情況要比單獨依賴于形式邏輯技術的形式論證復雜得多。由于形式邏輯只考慮形式，不考慮內容。所以對于結論所依賴的前提，形式邏輯往往只考慮前提與前提之間，前提與結論之間的形式關系，并不考慮它們是具體如何互相支持的。但在日常人們對語言的使用中，前提之間、前提與結論之間的具體關系是人們使用語言必不可少要考慮的因素。而非形式邏輯則研究這些內容，并形成了對其中四種情況的研究，即一個前提是如何獲得另一個前提的支持、兩個或兩個以上的前提如何獨立得出同一個結論、兩個或兩個以上的前提如何共同得出同一個結論、兩個或兩個以上的結論如何共同從一個前提得出。

二、形式論證與非形式論證

形式論證是指以形式語言（人工語言）為論證載體，基于系統內的有效性對一個邏輯系統內部所進行的推理。形式論證是非直覺的，是形式化的，它從一個系統內的有效性中研究論證形式。而這一有效性又可以分為語形有效性和語義有效性。哈克在《邏輯哲學》中對此做了詳細解釋：“我將把一個形式論證表示為合式公式組成的一個序列（即一個形式語言的合語法語句，以下叫做‘合式公式’（wffs）） A1…An-1，An，（n≥1），其中A1……An-1是前提，An是結論。這樣一來，語形的有效性就能解釋如下：

A1……An-1，An在L中是有效的，僅當An通過L的推理規則，可以從A1……An-1和L中的公理（如果有的話）中推出。這通常表示為：A1……An-1├LAn。

語義的有效性可解釋如下：

A1……An-1，An在L中是有效的，僅當在A1……An-1是真的一切解釋中，An都是真的。這通常表示為：A1……An-1LAn。‘├L’和‘L’中的L用來提醒人們注意，有效性的這兩個概念都是相對于系統而言的。”[1]24那么對于一個邏輯系統的證成標準則是通過可靠性和完全性來實現的。“根據可靠性，這個系統不會出現矛盾，因為如果有矛盾的話，就不會都是真的；根據完全性，這個系統就包括了所有的真命題，而且這些真命題之間具有推出關系。”[2]80因此，在形式論證中必須考慮可靠性和完全性。

我們在日常生活中對一論證進行判斷通常都是靠直觀，而并非像邏輯學家那樣進行復雜的邏輯形式推理。雖然我們的這樣的非形式化判斷的直覺性很強，但通常都能為我們的經驗所承載。我們把這一利用非形式語言（自然語言）作為論證載體，基于系統外的有效性，對一個邏輯系統進行直觀的判斷的論證形式稱為非形式論證。對于非形式論證的研究是美國當代著名的傳統邏輯學家柯庇等人把它引入到邏輯學的視野范圍之內，而非形式邏輯學家福柯林和產諾特—阿姆斯特朗則把對非形式論證的研究推向了一個新的高潮。福柯林他們認為論證除了需要關注語形、語義，還需要關注論證評價的語用要素—語境，如：論證參與者、相干性、可接受性、目標聽眾等。正因為如此，我認為他們對于非形式論證的研究更多適用于修辭學與論辯學，而非邏輯學。所以，他們用“好”與“壞”來分別取代“有效”與“無效”。因此，考慮到語境概念的非形式論證是一種更廣泛意義上的非形式論證，而我更贊同前面所述通過系統外的有效性進行直觀判斷的非形式論證，在此我稱之為狹義的非形式論證。哈克在講到這種系統外的有效性時是這樣解釋的：“如果一個論證的前提是不可能的，或者如果它的結論是必然的，那么由于更不可能前提真‘并且’結論假，因而這個論證是有效的；當然，情況是如此，即使前提對結論毫不相干。”[1]28因此哈克對于非形式論證的看法是其結論得自它的前提，即它不可能前提真并且結論是假的[1]25。在這一點上我是贊同的。因此我們在對一個邏輯系統進行非形式論證時只需要直觀地去判斷它不可能前提真并且結論假就能證明它是有效的，而不需要再去考察它的相關性、可接受性等修辭學概念。哈克認為這些屬于修辭學的范疇，不屬于論證評價的邏輯范疇[1]28。把相關性、可接受性等放入修辭學中我認為是恰當的。因為每個人可接受的標準、對事物相關的看法是不一致的，是不同經驗塑造的，真理也不是因為人們能不能去接受它而存在，它是客觀的。如果把這些放入到一個論證評價的邏輯系統中去，則會導致適用不確定性去評價穩定性，這是不可靠的，也無法讓我們從直觀上看到真理。雖說是非形式論證，是我們日常直覺的判斷，但我們同樣需要保證它的正確性與一致性。而使用狹義的解釋，即我們用實例代入一個邏輯系統中不可能出現前提真并且結論假的情況，我們便說它是有效的，是成功的，便能讓我們直觀的判斷做到這一點。

三、可靠性證明保證了邏輯系統外的“真”

既然依前所述，在一個邏輯系統外，非形式論證應做狹義解釋，只要非形式論證的結論得自它的前提，即它不可能前提是真并且結論是假的，我們就說它在系統外是有效的，那么在系統內我們去證明這個邏輯系統是可靠的和完全的就足夠了，不需要再有一個正確性的問題。（陳波老師在他的《邏輯哲學》中提到了一個正確性的問題[3]60） 因為我們在證明一個邏輯系統的可靠性時就已經從形式上蘊涵著不可能前提真并且結論假。我們先以一個被廣泛使用的一階邏輯系統PL1為例來證明一個邏輯系統的可靠性。PL1的初始聯結詞是 ┐和→，其解釋由下面的真值表給出，其中“T”代表“真”，“F”代表“假”：

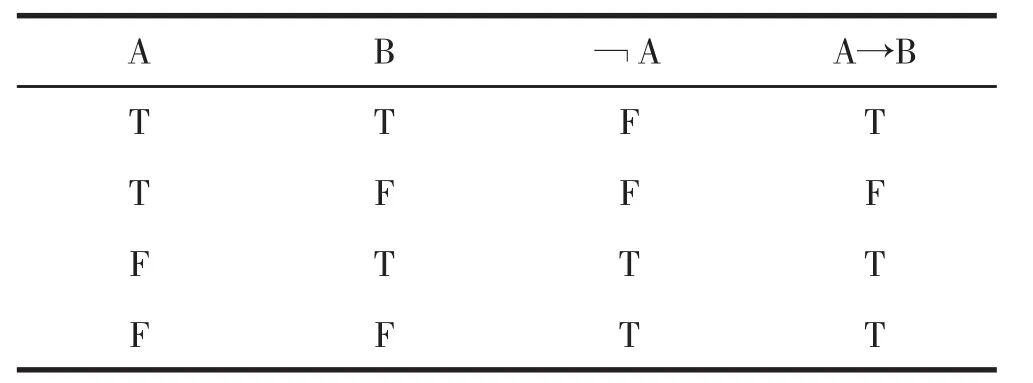
表1 真值表

并通過下述定義引進其他的聯結詞：

2.（A∨B）=df（┐A→B）。

PL1的其他構成如下：

公理1.A→（B→A）。

2.（A→（B→C））→（（A→B）→（A→C））。

變形規則

MP（肯定前件規則）從A→B和A推出B。

證明：設A真并且A→B真。根據→的真值表，如果A真并且A→B真，則B真。所以，B真。

這樣我們就證明了PL1的可靠性。正如上述在進行PL1的可靠性證明過程中，其公理和變形規則都要通過真值表得到保真性的驗證，即不可能前提真并且結論假的情況的出現，所以它就在此確保了整個邏輯系統即使以實例代入進來，人們再去用非形式論證的視角去考驗時也不會有前提真并且結論假的情況的出現，而真值表是人們抽象出的客觀世界經過人們的思維去內容化后所體現的在一個系統中的形式“真”，這是值得人們信賴的。所以在一個邏輯系統的可靠性的證明過程中就保證了無論是形式還是非形式下的對邏輯系統的論證評價。至于陳波老師舉出的邏輯萬能原則與道義邏輯系統的例子[3]60，我認為這是基于每個人的理解不一致所導致的，而不能放到對一個邏輯系統的論證評價中去。只要這些定理在該系統的可靠性證明過程中具有保真性，那么我們再以實例代入時，就不會出現前提真并且結論假的情況。如果出現，那么只有兩種情況：要么該邏輯系統不可靠；要么是對公理或者定理的理解不正確。比如以道義邏輯系統中OP→P為例，它意味著：如果P是義務的，則P就是現實的；換句話說，一切應該做的事情實際上都做了[3]60。在陳波老師對OP→P的釋意中，在“換句話說”的前一句我是贊同的，后面一句我認為更應該這樣理解：換句話說，一切應該做的事情都是義務，而義務不一定就是實際上都做了。這些事情既然已為道義所確定，那么它就相應地讓每個人都背負著它而生存，如果你不去做這些應該做的事情，你將會受到來自道德、法律或者宗教等的懲罰，這種懲罰也許是肉體上的，也許是心靈上的，但無論如何，你不去做應該做的事而來自于道義上的懲罰便印證了它的存在。因此OP→P在形式上是可靠的并且完全的，在一個道德現實世界中它也是一個正確的邏輯。

四、結語

陳波老師認為，只有具備哲學關懷的邏輯學家才會注意到邏輯是非純形式的，非無內容的（對于這一觀點的不同意見可參見王路老師寫的《邏輯真理是可錯的嗎？》[4]），才會注意到一個邏輯系統的證成，除需要證明可靠性、完全性外還需要有正確性問題，即是否還符合我們所居住的這個現實世界[3]60-61。在此，我需要講的是，我們的形式邏輯確實需要符合我們所居住的這個現實世界，但通過上述分析，我們知道形式邏輯需要反映、需要符合的是這個現實世界中客觀存在的規律，在我看來就是不可能前提真并且結論假，狹義的非形式論證也正是通過直觀的方式揭示了這一點，而不是去符合、去反映人們大腦中對這個現實世界所接受、所理解的樣式。在證明一個邏輯系統的可靠性時就已經能證明這一點了。因此如果能證明一個邏輯系統是可靠的和完全的，主要是它的可靠性，那么它就是成功的，從而它也能夠實現確保邏輯系統外的“真”了。

[1][英]蘇珊·哈克著.邏輯哲學[M].羅毅譯.北京：商務印書館，2006.

[2]何向東主編.邏輯與方法導論[M].重慶：重慶出版社，2006.

[3]陳波著.邏輯哲學[M].北京：北京大學出版社，2005.

[4]王路.邏輯真理是可錯的嗎？[J].哲學研究，2007（10）：108.

The“Truth”beyond Logical System

MEI Xiang
（East China University of Political Science and Law，Shanghai 201620）

The term“informal argument”can be used in a broad and a narrow proof.Informal argument should be used in a narrow sense when it is not in the formal logical system，namely，it is impossible that premise is true and conclusion is false.And such kind of informal argument with narrow sense can be contained in a reliable proof in the formal logic.Therefore，if the logical system can be proved as reliable，then it ensures the circs of premise is true and conclusion is that false cannot be set up.

effectiveness beyond system； informal argument； reliable proof

B085

A

1671－9743（2016）10－0038－03

2016-09-19

上海市優秀青年教師資助培養項目（A-4906-16-00607）；中國博士后科學基金（2014M560999）。

梅 祥，男，講師，博士，清華大學人文學院博士后，研究方向：邏輯學，法學。