改進的加權支持向量機回歸的諧波發射水平估計方法

邱思語　楊洪耕

(四川大學電氣信息學院　成都　610065)

?

改進的加權支持向量機回歸的諧波發射水平估計方法

邱思語楊洪耕

(四川大學電氣信息學院成都610065)

摘要提出一種利用改進的加權支持向量機回歸估計系統諧波阻抗及諧波發射水平的新方法。根據公共連接點處諧波測量數據的差異，利用歐幾里德距離作為加權指標修正支持向量機的誤差要求，通過線性插值確定懲罰參數的加權參數，以此形成用于估計系統諧波阻抗的加權支持向量機回歸模型，從而求解諧波發射水平。通過對仿真電路的理論分析和現場數據的實際應用，證明了所提方法能有效抑制背景諧波波動對估計結果的影響。

關鍵詞：諧波阻抗諧波發射水平加權支持向量機回歸

Assessment Method of Harmonic Emission Level Based on the Improved Weighted Support Vector Machine Regression

QiuSiyuYangHonggeng

(School of Electrical Engineering & InformationSichuan UniversityChengdu610065China)

AbstractThis paper proposes a new method to estimate the system harmonic impedance and the harmonic emission level based on the improved weighted support vector machine (WSVM) regression.According to the differences of harmonic measurement data at the point of common coupling，the WSVM can be obtained by correcting the error requirement of SVM by using Euclidean distance as a weighted index and determining the weighted coefficient of the penalty parameter by linear interpolation.Then the system harmonic impedance and the harmonic emission level can be calculated.Based on analyzing the simulation of the circuit and the practical application of field data，it proves that the proposed method can effectively restrain the influences caused by the fluctuation of the background harmonics on the estimation results.

Keywords：Harmonic impedance，harmonic emission level，weighted，support vector machine，regression

0引言

當今電網在飛速發展的同時，也帶來了許多急需解決的問題。其中，大規模的非線性和沖擊性負荷在接入電網后產生了嚴重的電力諧波污染問題。準確地估計用戶側和系統側的諧波發射水平對PCC點(公共連接點)的諧波污染責任分割起著至關重要的作用[1-6]。而評估諧波發射水平的難點在于如何在系統參數和電網運行方式不斷變化的情況下準確地估計系統諧波阻抗[7-13]。

系統諧波阻抗估計方法主要分為“干預式”和“非干預式”兩類。“干預式”方法利用向電網注入諧波/間諧波電流或者某條支路的開斷來估計諧波阻抗，這種外界的干預可能影響電力系統的正常運行狀態，不能廣泛使用。“非干預式”方法則是圍繞可測得的PCC點諧波數據進行研究，從已知數據中挖掘和提取諧波阻抗信息，主要包括：①波動量法[1]，考慮背景諧波波動較小時系統諧波阻抗可近似由PCC點諧波電壓和電流波動量的比值代替，簡單實用，因此被廣泛應用。但該方法要求測量參數具有較高的準確性且背景諧波基本保持穩定；②回歸法[8-10]，根據電力系統等效電路推導出回歸方程，并將回歸方程中的截距項視作恒定，從而將諧波阻抗的求解轉換為回歸系數的求解，但該方法也要求背景諧波基本保持穩定以滿足回歸假設，否則回歸方程將失去原有的穩健性；③隨機獨立矢量法[11]，考慮實際電網中PCC點諧波電流受背景諧波影響較小，以獨立隨機矢量協方差為零的思想建立模型，推導出諧波阻抗的估計公式，在一定程度上削弱了背景諧波波動的干擾，但其要求諧波電流的波動由用戶側主導，諧波電壓的波動由雙方共同主導，當系統波動不符合上述要求時，該方法計算結果值得進一步商榷；④支持向量機法[13]，通過結構風險最小化原理提高泛化能力，較好地解決了小樣本、非線性、高維數、局部極小點等實際問題，已在模式識別、信號處理和函數逼近等領域得到了應用。文獻[13]以PCC點諧波數據作為輸入，利用支持向量回歸機回歸估計諧波阻抗，由于二次規劃的解是全局最優且惟一的，因此該方法具有較好的估計精度和泛化性，但該文中并未根據支持向量樣本對訓練結果的影響提出模糊隸屬度，忽略了支持向量樣本個體間的差異，即未考慮背景諧波波動造成的諧波測量數據的差異對阻抗估計結果的影響，估計結果可能偏離真實值。

基于現有支持向量機法計算系統側諧波阻抗的不足，本文提出基于改進的加權支持向量機方法[17，18]的諧波阻抗估計方法，提出以權參數衡量諧波樣本間的差異性，從而修正回歸模型中的懲罰參數和誤差要求，達到抑制背景諧波波動的效果。對理論進行仿真計算并通過現場數據驗證，證明該方法能有效抑制背景諧波的影響。

1支持向量機法

電力系統諧波分析的等效電路模型如圖1所示。其中，Is和Zs分別為系統側某次諧波的等效電流源和諧波阻抗；Ic和Zc分別為用戶側某次諧波的等效電流源和諧波阻抗；UPCC和IPCC分別為PCC點的某次諧波電壓和電流，為測量所得數據。

圖1　系統側和用戶側等效電路Fig.1　Norton equivalent of the utility and customer

根據電路原理，可推導出

UPCC=IPCCZs+IsZs

(1)

UPCC=-IPCCZc+IcZc

(2)

將式(1)、式(2)整理后可得

(3)

(4)

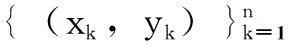
在采用支持向量機構造回歸估計函數時，通常轉換為構造并求解凸二次規劃問題。

(5)

在上述二次規劃問題中，誤差要求ε和懲罰參數C的選取是影響支持向量機回歸結果的關鍵。ε表示回歸模型對訓練樣本誤差的要求，ε值越小意味著對模型回歸精度的要求越高，解得的回歸函數精度也越高。懲罰參數C表示對超出誤差要求ε的樣本數據的懲罰，C值越小意味著對超出誤差要求的樣本懲罰力度就越小，從而增大訓練誤差[17，18]。在文獻[13]采用的支持向量機方法中，回歸模型需在一開始確定誤差要求ε和懲罰參數C的值，且在之后的計算中保持不變，即對于所有的諧波數據，其誤差要求及超出誤差要求的懲罰一樣。但實際在計算系統諧波阻抗時，考慮背景諧波波動的影響，不同時刻PCC點的諧波電壓和諧波電流對估計諧波阻抗的重要性有所不同，受背景諧波波動影響越小的數據重要性越大，針對不同重要性的諧波樣本應選擇不同的誤差要求和懲罰參數加以約束，從而減少重要性小的諧波數據對阻抗估計的影響。因此，本文提出采用改進的加權支持向量機回歸[17，18]計算系統側諧波阻抗。

2改進的加權支持向量機回歸的諧波阻抗及諧波發射水平估計方法

2.1基本原理

在加權支持向量機中，首先應量化樣本的重要性，然后以樣本的重要性作為加權指標確定每個樣本的誤差要求ε和懲罰參數C的加權參數ti和si[17，18]。為了量化各樣本數據的重要性，本文采用歐幾里德距離作為量化指標，計算測試樣本與各訓練樣本的距離，并按距離大小將訓練樣本重新排序。歐幾里德距離越短，樣本重要性越大，懲罰參數C的權參數si越大，誤差要求ε的權參數ti越小。基于上述分析，最重要樣本(距離最短樣本)的權參數si應取最大值，ti應取最小值，故令si=1，ti=0.01；而最不重要樣本(距離最遠樣本)的權參數si應取最小值，ti應取最大值，故令si=0.01，ti=1[17]。經多次實驗驗證，利用兩種極端情況下的樣本參數，通過線性插值計算其余樣本的權參數[17]。

權參數ti和si確定后，原有的誤差要求ε和懲罰參數C也相應地改變為εti和Csi，式(5)的凸二次規劃問題即轉換為

(6)

求解式(6)的凸二次規劃問題即可得到拉格朗日乘子

（CRISPR）－Cas9是當下熱門的基因編輯技術，但無法對細胞器中基因進行編輯。而PPR家族蛋白具備進入細胞器中與單鏈RNA結合的能力，并且識別結合RNA 4種核苷酸的部分PPR基序特點已被研究證實，還有更多的識別密碼正在被研究和驗證。在此基礎上，針對靶標RNA單鏈序列特征，人工設計對應的PPR蛋白，通過融合相應的功能結構域，人工設計融合的PPR蛋白有望成為能夠調控細胞器基因表達的新一代生物技術。

(7)

從而構造回歸估計函數

(8)

(9)

(10)

2.2系統側諧波阻抗及諧波發射水平估計

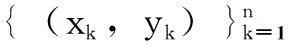
圖2　加權支持向量機估計Zs步驟Fig.2　The steps of the Zs estimation by weighted support vector machine

回歸得到諧波阻抗Zs后即可求解用戶側諧波電壓發射水平

Uc-PCC=IPCCZs

(11)

從而可得到系統側諧波電壓發射水平

Us-PCC=IsZs=UPCC-Uc-PCC

(12)

3仿真實驗

根據圖1所示系統側和用戶側等效電路，用Matlab按照文獻[11]的仿真模型生成數據，等效電路的對應參數設計如下：

1)Ic幅值初始值為143.93 A，Ic的相角恒為0°，對Ic的幅值加上±20%的隨機波動。

2)Is幅值初始值為Ic的k倍，其中k可取0.1、0.4、0.7、1.0、1.3、1.5，Is相角初始值為60°，對Is的幅值加上±5%的隨機波動，對Is的相角加上20%的正弦波動。

4)Zs幅值初始值為0.101 76 Ω，加上20%正弦波動；Zs相角初始值為70°，加上10%正弦波動。

利用上述等效電路仿真模型隨機生成10 000組樣本數據，按每60組樣本數據分段進行遞推計算，利用本文方法(方法4)進行系統諧波阻抗及諧波發射水平的估計，同時與二元回歸法[9](方法1)、支持向量機法[13](方法2)及獨立隨機矢量法[11](方法3)進行比對，結果見表1及表2。

k平均誤差(%)(理論值0.1147Ω)方法1方法2方法3方法40.10.940.110.090.070.41.130.150.170.090.71.870.180.210.121.09.100.670.740.141.316.890.850.960.171.520.041.742.820.25

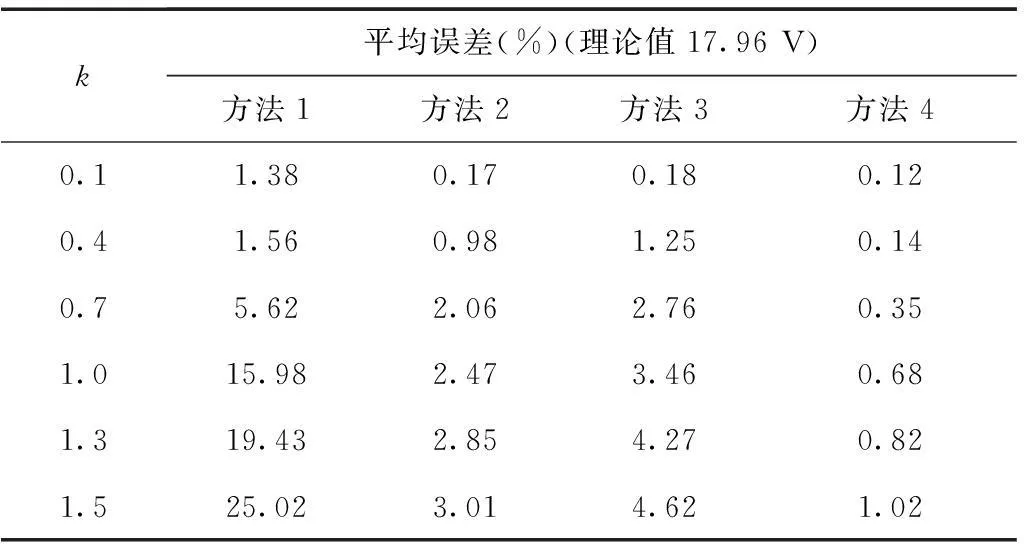
表2　Uc-PCC 95%概率值估計誤差

k的取值代表不同的背景諧波波動情況，從表1、表2可看出，隨著k值的增加，4種方法的計算誤差均呈不同程度的增長趨勢，而本文方法的計算誤差增長趨勢最小，隨著k值的變化基本保持穩定，證明本文方法具有更好的計算穩定性。而在相同背景諧波波動情況下，本文方法的計算結果誤差最小，最接近真實值，具有更高的計算精度。而在計算速度方面，不同的測試樣本需要重新計算樣本權參數，并重新進行訓練，在訓練樣本數量不多時，計算速度與傳統方法差異并不明顯；而在訓練樣本數量巨大時，可以丟棄那些空間距離較遠的訓練樣本，只保留數量較少的訓練樣本，以減少樣本的訓練時間。

4實測數據計算

本文采用現場實測數據進一步對所提方法的有效性和準確性進行驗證。實際測量數據來自一100 MV·A的工業直流電弧爐的150 kV母線，系統短路容量為7 500 Mvar。測量數據由LEM TOPAS 1000系列電能分析儀以6 400 Hz的采樣頻率測得。圖3為PCC點測得的某日連續10 h內的3次諧波電壓和電流幅值。

圖3　PCC點3次諧波電壓和電流幅值Fig.3　Magnitude waveforms of the 3rd harmonic voltage and current at the PCC

分別利用上述4種方法對實測3次諧波數據按60 min分段計算系統諧波阻抗，計算結果如圖4所示。

圖4　系統3次諧波阻抗幅值和相角Fig.4　The 3rd harmonic impedance magnitudes and angles of Zs

分析圖4可知，方法1(二元回歸法)利用最小二乘法回歸估計諧波阻抗，回歸方程中的截距會隨背景諧波波動而變化，從而使回歸法失去原有的穩健性，導致阻抗估計結果波動較大；方法2(支持向量機法)利用支持向量機回歸求解諧波阻抗，由于其解是全局最優且惟一的，具有較好的精度，但其未考慮背景諧波波動造成樣本差異的問題，導致支持向量機的回歸估計在局部偏離真實值；方法3(獨立隨機矢量法)利用PCC點諧波電流與背景諧波的弱相關性推導出諧波阻抗的估計公式，有效抑制了背景諧波波動的影響，估計結果較為平穩；方法4(本文方法)利用對誤差要求和懲罰參數C加權的思想解決了方法2存在的問題，估計結果有明顯改善，與方法3相比，估計結果更為平滑，且通過第3節仿真實驗分析，能更好地抑制背景諧波波動的影響，具有更好的精度和穩定性。

最后，通過已求得的系統諧波阻抗計算PCC點用戶側和系統側諧波電壓發射水平，得到的發射水平95%概率值如表3所示。利用停機運行時的3次諧波電壓作為系統側諧波電壓發射水平的真實值，如圖5所示，并計算95%概率值為212.46 V。與表3數據相比，進一步驗證了本文方法的準確性和有效性。

表3　用戶側和系統側諧波電壓發射水平95%概率值

圖5　停機1 h的3次諧波電壓幅值Fig.5　The 3rd harmonic voltage amplitude in a shutdown hour

5結論

本文方法在計算系統諧波阻抗時，利用諧波測量數據的差異對支持向量機的誤差要求和懲罰參數C加權，抑制了背景諧波波動對阻抗估計結果的影響。仿真電路的計算和現場實測數據的分析均證明了本文所提方法的準確性和有效性，具有很好的理論研究價值和工程應用前景。

在加權支持向量機中，每更換一次測試樣本，樣本權參數則需要重新計算，并重新進行訓練，計算量大，計算速度慢。因此，這種加權支持向量機方法一般適用于離線計算或對實時性要求不高的場合。在樣本數量巨大時，丟棄一些重要性指標較低的訓練樣本，可減少訓練時間及訓練計算量。

參考文獻

[1]Yang H，Pirotte P，Robert A.Harmonic emission levels of industrial loads statistical assessment[C]//CIGRE Proceedings：International Council on Large Electric Systems，Paris，1996：456-462.

[2]Xu Wilsun，Liu Yilu.A method for determining customer and utility harmonic contribution at the point of common coupling[J].IEEE Transactions on Power Delivery，2000，15(2)：804-811.

[3]Xu Wilsun，Ahmed E E，Zhang Xiqin，et al.Measurement of network harmonic impedances：practical implementation issues and their solutions[J].IEEE Transactions on Power Delivery，2002，17(1)：201-216.

[4]林海雪.公用電網諧波國標中的幾個問題[J].電網技術，2003，27(1)：65-70.

Lin Haixue.Some problems in national standard for harmonics in public supply network[J].Power system Technology，2003，27(1)：65-70.

[5]國家技術監督局.GB/T 14549—1993電能質量：公用電網諧波[S].北京：中國標準出版社，1993.

[6]劉秀玲，王洪瑞.電網諧波阻抗的測量及修正[J].電力系統及其自動化學報，2007，19(2)：55-58.

Liu Xiuling，Wang Hongrui.Measurement and correction of network harmonic impedances[J].Proceedings of CSU-EPSA，2007，19(2)：55-58.

[7]楊洪耕，王磊.基于拉蓋爾多項式的非線性負荷諧波發射水平估計[J].中國電機工程學報，2005，25(7)：81-85.

Yang Honggeng，Wang Lei.Assessing harmonic emission levels from non-loads using Laguerre polynomials[J].Proceedings of the CSEE，2005，25(7)：81-85.

[8]車權，楊洪耕.基于穩健回歸的諧波發射水平估計方法[J].中國電機工程學報，2004，24(4)：39-42.

Che Quan，Yang Honggeng.Assessing the harmonic emission level based on robust regression method[J].Proceedings of the CSEE，2004，24(4)：39-42.

[9]張巍，楊洪耕.基于二元線性回歸的諧波發射水平估計方法[J].中國電機工程學報，2004，24(6)：50-53.

Zhang Wei，Yang Honggeng.A method for assessing harmonic emission level based on binary linear regression[J].Proceedings of the CSEE，2004，24(6)：50-53.

[10]李麗，馬宏忠，姜寧，等.基于改進偏最小二乘法的系統諧波阻抗及諧波發射水平估算[J].電力系統保護與控制，2011，39(1)：92-95，131.

Li Li，Ma Hongzhong，Jiang Ning，et al.Assessing harmonic impedance and the harmonic emission level based on improved partial least-squares regression method[J].Power System Protection and Control，2011，39(1)：92-95，131.

[11]惠錦，楊洪耕，林順富，等.基于獨立隨機矢量協方差特性的諧波發射水平評估方法[J].電力系統自動化，2009，33(7)：27-31.

Hui Jin，Yang Honggeng，Lin Shunfu，et al.Assessment method of harmonic emission level based on covariance characteristic of random vectors[J].Automation of Electric Power Systems，2009，33(7)：27-31.

[12]龔華麟，肖先勇，劉亞梅，等.基于主導波動量篩選原理的用戶諧波發射水平估計方法[J].中國電機工程學報，2010，30(4)：22-27.

Gong Hualin，Xiao Xianyong，Liu Yamei，et al.A method for assessing customer harmonic emission level based on the dominant fluctuation filtering principle[J].Proceedings of the CSEE，2010，30(4)：22-27.

[13]康婕，解紹鋒，劉曉菊，等.基于支持向量機的諧波阻抗估計方法[J].電力系統保護與控制，2010，38(22)：131-134，205.

Kang Jie，Xie Shaofeng，Liu Xiaoju，et al.Assessing the harmonic impedance based on support vector machine[J].Power System Protection and Control，2010，38(22)：131-134，205.

[14]Vapnik V N.The Nature of Statistical Learning Theory[M].New York：Springer，1995.

[15]閻滿富，田英杰.改進的支持向量回歸機[J].系統工程，2004，22(10)：9-12.

Yan Manfu，Tian Yingjie.The improvement of support vector regression[J].Systems Engineering，2004，22(10)：9-12.

[16]杜樹新，吳鐵軍.用于回歸估計的支持向量機方法[J].系統仿真學報，2003，15(11)：1580-1586.

Du Shuxin，Wu Tiejun.Support vector machines for regression[J].Journal of System Simulation，2003，15(11)：1580-1586.

[17]杜樹新，吳鐵軍.回歸型加權支持向量機方法及其應用[J].浙江大學學報(工學版)，2004，38(3)：47-51.

Du Shuxin，Wu Tiejun.Weighted support vector machines for regression and its application[J].Journal of Zhejiang University(Engineering Science)，2004，38(3)：47-51.

[18]李忠浩，王宇.改進的加權型支持向量回歸方法[J].計算機輔助工程，2006，15(1)：31-33.

Li Zhonghao，Wang Yu.Improved weighted support vector regression[J].Computer Aided Engineering，2006，15(1)：31-33.

[19]鄧乃揚，田英杰.支持向量機—理論、算法與拓展[M].北京：科學出版社，2009.

邱思語男，1990年生，碩士研究生，研究方向為電力系統諧波分析與評估。

E-mail：412582182@qq.com(通信作者)

楊洪耕男，1949年生，教授，博士生導師，研究方向為電能質量分析與控制。

E-mail：pqlab99@126.com

作者簡介

中圖分類號：TM72

收稿日期2015-03-27改稿日期2015-10-08