基于RMA的三維成像與二維MIMO陣設計

王　武，陸必應，孫　鑫，周智敏(國防科技大學 電子科學與工程學院，　長沙 410073)

?

基于RMA的三維成像與二維MIMO陣設計

王武，陸必應，孫鑫，周智敏(國防科技大學 電子科學與工程學院，長沙 410073)

摘要：距離遷移(RM)算法能夠精確校正近場距離徙動，同時通過使用快速傅里葉變換可以達到很高的計算效率，具有應用于近場MIMO雷達三維實時成像的潛力。RM算法應用于近場MIMO成像的主要挑戰是設計合適的陣列結構。文中利用球面波分解為無窮多個平面波的方法推導了MIMO雷達近場三維RM成像算法,在深入分析算法實現流程的基礎上得到了RM算法對MIMO陣列構型的四條約束條件。提出了一種適用RM算法的MIMO陣列設計方法，并利用所提方法設計了MIMO陣列，結合仿真，分析了所設計陣列的成像性能。

關鍵詞：MIMO雷達；三維成像；距離遷移；陣列設計

0引言

近年來，多輸入多輸出(MIMO)雷達三維成像獲得了越來越多研究人員的關注[1-5]。MIMO雷達是指多個發射天線獨立發射信號以及多個接收天線獨立接收信號的雷達系統。MIMO雷達具有高數據獲取率的優勢，這極大地提高了雷達實時成像性能。此外，為了獲得高分辨率三維圖像，傳統的單站雷達需要大量的天線陣元，相反，二維MIMO陣列只需要使用較少的天線陣元，進而可以大大降低系統成本。得益于此，MIMO雷達廣泛應用在探地、穿墻和安檢等領域[1-7]。

MIMO雷達的N發M收的數據獲取方式增加了成像處理的復雜度，所以在探地、穿墻等應用中大多采用后向投影(BP)方法進行成像。BP方法運算量巨大，不適用于實時成像。距離徙動(RM)算法利用快速傅里葉變換(FFT)快速信號處理能力，可以大幅提高成像速度，MIMO雷達特殊的數據獲取形式使得RM算法很難直接應用于MIMO雷達成像。王懷軍等[8]研究了遠場下RM算法在MIMO雷達二維成像中的應用。在遠場假設下，可以通過多個頻譜支撐區的組合獲得完整的目標頻譜支撐區。文獻[1]采用駐定相位法將RM算法拓展到近場MIMO雷達三維成像，但是，并不是所有的MIMO陣列都能使用RM算法成像。實際上，RM算法對陣列構型有嚴格的約束條件，需要將RM算法與陣列設計相結合來考慮問題。

由等效陣列的理論可得，遠場窄帶條件下，MIMO陣列的方向圖等于發射陣列方向圖和接收陣列方向圖的乘積[9]。這使得可以分別調整發射陣列或者接收陣列的性能來得到完整的MIMO陣列的性能[10]。然而寬帶近場條件下滿足約束條件的陣列設計方法需要進一步研究。

1MIMO陣與等效陣

如圖 1所示，在三維笛卡爾坐標系下，假設二維MIMO陣列位于Z=0的平面上，使用aT(x,y)表示二維發射陣列，aR(x,y)表示二維接收陣列。遠場條件下，常用的等效陣列形式有雙程虛擬陣列和單程協同陣列[5,11]，其中雙程虛擬陣列廣泛應用于主動式雷達成像。本文后續分析中，等效陣列即指雙程虛擬陣列。遠場窄帶條件下，發射陣列和接收陣列的方向圖為

AT(u,v)=∫x∫yaT(x,y)e-jxue-jyvdxdy

(1)

AR(u,v)=∫x∫yaR(x,y)e-jxue-jyvdxdy

(2)

式中：u=ksinθcosφ、v=ksinθsinφ，θ代表入射方向的高度角，φ代表入射方向的方位角，k為波數。等效陣列aE(x,y)的方向圖AE(u,v)等于發射陣列和接收陣列方向圖的乘積[9]。即

AE(u,v)=AT(u,v)×AR(u,v)=

FT2D{aT(x,y)}×FT2D{aR(x,y)}=

FT2D{aT(x,y)?aR(x,y)}=

FT2D{aE(x,y)}

(3)

式中：“?”表示卷積；FT2D{·}代表二維傅里葉變換。式(3)表明，等效陣列可以表示為發射陣列和接收陣列的空間位置卷積，N個發射陣元和M個接收陣元可以獲得NM等效陣元。

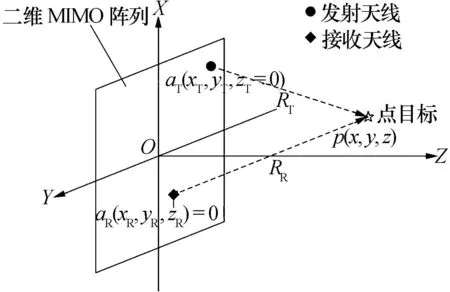
圖1　二維MIMO陣列成像場景

一般而言，等效陣列相同的MIMO陣列在近場和遠場條件下的性能并不相同。在近場高分辨率成像中，可以用上述表達式近似分析陣列性能[10]。

2RM成像算法對MIMO陣列構型的約束

2.1算法原理

圖 1為近場條件下二維MIMO陣列成像場景，其中發射天線坐標為(xT,yT,zT=0)，接收天線坐標為(xR,yR,zR=0)，目標散射特性函數為f(x,y,z)。假設發射的電磁波為步進頻率信號，波數為k。近場條件下，可以忽略電磁波傳輸時的衰減。則目標回波

s(xT,yT,zT=0,xR,yR,zR=0,k)=

∫∫∫f(x,y,z)e-jkRTe-jkRRdxdydz

(4)

其中

分別代表接收天線到目標點的距離和發射天線到目標點的距離。利用球面波可以分解為無窮多個平面波的原理[12]

e-jkRT=∫∫e-jkxT(x-xT)-jkyT(y-yT)-jkzTzdkxTdkyT

(5)

e-jkRR=∫∫e-jkxR(x-xR)-jkyR(y-yR)-jkzRzdkxRdkyR

(6)

S(kxT,kyT,kxR,kyR,k)=∫∫∫f(x,y,z)e-jkxx-jkyy-jkzzdxdydz

(7)

式(7)中

S(kxT,kyT,kxR,kyR,k)?FT4D{s(xT,yT,xR,yR,k)}

式中：(x,kx)為傅里葉變換對；kx為空間頻率；其他類似。

由式(7)可以得到

(8)

式(8)即為目標三維重構結果。

2.2RM算法對MIMO陣列的約束條件

成像處理中需要對空域坐標進行四維傅里葉變換，由奈奎斯特采樣定律可得，空間采樣頻率必須大于兩倍最大空間頻率。所以MIMO陣列必須滿足:

1) 發射陣列在高度向和方位向分別滿足奈奎斯特采樣定律；

2) 接收陣列在高度向和方位向分別滿足奈奎斯特采樣定律。

當不滿足上述條件時，采用RM算法不能得到正確的圖像，會出現分辨率下降、距離遷移校正出錯等問題。后文對此給出了仿真分析。

另外，成像需要進行五維數據到三維數據的映射，為了使得映射之后的空間譜采樣間隔一致，要求發射陣列和接收陣列的空間譜采樣間隔相等。即

(9)

式中：ΔKxT為空間頻率kxT的采樣間隔；其他類似。根據傅里葉變換空域和頻域的關系，為了滿足式(9)，要求

(10)

式中：NxT代表發射天線x維度FFT點數；ΔxT代表發射陣列x維度陣元間隔；其他類似。實際應用中，陣元數目可能小于所需FFT點數，此時只需要補零即可解決該問題。當陣元數目恰好等于所需FFT點數時，式(10)表示發射陣列和接收陣列的尺寸完全相等。由此可以得到MIMO陣列需要滿足的另外兩個條件：

3) 補零之后發射陣列和接收陣列在方位向的長度相等；

4) 補零之后發射陣列和接收陣列在高度向的長度相等。

除了上述的四條約束條件外，另外一個很顯然的約束就是要求接收陣列和發射陣列都是均勻采樣。

3陣列設計

3.1陣列設計方法

在雷達成像中，需要配置MIMO陣列以滿足系統性能要求。本小節結合2.2節提出的四條約束條件，在分析陣列性能的基礎上，提出適用RM算法的MIMO陣列設計方法。

由切片投影理論可得[13]，二維陣列在某個方向的成像性能由陣列在該方向的投影決定。以方位向分辨率為例，圖 2為成像場景在方位向-距離向平面內的投影、點目標與陣列孔徑。

圖2　方位向分辨率分析示意

邊緣的夾角分別為θ1、θ2，kc表示中心波數，LA表示等效陣列在方位向投影的長度。則該點目標成像方位向分辨率為

(11)

式中：αwin表示窗函數展寬因子。當等效陣列無冗余時，窗函數為矩形窗，此時αwin=0.886；當等效陣列存在冗余時，窗函數因子由具體的冗余窗決定。為簡單起見，通常以點目標位于陣列中垂線上距離為y0處的分辨率作為分辨率指標。此時θ1+θ2=π，tanθ1=2y0/LA，代入式(11)可得到

(12)

對于給定的分辨率，通過式(12)即可算出二維等效陣列方位向尺寸。同理，高度向尺寸可以通過類似方法獲得。

圖像中柵瓣的出現是由空間采樣間隔較大，導致空間譜缺失引起的。事實上，只需要確保所關心成像區域內不出現柵瓣即可。假設圖3中點目標P為成像區域的邊界點，則陣元間隔由下式確定

(13)

在確定了陣元間距之后，結合前文得到的陣列尺寸，即可得到方位向陣元數目。類似地，可以得到高度向的陣元數目。

確定二維等效陣列尺寸和陣元數目之后，為了使所設計MIMO陣列滿足四條約束條件，不可避免地要考慮冗余的情況。仍以二維等效陣列在方位向的投影為例，圖3中等效陣列在方位向投影得到的獨立位置個數為NEA，考慮冗余窗為梯形的情況，離散梯形窗的表達式為

Trape(n|m)=

(14)

Trape(n|m)即等效陣列aE(x,y)在方位向的歸一化投影aEA，記aEA=Trape(n|m)。由式(3)可得

aEA=Trape(n|m)=aTA?aRA

(15)

式中：aTA、aRA表示發射陣列和接收陣列在方位向的歸一化投影，考慮TA、aRA均為矩形窗的情況，由式(14)和式(15)去卷積可得

(16)

由式(16)可得，每一個m的取值對應兩種陣列配置，如圖 3所示。兩種陣列的結構實際上是一致的，只是發射陣列和接收陣列互換而已。

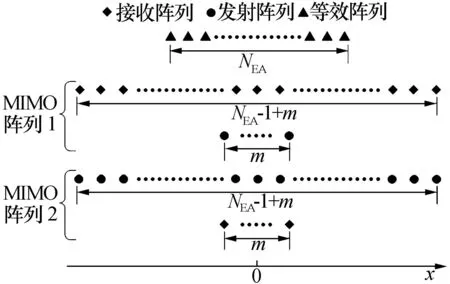
圖3　式(16)表示的兩種MIMO陣列配置

雷達目標散射截面(RCS)與視角有關，一般要求等效陣列和MIMO陣列的視角盡量保持一致[5]，所以圖3中發射陣列和接收陣列的中心是重合的。同樣地，可以用類似方法確定高度向陣列分布。

由式(16)可以確定出NEA種MIMO陣列配置，在遠場假設下，這NEA種陣列具有相同的等效陣列以及一致的性能。獲得具體MIMO陣列之后可以得出近場條件下方位向分辨率表達式

(17)

其中

(18)

式中：LTA、LTR為發射陣列和接收陣列在方位向投影的尺寸，LTA+LRA=2LA；窗函數因子αwin=g(LTA,LRA)，g(·)為超越函數算子。可以看出，近場條件下，NEA個MIMO陣列的性能是不同的。在二維等效陣列方位向投影尺寸LA一定的情況下，最優化問題描述如下

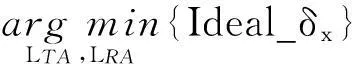
(19)

式(17)中分子和分母之間存在耦合，所以直接求解式(19)較為復雜。為了簡化分析，我們獨立分析式(19)的分子和分母。最優化問題等價為

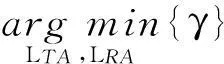
(20)

(21)

綜上所述，近場二維MIMO陣列的設計步驟為：

1) 根據分辨率指標確定二維等效陣列孔徑尺寸；

2) 根據柵瓣水平或成像區域確定陣元個數；

3) 結合RM算法對MIMO陣列的四條約束條件，由等效陣列確定具體MIMO陣列形式；

4) 近場條件下，從步驟3得到的MIMO陣列中選擇分辨率性能最優的陣列。

步驟4)中的優化目標不只局限于分辨率，例如，可以選擇陣元數目最少的MIMO陣列，或者可以在陣元數目和分辨率之間取一個折中。

3.2設計實例

陣列要求：設計二維MIMO陣列，要求在距離25 cm處方位向和高度向分辨率0.35 cm，陣列正前方成像區域內不出現柵瓣，同時滿足RM算法要求的四條約束條件。

假設信號體制為步進頻，信號帶寬3 GHz，中心頻率28.5 GHz，頻率步進間隔為30 MHz。按照前文所述設計步驟：

1) 確定陣列尺寸；將分辨率要求代入式(12)可得，等效陣列尺寸為50 cm×50 cm。

2) 確定等效陣列陣元數目；將kc=28.5 GHz、θ1=π/4、θ2=3π/4代入式(13)中，得到等效陣元間隔為0.331 cm，結合步驟1)得到的等效陣列尺寸，陣元數目N2≥1512。

3) 結合RM算法確定MIMO陣列構型；根據不同的發射陣列和接收陣列長度(個數)的組合，共有151種陣列結構。

4) 結合近場條件，確定優化目標，從步驟3)中選擇最優MIMO陣列構型；設定分辨率最佳為優化目標，圖4為等效陣列長度一定(50 cm)的情況下方位向分辨率隨發射(接收)陣列長度變化的曲線。選擇分辨率性能最優為優化目標，所設計的MIMO陣列如圖 5a)所示，其中發射陣元數目35×116,接收陣列數目116×35；如果犧牲一定的分辨率指標，選擇陣元數目最少為優化目標，所設計陣列為“十”字陣列，如圖 5b)所示，其中發射陣元數目為151，接收陣元數目為151。

圖4　等效陣列長度一定時，方位向分辨率與發射陣列長度

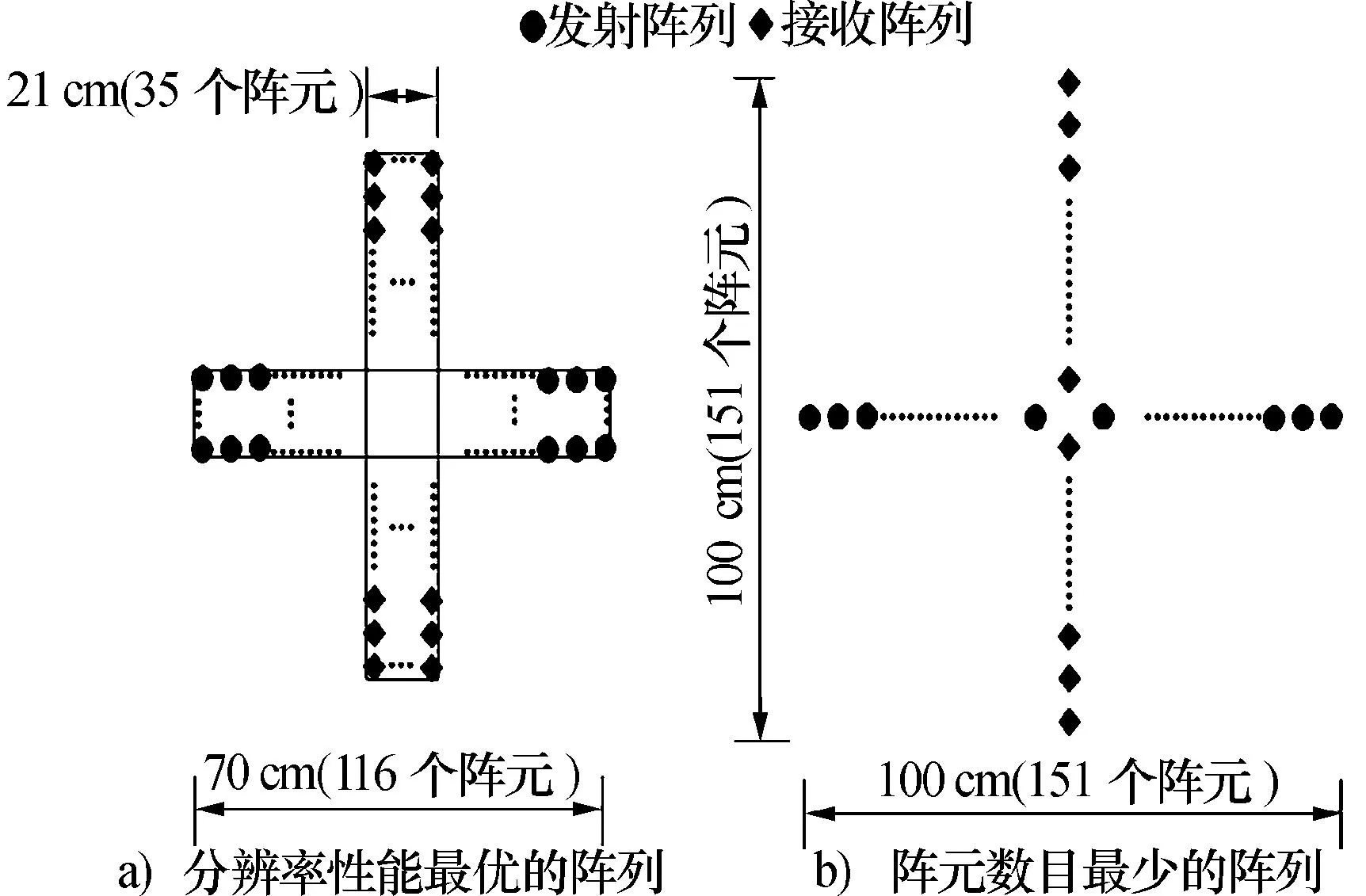
圖5　MIMO陣列設計結果

4仿真分析

為了驗證RM算法的適用性以及所設計陣列的成像性能，采用Matlab仿真平臺進行了成像仿真。陣列a指圖5a)中所示陣列，陣列b指圖5b)中所示陣列，二者具有相同的等效陣列尺寸。用RM算法對25 cm處點目標成像，其他參數與3.2節所述相同。

陣列a、b成像結果如圖6、圖7所示，可以看出，基于約束條件設計的陣列使用RM算法能夠得到高質量的成像結果。表1列出了兩種陣列成像結果的分辨率及峰值旁瓣比性能，基于最優分辨率設計的陣列a較陣列b具有更好的分辨率性能和峰值旁瓣比性能，峰值旁瓣比的提高得益于等效陣列冗余引入的窗函數。

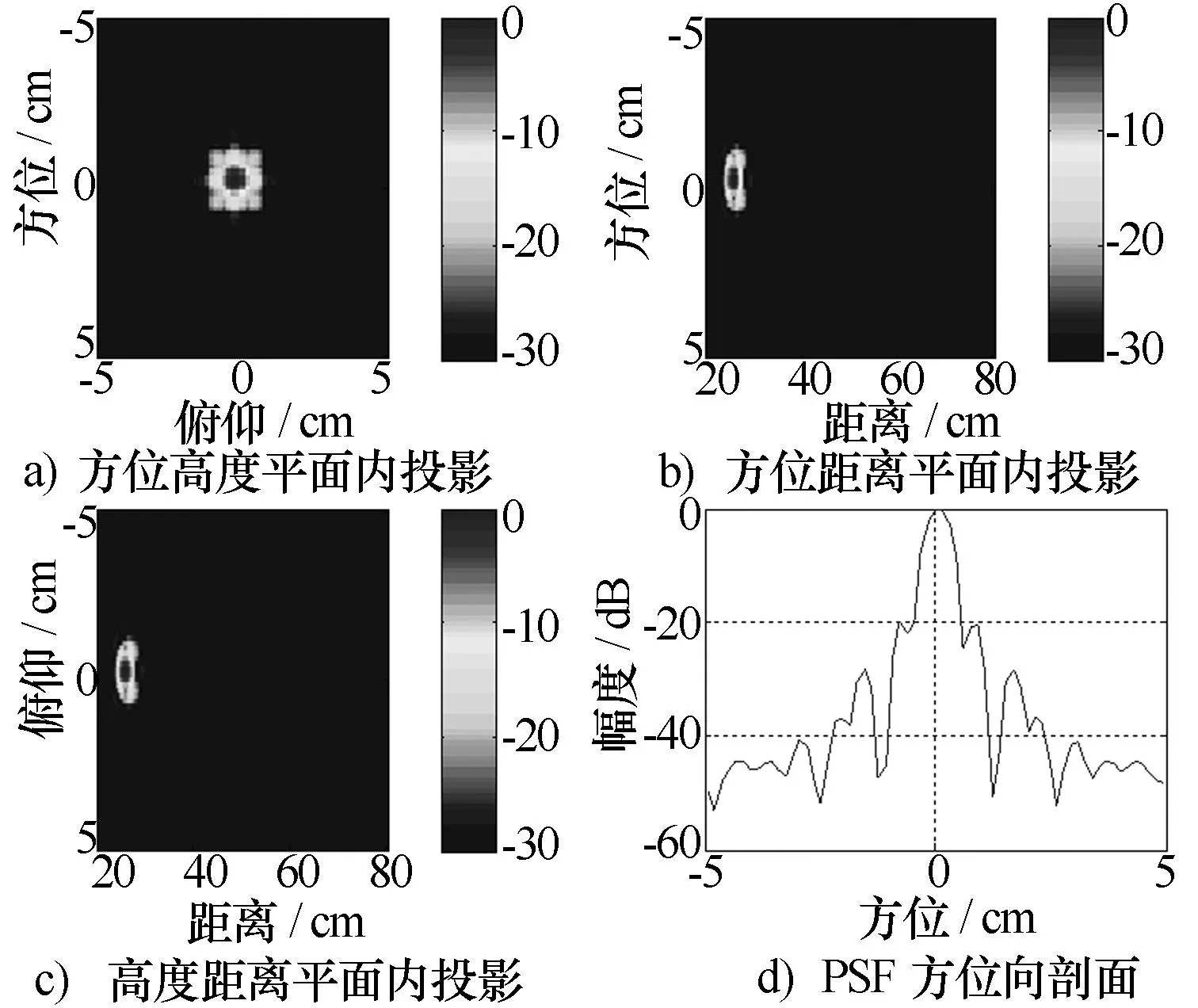
圖6　陣列a的RM成像結果

圖7　陣列b的RM成像結果

理想IRW/cmIRW/cmPSLR/dB陣列a0.470.58-9.8陣列b0.390.48-20.1

保持等效陣列尺寸仍為50 cm×50 cm，構造圖8a)所示MIMO陣列，記為陣列c。該陣列的發射天線方位向不滿足采樣定律，接收天線高度向不滿足采樣定律。使用BP算法和RM算法分別對其成像，得到的結果如圖8b)、圖8c)所示。圖8d)給出了PSF的方位向剖面，陣列c的方位向理論分辨率為0.33 cm。BP成像的方位向分辨率為0.326 8 cm，與理論值相吻合。RM成像的方位向分辨率為0.741 8 cm，分辨率性能惡化為理論分辨率的兩倍。此外，RM成像結果的距離向位置發生偏移，由25 cm偏移到35.4 cm，這是因為不滿足采樣定律導致色散關系不成立，自然無法正確校正距離徙動。上述結果證明不滿足約束條件的陣列c并不適合使用RM方法成像，進一步說明為了使用RM算法，必須設計符合約束條件的MIMO陣列。

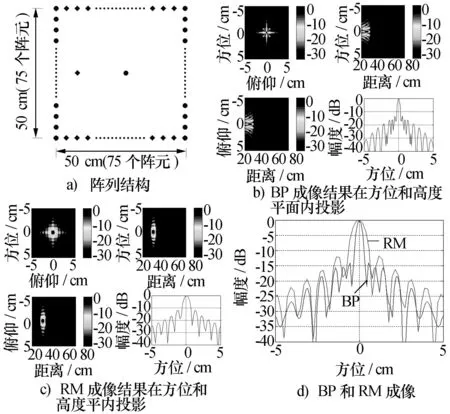
圖8　陣列c分別采用BP和RM算法的成像結果

此外，使用陣列b進行了BP成像的仿真，采用32 GB內存、8核2.2 GHz處理器的服務器平臺，得到的BP成像耗時和RM成像耗時如表2所示。可以看出RM算法的運算效率大幅提高，證明了RM算法具有很好的實時性能。

表2陣列b使用BP和RM成像耗時對比s

成像算法成像耗時BP46026BM86

5結束語

RM算法的運算效率遠高于BP算法，具有應用于實時成像系統的潛力。但是RM算法對MIMO陣列構

型的要求更為苛刻。本文提出了適合使用RM算法成像的MIMO陣列的設計方法，基于不同的優化目標，能夠得到不同的陣列構型。實際中，可以采用折中的方法兼顧陣元數目和陣列性能。仿真分析證明了設計方法的正確性和有效性，另外，也證明了RM算法可以獲得很高的成像性能和實時性能。

參 考 文 獻

[1]ZHUGE X D, YAROVOY A G. Three-dimensional near-field MIMO array imaging using range migration techniques[J]. IEEE Transactions on Image Processing, 2012, 21(6): 3026-3033.

[2]DAVID S, DOUGLAS M M, THOMAS H. Near-field three-dimensional radar imaging techniques and applications[J]. Applied Optics, 2010, 49(19): 83-93.

[3]SHEEN D M, McMAKIN D L, HALL T E. Three-dimensional millimeter-wave imaging for concealed weapon detection[J]. IEEE Transactions on Microwave Theory and Techniques, 2001, 49(9): 1581-1592.

[4]ZHUGE X D. Short-range ultra-wideband imaging with multiple-input multiple-output arrays[D]. Delft: Delft University of Technology, 2010.

[5]LU B Y, ZHAO Y, SUN X, et al. Design and analysis of ultra wide band split transmit virtual aperture array for through the wall imaging[J]. International Journal of Antennas and Propagation, 2013, 139(3): 170-174.

[6]劉鵬飛, 陸必應, 孫鑫, 等. 基于子陣劃分的二維穿墻MIMO陣列設計[J]. 雷達科學與技術, 2014, 12(5): 539-545.

LIU Pengfei, LU Biying, SUN Xin, et al. A method of two-dimensional MIMO planar array design based on sub-array segmentation for through-wall imaging[J]. Radar Science and Technology, 2014, 12(10): 539-545.

[7]ZHUGE X D, YAROVOY A G, SAVELYEV T, et al. Modified kirchhoff migration for UWB MIMO array-based radar imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(6): 2692-2703.

[8]王懷軍. MIMO雷達成像算法研究[D]. 長沙: 國防科學技術大學，2010.

WANG Huaijun. MIMO radar imaging algorithms[D]. Changsha: National University of Defense Technology, 2010.

[9]AHMED S S, SCHIESSL A, GUMBMANN F, et al. Advanced microwave imaging[J]. IEEE Microwave Magazine, 2012,13(6): 26-43.

[10]ZHUGE X D, YAROVOY A. Near-field ultra-wideband imaging with two-dimensional sparse MIMO array[C]// European Conference on Antennas & Propagation.[S.l.]: IEEE Press, 2010: 1-4.

[11]AHMAD F, KASSAM S A. Coarray analysis of the wide-band point spread function for active array imaging[J]. Signal Processing, 2001, 81(1): 99-115.

[12]MORSE P, FESHBACH H. Methods of theoretical physics[M]. New York: McGraw Hill Companies, 1968.

[13]SCHWARTZ J. Ultra sparse, ultra wideband arrays[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1998, 45(2): 376-393.

王武男，1992年生，碩士研究生。研究方向為新體制雷達系統與技術。

陸必應男，1976年生，副教授。研究方向為新體制雷達系統與技術。

孫鑫男，1986年生，博士研究生。研究方向為新體制雷達系統與技術。

周智敏男，1957年生，教授。研究方向為新體制雷達系統與技術。

3-D Imaging and 2-D MIMO Arrays DesignBased on Range Migration Algorithm

WANG Wu，LU Biying，SUN Xin，ZHOU Zhimin

(College of Electronic Science and Engineering,National University of Defense Technology,Changsha 410073, China)

Abstract：Because of compensating completely the curvature of wave-front in near field and high computational efficiency by using fast Frourier transform, range migration algorithm (RMA) has the potential for MIMO radar 3-D real-time imaging. The main challenge of using RMA in near field MIMO imaging is to design appropriate MIMO array topology. In this paper, the formulation of MIMO 3-D imaging using RMA is derived by using the theory that a spherical wave can be decomposed into infinite superposition of plane waves. Analyzing the RMA implementation processes, we obtain four constraints about MIMO topology. The designing method of MIMO arrays for RMA is proposed in this paper, and MIMO arrays are designed. Performance of these arrays and accurate imaging reconstruction of RMA are analyzed with numerical simulations.

Key words：MIMO radar; 3-D imaging; range migration; array design

中圖分類號：TN957.51

文獻標志碼：A

文章編號：1004-7859(2016)02-0038-05

收稿日期：2015-10-27

修訂日期：2015-12-25

通信作者：王武Email：wangwu163@.com

DOI：·信號處理· 10.16592/ j.cnki.1004-7859.2016.02.009