基于掃頻法的簡支梁模態參數測定

歸文強，袁小慧，夏芝安

（長安大學汽車學院，陜西 西安 710064）

?

基于掃頻法的簡支梁模態參數測定

歸文強，袁小慧，夏芝安

（長安大學汽車學院，陜西 西安 710064）

摘 要：在機械工程中振動是很普遍的現象，分析系統的固有頻率和固有振型可以避免系統在使用過程中出現共振現象，減少振動對系統的影響。用掃頻法得到簡支梁系統的固有頻率和固有振型，與理論值進行對比誤差不大于3.8%。測定簡支梁的模態參數為研究復雜系統提供理論基礎和參考方法。

關鍵詞：簡支梁；固有頻率；振型；共振

10.16638/j.cnki.1671-7988.2016.02.037

CLC NO.: U463.5 Document Code: A Article ID: 1671-7988(2016)02-100-03

引言

簡支梁是工程中常見振動模型，研究并掌握其工程分析方法具有重要的實踐意義[1]。本文通過對等截面簡支梁系統的研究，對其運用試驗測試的方法，找出該系統振動的固有頻率和前三階振型，揭示該系統在外激勵下產生共振現象的可能性和范圍，以避免對機構破壞最大的共振的發生，達到主動避振的目的，為復雜機構的振動分析提供一定的參考[2]。

1、實驗模態分析法

1.1 簡支梁相關參數說明

本文中研究的簡支梁的幾何參數為長:L=1.00m，寬:B= 0.05m，高:H=0.012m，簡支梁密度，材料彈性模。

圖1 簡支梁結構簡圖

1.2 實驗原理

理論上，簡支梁應該有無限個固有頻率和主振型。如果給梁施加了一個合適大小的激擾力，且該力的頻率正好等于梁的某階固有頻率，就會產生共振，對應于這一階固有頻率的確定的振動形態叫做這一階的主振型，這時其他各階振型的影響小得可以忽略不計。首先通過掃頻法找到梁各階的固有頻率，然后讓激振力頻率等于各階固有頻率，使梁產生共振，最后測定共振狀態下梁上各測點的振動加速度值[3-4]。

由于對簡支梁采用的是正弦信號激勵，故可知輸出為：

其中，Y是簡支梁上測點的位移；Y’為速度;Y’為加速度。為振動的固有頻率；A為振幅。

1.3 實驗方法

利用掃頻法從信號發生器內，發出1-300HZ的正弦信號，此信號通過數據線一方面傳遞給Synergy，另一方面傳遞給功率放大器，再傳給激振器，激振器以此頻率激振簡支梁。當激振器的頻率與簡支梁的固有頻率一致時，簡支梁便產生共振，此時，梁的振動通過加速度傳感器，傳遞到Synergy。通過FFT變換后就可以看到其前三階的固有頻率。得到前三階固有頻率后，讓信號發生器依次產生前三階固有頻率處的正弦信號。同時，依據理論知識，在簡支梁上依次按1,2,3階固有頻率振動時的主振型布置測量點。測量在各階固有頻率下，所布置的各個點的加速度最大值，并記錄。同時，進行FFT變換查看其相頻特性，記錄各點相位差。

2、結果分析

2.1 前三階固有頻率

利用Synergy數據采集儀軟件分析功能將接收到加速度傳感器的信號進行FFT變化得到其頻域信號，可以從中讀出簡支梁前三階固有頻率，如圖3所示。簡支梁前三階固有頻率分別為: 27.1Hz、109.9Hz、244.3Hz。實驗過程中由于儀器使用交流電，產生干擾信號，圖中標出的50Hz頻率為交流電信號頻率。

圖2 簡支梁前三階固有頻率

2.2 簡支梁前三階振型

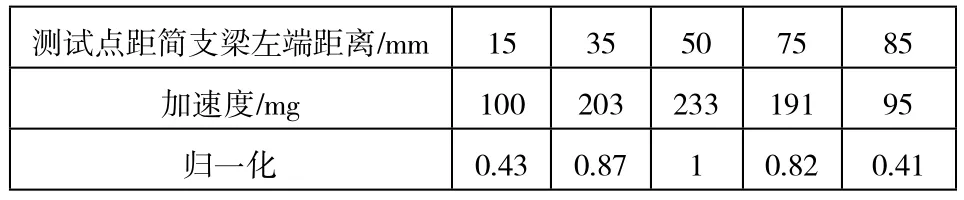
表1 第一階固有振型相應位置加速度

由實驗得到前三階固有頻率，然后將信號發生器分別設置為前三階固有頻率產生正弦信號對簡支梁進行激勵，用加速度傳感器測量簡支梁相應位置處的加速度值。根據各測點相位關系確定該點的振幅方向，然后歸一化處理加速度值，即可繪出各階振型[5-6]。前三階固有振型相應位置的加速度測量值見表1至表3，以簡支梁最左端作為測試零點。

表2 第二階固有振型相應位置加速度

表3 第三階固有振型相應位置加速度

根據理論計算數據和實驗測量，得出簡支梁前三階固有頻率見表4，可以看出，兩種方法得出的固有頻率基本一致，實驗測量值與理論值誤差保持在3.8%以內，實驗方法是可行的。

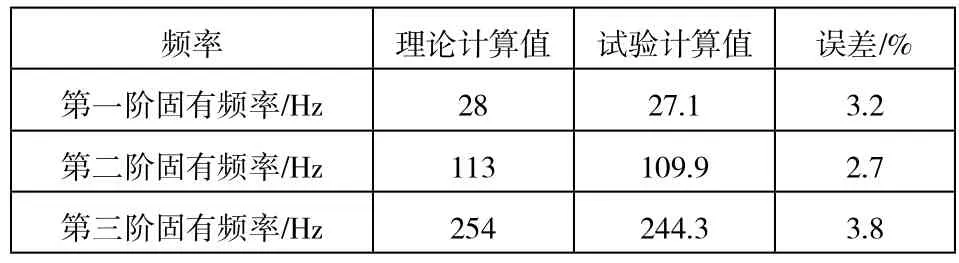
表4 簡支梁前三階固有頻率理論值與試驗測量值比較

根據Matlab計算值和實驗模態法得出的數據，分別繪制簡支梁前三階振型，如圖3-5所示。圖中看出，兩種方法得出的振型基本一致，由于實驗模態法測量點有限，繪圖得出的振型比較粗糙。

圖3 一階主振型

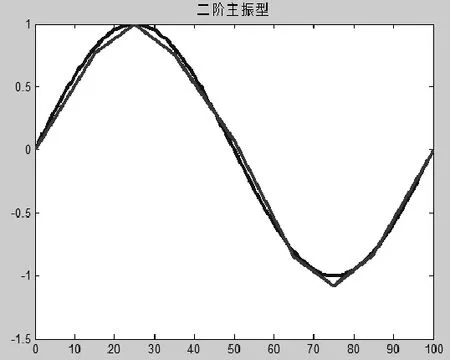
圖4 二階主振型

圖5 三階主振型

3、結論

通過試驗手段對簡支梁進行研究，得出了振動系統前三階的固有頻率和固有振型。實驗模態分析法中難免會有人為因素和儀器精度的影響，所以與理論值存在一定誤差。結果表明，通過試驗方法對等截面簡支梁固有頻率和固有振型求解，為分析工程實際中振動現象、避免共振提供了一套科學的參考方法。實驗過程中發現，高性能儀器的使用有利于實驗問題方便高效的求解。

參考文獻

[1] 諸德超,邢譽峰. 工程振動基礎[M].北京:北京航空航天出版社,2004.

[2] 戴麗玲.簡支梁固有頻率與固有振型的實驗室測量與理論分析[J].昆明學院學報,2008,30(4): 86-89.

[3] 李偉民,何偉,楊琳.簡支梁振動特性的理論分析及實驗研究[J].貴州教育學院學報:自然科學版,2007(4):44-49.

[4] 劉習軍,賈啟芬.工程振動理論與測試技術[M].北京:高等教育出版社,2004.

[5] 文濤,胡青春. 基于MATLAB語言的多自由度振動系統的固有頻率及主振型計算分析[J].中國制造業信息化,2007(1): 78-81.

[6] 梁虹,梁潔,陳躍斌.信號與系統分析及MATLAB實現[M].北京:電子工業出版社,2002.

The Test of the Modal Parameter of the Free Beam Based on Frequency Sweep Method

Gui Wenqiang, Yuan Xiaohui, Xia Zhi’an
( School of Automobile Chang'an University, Shaanxi Xi'an 710064 )

Abstract:The vibration is a common phenomenon in mechanical engineering. Analyzing the natural frequencies and natural vibration types of the system can avoid the resonancephenomenon in the course of using and reduce the influence to the system. The natural frequencies and natural vibration types of the free beam that was got by frequency sweep method are similar to the theoretical data, and the error is not biggger than 3.8%. The test of the modal parameter of the free beam can provide methods and theoretical basis to the study of the complex systems.

Keywords:free beam; natural frequency; natural vibration type; resonance

作者簡介：歸文強，就讀于長安大學。

中圖分類號：U463.5

文獻標識碼：A

文章編號：1671-7988(2016)02-100-03