把握二次根式中的數學思想
2016-04-12 07:50:20吳育弟
初中生天地 2016年8期
□吳育弟
?
把握二次根式中的數學思想
□吳育弟
一、估值思想
例1 a、b是兩個連續整數,若a<<b,則a、b分別是().
A. 2,3
B. 3,2
C. 3,4
D. 6,8
分析:7介于4與9之間,即4<7<9,則利用不等式的性質可以求得介于2與3之間.
解:∵4<7<9,
故選A.
二、數形結合思想

分析:根據二次根式的性質,可化簡二次根式,根據整式的加法,可得答案.
解:由圖知,a<1,
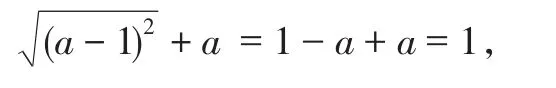
點評:數形結合的關鍵在于能否將代數問題蘊含的幾何圖形、幾何知識抽取、轉化出來,再進行解決.
三、方程思想
,則(x+y)2014等于().
A. -1 B. 1
C. 32014D. -32014
分析:根據非負數的性質列出方程求出x、y的值,代入所求代數式計算即可.
解:∵
∴{x - 1 = 0,解得{x = 1, y + 2 = 0,y = -2.
∴(x+y)2014=(1-2)2014=1.
故選B.
四、分類討論思想
分析:由題意可知,可分x≥-3 或x<-3兩種情況討論.
解:當x≥-3時,

五、整體思想
分析:根據x、y的值,先求出x-y和xy,再化簡原式,代入求值即可.
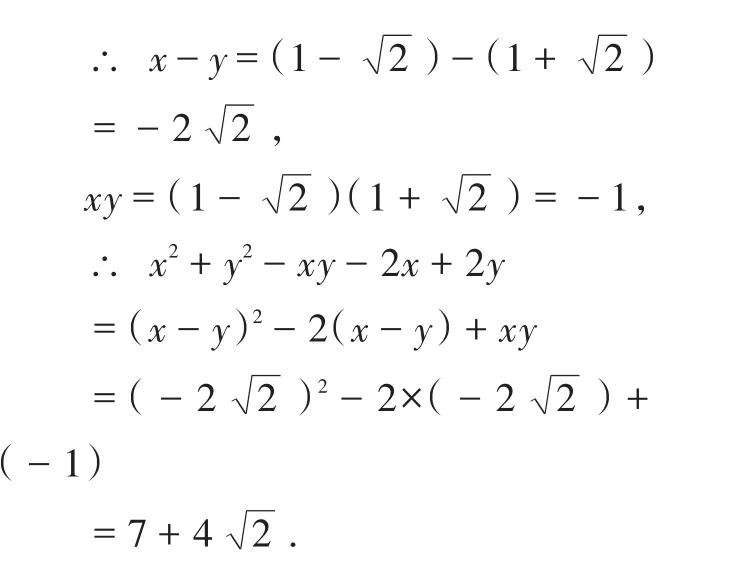
點評:整體思想就是化零為整、化分散為集中的一種數學思想.本題中就是把x-y和xy看做一個整體,在求解的過程中運用了整體代入的數學思想,既簡潔又巧妙.
六、轉化思想
解:原式

點評:轉化思想是將不易解決的問題,設法變成我們容易解決的問題,從而達到將抽象轉化為具體、復雜轉化為簡單的目的的一種數學思想.在本題中,是將陌生的形式轉化成熟悉的積的乘方公式,再利用平方差公式求解.
猜你喜歡
華人時刊(2022年7期)2022-06-05 07:33:26
當代陜西(2021年13期)2021-08-06 09:24:34
民用飛機設計與研究(2020年4期)2021-01-21 09:15:02
人大建設(2019年4期)2019-07-13 05:43:08
當代陜西(2019年12期)2019-07-12 09:11:50
電子制作(2018年18期)2018-11-14 01:48:24
山東工業技術(2016年15期)2016-12-01 05:31:22
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
漫畫月刊·炫版(2014年3期)2014-05-27 04:17:21

