連續旋轉的光纖陀螺全溫標度因數快速建模補償方法

張曉雅，楊志懷，宋麗薇，馬 林

（天津航海儀器研究所，天津 300131）

連續旋轉的光纖陀螺全溫標度因數快速建模補償方法

張曉雅，楊志懷，宋麗薇，馬 林

（天津航海儀器研究所，天津 300131）

在全溫范圍內應用的光纖陀螺，標度因數誤差是其主要的誤差之一。特別是在大角速率或者高精度應用時，光纖陀螺的標度因數誤差甚至超過零偏漂移誤差。在實際使用中，需對陀螺標度因數在全溫范圍內進行建模和補償。對光纖陀螺標度因數誤差機理進行詳細分析后，提出了一種連續旋轉的光纖陀螺全溫標度因數快速建模補償方法。基于單軸速率轉臺的連續旋轉，可以自動快速完成標度因數全溫建模且工程實現簡單易行。更重要的是該方法可以有效識別標度因數在全溫范圍內的變化拐點，提高建模和補償的精度。對比試驗結果表明，采用此方法后能精確測得某型光纖陀螺全溫工作的標度因數真實拐點為48℃，全溫標度因數補償精度優于15×10-6，較按照GJB2426-2004進行的多點測試后補償提高10%左右。

光纖陀螺；標度因數；溫度建模；補償

當溫度變化時光源、Y波導集成光學調制器等光學元器件的平均波長會隨之變化，導致光纖陀螺的標度因數變化[1-2]。在全溫范圍內應用的光纖陀螺，特別是在大角速率或者高精度應用時，光纖陀螺的標度因數誤差會超過偏置漂移誤差，嚴重制約光纖陀螺的環境適用性。從機理上消除溫度帶來的標度因數誤差難度大、成本高，而基于理論機理的溫度誤差建模和補償是一種簡單有效的解決方法。特別是在全溫范圍內（-40℃～+60℃）對光纖陀螺的標度因數誤差進行建模和補償，對于提高標度因數穩定性指標有重要意義。

常用的建模方法有線性回歸模型[3-4]、多種神經網絡模型[5]等。前者結構簡單，工程實現容易，缺點是非線性補償能力弱；后者結構復雜，參數多，將物理過程看作一個黑箱模型，非線性函數逼近效果能力強，但工程實現困難。

常用的光纖陀螺標度因數測試方法是按照GJB2426-2004進行一系列的角速率測試，根據最小二乘法計算得到[6]。全溫條件下的光纖陀螺標度因數建模通常是選擇幾個典型的溫度點，分別進行標度因數測試，得到各溫度點對應的標度因數值作為標度因數補償模型的輸入[3-4]。上述這種光纖陀螺標度因數測試和建模方法由于頻繁操作速率轉臺效率低，且隨著建模精度需求增加更多的測試溫度點時，會大大增加測試時間和成本。本文提出了一種基于連續旋轉的光纖陀螺全溫標度因數快速建模補償方法。基于帶溫箱的單軸速率轉臺，在全溫條件下使其單向勻速旋轉即可自動快速完成標度因數在全溫條件下的建模，工程實現簡單易行。更重要的是該方法可以有效識別標度因數在全溫范圍內的變化拐點，無盲點地全面反映標度因數隨溫度變化的情況，從而提高建模和補償的精度。

1 光纖陀螺標度因數誤差機理

目前中高精度光纖陀螺均采用全數字閉環光纖陀螺方案，其中光纖陀螺敏感到的輸出信號與輸入角速率的關系可以表示為[3]

式中：ΩI為輸入角速度，Ω0為輸出角速度，L為光纖長度，D為光纖環直徑，λ為真空中的光波波長，C為真空中的光速，Kfp為Y波導的調制系數，Vpp為階梯波峰值電壓，N為D/A轉換器位數，KSF為光纖陀螺的標度因數。由式(1)可以看出，光纖陀螺的標度因數受到光纖敏感環圈長度和直徑、光波波長、Y波導半波電壓以及電路階梯波峰值電壓的影響，而這些因素又均受到溫度的影響。

全數字閉環光纖陀螺方案的優點是通過增加第二反饋回路可以精確跟蹤 Y波導半波電壓隨溫度的變化，即始終保持調制系數與Y波導半波電壓的乘積系數為 2π，從而提高標度因數的穩定性[7-8]。因此在理想閉環反饋狀態下，標度因數誤差僅由L、D的乘積和光波長λ決定。

光纖陀螺的標度因數溫度誤差可以表示為[9]

中高精度光纖陀螺通常采用超熒光摻鉺光纖光源(ASE)，其平均波長漂移有三種與溫度相關的來源，可以表示為[10]式中：第一項是有摻鉺光纖的固有溫度系數導致的固有的平均波長的變化，第二項和第三項分別表示泵浦波長和泵浦功率隨溫度變化導致的光源平均波長變化。通過優化設計，可以將ASE光源的溫度系數做到小于5×10-7/℃。

通過以上對標度因數誤差來源的分析并結合大量光纖陀螺實驗測試表明，其標度因數隨溫度變化具有較強的重復性和規律性，且通過溫度的一階最小二乘法進行建模和補償即可實現比較好的全溫標度因數性能。

2 標度因數溫度誤差建模和補償

標度因數的溫度誤差模型可以表示為

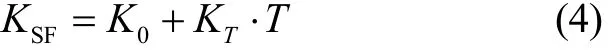
式中：K0是與溫度無關的標度因數，KT是與溫度相關的陀螺標度因數誤差系數，T為陀螺溫度。根據式(4)模型，光纖陀螺全溫標度因數通常的建模方法是選擇幾個典型的溫度點，分別按照GJB2426-2004進行標度因數測試，得到的結果作為標度因數補償模型的輸入，進而通過分段建模的方式進行補償[3-4]。

光纖陀螺的輸出可以表示為

式中：0Ω為光纖陀螺的固有零偏，ω為陀螺輸入轉速。將光纖陀螺的敏感軸朝天且固定于一勻速單向旋轉的單軸速率轉臺，此時由零偏引起的輸出標度因數測試誤差可以表示為

圖1 不同轉速下陀螺零偏對標度因數誤差影響Fig.1 Gyro bias’s influence on scale factor error at different rotating speeds

根據式(6)，圖1給出了不同轉速下，陀螺固有零偏對標度因數測試的影響曲線。通常中高級精度光纖陀螺的固有零偏在0.1 (°)/h以下，因此當轉臺速率大于50 (°)/s時，其對標度因數的誤差影響小于0.6×10-6。

當光纖陀螺在以較高速率勻速轉動時，陀螺輸出的變化即代表了溫度引起的標度因數變化。設置溫箱溫度激勵，讓光纖陀螺遍歷全溫范圍即可完成光纖陀螺的全溫標度因數連續建模。這種方法可以有效識別標度因數在全溫范圍內的變化拐點，無盲點地全面反映標度因數隨溫度變化情況，提高建模精度。選定溫度拐點后，采用最小二乘法可以實現光纖陀螺分段式標度因數建模。

3 試驗驗證

圖2(a)給出了一只光纖陀螺采用連續旋轉速率法時的溫度激勵曲線，圖2(b)給出了在此溫度激勵下的光纖陀螺輸出曲線，其代表了不同溫度點下的光纖陀螺標度因數變化。圖3給出了同一只光纖陀螺采用常規國軍標方法進行的20℃一個采樣點的全溫標度因數建模。

從圖2～3中可以看出，連續旋轉法能全面反映各個溫度下光纖陀螺標度情況，有利于標度因數分段補償時選擇合適的拐點。傳統國軍標方法在測試點較少情況下不能完全精確反映光纖陀螺的標度因數在全溫條件下的變化情況。按照圖3所示的模型建模，當補償后的光纖陀螺工作在真實拐點48℃時，將發生較大的標度因數誤差。為避免上述問題，可以在建模時增加更多的采樣點，與此同時又會大大增加測試時間和成本，且不能精確反映全溫條件下光纖陀螺標度因數曲線的精確拐點位置。

通過上述方法對3只光纖陀螺分別進行了全溫標度因數建模，并采用單片FPGA實現光纖陀螺分段式全溫標度因數補償。最后，采用國軍標測試方法對其分別進行了多點測試驗證。表1為3支陀螺分別用兩種方法建模后的補償效果。

由于連續旋轉法建模方法更能捕捉精確的各段標度因數拐點，上述實驗中3只陀螺補償后的全溫標度因數重復性相比多點測試法建模，補償精度更高，標度因數重復性指標更優。

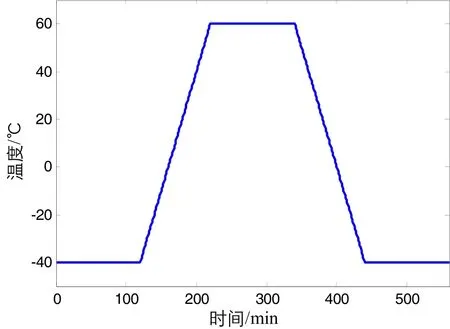
圖2 (a) 溫度激勵曲線Fig.2(a) Temperature curve

圖2 (b) 連續旋轉法標度建模Fig.2(b) Scale factor modeling by continuous rotation method

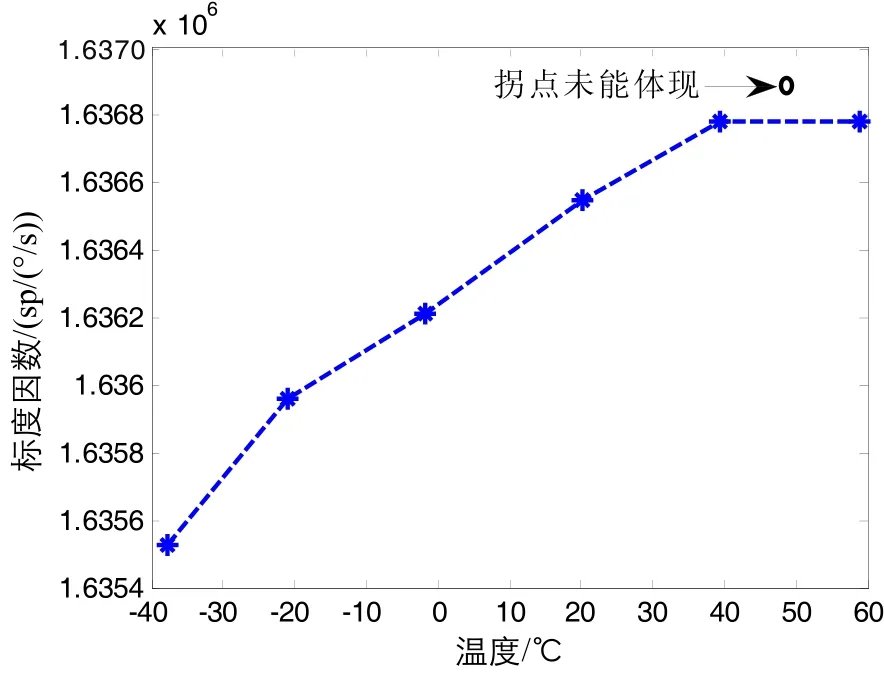
圖3 常規多點測試法標度因數建模Fig.3 Scale factor modeling by conventional mutipoint method

表1 兩種方法建模后全溫標度因數重復性對比Tab.1 Compensation results of two modeling methods

4 結 論

光纖陀螺標度因數溫度誤差主要受到L、D的乘積和光源波長λ隨溫度變化的影響。陀螺以較大速率勻速轉動時，陀螺的輸出變化直接反應標度因數隨溫度的變化關系。基于單軸速率轉臺，采用連續旋轉法對光纖陀螺進行全溫標度因數，可以在大大提高建模效率的同時實現全溫范圍內的標度因數變化無盲點測試，從而在分段擬合時可以精確選擇拐點位置，使得建模和補償精度更高。

（References）：

[1] Dagenais D M, Goldberg L, Moeller R P, et al. Wavelength stability characteristics of a high power amplified superfluorescent source[J]. Journal of Lightwave Technology, 1999, 17(8): 1415-1422.

[2] Zhao Dun-hui, Chen Jia-bin, Han Yong-qiang, et al. Temperature compensation of FOG scale factor based on CPSO-BPNN[C]//Control and Decision Conference. 2010: 2898-2901.

[3] Zhang Xiao-feng, Fan Hua-chun, Liang Yu. FOG output drift compensation based-on temperature gradients[J]. Piezoelectrics & Acoustooptics, 2010, 33(1): 38-40.

[4] 汪剛, 吉世濤, 藍燕, 等. 光纖陀螺標度因數溫度補償的工程應用[J]. 導航與控制, 2012, 11(1): 41-45. Wang Gang, Ji Shi-tao, Lan Yan, et al. FOG scale factor temperature compensation of engineering application[J]. Navigation and Control, 2012, 11(1): 41-45.

[5] 那永林, 李立坤, 吳衍記, 等. 光纖陀螺標度因數的測試誤差分析[J]. 中國慣性技術學報, 2012, 20(4): 473-477. Na Yong-lin, Li li-kun, Wu Yan-ji, et al. Measurement error analysis of FOG’s scale factor[J]. Journal of Chinese Inertial Technology, 2012, 20(4): 473-477.

[6] GJB2426A-2004. 光纖陀螺儀測試方法[S]. 國防科學技術工業委員會, 2004. GJB2426A-2004. Test methods for fiber optic gyroscope [S]. Commission of Science Technology and Industry for National Defense, 2004.

[7] 楊曄, 陳馨, 張桂才. 基于角速率積分法的光纖陀螺標度因數不對稱的測量方法[J]. 中國慣性技術學報, 2012 20(3): 343-347. Yang Ye, Chen Xin, Zhang Gui-cai. Measurement of fiberoptic gyroscope scale factor asymmetry based on angular rate integral technology[J]. Journal of Chinese Inertial Technology, 2012, 20(3): 343-347.

[8] Ko J, Fox D. Learning GP-Bayes filters via Gaussian process latent variable models[J]. Autonomous Robots, 2011, 30: 3-23.

[9] Nguyen-Tuong D, Peters J. Incremental online sparsification for model learning in realtime robot control[J]. Neurocomputing, 2011, 74(11): 1859-1867.

[10] 劉元元, 楊功流, 尹洪亮. 基于雙模型的光纖陀螺溫度補償方法[J]. 中國慣性技術學報, 2015, 23(1): 131-136. Liu Yuan-yuan, Yang Gong-liu, Yin Hong-Liang. Temperature compensation for fiber optic gyroscope based on dual models[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 131-136.

[11] Wang Xi-jiang, He Zu-yuan, Hotate K, et al. Reduction of polarization-fluctuation induced drift in resonator fiber optic gyro by a resonator with twin 90° polarization-axis rotated splice[J]. Optics Express, 2010, 18(2): 1677-1683.

[12] Yu Xu-hui, Ma Hui-lian, Jin Zhong-he, et al. Improving thermal stability of a resonator fiber optic gyro employing a polarizing resonator[J]. Optics Express, 2013, 21(1): 358-369.

Rapid modeling and compensation method for scale factor of FOG with continuous rotation

ZHANG Xiao-ya, YANG Zhi-huai, SONG Li-wei, Ma Lin

(Tianjin Navigation Instrument Research Institute, Tianjin 300131, China)

The scale-factor error is one of the major errors of FOG, especially when applied in full temperature. Its influences are more than those of bias error in large angular rate or high-precision applications, and therefore should be modeled and compensated in practical application. Based on the analysis of the scale factor’s error mechanism, a modeling and compensation method for FOG scale-factor in full-temperature is presented based on a continuous rotation method, which is easier and more efficient. More importantly, the inflection points can be obtained effectively, and the precisions of the modeling and compensation will be improved. Experiment results show that the real inflection point, which is 48℃, of a certain type of FOG can be accurately measured. The compensation accuracy of scale factor error by this modeling method is better than 15×10-6, which is improved by about 10%.

fiber optic gyro; scale factor; temperature modeling; compensation

U666.1

A

1005-6734(2016)02-0215-03

10.13695/j.cnki.12-1222/o3.2016.02.014

2015-12-10

2016-03-23

國防預研項目（51309010102）

張曉雅（1981—），男，高級工程師，研究方向為導航、制導與控制。E-mail: zhangxy1208@163.com