升降速過程中轉子系統油膜失穩規律*

馬 輝， 王雪玲， 牛和強， 李 輝

(東北大學機械工程與自動化學院 沈陽，110819)

升降速過程中轉子系統油膜失穩規律*

馬 輝， 王雪玲， 牛和強， 李 輝

(東北大學機械工程與自動化學院 沈陽，110819)

以某懸臂轉子-軸承系統為研究對象，基于有限元方法建立了轉子-軸承系統動力學模型。通過時域圖、三維譜圖和幅頻響應圖得到了轉子系統升降速過程中出現的油膜失穩特征，分析了不同角加速度值在升降速過程中對1階和2階油膜失穩規律的影響。研究發現：升降速過程中產生的切向慣性力會改變油膜失穩轉速，與穩態情況(角加速度為零)相比，升降速情況下2階油膜失穩轉速有所延遲；升速過程中隨著角加速度值的增大2階油膜失穩轉速略有增加、降速過程略有減??；降速過程與升速過程相比，出現明顯的遲滯效應。

升降速; 轉子-軸承系統； 滑動軸承； 油膜振蕩； 有限元

引 言

隨著旋轉機械向高轉速、大跨度和柔性輕結構方向發展，滑動軸承油膜與轉子相互作用引起的油膜失穩問題日益突出。高速旋轉機械高階油膜失穩的研究對于旋轉機械設計以及應用具有重要意義。

在滑動軸承的非線性油膜力模型的研究方面，Muszynska等[1]提出了一個基于流體圓周平均流速的非線性油膜力模型，基于實驗驗證了此模型能夠預測轉子-密封系統的失穩問題?；凇盁o限短”軸承的假設，Capone[2-3]提出了動態油膜力模型，計算結果表明具有良好的精度和收斂性。劉長利等[4]在Capone油膜力的基礎上，對裂紋和油膜耦合故障轉子周期運動分岔做了分析。以上兩種模型忽略了非穩態項對油膜邊界的影響，Zhang等[5]提出一種非穩態油膜力模型，研究了轉子偏心對系統失穩的影響，并與穩態油膜力模型進行了對比，結果顯示非穩態油膜力模型更接近工程實際。張彥梅等[6]指出非穩態油膜力模型可能更適用于大擾動的非線性轉子動力學研究，并與穩態油膜力模型進行對比分析。

在滑動軸承導致的油膜失穩研究方面，Ma等[7]研究了雙盤轉子系統不同相位角在穩態情況下對于2階油膜失穩的影響。Wan等[8]研究了多盤轉子系統聯軸器不對中轉子系統的非線性動力特性，研究發現不對中可以延遲油膜振蕩的發生，降低振蕩幅值。EI-Shafei等[9]建立了一個懸臂柔性轉子系統，通過實驗分別研究了不同不平衡量、油壓及不對中條件對轉子系統失穩的影響。

旋轉機械的升降速過程中需要引入角加速度的慣性效應。de Castro等[10]建立一個中心圓盤的不平衡水平和垂直轉子系統，引入角加速度因素，在短軸承假設的基礎上研究了轉子系統在升降速過程的動態特性。Jing等[11]基于連續質量模型研究了轉子-軸承系統的動態特性及轉子系統的升降速過程中出現的遲滯效應。

可見，國內外學者對轉子系統的升降速過程進行了系統研究，但對于在升降速過程中角加速度對2階油膜失穩影響關注較少。筆者以文獻[9]的懸臂轉子-軸承系統為研究對象，在建模中引入角加速度影響因素，采用Newmark-β數值積分法，分析了角加速度在懸臂轉子-軸承系統升降速過程中對油膜失穩轉速的影響及系統復雜非線性動力學特性。

1 有限元模型及模型驗證

為了更好地模擬分析轉子系統模型的動力學特性，根據以下假設對系統進行簡化：a.轉軸采用Timoshenko梁進行模擬,盤模型以集中質量疊加到對應的節點上;b.左、右滑動軸承均采用文獻[5]的非線性非穩態油膜力模型來模擬[5]。

軸段單元有限元模型如圖1所示。其中：x,y以及θx,θy分別為橫向位移和旋轉方向的角位移；下標A和B分別為節點A和B。轉軸的梁單元位移向量ue表示為

(1)

其中:上標e表示每個有限元單元;每個梁單元的質量、剛度和陀螺矩陣分別表示為Me,Ke和Ge(詳見文獻[12])。

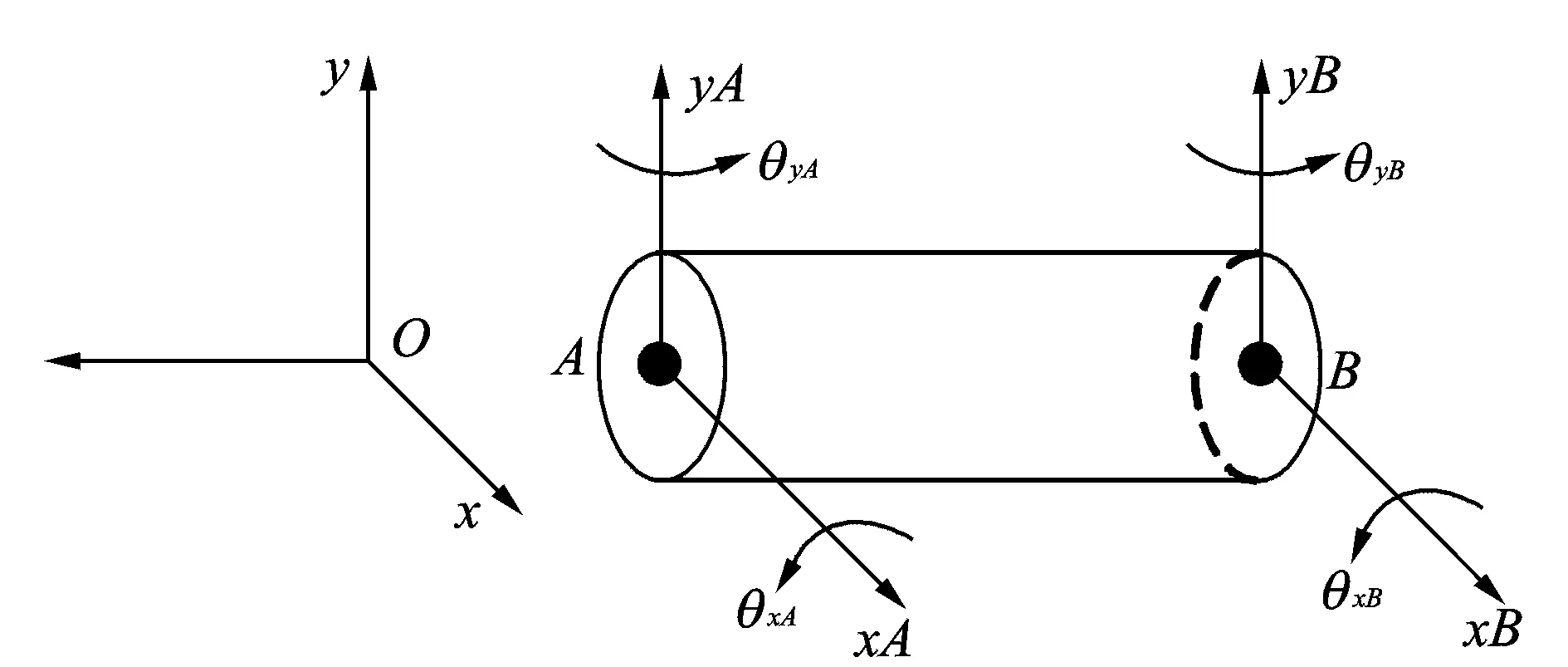
圖1 軸段單元有限元模型Fig.1 The finite element model of the shaft element

該轉子-軸承系統運動方程為

(2)

(3)

其中：M為質量矩陣；G為陀螺矩陣；C為阻尼矩陣；K為剛度矩陣；q為位移向量；Fu，Fb和Fg分別為轉盤產生的激振力及升降速的慣性力、軸承油膜力和重力外激勵向量；θ為系統的轉角。

筆者采用瑞利阻尼來描述系統阻尼，表達式為

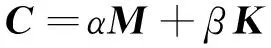
(4)

(5a)

(5b)

其中：ωn1和ωn2分別為系統的1階和2階固有角頻率(r/min)；ξ1和ξ2分別為系統的1階和2階模態阻尼比。

基于短軸承理論，張文等[5]提出的非穩態油膜力模型為

(6)

(7)

其中：η為潤滑油黏度；L，D和c分別為滑動軸承長度、直徑和平均直徑間隙；無量綱油膜力fbx和fby的表達式詳見文獻[5]。

為了驗證仿真計算的有效性，選用文獻[10]中相同的模型參數，取降速的角加速度值為3 πrad/s2，仿真結果與文獻結果對比如圖2所示?？梢钥闯觯抡婺Ｐ?階油膜失穩頻率為21.82 Hz，油膜失穩轉速為2 203.8 r/min，這些仿真結果和文獻中的實驗結果(22 Hz和2 160 r/min)基本一致，可見本研究數值仿真方法的有效性。

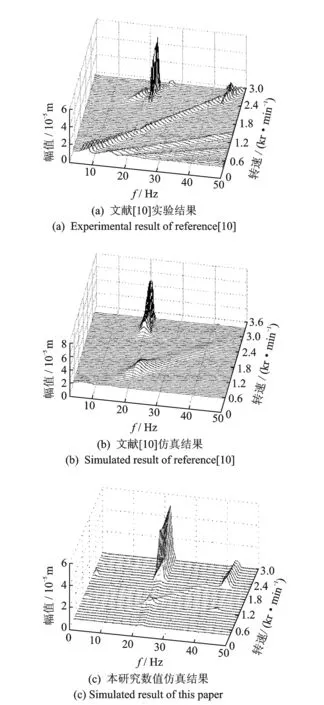
圖2 本研究仿真結果和文獻[10]實驗結果、仿真結果三維譜圖對比Fig.2 The spectrum cascades comparison among the simulation results of this paper, the simulation and experiment results of reference [10]

2 角加速度對油膜失穩影響

2.1 懸臂轉子系統有限元模型建立

文獻[9]中的懸臂轉子-軸承系統結構尺寸如圖3所示。4個盤的結構及質量相同，其他仿真參數如表1所示。當懸臂轉子系統左右軸承均采用彈簧阻尼模型，支撐剛度和阻尼分別取k=2×108N/m，c=2×103N·s/m時，通過計算得到該懸臂轉子系統的1階和2階臨界轉速分別為1 637.37 r/min和4 112.74 r/min，與文獻[9]中提到的1階和2階臨界轉速(1 680 r/min和4 171 r/min)的實驗結果相近。

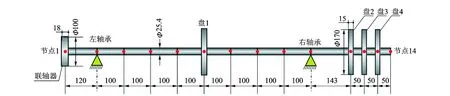
圖3 懸臂轉子-軸承系統結構尺寸、節點及單元示意圖(單位：mm)Fig.3 Schematic of the overhung rotor-bearing system, nodes and elements(unit:mm)

Tab.1 Model simulation parameters of the rotor-bearing system

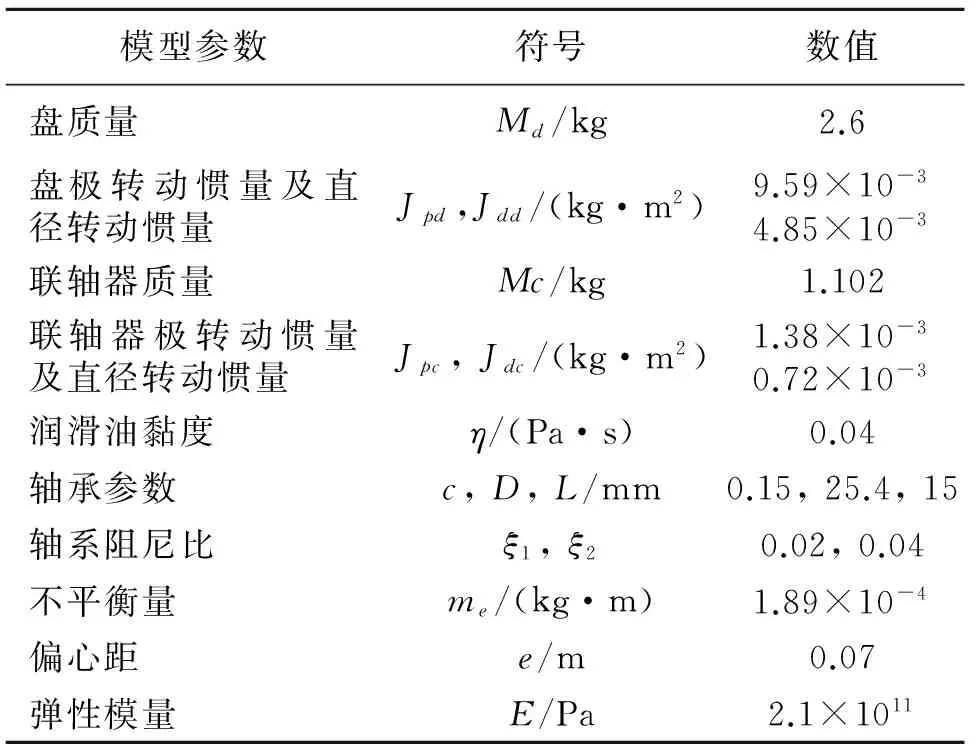
模型參數符號數值盤質量Md/kg2.6盤極轉動慣量及直徑轉動慣量Jpd,Jdd/(kg·m2)9.59×10-34.85×10-3聯軸器質量Mc/kg1.102聯軸器極轉動慣量及直徑轉動慣量Jpc,Jdc/(kg·m2)1.38×10-30.72×10-3潤滑油黏度η/(Pa·s)0.04軸承參數c,D,L/mm0.15,25.4,15軸系阻尼比ξ1,ξ20.02,0.04不平衡量me/(kg·m)1.89×10-4偏心距e/m0.07彈性模量E/Pa2.1×1011

2.2 數值計算及理論分析

假定僅在盤1存在偏心。升降速過程的勻角加速度α范圍為25～125 rad/s2，取值間隔為25 rad/s2。通過分析穩態和升降速的三維譜圖(限于篇幅，僅給出角加速度值為0，25和125 rad/s2情況下的三維譜圖)，分析5種角加速度值在升降速過程中的1階和2階油膜失穩轉速，得到不同角加速度值下的1階和2階油膜失穩轉速規律曲線，如圖4所示。圖中，P1和P2兩點為穩態情況下1階和2階油膜失穩轉速(見圖5)，其值分別為3 625 r/min和8 125 r/min。

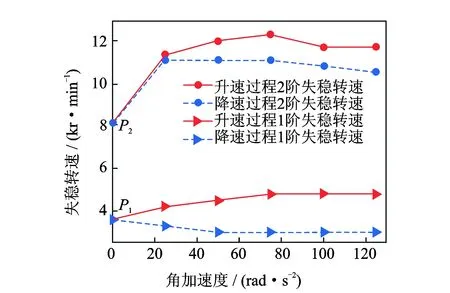
圖4 油膜失穩轉速-角加速度規律曲線Fig.4 The oil film unstable thresholds curve with different angular accelerations

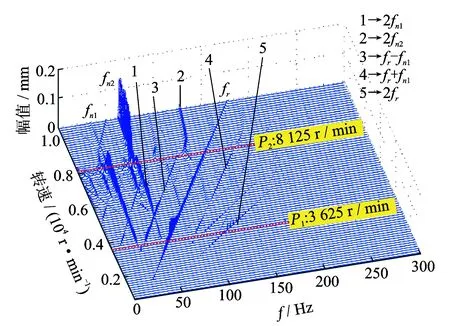
圖5 右軸承豎直方向穩態響應三維譜圖(α=0)Fig.5 The spectrum cascade of vertical stable responses of the right bearing (α=0)

從圖4可以看出，在升速過程中，當角加速度增加時，1階油膜失穩轉速較穩態油膜失穩轉速不斷向后推移并趨于平穩。當α∈(25,75) rad/s2時，2階油膜失穩比例有增大的趨勢；當α∈(75,125) rad/s2時，2階失穩比例有減小的趨勢。降速過程中出現明顯的渦動現象，1階油膜失穩轉速較穩態有所提前，并且明顯滯后于升速過程，即出現了遲滯效應。當α∈(25,125) rad/s2時，2階油膜失穩轉速在10 810±300 r/min范圍變化，趨勢較為平穩。

不同角加速度情況下的三維譜圖如圖6所示。由圖可知，在升降速過程中出現的頻率成分包括1階油膜振蕩頻率fn1、2階油膜振蕩頻率fn2和轉頻fr，及組合頻率成分2fn2，fr-2fn2，fr-fn1和fr+fn1等。當角加速度α=25 rad/s2時，升速過程中1階和2階油膜失穩轉速分別為4 206 r/min 和11 410 r/min；降速過程中對應值分別為3 306 r/min和11 110 r/min。當角加速度α=125 rad/s2時，升速過程中1階和2階油膜失穩轉速分別為4 806 r/min 和11 710 r/min；降速過程中對應值分別為3 006 r/min和10 510 r/min。

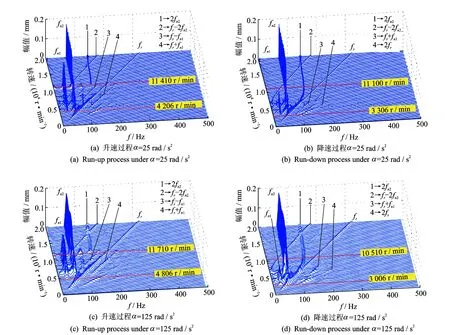
圖6 右軸承豎直方向升降速響應三維譜圖Fig.6 The spectrum cascades of vertical responses of the right bearing during the run-up and run-down processes

做角加速度值為25，125 rad/s2右軸承處升降速過程時域波形如圖7所示。從時域圖看出，由于慣性效應的存在，在滯后于1階和2階固有頻率處有明顯的共振峰，并且角加速度值為125 rad/s2的共振時間明顯短于角加速度值為25 rad/s2的時間。

右軸承處升降速過程的幅頻響應曲線如圖8所示。通過對比發現，整體看降速過程的油膜失穩轉速和升速過程的油膜失穩轉速有明顯遲滯特性，即油膜失穩轉速并沒有在升速過程出現失穩位置消失，而是降速到更低的轉速時失穩現象才消失。

油膜對軸頸的總壓力在垂直于偏心距方向存在一個導致油膜失穩的切向分力[13]。升降速過程中的1階和2階油膜失穩轉速與穩態油膜穩轉速產生差異的原因可能是由于在升降速過程中產生的切向慣性力，影響了油膜的失穩規律。

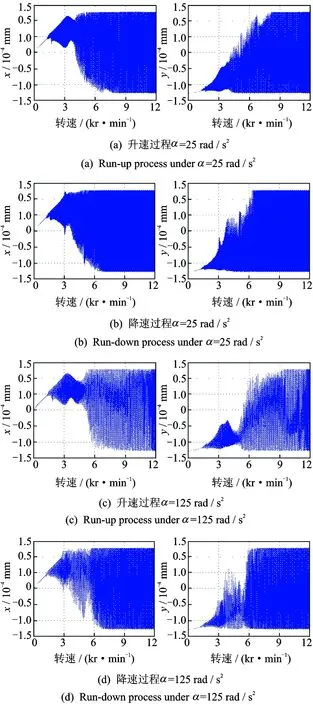
圖7 右軸承水平和豎直方向升降速位移時域波形Fig.7 The time-domain displacement waveforms of the right bearing in horizontal and vertical directions

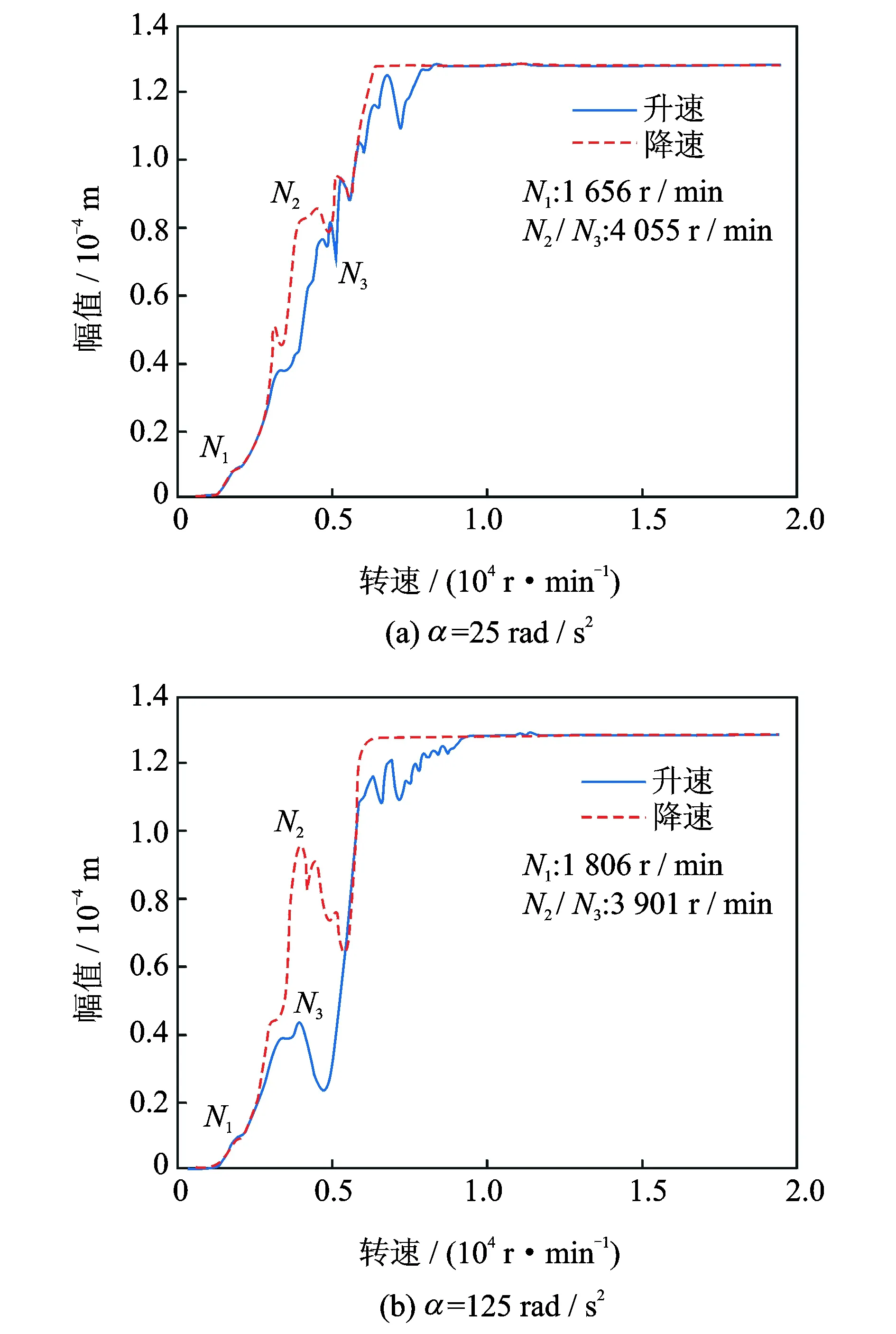
圖8 升降速幅頻響應曲線Fig.8 The amplitude-frequency responses of rotor system during the run-up and run-down processes

3 結 論

1) 升速過程和穩態情況相比，系統的1階和2階油膜失穩轉速有所推遲。在筆者研究的角加速度范圍內，油膜失穩轉速隨著角加速度值的增大而增加并趨于平穩，并且2階的油膜失穩轉速變化幅度大于1階。

2)降速過程中，由于慣性效應的存在，系統的1階油膜失穩轉速較穩態有所提前，2階油膜失穩轉速較穩態有所推遲，失穩時間延長。此外，降速過程相對于升速過程而言，1階和2階油膜失穩并沒有在轉速降低到升速過程中出現失穩的轉速位置消失，而是降低到更低的轉速失穩才消失，即出現了遲滯效應。

[1] Muszynska A, Bently D E. Anti-swirl arrangements prevent rotor/seal instability[J]. Journal of Vibration Acoustics Stress and Reliability in Design, 1989,111:156-161.

[2] Capone G. Orbital motions of rigid symmetric rotor supported on journal bearings[J]. La Meccanica Italiana, 1986,199(199):37-46.

[3] Capone G. Analytical description of fluid-dynamic force field in cylindrical journal bearing[J]. L′Energia Elettrica, 1991,3(3):105-110.

[4] 劉長利,夏春明,鄭建榮,等.裂紋和油膜耦合故障轉子周期運動分岔分析[J].振動、測試與診斷,2008,28(1):35-38.

Liu Changli, Xia Chunming, Zheng Jianrong, et al. Study on bifurcation of periodic motion of rotor system with crack and oil whirl fault[J]. Journal of Vibration, Measurement & Diagnosis, 2008,28(1):35-38. (in Chinese)

[5] Zhang Wen, Xu Xiaofeng. Modeling of nonlinear oil-film force acting on a journal with unsteady motion and nonlinear instability analysis under the model[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2000,1(3):179-186.

[6] 張彥梅, 陸啟韶.一種非穩態油膜力模型下轉子系統的碰摩分岔分析[J].振動工程學報,2002,15(1):68-73.

Zhang Yanmei, Lu Qishao. Impact bifurcate analysis on a bearing-rotor system with unsteady oil film forces[J]. Journal of Vibration Engineering, 2002,15(1):68-73. (in Chinese)

[7] Ma Hui, Li Hui, Zhao Xueyan, et al. Effects of eccentric phase difference between two discs on oil-film instability in a rotor-bearing system[J]. Mechanical Systems and Signal Processing, 2013,41(1):526-545.

[8] Wan Zhao, Jing Jianping, Meng Guang, et al. Theoretical and experimental study on the dynamic response of multi-disk rotor system with flexible coupling misalignment[J]. Journal of Mechanical Engineering Science, 2012,226:2874-2886.

[9] El-Shafei A, Tawfick S H, Raafat M S, et al. Some experiments on oil whirl and oil whip[J]. Journal of Engineering for Gas Turbines and Power, 2007, 129(1):144-153.

[10]de Castro H F, Cavalca K L, Nordmann R. Whirl and whip instabilities in rotor-bearing system considering a nonlinear force model[J]. Journal of Sound and Vibration, 2008,317(1):273-293.

[11]Jing Jianping, Meng Guang, Sun Yi, et al. On the oil-whipping of a rotor-bearing system by a continuum model[J]. Applied Mathematical Modelling, 2005,29(5):461-475.

[12]Ma Hui, Yang Jian, Song Rongze, et al. Effects of tip relief on vibration responses of a geared rotor system[J]. Journal of Mechanical Engineering Science, 2014,228(7):1132-1154.

[13]鐘一諤,何衍宗,壬正，等.轉子動力學[M].北京:清華大學出版社，1987:63-68.

航空發動機振動監測和分析系統研制成功

森德格公司(sendig.com.cn)，經過多年的研究和大量現場試驗，在近期成功發布了系列化航空發動機振動監測和分析儀器產品。包括有：SAVT-1H小型手持式振動測量儀器，可測量發動機的多種通頻振值；SAVT-2H航空發動機振動分析儀和動平衡儀，可測量多種振值、波形、頻譜。同時配有設備狀態監測及趨勢分析軟件和故障診斷專家系統，可以自動生成各種報告；SAVT-5航空發動機振動變送器，是為連續監測發動機振動值的在線監測儀表，可以在駕駛艙實時顯示振值，并在振值超標時立即報警以避免重大事故的發生。

SAVT系列儀器已經過生產廠家臺架和外場實機的多次成功考驗，填補了我國飛行器發動機振動監測和分析儀器缺少自主知識產權產品的空白。

10.16450/j.cnki.issn.1004-6801.2016.01.009

??人才支持計劃資助項目(NCET-11-0078)

2014-01-10；修回日期：2014-03-04

TH113.1

馬輝，男，1978年9月生，博士、副教授。主要研究方向為旋轉機械動力學與故障診斷領域的理論與技術應用。曾發表《Effects of eccentric phase difference between two discs on oil-film instability in a rotor-bearing system》(《Mechanical Systems and Signal Processing》2013，Vol.41,No.1-2)等論文。 E-mail：huima@me．neu．edu．cn