基于穩(wěn)健回歸分析的轉(zhuǎn)子系統(tǒng)不平衡量識別*
臧廷朋, 溫廣瑞,2,3, 廖與禾
(1.西安交通大學(xué)現(xiàn)代設(shè)計(jì)與轉(zhuǎn)子軸承系統(tǒng)教育部重點(diǎn)實(shí)驗(yàn)室 西安, 710049) (2.西安交通大學(xué)機(jī)械結(jié)構(gòu)強(qiáng)度與振動國家重點(diǎn)實(shí)驗(yàn)室 西安, 710049) (3.新疆大學(xué)機(jī)械工程學(xué)院 烏魯木齊, 830047)
基于穩(wěn)健回歸分析的轉(zhuǎn)子系統(tǒng)不平衡量識別*
臧廷朋1, 溫廣瑞1,2,3, 廖與禾1
(1.西安交通大學(xué)現(xiàn)代設(shè)計(jì)與轉(zhuǎn)子軸承系統(tǒng)教育部重點(diǎn)實(shí)驗(yàn)室 西安, 710049) (2.西安交通大學(xué)機(jī)械結(jié)構(gòu)強(qiáng)度與振動國家重點(diǎn)實(shí)驗(yàn)室 西安, 710049) (3.新疆大學(xué)機(jī)械工程學(xué)院 烏魯木齊, 830047)
不平衡是造成轉(zhuǎn)子系統(tǒng)振動過大、影響其安全運(yùn)行的重要因素。傳統(tǒng)的最小二乘算法(least squares, 簡稱LS)在不平衡量識別過程中存在對外界干擾或異常值敏感的問題,改進(jìn)的加權(quán)最小二乘算法(weighted least squares, 簡稱WLS)雖然能夠降低異常值的影響,但需要經(jīng)驗(yàn)積累并對振動數(shù)據(jù)進(jìn)行深入分析。提出一種基于穩(wěn)健回歸分析的轉(zhuǎn)子系統(tǒng)不平衡量識別方法,通過構(gòu)建優(yōu)化的目標(biāo)函數(shù)自動消除異常值的影響,得到正常狀態(tài)下轉(zhuǎn)子系統(tǒng)不平衡量的最佳估值。實(shí)驗(yàn)結(jié)果表明,該方法能夠有效消除外界干擾和異常值的影響,準(zhǔn)確識別出轉(zhuǎn)子系統(tǒng)不平衡量。
穩(wěn)健回歸分析; 轉(zhuǎn)子; 最小二乘法; 不平衡
引 言
轉(zhuǎn)子動平衡技術(shù)是減小機(jī)組振動和保障機(jī)組安全平穩(wěn)運(yùn)行的重要手段。目前,已形成以影響系數(shù)法和模態(tài)平衡法為核心的眾多成熟技術(shù)[1-4],國內(nèi)外的相關(guān)研究集中以提高平衡效率為目的。李常有等[5]通過研究系統(tǒng)的不平衡響應(yīng)與模型等效載荷的關(guān)系,提出了一種基于模型的轉(zhuǎn)子系統(tǒng)不平衡量估計(jì)方法,該方法利用模態(tài)擴(kuò)展技術(shù)可以準(zhǔn)確識別不平衡量的大小和位置。Saldarriaga等[6]從反問題的角度出發(fā),利用基于遺傳算法的偽隨機(jī)優(yōu)化方法模擬轉(zhuǎn)子系統(tǒng)的不平衡響應(yīng),實(shí)現(xiàn)不平衡量的識別。上述研究都是以準(zhǔn)確獲得振動數(shù)據(jù)為基礎(chǔ),但在噪聲干擾較大等的惡劣工業(yè)環(huán)境中推廣應(yīng)用受到很大限制。
實(shí)際平衡過程中通常利用最小二乘法或加權(quán)最小二乘法等優(yōu)化算法實(shí)現(xiàn)轉(zhuǎn)子系統(tǒng)不平衡量的識別。最小二乘法對轉(zhuǎn)子不平衡響應(yīng)的誤差分布有嚴(yán)格要求,當(dāng)誤差不滿足正態(tài)分布或測量數(shù)據(jù)存在異常值時,不能準(zhǔn)確完成系統(tǒng)不平衡量的識別[7]。加權(quán)最小二乘算法通過分配不同的權(quán)重系數(shù)能夠有效消除外界干擾的影響,但需要操作者具有豐富的經(jīng)驗(yàn)并對振動數(shù)據(jù)進(jìn)行深入分析。近年來,先進(jìn)的動平衡技術(shù)特別是快速高效動平衡和自動平衡技術(shù)[8]的出現(xiàn)和發(fā)展對轉(zhuǎn)子系統(tǒng)不平衡量識別的穩(wěn)健性提出了更高的要求。
筆者利用穩(wěn)健回歸分析方法實(shí)現(xiàn)復(fù)雜環(huán)境下轉(zhuǎn)子系統(tǒng)的不平衡量識別。該方法能夠克服最小二乘法對測量數(shù)據(jù)異常值敏感的問題,提高不平衡量識別過程的穩(wěn)健性。能夠依據(jù)不平衡響應(yīng)的分布特性自動分配不同的權(quán)重系數(shù),減小對專家經(jīng)驗(yàn)的依賴。通過實(shí)驗(yàn)驗(yàn)證了基于穩(wěn)健回歸分析的轉(zhuǎn)子系統(tǒng)不平衡量識別方法的有效性和實(shí)用性。
1 影響系數(shù)法及回歸分析模型
影響系數(shù)法是建立在線性振動理論基礎(chǔ)上的一種平衡方法,因其原理清晰、操作簡單而廣泛應(yīng)用于轉(zhuǎn)子系統(tǒng)平衡[9]。M個平衡面、N個測振點(diǎn)、單一平衡轉(zhuǎn)速時影響系數(shù)的平衡方程為
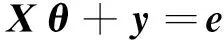
(1)
矩陣形式表達(dá)為
(2)
其中:X為影響系數(shù)矩陣;aij為j平衡面對i測點(diǎn)的影響系數(shù);θj為j平衡面的配重質(zhì)量;yi為i測點(diǎn)的不平衡響應(yīng);ei為i測點(diǎn)的殘余振動。
(3)
式(3)可以轉(zhuǎn)換為多元回歸分析問題[10]
(4)
2 穩(wěn)健回歸分析
穩(wěn)健回歸分析的主要思想是通過對異常值敏感的最小二乘回歸中的目標(biāo)函數(shù)進(jìn)行優(yōu)化,選擇適當(dāng)?shù)臋?quán)重函數(shù)盡可能地降低異常值對參數(shù)估值的影響,得到存在外界干擾情況下的最佳估值。根據(jù)異常點(diǎn)的類型,回歸分析的穩(wěn)健性分別由失效點(diǎn)和影響函數(shù)度量。失效點(diǎn)定義為使估計(jì)量達(dá)到任意大時異常點(diǎn)的最小百分比,主要用來限制轉(zhuǎn)子系統(tǒng)不平衡響應(yīng)中外界干擾和異常值的影響。對于給定估計(jì)方法T,長度為n的有限元素序列Z的失效點(diǎn)為
(5)
其中:Z*為任意改變Z中p個元素值所組成的序列。
由于單個異常值能夠使LS產(chǎn)生任意大的估計(jì)值,因此LS的失效點(diǎn)為0,而穩(wěn)健回歸分析的失效點(diǎn)最高可達(dá)50%。
影響函數(shù)用來度量轉(zhuǎn)子系統(tǒng)影響系數(shù)矩陣中泄漏點(diǎn)對回歸分析的局部影響,通常利用帽子矩陣H對角線值進(jìn)行衡量
(6)
目前,穩(wěn)健回歸分析已經(jīng)發(fā)展多種不同的估計(jì)方法,筆者主要研究M-Huber估計(jì)、MM估計(jì)以及最小二乘中位數(shù)(least median of squares, 簡稱LMS)估計(jì)在轉(zhuǎn)子系統(tǒng)不平衡量識別中的應(yīng)用。
2.1 M-Huber估計(jì)
M估計(jì)是最大似然估計(jì)的擴(kuò)展和推廣,由Huber于1981年提出[11],通過一個遞增速率較低的殘差函數(shù)代替最小二乘回歸中殘差平方和函數(shù)實(shí)現(xiàn)回歸穩(wěn)健性的提高。
(7)
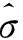
M估計(jì)的目標(biāo)函數(shù)不具備尺度同變性,需要利用尺度參數(shù)對殘差進(jìn)行標(biāo)準(zhǔn)化處理,常用中位絕對離差(medianabsolutedeviation, 簡稱MAD)對殘差的尺度參數(shù)進(jìn)行穩(wěn)健估計(jì)。
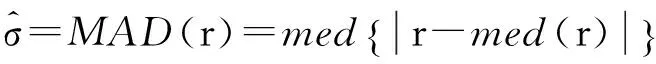
(8)
其中:med為計(jì)算序列的中位數(shù)。
M-Huber是M類估計(jì)中常用的一種估計(jì),其目標(biāo)函數(shù)為

(9)
其中:k為調(diào)整系數(shù),較小的k值能產(chǎn)生較大的穩(wěn)健性,在綜合考慮穩(wěn)健性和計(jì)算效率的情況下通常取k=1.345。
2.2LMS估計(jì)
最小二乘中位數(shù)估計(jì)利用殘差平方的中位數(shù)替換最小二乘估計(jì)中的殘差平方和
(10)
殘差平方的中位數(shù)相比殘差平方和更為穩(wěn)健,估計(jì)結(jié)果能更好地抵抗干擾和特異值的影響,失效點(diǎn)最高可達(dá)50%,但較低的計(jì)算效率限制了該估計(jì)的廣泛應(yīng)用。
2.3MM估計(jì)
MM估計(jì)使用一種以上的M估計(jì)來計(jì)算最終的估計(jì)值,具有高穩(wěn)健性優(yōu)點(diǎn)的同時還保留了M類估計(jì)運(yùn)算效率高的特點(diǎn)[12],因而成為目前應(yīng)用最多的穩(wěn)健估計(jì)方法。MM估計(jì)的目標(biāo)函數(shù)采用Tukey雙核函數(shù)
(11)
當(dāng)調(diào)整系數(shù)k=4.685時,MM估計(jì)穩(wěn)健性較好,同時可以保持95%的估計(jì)效率。MM估計(jì)的求解通過迭代再加權(quán)最小二乘法(lterativelyreweightedleastsquares, 簡稱IRLS)實(shí)現(xiàn),步驟如下:
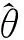
2) 通過M估計(jì)計(jì)算得到殘差r0尺度的穩(wěn)健估計(jì)sn;
4) 重復(fù)步驟2, 3,直到循環(huán)迭代滿足終止條件為止。
3 平衡實(shí)驗(yàn)
通過BentlyRK4轉(zhuǎn)子實(shí)驗(yàn)臺進(jìn)行基于穩(wěn)健回歸分析的不平衡量估計(jì)方法的驗(yàn)證。為了充分考慮轉(zhuǎn)子支撐各向異性的影響,分別在A,B兩測量面上安裝相互垂直的電渦流傳感器,實(shí)驗(yàn)臺結(jié)構(gòu)和傳感器的安裝方式如圖1所示。系統(tǒng)結(jié)構(gòu)下轉(zhuǎn)子的一階臨界轉(zhuǎn)速約為1 880 r/min。
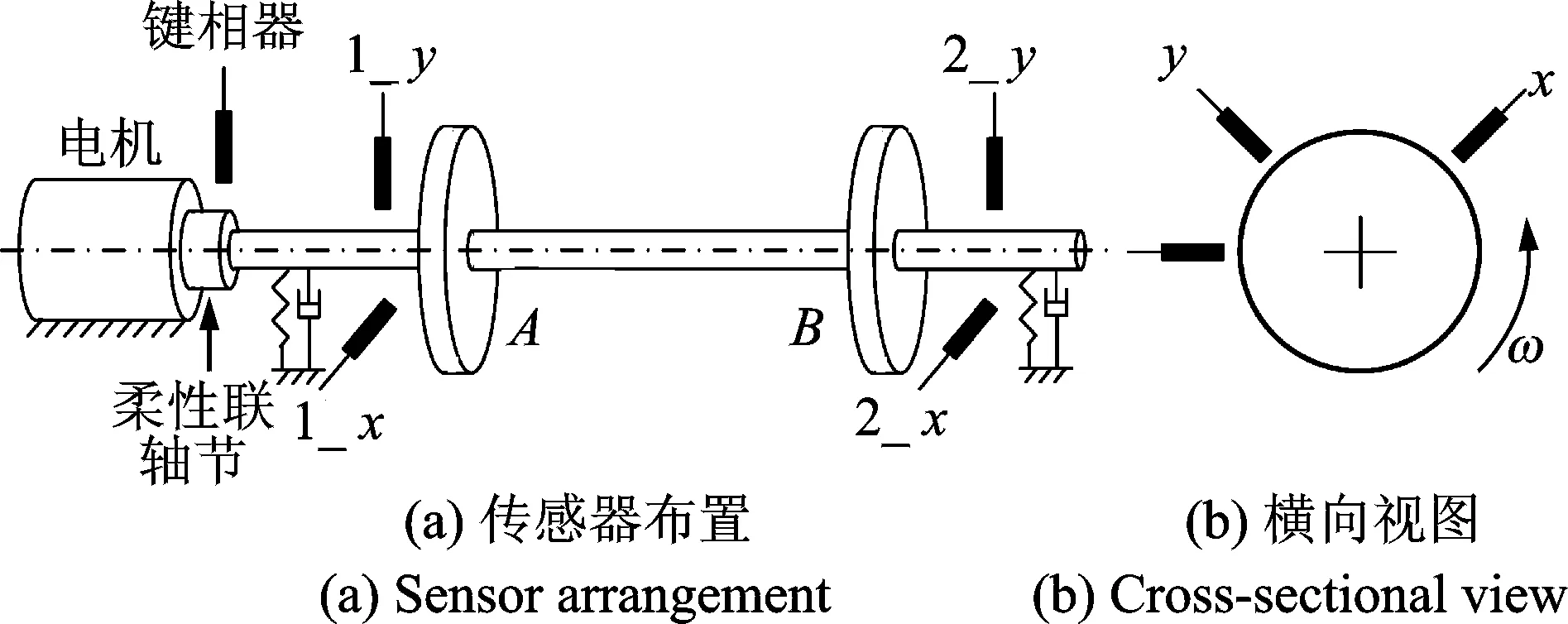
圖1 傳感器安裝示意圖Fig.1 The structure sketch of test rig
為了消除轉(zhuǎn)子非失衡故障對不平衡量估計(jì)的影響,通過一次停車過程記錄轉(zhuǎn)子系統(tǒng)原始狀態(tài)下的振動信息。在A平衡面0°位置添加0.4 g的不平衡量模擬失衡故障,通過一次起車過程獲得該狀態(tài)的振動信息。利用上述兩次過程獲得轉(zhuǎn)子系統(tǒng)在1 000~2 500 r/min范圍內(nèi)的不平衡量響應(yīng)如圖2所示。
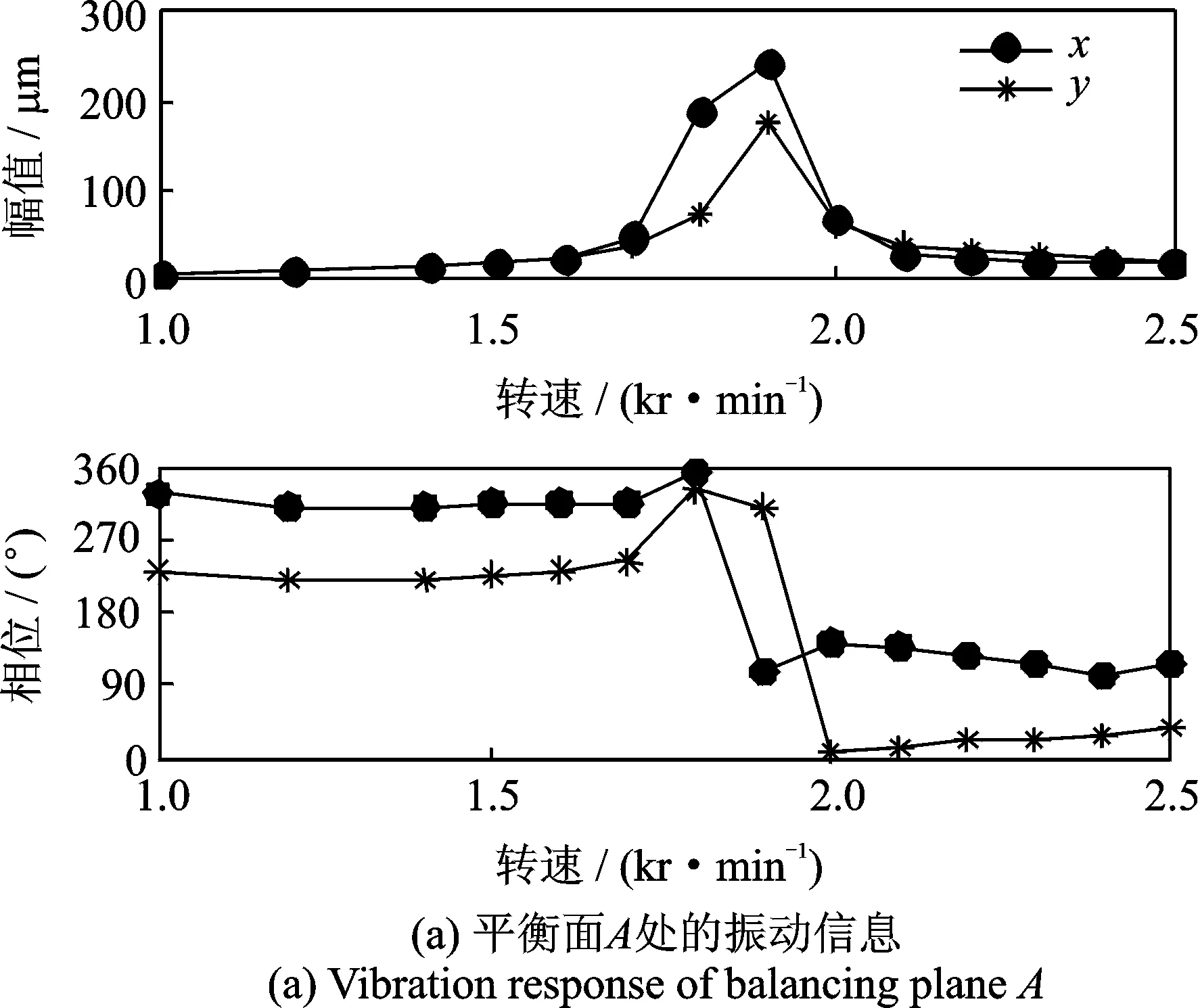
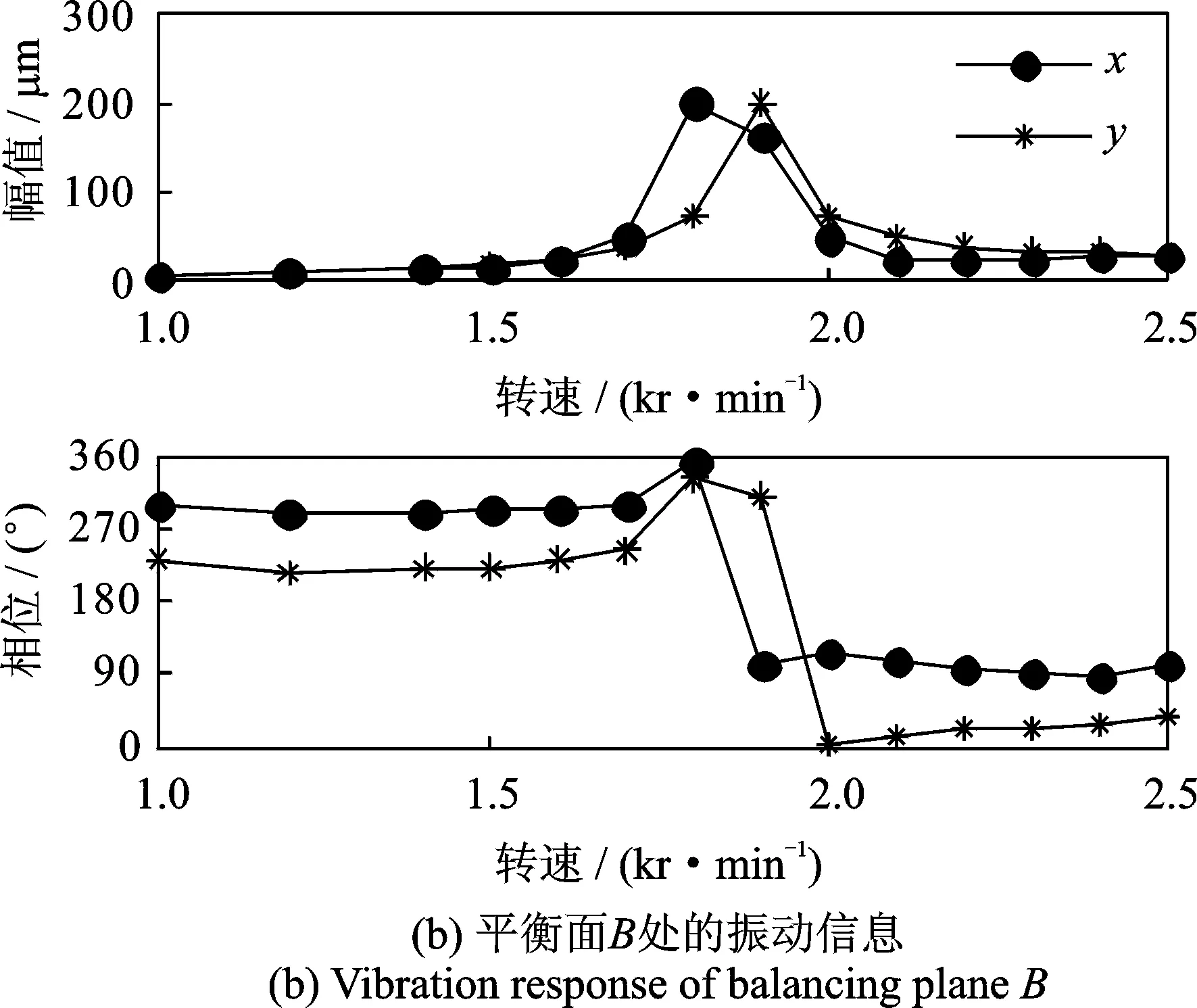
圖2 轉(zhuǎn)子系統(tǒng)不平衡量響應(yīng)Fig.2 Unbalance response of the rotor system
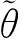
(12)
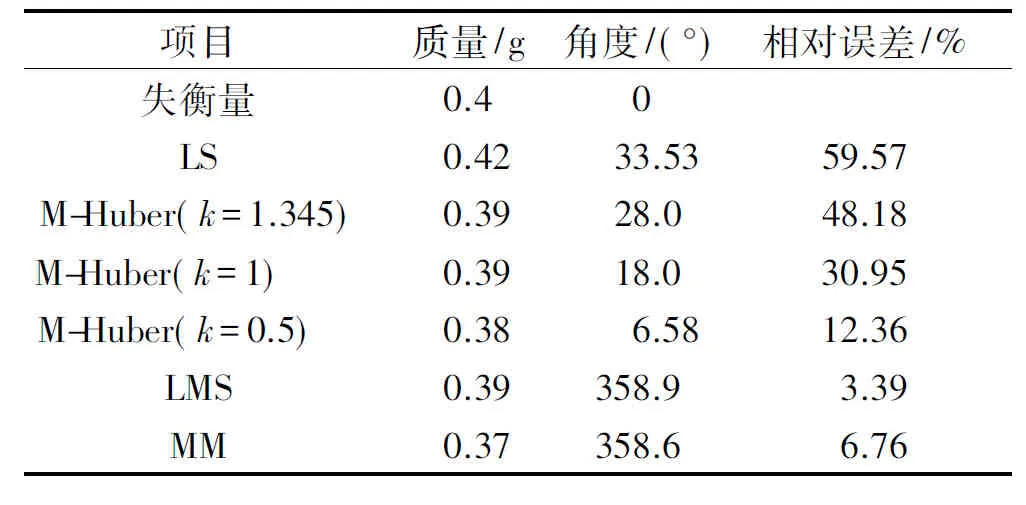
表1 不平衡量估計(jì)效果
從表1可以看出,穩(wěn)健回歸分析能夠比最小二乘法取得更好的不平衡量估計(jì)效果,相對誤差由最高的59.57%下降到最低的3.39%,不平衡量估計(jì)精度提升明顯,特別是相位估計(jì)精度的提高。對于M-Huber估計(jì)方法,隨著k值由1.345減小到0.5,即隨著穩(wěn)健程度的不斷提高,不平衡量的估計(jì)結(jié)果可以得到相同的結(jié)論。在綜合考慮計(jì)算效率和抗干擾能力時,基于穩(wěn)健MM估計(jì)的方法能夠取得較為理想的識別結(jié)果。
基于穩(wěn)健回歸分析的不平衡估計(jì)方法根據(jù)不平衡量響應(yīng)的殘差分布分配不同的權(quán)重系數(shù),本次實(shí)驗(yàn)中A,B截面的權(quán)重系數(shù)如圖3和圖4所示,其中虛線位置表示一階臨界轉(zhuǎn)速。由圖中可知,不同的穩(wěn)健回歸方法由于目標(biāo)函數(shù)的不同可能對相同的失衡響應(yīng)分配不同的權(quán)重系數(shù);所有的穩(wěn)健回歸方法都降低一階臨界轉(zhuǎn)速附近失衡響應(yīng)的權(quán)重系數(shù),與實(shí)際平衡中由于臨界轉(zhuǎn)速附近振動劇烈而難于獲得準(zhǔn)確的響應(yīng)一致。由圖3, 4及表1可以看出,穩(wěn)健回歸分析克服了最小二乘法對臨界轉(zhuǎn)速附近振動變化敏感的問題,根據(jù)系統(tǒng)不平衡響應(yīng)的分布特性自動分配的權(quán)重系數(shù)減小了對專家經(jīng)驗(yàn)的依賴,實(shí)現(xiàn)轉(zhuǎn)子系統(tǒng)多轉(zhuǎn)速多平面條件下的不平衡量的準(zhǔn)確估計(jì)。
4 結(jié)束語
討論了存在外界干擾或異常值的情況下轉(zhuǎn)子系統(tǒng)不平衡量識別的問題,提出了基于穩(wěn)健回歸分析的不平衡量識別方法。結(jié)果表明:a.M-Huber, LMS和MM等穩(wěn)健回歸分析方法能夠取得比最小二乘法更好的不平衡量識別精度,特別是相位的識別精度有明顯的提高;b.在綜合考慮計(jì)算效率和穩(wěn)健性程度的情況下,基于穩(wěn)健MM估計(jì)的方法能夠取得理想的不平衡量識別效果;c.與最小二乘法對不平衡響應(yīng)分配相同的權(quán)重系數(shù)不同,基于穩(wěn)健回歸分析的不平衡量識別方法降低一階臨界轉(zhuǎn)速附近不平衡響應(yīng)的系數(shù),與實(shí)際平衡中由于一階臨界轉(zhuǎn)速附近振動劇烈而難以準(zhǔn)確的失衡響應(yīng)一致。
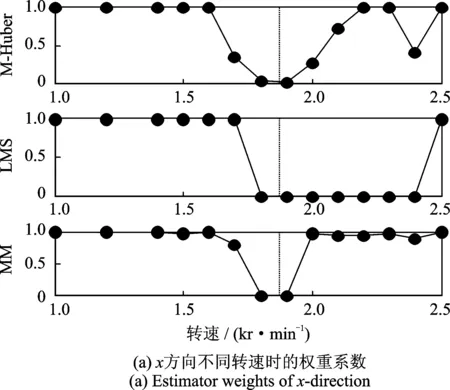
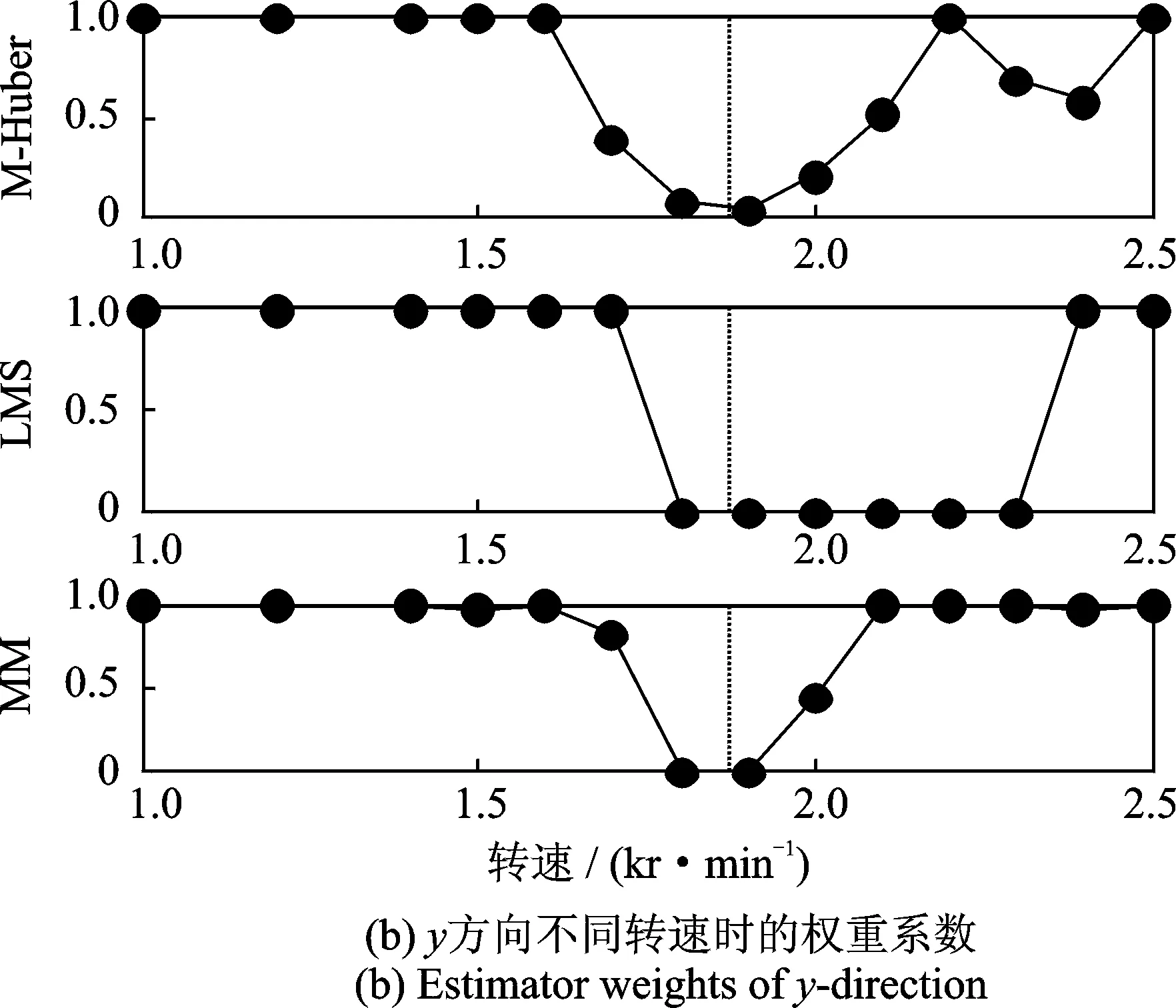
圖3 平衡面A權(quán)重系數(shù)分布Fig.3 Estimator weights of balancing plane A
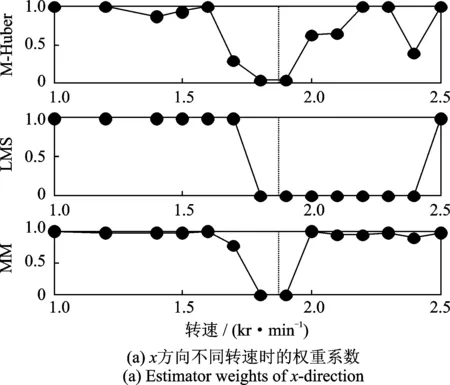
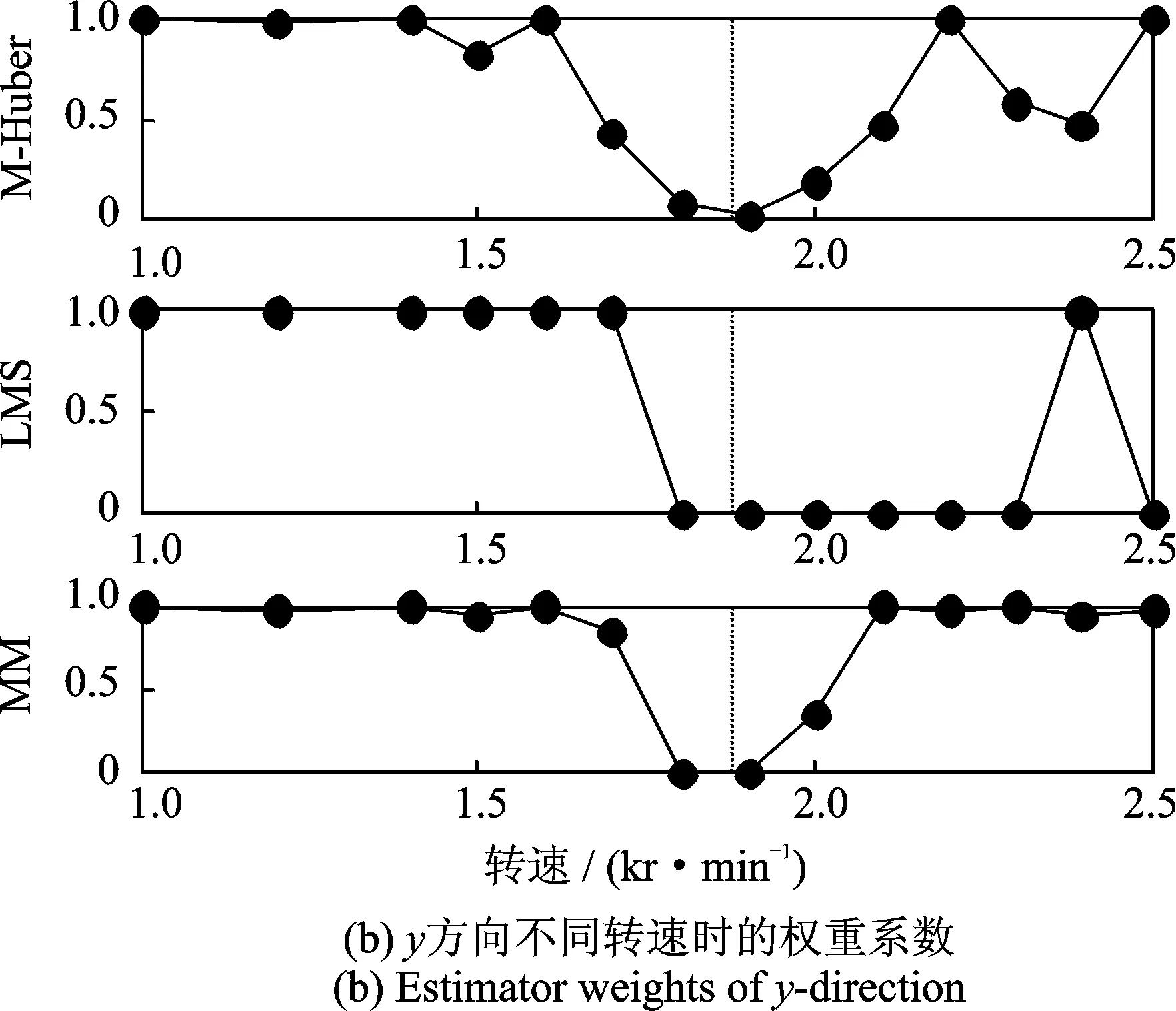
圖4 平衡面B權(quán)重系數(shù)分布Fig.4 Estimator weights of balancing plane B
[1] Goodman T P. A least-squares method for computing balance corrections [J]. Journal of Engineering for Industry, 1964, 86(3):273-277.
[2] Parkinson A G, Darlow M S, Smalley A J. A theoretical introduction to the development of a unified approach to flexible rotor balancing[J].Journal of Sound and Vibration, 1980, 68(4): 489-506.
[3] 繆紅燕,高金吉,徐鴻,等. 基于有限元法的柔性轉(zhuǎn)子虛擬動平衡研究[J]. 振動、測試與診斷, 2004,24(3):184-188.
Miao Hongyan, Gao Jinji, Xu Hong, et al. A study of virtual balancing of flexible rotor based on finite element method [J]. Journal of Vibration, Measurement & Diagnosis, 2004, 24(3):184-188.(in Chinese)
[4] 紀(jì)躍波. 弱非平穩(wěn)轉(zhuǎn)速下轉(zhuǎn)子動平衡方法[J]. 振動、測試與診斷, 2012, 32(4):596-601.
Ji Yuebo. Dynamic balancing of the rotor with weakly non-stationary rotational speed[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(4):596-601.(in Chinese)
[5] 李常有, 徐敏強(qiáng), 郭聳. 基于模型的轉(zhuǎn)子系統(tǒng)不平衡量的估計(jì)[J]. 航空動力學(xué)報(bào), 2009, 24(7):1530-1536.
Li Changyou, Xu MinQiang, Guo Song. Estimation of unbalance magnitude of rotor system based on model[J]. Journal of Aerospace Power, 2009, 24(7):1530 -1536.(in Chinese)
[6] Saldarriaga M V, Steffen V, Der Hagopian J, et al. On the balancing of flexible rotating machines by using an inverse problem approach [J]. Journal of Vibration and Control, 2011, 17(7):1021-1033.
[7] Pennacch P, Vania A, Bachschmid N. Increasing the
robustness of fault identification in rotor dynamics by means of m-estimators [J]. Mechanical Systems and Signal Processing, 2007, 21(8):3003-3029.
[8] 夏松波, 劉永光, 李勇,等. 旋轉(zhuǎn)機(jī)械自動動平衡綜述 [J]. 中國機(jī)械工程, 1999, 10(4):106-109.
Xia Songbo, Liu Yongguang, Li Yong, et al. A review on automatic balancing of rotating machinery [J]. China Mechanical Engineering, 1999, 10(4):106-109.(in Chinese)
[9] 陳敬平,嚴(yán)普強(qiáng).轉(zhuǎn)子現(xiàn)場動平衡的相對影響系數(shù)法[J].振動、測試與診斷, 1994, 14(4):1-6.
Chen Jingping, Yan Puqiang. Relative influence coefficient method-effective in field balancing of flexible rotors [J]. Journal of Vibration, Measurement & Diagnosis, 1994, 14(4):1-6.(in Chinese)
[10]Montgomery D C, Peck E A, Vining G G. Introduction to linear regression analysis [M]. New York: John Wiley & Sons, 2012:67-69.
[11]Huber P J. Robust statistics [M]. New York: Wiley, 1981:43-54.
[12]Yohai V J. High breakdown-point and high efficiency robust estimates for regression [J]. The Annals of Statistics, 1987, 15(2): 642-656.
[13]Pennacchi P, Chatterton S, Ricci R. Rotor balancing using high breakdown-point and bounded -influence estimators [J]. Mechanical Systems and Signal Processing, 2010, 24(3):860-872.

10.16450/j.cnki.issn.1004-6801.2016.01.021
*國家自然科學(xué)基金資助項(xiàng)目(51365051);教育部新世紀(jì)優(yōu)秀人才計(jì)劃資助項(xiàng)目(NCET-13-0461);中國博士后科學(xué)基金資助項(xiàng)目(2012M521758);學(xué)校博士學(xué)科點(diǎn)專項(xiàng)科研基金資助項(xiàng)目(20120201120043);基本科研業(yè)務(wù)經(jīng)費(fèi)資助項(xiàng)目
2014-03-27;修回日期:2014-11-21
TH17
臧廷朋,男,1985年12月生,博士研究生。主要研究方向?yàn)樾D(zhuǎn)機(jī)械故障診斷和轉(zhuǎn)子動平衡技術(shù)。曾發(fā)表《基于非平穩(wěn)信息的轉(zhuǎn)子瞬態(tài)動平衡方法》(《振動、測試與診斷》2013年第33卷第4期)等論文。 E-mail:zangtingpeng@126.com

