重卡駕駛室半主動懸置控制方法*

黃山云, 陳 彬， 涂奉臣， 陳照波， 于 東

(1.哈爾濱工業大學機電工程學院 哈爾濱，150001) (2.哈爾濱理工大學機械與動力工程學院 哈爾濱，150080) (3.株洲時代新材料科技股份有限公司 株洲，412000)

重卡駕駛室半主動懸置控制方法*

黃山云1, 陳 彬2， 涂奉臣3， 陳照波1， 于 東1

(1.哈爾濱工業大學機電工程學院 哈爾濱，150001) (2.哈爾濱理工大學機械與動力工程學院 哈爾濱，150080) (3.株洲時代新材料科技股份有限公司 株洲，412000)

為了抑制在路面激勵下某型重卡駕駛室的振動加速度響應，研究基于磁流變阻尼器駕駛室半主動懸置系統的控制方法。建立了重卡駕駛室半主動懸置集中質量動力學模型，分別采用比例積分微分(proportion integration differentiation,簡稱PID)控制理論和模糊最優控制理論設計控制器，并利用磁流變阻尼器動力特性實驗數據對模糊最優控制器的參數進行優化。以駕駛室質心垂直、側傾及俯仰3個方向加速度為控制目標，利用ADAMS/Simulink聯合仿真方法，對比分析PID控制和模糊最優兩種控制策略與被動狀態下重卡駕駛室懸置振動控制效果。針對實際重卡進行不同速度路面激勵下的振動控制實驗。仿真和實驗結果表明,采用PID和模糊最優控制方法均能有效抑制重卡駕駛室半主動懸置的振動加速度響應，其中模糊最優控制效果總體優于PID控制。

振動控制; 駕駛室懸置; 磁流變阻尼器; PID控制; 模糊最優控制

引 言

隨著電子商務的快速發展，現代物流產業不僅對交貨時效有嚴格的限定，同時對貨運的安全性和連續性有更高需求，這就要求卡車在運行舒適感、可控性和穩定性等方面具備更好的性能。目前，外國高端商業卡車已經廣泛使用含4個安全氣囊的全浮式駕駛室懸置系統和空氣彈簧懸架系統[1-2]。國內外對全浮式懸置系統的研究主要集中在對駕駛室懸置系統結構參數進行匹配以降低駕駛室內振動[3-4]，對復雜路況的適應能力有限。磁流變阻尼器是一種阻尼力在很大范圍內可控且響應速度快的智能半主動元件[5]，它能在很短的時間內使懸置系統達到最優的結構參數，以適應不同的路面激勵。

筆者以某重型卡車駕駛室懸置為研究對象，建立其6自由度動力學模型，并基于最優控制理論以及磁流變阻尼器動力實驗數據設計模糊最優控制器，利用ADAMS/Simulink聯合對駕駛室半主動懸置控制系統進行仿真分析。路面實驗驗證了該控制系統的有效性。

1 動力學模型

針對某型重型卡車駕駛室懸架結構進行簡化，圖1為卡車駕駛室的簡化集中質量模型示意圖。假定底盤為具有3自由度無質量的平臺，駕駛室簡化為具有集中質量和兩個方向轉動慣量的質量塊。駕駛室通過4個由彈簧和磁流變阻尼器組成的復合隔振單元連接。

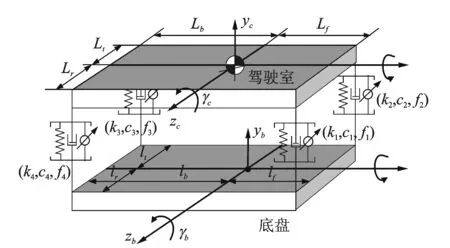
圖1 駕駛室半主動懸置系統示意圖Fig.1 The diagram of the semi-active cab mounting system

圖1中x為行車方向，y為重力反方向，z為側向。根據駕駛室結構特點，假定駕駛室有3個自由度，分別為y方向移動和沿x軸、z軸方向旋轉。圖1中：k1，k2，c1和c2為前懸置減震器剛度和阻尼系數；k3，k4，c3，c4為后懸置減震器剛度和阻尼系數。底盤同樣具備3個自由度，分別為y方向移動和沿x軸、z軸方向旋轉。

令底盤位姿為Xb=[ybαbγb]T；駕駛室位姿為Xc=[ycαcγc]T。根據駕駛室懸置的特點和幾何關系，得到XB=HbXb,XC=HcXc, 其中，Hb和Hc為位移轉換矩陣。

忽略磁流變阻尼器運動部件的質量，根據牛頓力平衡原理推導出駕駛室懸置系統的動力學方程

(1)

其中：Mc和K分別為駕駛室質量、轉動慣量矩陣和隔振單元組成的剛度矩陣，Mc=diag(m,Ixx,Izz),K=diag(k1,k2,k3,k4)；C為隔振單元中的黏性阻尼部分ci組成的阻尼矩陣，C=diag(c1,c2,c3,c4)；U為隔振單元中磁流變阻尼器產生的阻尼力fi組成的控制力向量，U=[f1,f2,f3,f4]T。

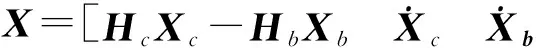
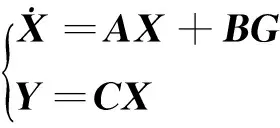
(2)

其中：A為系統矩陣；B為輸入矩陣；G為輸入變量；C為測試矩陣。

2 控制系統設計

基于磁流變阻尼器的駕駛室懸置振動控制的基本原理是通過控制改變懸置系統的阻尼，改變懸置在共振區及高頻區的振動傳遞特性，實現駕駛室懸置在共振區抑制振動、在高頻區隔離振動的目的[6]。

2.1PID控制器

駕駛室半主動懸置系統PID控制器原理框圖如圖2所示。

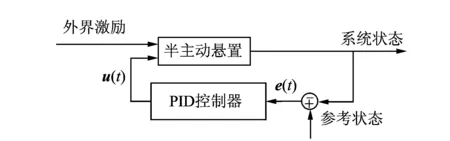
圖2 駕駛室半主動懸置PID控制框圖Fig.2 Block diagrams of PID controller for semi-active cab mounting system

PID控制器的控制規律可以表示為

(3)

其中：Kp為比例系數；Ki為積分系數；Kd為微分系數。

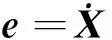
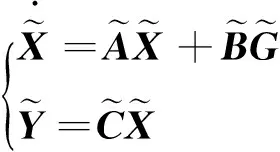
(4)

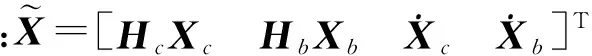
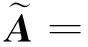
通過控制Kp，Kp和Kp即可改變系統的響應特性。假定系統階躍輸入，以駕駛室質心3個方向速度加權平均值作為優化指標，利用單純形法優化[7-8]即可得到最優的PID控制參數。

2.2 模糊最優控制器

基于建立的駕駛室懸置動力學模型，考慮到建立磁流變阻尼器精確控制模型比較困難，筆者采用模糊最優控制器實現對駕駛室懸置的振動控制。控制器結構原理如圖3所示。模糊最優控制器由兩部分組成：a.基于駕駛室懸置動力學模型設計的最優控制器；b.基于磁流變阻尼器動力特性實驗數據的模糊控制器。經最優控制算法計算其最優控制力，輸入給模糊控制器，模糊控制器根據最優控制力以及阻尼器狀態量dx計算其控制電流，并輸出給各個阻尼器，從而改變可控阻尼器的輸出阻尼力。

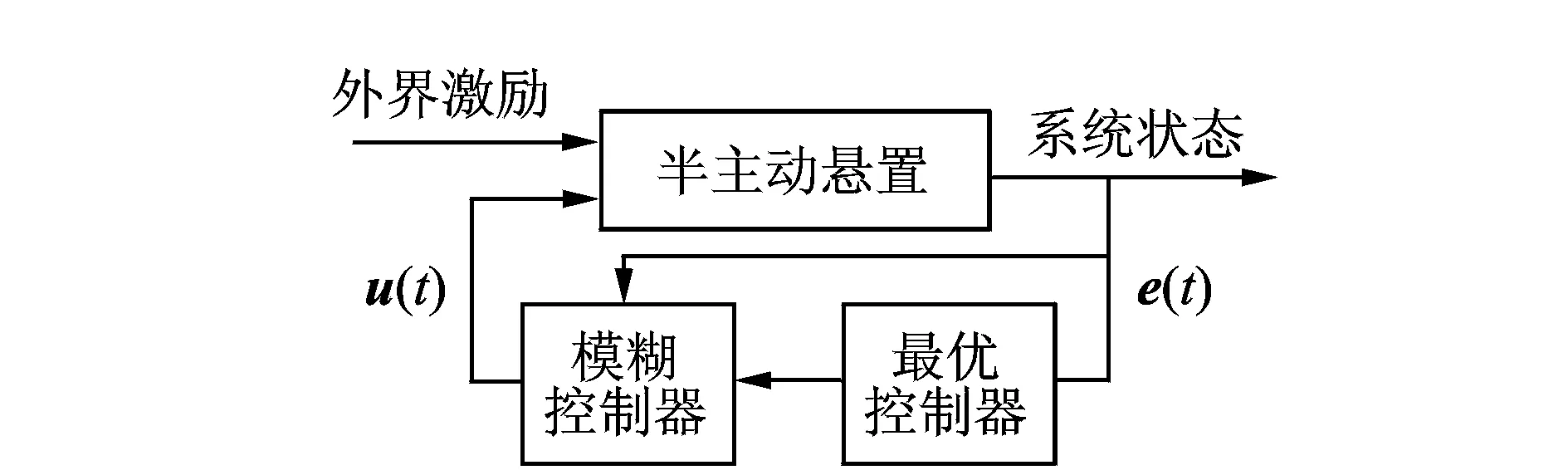
圖3 駕駛室半主動懸置模糊最優控制框圖Fig.3 Block diagrams of fuzzy optimal controller controller for semi-active cab mounting system

2．2．1 最優控制器

系統動力學方程如式(2)所示，以駕駛室垂直方向、俯仰角和側傾角的速度加權平方和最小作為優化目標，即有

(5)

其中：狀態加權矩陣Q為非負正定對稱陣，控制加權矩陣R正定對稱陣[9]。

通過構造哈密頓函數以及變分極值條件可知，存在反饋控制律使得優化目標極小。

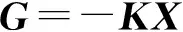
(6)

其中：K為狀態反饋系數，且K滿足

(7)

S滿足Riccati代數方程。

(8)

2．2．2 阻尼器模糊控制器設計

由于磁流變阻尼器的強非線性特性，建立其準確控制模型比較困難[10]。描述非線性特性是智能算法的強項，因此有學者提出利用神經網絡[11]和模糊理論[12]設計磁流變阻尼器控制器。相比于神經網絡控制器，模糊控制器具有算法簡便，計算延遲小等優點。筆者利用模糊控制理論，基于磁流變阻尼器的動力特性實驗數據，設計磁流變阻尼器控制器。將E，Ec和U分別用NB，NM，NS，ZE，PS，PM和PD語言變量表示，建立一組模糊控制規則[12]

Rn: ifeisAnandecisBn, then isCn,n=1,2,3, …

其中：An為e的模糊集合；Bn為ec的模糊集合；Cn為u的模糊集合。

根據磁流變阻尼器力學特性曲線如圖3所示，可將磁流變阻尼器的相對速度、輸入電流和阻尼力分別模糊化，并根據圖4建立阻尼器輸出力與電流之間關系的模糊規則如表1所示。

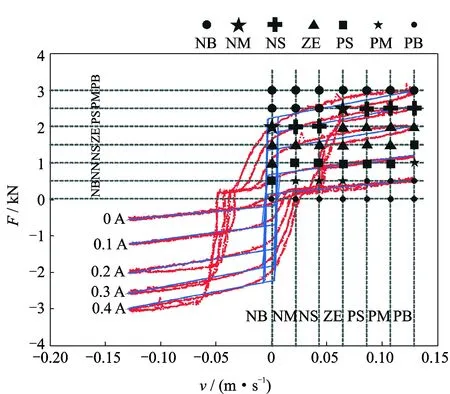
圖4 磁流變阻尼器速度-力曲線Fig.4 The velocity-force curve of magnetorheological damper

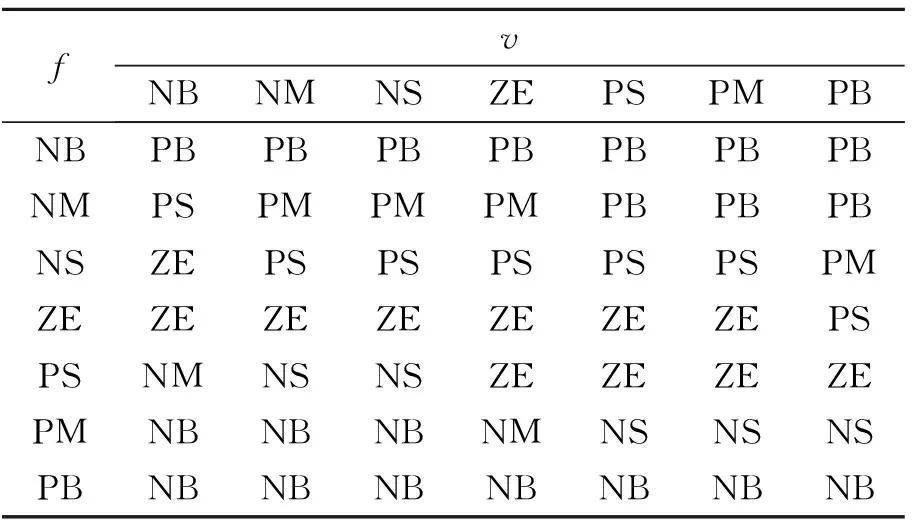
fvNBNMNSZEPSPMPBNBPBPBPBPBPBPBPBNMPSPMPMPMPBPBPBNSZEPSPSPSPSPSPMZEZEZEZEZEZEZEPSPSNMNSNSZEZEZEZEPMNBNBNBNMNSNSNSPBNBNBNBNBNBNBNB

筆者采用重心法進行解模糊，該方法耗時短, 可用足夠小的采樣時間提供所需的精度[13]。重心法表達式[14]為

(9)

其中：y*為整體面積中心所對應的坐標；μ為模糊隸屬度函數；y∈Y；Y為連續論域。

3 仿真計算

為了驗證模糊最優控制器在駕駛室半主動懸置系統中的控制效果，筆者基于某型重型卡車的駕駛室懸置系統的結構參數，利用ADAMS建立駕駛室懸架的多體動力學模型，如圖5所示。駕駛室懸置的主要參數如表2所示。

圖5 駕駛室半主動懸置ADAMS模型Fig.5 ADAMS model of semi-active cab mounting system

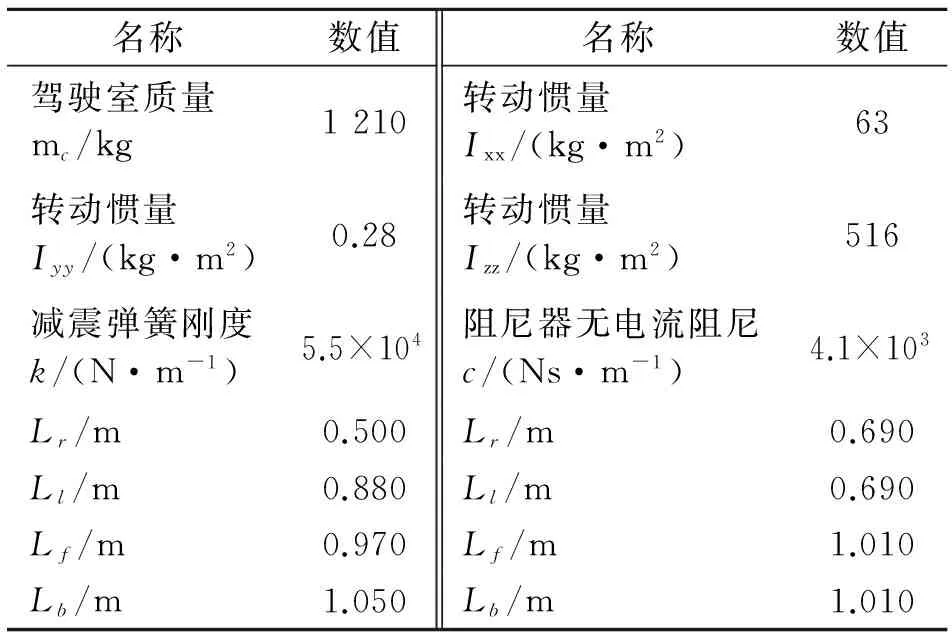
名稱數值名稱數值駕駛室質量mc/kg1210轉動慣量Ixx/(kg·m2)63轉動慣量Iyy/(kg·m2)0.28轉動慣量Izz/(kg·m2)516減震彈簧剛度k/(N·m-1)5.5×104阻尼器無電流阻尼c/(Ns·m-1)4.1×103Lr/m0.500Lr/m0.690Ll/m0.880Ll/m0.690Lf/m0.970Lf/m1.010Lb/m1.050Lb/m1.010

在ADAMS模型中，磁流變阻尼器被簡化為外部控制的阻尼力約束，同時在Simulink中建立對應的函數模型，用以模擬真實的磁流變阻尼器。同時在Simulink搭建模糊最優控制器模型，并與ADAMS搭建的駕駛室懸架模型進行聯合仿真控制。

假定卡車右前方車輪以一定速度通過一凸起路面，即底盤在yb,αb,γb方向同時受到(角)位移脈沖激勵。假定其幅值分別為10 mm,1.24°和0.64°，持續時間為1 s。

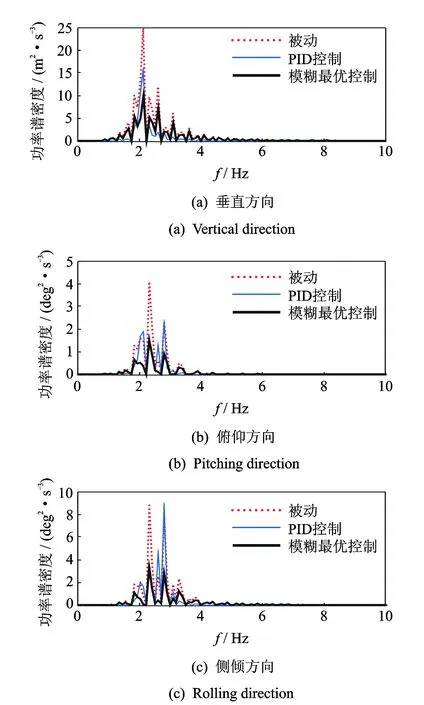
圖6 駕駛室質心加速度響應功率譜密度結果Fig.6 Accelerate power spectrum density result of cab

不同控制方式下駕駛室加速度響應結果如圖6所示。由圖6可知，相比被動方式采用PID控制和模糊最優控制方式均能降低駕駛室懸置的加速度響應值，且在共振區(2～3 Hz處)減振效果明顯。相比于PID控制方式，模糊最優控制器在共振峰抑制方面更具優勢。其原因在于PID控制器控制參數較少，可利用的系統狀態量也少，且效果依賴參數優化程度。

4 實 驗

為了進一步驗證駕駛室半主動懸置控制系統的有效性，筆者針對某型重卡駕駛室懸置進行路面實驗。實驗裝置如圖7所示。

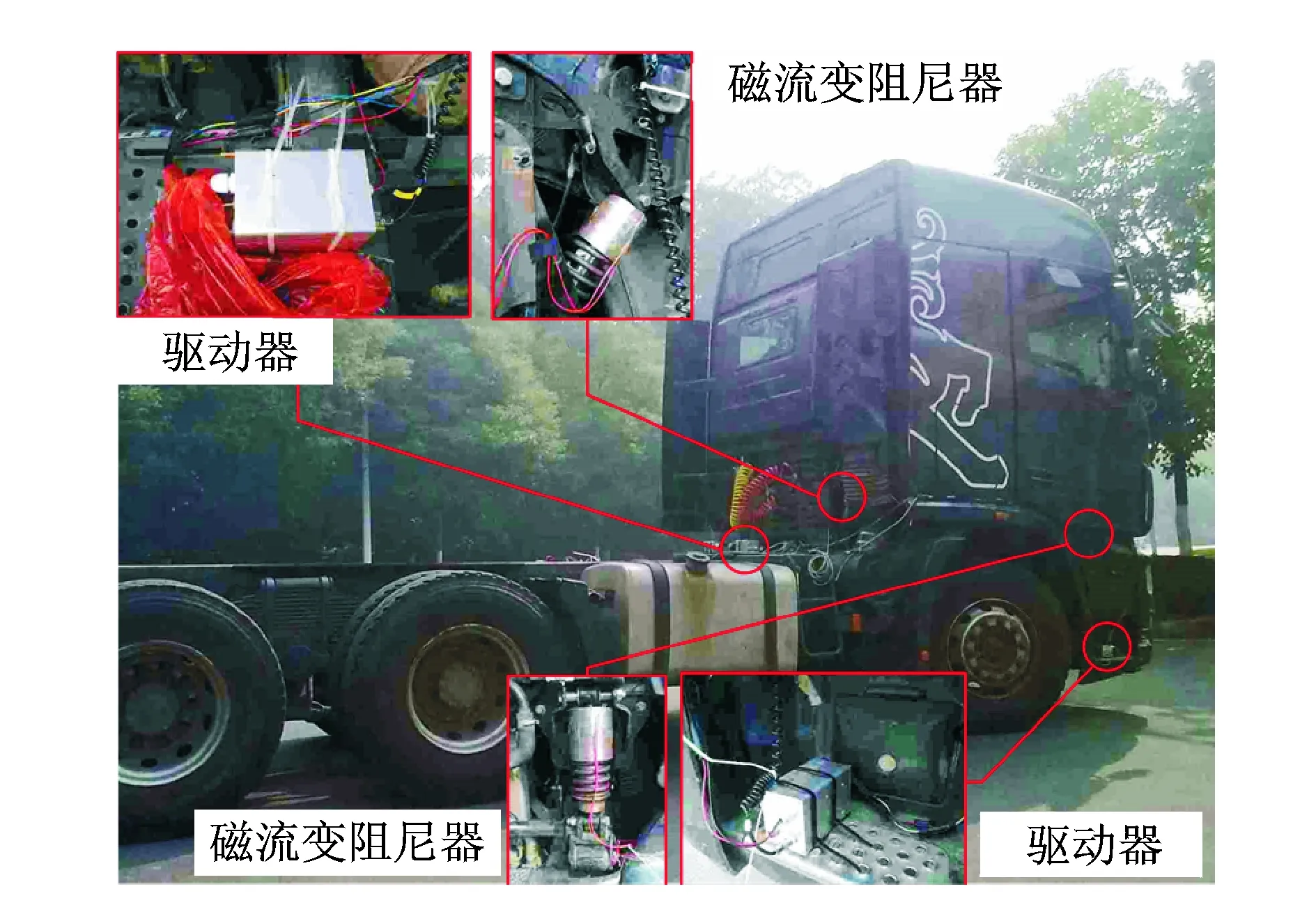
圖7 駕駛室半主動懸置控制實驗裝置Fig.7 Experiment facility of semi-active cab mounting system

分別將車速設為為40，50，60，70和80 km/h,測得不同控制方法下駕駛室座椅處沿垂直(y)、俯仰(x)和側傾(z)方向的加速度響應。圖8為時速50 km下座椅3個方向的加速度功率譜圖。

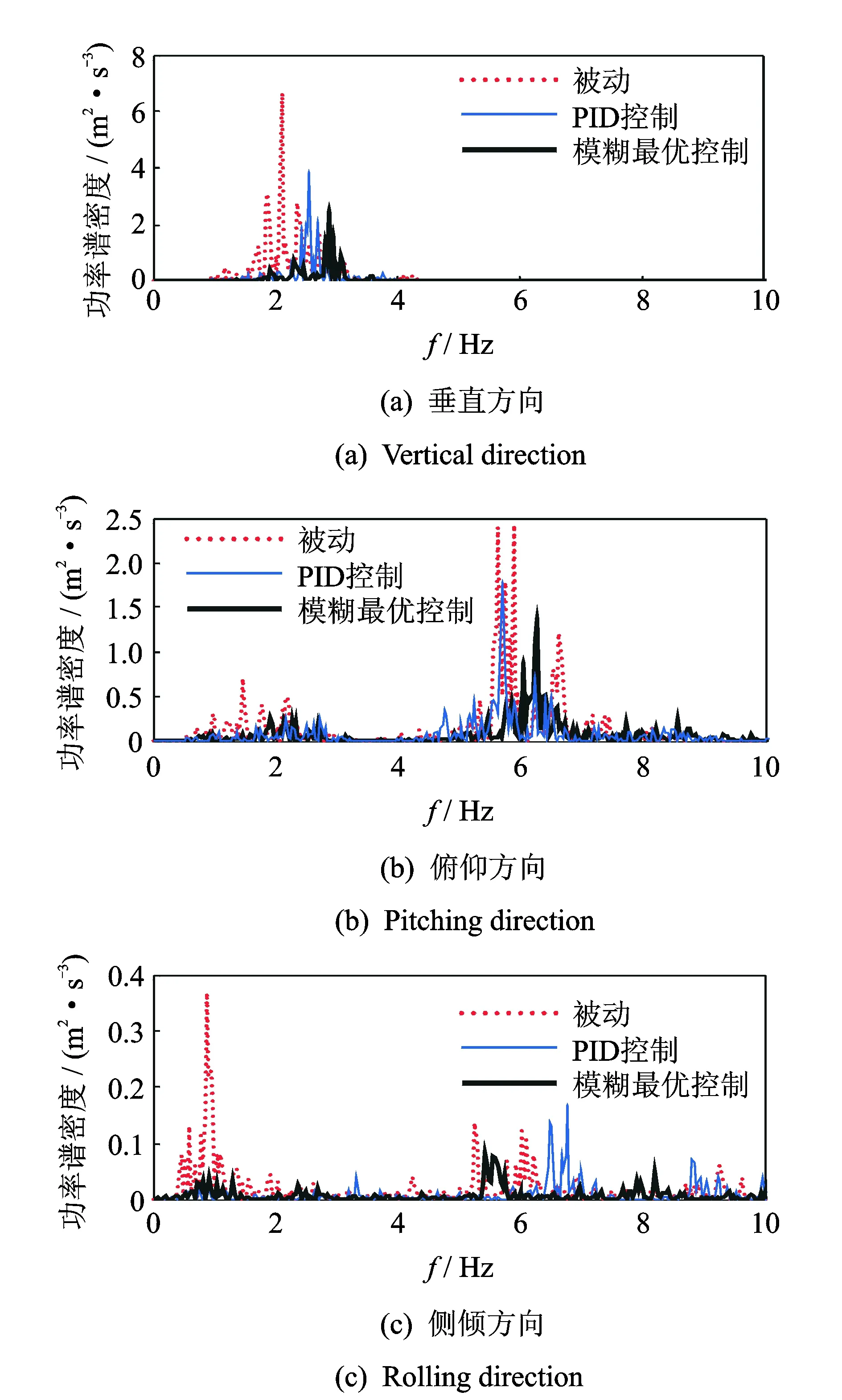
圖8 時速為50 km時座椅加速度功率譜 Fig.8 Accelerate power spectrum result of cab at 50 km/h

由圖8可知,當汽車行駛速度為50 km/h時， 相比被動方式，PID控制和模糊最優控制方法均能有效抑制座椅在3個方向的加速度，尤其是在共振頻率附近，其中模糊最優控制效果優于PID控制。圖8(c)中高頻處PID控制出現峰值，原因是在PID控制作用下懸架系統等效剛度發生變化，導致共振頻率增加。因高頻處有座椅系統衰減，故對振動控制效果影響較小。表3～5分別為不同速度下座椅垂直、俯仰和側傾方向的加速度均方根值。

從表3可以看出，相比于被動，模糊最優控制方法和PID控制方法均能有效降低座椅垂直方向加速度均方根值，同時模糊最優控制整體效果優于PID控制效果。采用PID方法,座椅垂直方向的加速度均方根值在50 km/h處比無控制時減小28.9%，采用模糊控制則減小40.4%。表4和表5結果顯示，在座椅俯仰和側傾方向，模糊最優控制方法和PID控制方法均能有效降低座椅垂直方向的加速度均方根值。以加速度均方根值為振動控制效果評價標準，在車速小于70 km/h時相比于PID控制，模糊最優控制效果略優，但在速度大于70 km/h時，PID控制略優于模糊最優控制效果，這種情況同樣出現在表3和表5中。結合實驗現場情況，筆者認為隨著車速的增加，道路對車輛的激勵頻率和動載荷均發生變化，此時實際駕駛室并不能簡單地利用剛體模型描述。相比于PID控制，模糊最優控制對模型精度更為敏感，當實際模型與理論模型存在一定差異時，將導致PID控制效果好于模糊最優控制效果。

表3 不同速度下座椅垂直方向加速度均方根值

Tab.3 The accelerate RMS of seat in vertical direction under different speed

v/(km·h-1)被動PID模糊最優401.14850.84240.8480501.84371.31111.0994601.26681.57391.0337701.92991.74401.1860802.11081.27831.6775

表4 不同速度下座椅俯仰方向加速度均方根值

Tab.4 The accelerate RMS of seat in pitching direction under different speed

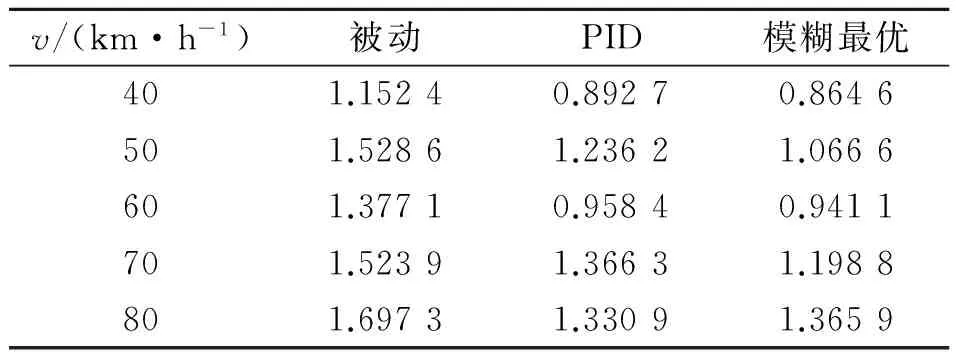
v/(km·h-1)被動PID模糊最優401.15240.89270.8646501.52861.23621.0666601.37710.95840.9411701.52391.36631.1988801.69731.33091.3659

表5 不同速度下座椅側傾方向加速度均方根值

Tab.5 The accelerate RMS of seat in rolling direction under different speed

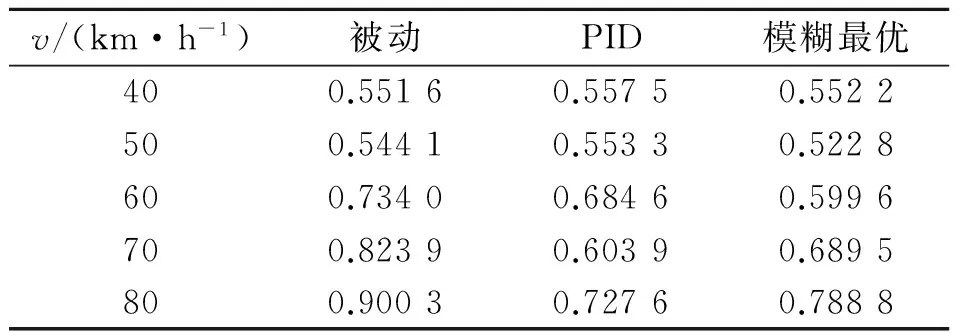
v/(km·h-1)被動PID模糊最優400.55160.55750.5522500.54410.55330.5228600.73400.68460.5996700.82390.60390.6895800.90030.72760.7888

5 結束語

采用模糊最優控制策略，在駕駛室半主動懸架集中質量動力學模型的基礎上構建半主動懸架系統模糊最優控制器，并利用磁流變阻尼器動力特性實驗數據對模糊最優控制器參數進行優化。利用ADAMS/Simulink聯合仿真研究PID控制器和模糊最優控制器。結果表明：采用模糊最優控制器和PID控制器的半主動懸置能顯著抑制駕駛室質心處垂直、側傾及俯仰3個方向的加速度值。相比于PID控制器，模糊最優控制器在共振頻率附近的抑制效果更好。重型卡車路面實驗也驗證了仿真結果的正確性，同時發現當車速增加到一定值(70 km/h)以上時，對模型精度依賴較低的PID控制反而能獲得比模糊最優控制更好的控制效果。

[1] Wang Dongfeng, Hao He, Zhang Bin, et al. Simulation and test on virtual prototype of heavy-duty truck with full-floating cab and air suspension [C]∥ International Conference on Computer Design and Appliations (lCCDA 2010).[S.l.]: IEEE, 2010: 209-213.

[2] 張偉.商用車駕駛室懸置系統動力學特性研究[D]. 廣州：華南理工大學, 2012.

[3] 雷飛,楊紅波. 基于模糊控制的商用車駕駛室懸置有限帶寬主動控制系統研究[J]. 工程設計學報, 2014(1): 32-37.

Lei Fei, Yang Hongbo. Research on a bandwidth-limited active control system for commercial vehicle cab suspension based on the fuzzy theory [J]. Chinese Journal of Engineering Design, 2014(1): 32-37.(in Chinese)

[4] 朱祝英,馬力,張宇龍,等. 考慮整車的剛柔多體全浮式駕駛室懸置系統參數優化設計[J]. 噪聲與振動控制, 2009(4): 91-93.

Zhu Zhuying, Ma Li, Zhang Yulong, et al. Parameterized optimal design of fully-float cab suspension system of commercial vehicles based on the theory of rigid-flexible dynamics[J]. Noise and Vibration Control,2009(4): 91-93.(in Chinese)

[5] 周云,譚平. 磁流變阻尼控制理論與技術[M]. 北京: 科學出版社, 2007: 33-35.

[6] Hiemenz G J, Hu W, Wereley N M. Semi-active magnetorheological helicopter crew seat suspension for vibration isolation[J]. Journal of Aircraft, 2008, 45(3): 945-953.

[7] 劉曉謙,王勇,穆順勇. 基于單純形法的PID控制器參數優化設計[J]. 計算機仿真, 2004(11): 191-193.

Liu Xiaoqian, Wang Yong, Mu Shunyong. Design of optimal parameters for PID controller based on simplex search [J]. Computer Simulation, 2004(11): 191-193. (in Chinese)

[8] 張磊. 基于單純形法的PID控制器的最優設計[J]. 信息與控制, 2004,33(3): 376-379.

Zhang Lei. Method based optimal design of PID controller [J]. Information and Control, 2004, 33(3): 376-379. (in Chinese)

[9] Dorf R C,H bishop R. 現代控制系統[M]. 北京: 電子工業出版社, 2009: 790-791.

[10]Phu D X, Shah K, Choi S. Design of a new adaptive fuzzy controller [J]. Smart Material Structural,2014, 23:1-18.

[11]廖英英, 劉永強, 楊紹普，等. 磁流變阻尼器逆向模型的建模、優化與仿真[J]. 振動、測試與診斷, 2013,33(4):701-705.

Liao Yingying, Liu Yongqiang, Yang Shaopu,et al. Modeling optimization and simulation of a magneto- rheological damper[J].Journal of Vibration, Measurement & Diagnosis, 2013,33(4):701-705. (in Chinese)

[12]李忠獻,徐龍河. 新型磁流變阻尼器及半主動控制設計理論[M]. 北京: 科學出版社, 2012: 271-273.

[13]涂奉臣,陳照波,劉望中,等. 新型半主動整星隔振平臺及其模糊最優控制研究[J]. 振動工程學報, 2010(2): 133-139.

Tu Fengchen, Chen Zhaobo, Liu Wangzhong, et al. A new type semi-active whole-spacecraft isolation platform [J]. Journal of Vibration Engineering, 2010(2): 133-139. (in Chinese)

[14]董早鵬. 無人艇運動模糊控制技術研究 [D]. 哈爾濱: 哈爾濱工程大學, 2013.

10.16450/j.cnki.issn.1004-6801.2016.01.028

??基金資助項目(10972065；11372083)

2014-10-12；修回日期：2015-01-29

U461.1; TH113.1

黃山云，男，1986年8月生，博士生。主要研究方向為基于磁流變的振動半主動控制。曾發表《Mechanical-delay dynamic model of magnetorheological Damper》(《Journal of Donghua University:English Edition》2014,Vol.31,No.4)等論文。

E-mail：shanyunh@foxmail.com