單室雙推力發動機裝藥的瞬態結構完整性分析*

龔建良,樊學忠,李宏巖,王 中

(西安近代化學研究所,西安 710065)

單室雙推力發動機裝藥的瞬態結構完整性分析*

龔建良,樊學忠,李宏巖,王 中

(西安近代化學研究所,西安 710065)

針對單室雙推力發動機裝藥在低溫點火工況下結構完整性,為了求解損傷的熱粘彈性有限元模型,采用增量有限元方法,獲取了裝藥內部的應力應變場。研究表明,在固化降溫時,人工脫粘層對裝藥頭部與尾部起到應力釋放的作用,避免了裝藥與絕熱層界面的破壞;同時,裝藥內部Mises應力值較大的部位是過渡段翼尖處與圓柱段表面。在點火時刻,裝藥環向應變的值較大部位是圓柱段表面。最后,采用文中方法,可應用于指導發動機裝藥設計與安全評估。

固體火箭發動機;粘彈性;本構關系;結構完整性;應變軟化

0 引言

針對戰術防空導彈,由于導彈空氣阻力與速度的平方成正比,為了提高導彈射程,采用的動力類型是雙推力形式[1]。雙推力發動機類型主要分雙脈沖、澆鑄型單室雙推力、自由裝填型單室雙推力、裝填與澆鑄混合型單室雙推力等,澆鑄型單室雙推力的裝藥對殼體具有熱防護功能,絕熱層可以鋪設的較薄,可以通過調整燃面或燃速,改變發動機的推力比,推力比調節范圍大,因此,澆鑄型單室雙推力發動機在戰術防空導彈中被廣泛采用。

單室雙推力發動機裝藥設計主要有藥型設計、內彈道計算與結構完整性分析等,藥型設計作為發動機設計的核心部分,為了提高裝藥的裝填比,裝藥的M數(發動機外徑/裝藥內徑)一般較高,長徑比大(達到10)[2]。在點火過程中,結構完整性安全余度較低,降低了發動機工作可靠度與安全度。為了充分發揮推進劑能量水平,發動機設計壓力一般較高,高溫下超過20 MPa,要求結構完整性具有高可靠度。澆鑄型單室雙推力是采用燃速或燃面調整推力比,一般內部燃面復雜,具有三維特征;同時,在單室雙推力發動機內部,一般具有應力釋放結構(如人工脫粘層或襯墊)及發動機內部存在復雜的多界面接觸,難以采用經典的平面應變或平面應力模型評估裝藥在溫變或點火過程的結構完整性。由于熱粘彈性理論、損傷與斷裂力學日趨完善,采用熱粘彈性有限元方法,可以較為精確的評估發動機裝藥結構完整性,為發動機裝藥安全評估提供一種手段。

針對固體火箭發動機裝藥結構完整性,國內外進行了廣泛研究,Park與Schapery基于有限元軟件ABAQUS,采用粘彈性本構模型,編寫用戶子程序UMAT,對復合固體推進劑試件進行結構計算,同時采用雙軸拉伸試驗的數據驗證仿真結果,二者吻合較好[3-4]。同時,Hinterhoelzl與Schapery,在文獻中[5]給出了用戶子程序的詳細數值處理過程。Chen與Leu針對含應力釋放槽的裝藥,基于MSC/NASTRAN有限元軟件,采用結構化網格,通過仿真確定了裝藥的最優幾何尺寸[6]。Chyuan基于熱粘彈性模型,采用縮減積分單元克服了推進劑的不可壓縮性,研究了多種點火壓力工況的瞬態結構完整性,通過與靜態分析相比較,表明了瞬態結果的預估精度更高[7]。同時,Chyuan分析了不同泊松比對裝藥內部應力場分布的影響[8]。強洪夫等基于Swanson大變形粘彈性本構模型,針對Finne裝藥模型,分析了體積模量對計算結果的影響[9]。劉中兵分析了不同軸向過載條件下的藥柱結構完整性[10]。李磊針對傘盤型裝藥,基于MSC.Patran/Marc軟件,對裝藥結構幾何尺寸進行了優化分析,研究了藥柱Von Mises應變與體積裝填分數隨幾何參數的變化規律,獲取了裝藥關鍵尺寸[11]。李東與孟洪磊基于ABAQUS軟件,發展了一種新型損傷函數,通過二次開發實現了裝藥結構完整性分析,并考慮裝藥內部裂紋的影響[12-13]。鄧斌等采用經典損傷理論,建立損傷本構模型,進行了結構完整性分析[14]。

可知,國內外已經分析了材料屬性、幾何結構、外部載荷對藥柱結構完整性影響,然而單室雙推力發動機裝藥在高壓下的結構完整性缺乏深入與詳細研究。由于推進劑是一種粘彈性材料,存在玻璃化溫度轉變特點,低溫誘發藥柱內孔收縮,增加了發動機在低溫點火的危險性,因此,文中針對單室雙推力發動機裝藥,分析了在低溫高壓下裝藥的瞬態結構完整性。

1 本構模型

復合固體推進劑具有力學性能良好,能量水平高,燃速調整范圍大,是單室雙推力發動機主要的推進劑。然而復合固體推進劑是一種粒子增強體復合材料,粒子體積分數高達80%,比表面積大,導致其力學行為復雜,如粘彈性、大應變、Mullin效應與體積膨脹等。采用合適的本構模型描述復合固體推進劑的力學行為,才能保證裝藥結構完整性的預估精度。無損傷的復合固體推進劑,可以采用線粘彈性或彈性本構模型描述其力學行為,但是復合固體推進劑在固化成型、運輸、貯存與使用條件下,存在各種力載荷與溫度載荷,容易誘發裝藥內部各種形式的損傷,如粘合劑微小裂紋、粘合劑與AP粒子界面脫粘、AP粒子破碎等,因此需要采用損傷的粘彈性本構模型才能正確描述復合固體推進劑的力學行為。

粘彈性復合固體推進劑的力學相應由偏響應與體響應組成,應力應變可依據式(1)與式(2)分解。以Von Mises應變為準則,建立軟化函數描述力學響應的損傷程度,如式(3)與式(4)。

(1)

(2)

(3)

(4)

(5)

(6)

式中:G(t)為剪切松弛模量;K(t)為體積松弛模量;α0是熱膨脹系數;εmises是Von Mises應變,由3個主應變ε1、ε2、ε3確定,依據式(7):

(7)

縮減時間ξ、ξ′由時溫轉化因子αT確定,依據式(8):

(8)

各向同性的損傷函數,以拉伸曲線的脫濕點為界限,在脫濕點之前是線粘彈性,在脫濕點之后是非線性粘彈性,損傷函數以應變軟化函數的形式給出為:

(9)

式中:參數α1、α2由單向拉伸曲線擬合確定,依據典型配方HTPB復合固體推進劑的單項拉伸數據確定了α1=1.54、α2=1.72;εdebond是單向拉伸曲線的脫濕點應變,εdebond=10.1%。

溫度的影響依據時溫轉化方程W.L.F.,轉化為時間的影響,如式(10):

(10)

式中:C1、C2是材料參數;T0是參考溫度。

2 應力更新方程與一致切線剛度矩陣

采用損傷的粘彈性本構模型描述復合固體推進劑的力學行為,粘彈性材料的力學響應與加載歷史、時間、溫度是相關的,為了進行有限元的數值計算,采用增量法求解有限元方程。基于商業有限元軟件,通過二次開發,實現粘彈性本構模型,需要提供應力更新方程與一致切線剛度矩陣[5]。

(11)

(12)

(14)

3 結構完整性計算與分析

3.1 計算模型與網格劃分

針對某單室雙推力發動機的結構特點,建立了由殼體、絕熱層、藥柱、人工脫粘層組成的幾何模型,考慮幾何模型與載荷的對稱性,取1/16建立計算模型,并做如下假設:

1)殼體、絕熱層與藥柱界面是完全粘接;

2)人工脫粘層與藥柱界面是完全粘接,人工脫粘層與絕熱層界面是法向自由,切向具有摩擦力;

3)絕熱層與藥柱是粘彈性材料,泊松比取定值;

4)不考慮發動機平衡壓力對內表面變形的影響,以芯模的初始表面建立計算模型。

結構化網格具有網格數量少、計算速度快的優點,采用六面體網格劃分計算模型,結果如圖1,網格數是16 725個;局部網格放大圖,如圖2。

圖1 1/16裝藥模型的網格劃分

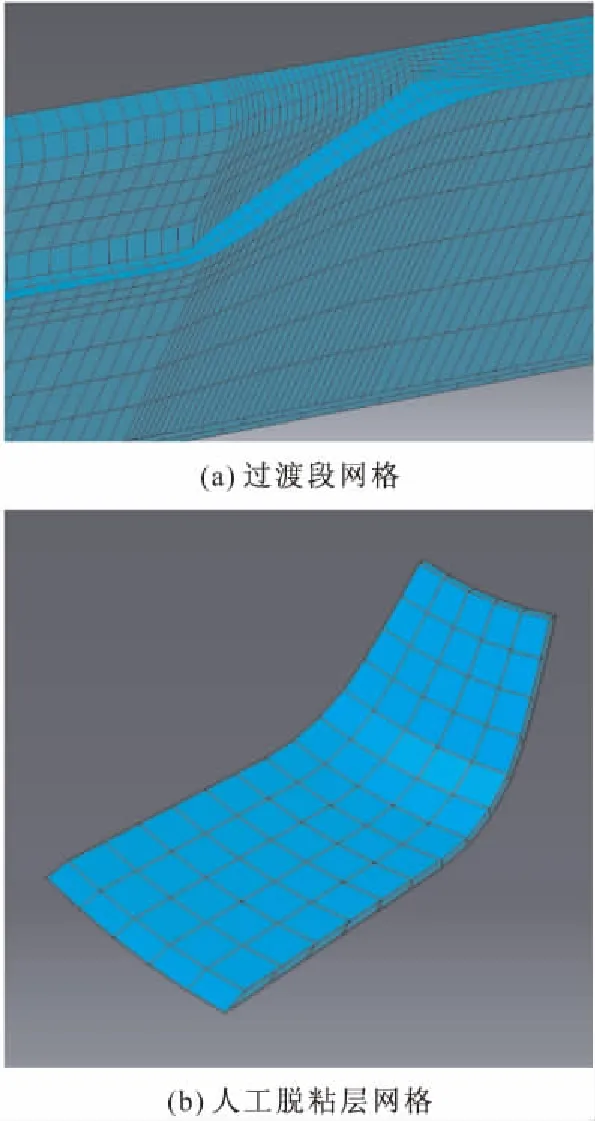
圖2 局部網格放大

3.2 邊界條件與材料屬性

針對單室雙推力發動機在導彈的安裝位置,建立相類似的約束條件。在殼體前裙與后裙表面約束所有自由度;在對稱面,采用對稱條件。推進劑固化的零應力溫度是68 ℃,在烘箱內存放24 h后,溫度達到-40 ℃;迅速轉移發動機,并在試車臺安裝與點火,0.3 s內建立平衡壓力18.5 MPa。

發動機受溫度與內壓的聯合作用,文中的粘彈性模型對溫度與應力的求解采用解耦處理,忽略應力應變對溫度場的影響,根據已知的溫度場展開應力應變場的數值計算。材料的具體參數,如表1;推進劑的剪切松弛模量如式(15);包覆層的剪切松弛模量如式(16);溫度的影響,包覆層與推進劑采用相同的W.L.F.方程,如式(17)。

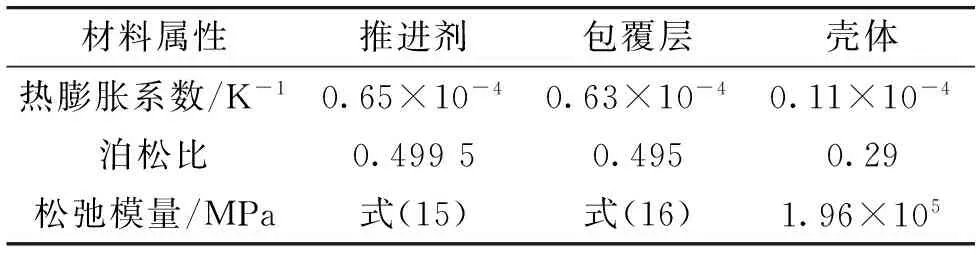
表1 發動機內各材料的屬性

(15)

(16)

(17)

3.3 計算結果與分析

采用應變損傷的軟化函數,綜合描述了推進劑內部的損傷狀態,結合粘彈性有限元算法,計算了某型號單室雙推力發動機裝藥結構完整性,獲取了裝藥內部的應力應變場分布。圖3給出了在固化降溫過程中,裝藥內部Mises應力場,可知在固化降溫時,圓柱段表面、過渡段尖部是危險部位,應力不能超過推進劑的拉伸強度。裝藥設計的內孔尺寸過小,內表面容易發生表面裂紋,在點火載荷作用極易發生裂紋擴展,并沿裝藥內部撕裂,增加異常燃面,提前暴露絕熱層,增加燒蝕量,并最終導致殼體表面提前暴露在高溫燃氣中,出現發動機安全事故,因此裝藥的內孔尺寸需要一定的安全裕度。

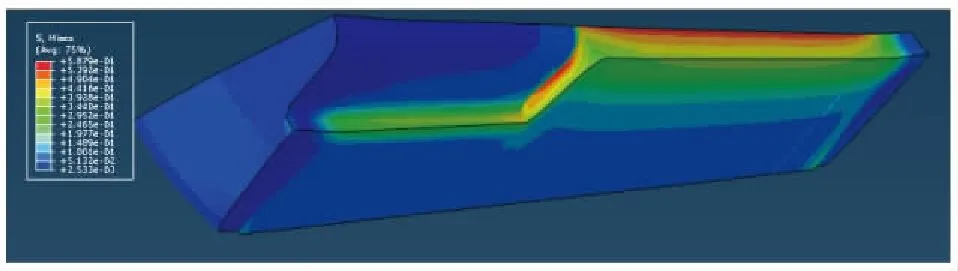
圖3 保溫至-40 ℃后藥柱的Mises應力分布

人工脫粘層作為裝藥設計的一個重要組成部分,在固化降溫過程,往往容易發生界面脫粘。圖4給出了前/后人工脫粘層與絕熱層界面在固化降溫后的界面狀態。可知由于藥柱的收縮,導致人工脫粘層與絕熱層界面處于分離狀態,前人工脫粘層與絕熱層界面位移最大是2.57 mm,后人工脫粘層與絕熱層界面位移最大是1.94 mm。為了防止點火過程火焰在人工脫粘層內竄火,需要在點火之前采用阻燃材料填充人工脫粘層與絕熱層的分離間隙。

在點火時刻,由圖5可知應力應變都比在固化降溫時增大,裝藥危險部位也是在圓柱段、翼槽尖部,發動機在固化降溫后,采用內窺鏡檢查裝藥表面,安全裕度留足,保證點火安全性與工作可靠性。

推進劑的內孔表面裂紋是最主要的一種失效模式。由于在溫變與內壓聯合作用下,裝藥的內孔表面產生環向拉伸,環向應變容易導致發動機內部表面產生裂紋。圖6給出了在點火0.3 s時刻,藥柱的環向應變值。可知環向應變是正值,說明在內孔環向受到拉伸作用,且最大值出現在過渡段的星尖處,在翼槽的星尖與圓柱段表面的環向應變都是較大。環向應變的數值沿徑向逐漸降低。

由于內孔表面位移的大小直接影響發動機的初始燃面,從而改變發動機的內彈道特性。圖7給出了在點火0.3 s時刻藥柱的位移。可知由于低溫藥柱收縮與壓力沖擊,藥柱表面受到壓縮作用。位移最大部位是圓柱段,由于圓柱段受到壓縮,藥柱向后移動變形的程度加劇,位移最大值達到7 mm。沿徑向方向,隨半徑增大,位移數值減小。

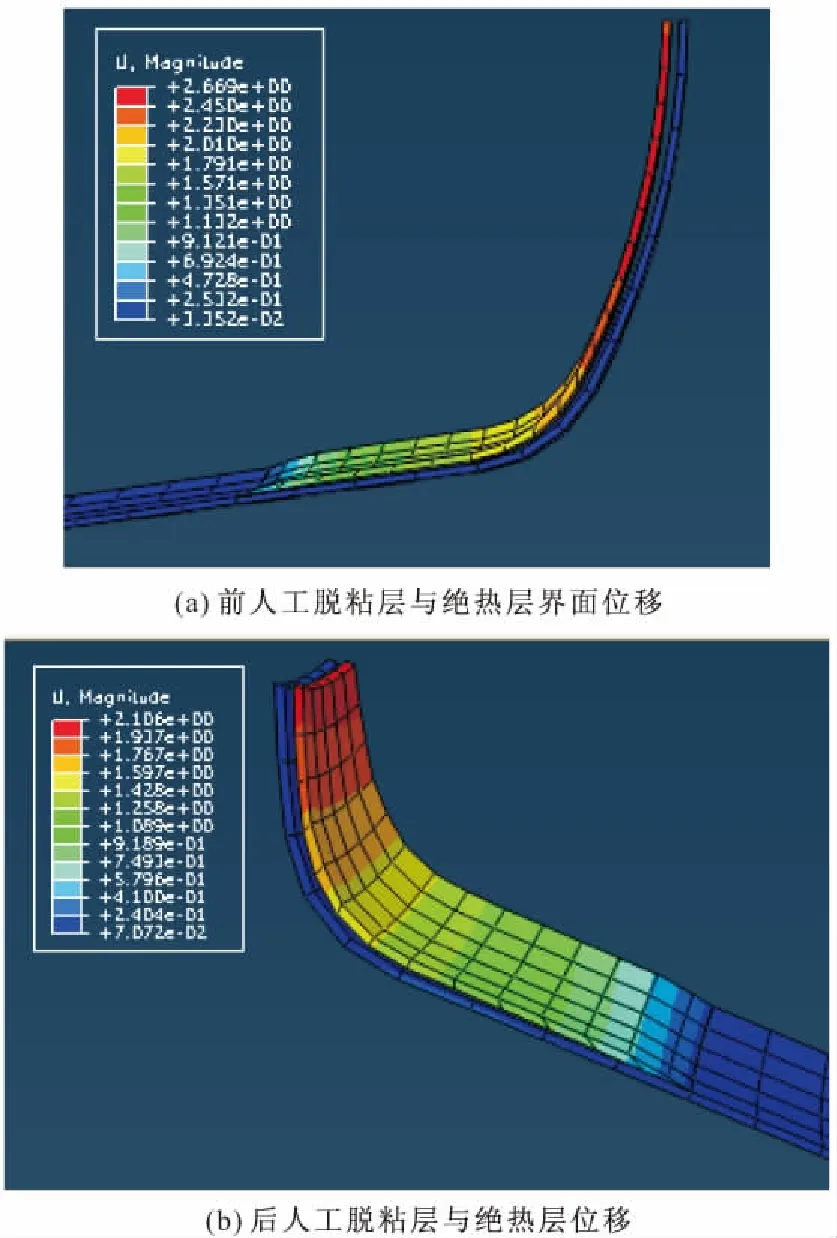
圖4 保溫至-40 ℃后人工脫粘層與絕熱層界面位移

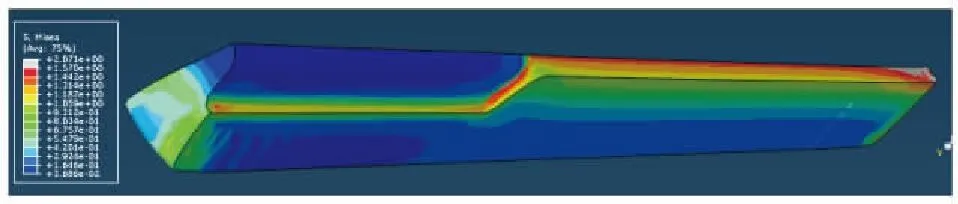
圖5 在點火0.3 s時刻藥柱的Mises應力分布

圖6 在點火0.3 s時刻藥柱的環向應變

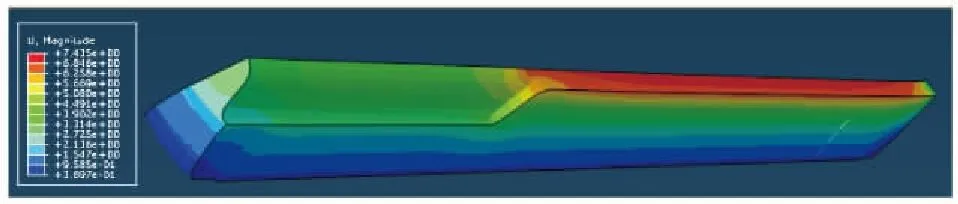
圖7 在點火0.3 s時刻藥柱的位移

最后,針對澆鑄型單室雙推力發動機,在設計與生產過程,保證裝藥具有高裝填比,藥型工藝良好,內彈道曲線特性滿足要求,依據推進劑的強度與延伸率,可以采用文中方法指導裝藥結構設計與校核裝藥安全系數,重點關注裝藥圓柱段內表面、過渡段翼尖處與前后人工脫粘層。

4 結論

采用了一種損傷的熱粘彈性模型,通過二次開發,將其應用于國內某型號單室雙推力發動機裝藥在高壓點火下結構完整性分析,獲取了裝藥內部應力應變場的變化規律。裝藥在固化降溫過程中保證Mises應力值滿足強度要求。在點火時刻,避免裝藥內部發生宏觀裂紋,裝藥環向應變值不能過大。文中的研究方法,為裝藥幾何尺寸的分析提供一種評判方法,可應用于發動機裝藥溫變與點火的安全性評估。

[1] 于劍橋, 文仲輝, 梅躍松, 等. 戰術導彈總體設計 [M]. 北京: 北京航空航天大學出版社, 2010: 138-141.

[2] 王元有. 固體火箭發動機設計 [M]. 北京: 北京理工大學出版社, 1984: 156-171.

[3] PARK S W, SCHAPERY R A. A viscoelastic constitutive model for particulate composites with damage growth [J]. International Journal of Solids and Structures, 1997, 34(8): 931-947.

[4] HA K, SCHAPERY R A. A three-dimensional viscoelastic constitutive model for particulate composites with growing damage and its experimental validation [J]. International Journal of Solids and Structures, 1998, 35(26): 3497-3517.

[5] HINTERHOELZLl R M, SCHAPERY R A. FEM implementation of a three-dimensional viscoelastic constitutive model for particulate composites with damage growth [J]. Mechanics of Time-Dependant Materials, 2004, 8(1): 65-94.

[6] CHEN J T, LEU S Y. Finite element analysis, design and experiment on solid propellant motors with stress reliever [J]. Finite Elements in Analysis and Design, 1998, 29(2): 75-86.

[7] CHYUAN S W. Nonlinear thermoviscoelastic analysis of solid propellant grains subjected to temperature loading [J]. Finite Elements in Analysis and Design, 2002, 38(7): 613-630.

[8] CHYUAN S W. Dynamic analysis of solid propellant grains subjected to pressurization loading [J]. Jounal of Sound and Vibration, 2003, 268(3): 465-483.

[9] 強洪夫, 汪亮. 固體火箭發動機藥柱大變形數值分析 [J]. 宇航學報, 2000, 21(增刊): 77-82.

[10] 劉中兵, 利鳳祥, 李越森, 等. 高過載條件下固體推進劑藥柱結構完整性分析計算 [J]. 固體火箭技術, 2003, 26(6): 12-16.

[11] 李磊. 基于結構完整性分析的固體火箭發動機藥型改進與優化設計 [D]. 長沙: 國防科學技術大學, 2011.

[12] 李東. 固體推進劑藥柱表面裂紋動態力學特性研究 [D]. 南京: 南京理工大學, 2011.

[13] 孟紅磊. 改性雙基推進劑裝藥結構完整性數值仿真方法研究 [D]. 南京: 南京理工大學, 2011.

[14] 鄧斌, 申志彬, 謝燕, 等. 含損傷粘彈性本構及其在有限元分析中的實現 [J]. 推進技術, 2013, 34(5): 699-705.

Transient Structural Integrity Analysis of Single Chamber Dual Thrust Engine Charge

GONG Jianliang,FAN Xuezhong,LI Hongyan,WANG Zhong

(Xi’an Modern Chemistry Research Institute, Xi’an 710065, China)

For the structural integrity of single chamber dual thrust engine charge under low temperature ignition condition, using incremental finite element method to solve the finite element model of thermal viscoelastic damge, the stress-strain field of internal charge was obtained. Research showed that in curing temperature, artificial debond layer had stress release effect on the head and tail of charge, to avoid the interface between the charge and the insulation layer. Meanwhile, the part which had larger Mises stress value charge was the parts of the wingtip transition and cylindrical surface. At the ignition time, the part which had large value of the charge hoop strain was the surface of the cylinder section. Finally, this method could be used to guide the design and safety evaluation of engine charge.

solid rocket motor; viscoelasticity; constitutive relation; structural integrity; strain softening

2015-12-22

國家自然科學青年基金(11501049)資助

龔建良(1986-),男,福建福安人,博士,研究方向:固體火箭發動機設計與仿真。

V435.21

A