汽車空調送風格柵優化與乘員熱舒適性改進

唐江明,　谷正氣,2,　莫志姣,　文　琪,　張　沙

(1.湖南大學 汽車車身先進設計制造國家重點實驗室,湖南 長沙 410082; 2.湖南工業大學 機械工程學院,湖南 株洲412007; 3.湖南大學 土木工程學院,湖南 長沙 410082)

?

汽車空調送風格柵優化與乘員熱舒適性改進

唐江明1,谷正氣1,2,莫志姣3,文琪1,張沙1

(1.湖南大學 汽車車身先進設計制造國家重點實驗室,湖南 長沙 410082; 2.湖南工業大學 機械工程學院,湖南 株洲412007; 3.湖南大學 土木工程學院,湖南 長沙 410082)

摘要:文章綜合考慮太陽輻射以及人體散熱對乘員艙熱環境的影響,以汽車空調風道雙葉片型出風口的水平格柵和垂直格柵的角度為設計變量,利用當量溫度作為熱舒適評價指標,將人體的頭部、胸部、左小腿、右小腿的當量溫度定義為設計目標;通過設計實驗DOE(design of experiment)選取30個樣本點,采用Kriging模型建立近似模型,最后利用連續二次規劃法(NLPQL)對該近似模型進行優化設計。優化結果表明駕駛員上身部位的當量溫度有明顯降低,其中頭部降低1.78 ℃,胸部降低1.43 ℃,駕駛員的熱舒適性得到顯著提高;同時也表明汽車空調送風格柵角度對乘員艙內流場及乘員熱舒適性有明顯的影響,在今后的熱舒適性研究中不可忽略。

關鍵詞:空調風道;計算流體動力學CFD;設計實驗;連續二次規劃法;熱舒適性

在汽車駕駛室等相對封閉的環境下,熱舒適性對于人體有重要的影響[1]。良好的熱舒適性環境能降低司機及乘客旅途的疲勞程度,不僅保證了行駛的舒適性,還確保了安全性。駕駛室內的熱舒適性與室內的流場分布有密切的關系,而室內空氣的流場分布一定程度上決定于空調出風口的設計[2]。因此,開展汽車空調出風口對乘員艙熱舒適性的影響研究是必要的。現在對于汽車燃油經濟性的要求越來越高,所以在保證汽車空調制冷能力一定的情況下從汽車空調風道以及出風口進行優化來提高乘員的熱舒適性具有非常重要的工程意義。

隨著計算機和數值技術的快速發展,一些研究者通過對空調風道中氣流的流動進行CFD仿真分析,進而對風道系統提出改進措施的研究,利用CFD方法進行乘員艙熱舒適性的研究也較多。文獻[3]重點研究出風口風速、風口尺寸和安裝位置對乘員艙熱舒適性的影響;文獻[4]研究了不同的太陽入射角度對乘員熱舒適性的影響；文獻[5]以空調風道中所加導流片的3個結構尺寸為設計變量,以駕駛員一側的出風量比例和總出風量為優化目標,對空調風道進行優化改進。但已有的研究大多是憑經驗對空調風道系統進行結構上的改進，對乘員艙的熱舒適性進行仿真分析時沒有將整個空調系統以及出風口考慮在內。

由于空調出風口格柵是通過改變送風方向來影響乘員艙內的氣流組織,從而對乘員的熱舒適性產生影響,因此在乘員艙舒適性仿真分析中考慮空調出風口的格柵角度是必要的。本文以此為基礎,將空調系統和乘員艙作為一個整體，并加入駕駛員模型,利用計算流體動力學軟件Fluent對汽車空調風道和乘員艙的氣流進行數值仿真;以連續二次規劃法NLPQL為優化設計工具,以人體對熱相對敏感部位的當量溫度為設計目標,建立相關的近似模型,分析了近似模型與實際仿真結果之間的誤差,最終對乘員的熱舒適性進行分析。

1CFD模型及計算方法

1.1太陽輻射模型

太陽位置由2個角度表示,即太陽高度角β和太陽方位角α。太陽高度角是太陽方向與水平面的夾角,太陽方位角是太陽方向的水平投影偏離南向的角度,示意圖如圖1所示。

太陽高度角β和方位角α的計算公式為:

β=arcsin(cosφcoshcosδ+sinφsinδ)

(1)

(2)

其中,φ為地球上某點的緯度;h為時角(東經時為正,西經時為負);δ為太陽赤緯。

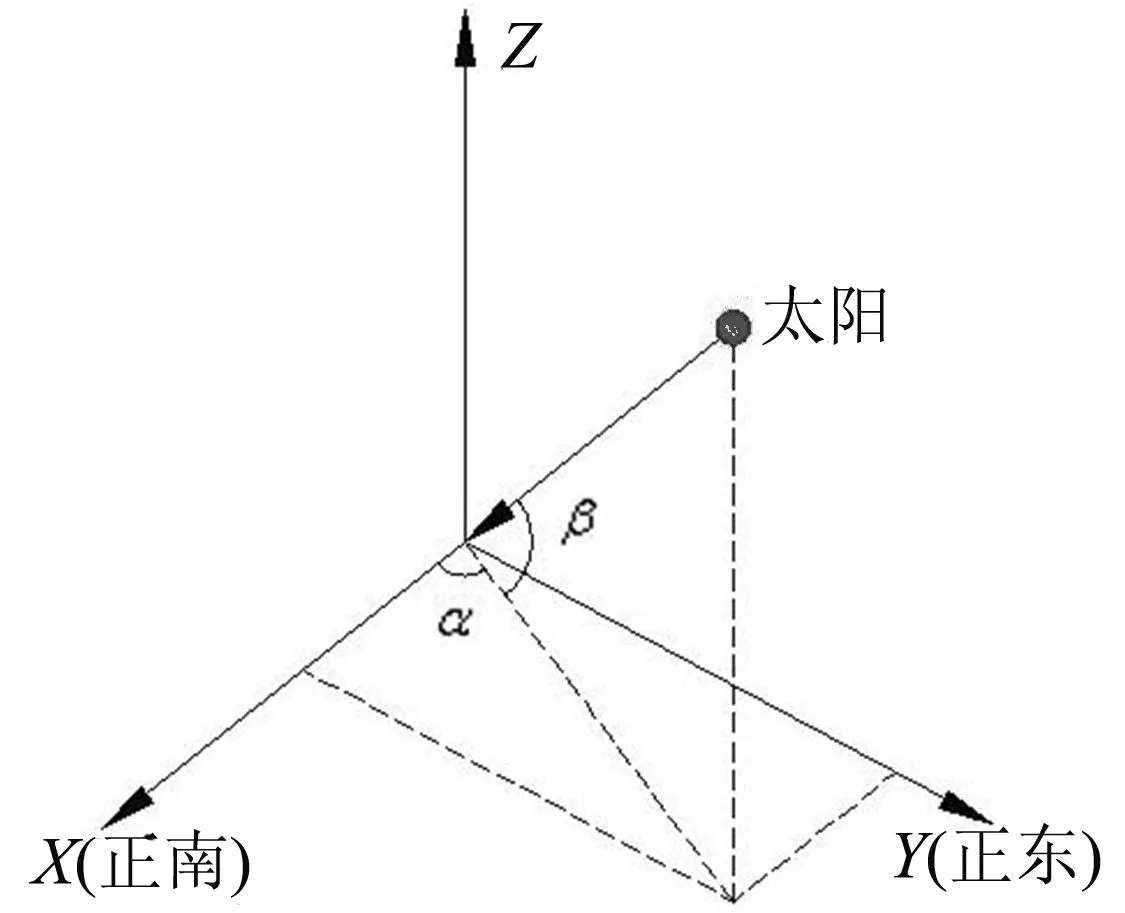
圖1　太陽高度角和方位角示意圖

太陽輻射熱量的大小用太陽輻射強度I來表示,單位為W/m2。在地球上任一傾斜表面上受到的直射輻射強度和散射輻射強度之和構成了該表面所接受的太陽總輻射強度。

1.2物理模型

以某三廂雙排轎車為研究對象,駕駛室內只有駕駛員1人,本文重點研究駕駛員的熱舒適性優化問題。利用UG4.0進行建模,由于發動機艙、后備箱以及車輪對車廂內流場沒有影響[6],特對物理模型進行簡化,簡化后的模型如圖2所示。

圖2　帶有人體模型的整車模型

駕駛室內的空調采用4出口式標準汽車空調風道模型,風道結構為對稱設計,在UG4.0中建立模型,如圖3所示。

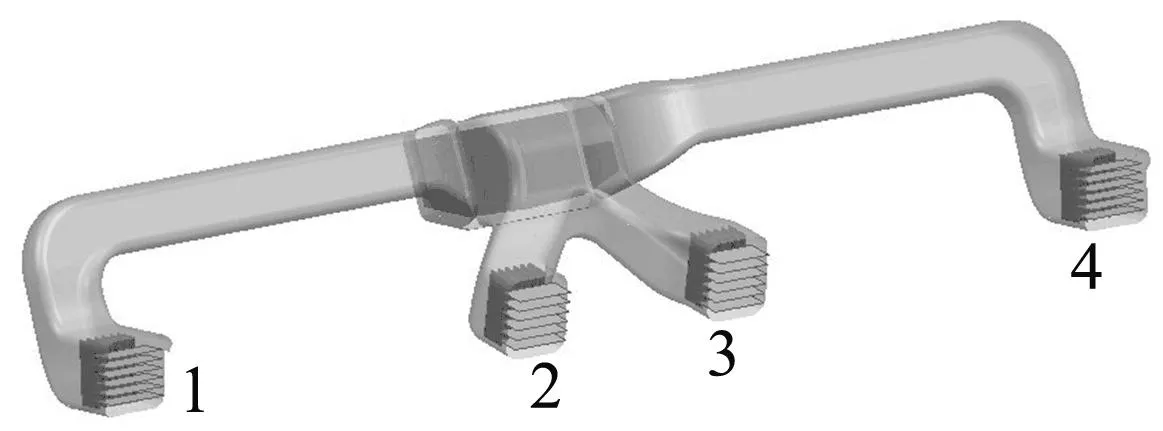
圖3　帶有格柵的空調風道UG模型

圖3的4個出風口中,1和4為上身出風口,2和3為全身出風口。本文中出風口結構采用的是應用廣泛的雙葉片型,它有2套不同方向的、可動的格柵,即水平格柵和豎直格柵。根據該出風口的尺寸以及相關文獻對格柵布置的要求,同時為了實現數值仿真,將格柵葉片簡化為片體,建立格柵模型。

1.3網格劃分及邊界條件設置

本文對駕駛室內部整個計算域的網格劃分是在前處理軟件ICEM中完成的,在劃分網格的過程中,考慮到空調風道和整個駕駛室內部的復雜結構,采用非結構化四面體網格。為了保證網格質量,全局網格及面網格大小的設定顯得十分重要。網格越小,越能貼合汽車表面,計算精度也越高,但網格太小,又會造成網格數量巨大,計算時間延長,甚至由于計算機硬件的限制無法生成網格。所以在一些比較平整或者曲率比較大的平面,可以適當設定大的網格;在某些尖銳曲面或者曲率較小、參數變化梯度大的平面,應適當減小網格尺寸。網格劃分結果如圖4所示。

圖4　網格劃分結果

為了模擬室外溫度較高條件下空調的制冷能力,本文模擬的地理位置選擇在長沙,時間為6月23日正午12：30,太陽透過率為0.8。轎車行駛速度為60 km/h,外部環境溫度為40 ℃,駕駛員衣服熱阻為0.5 clo(1 clo=0.155 m2·℃/W)。利用Discrete Ordinates輻射模型加入太陽輻射。經計算,此時太陽方位角α和太陽高度角β的理論計算值分別為-10.58°和85.44°,太陽直接輻射強度為707.467 W/m2,漫射太陽輻射強度為273.494 W/m2,地面反射強度為100.053 W/m2。

對送風口統一采用質量流量邊界條件,流量大小為0.110 5 kg/s,送風方向為垂直入口平面,出風口的格柵角度由樣本點確定,送風口溫度為20 ℃,回風口為壓力出口,相對壓強為p=0 Pa。邊界條件設置見表1所列。

表1　邊界條件設置

本文對除玻璃外的其他各壁面的熱輻射參數中，BC Type選項均設置為不透明壁面,玻璃設為半透明壁面。

發動機艙及與其相連的汽車前部的熱力學邊界設定為第3類邊界條件,即可以同時設定對流及外部輻射邊界條件。由于熱量是從發動機艙直接傳入駕駛室的,所以將發動機的冷卻水溫度當作自由流溫度,并綜合考慮發動機體本身以及汽車前壁面與冷卻水體之間空間的熱阻,將等效壁面換熱系數設定為20 W/m2。

對于人體的熱力學邊界條件,確定起來比較困難。首先,人的高矮、胖瘦、性別、年齡的差異和著裝直接影響人體表面熱力學邊界條件的取值;其次,人體本身為適應環境的自我調節作用無法考慮到數值計算中去,而人體皮膚表面的溫度和通過皮膚的熱流密度直接決定著人體熱舒適性。相關研究表明,采用第2類邊界條件較為合理。故本文將人體熱力學邊界設定為第2類邊界條件,設定皮膚表面散熱熱流密度為20 W/m2。

2優化設計

2.1熱舒適性評價

汽車乘員艙是一個微環境,所受的熱源眾多,而且太陽輻射分布不均,乘員艙內的溫度與速度變化梯度大,熱環境很不均勻。因此本文中選擇當量溫度Teq,i作為熱舒適性評價指標。當量溫度Teq,i包括了傳熱、對流換熱、熱輻射以及太陽輻射對人體的影響,同時也能反應出人體的不同部位對溫度的敏感度。

首先將駕駛員人體分為16個節段,再分別對不同節段進行熱舒適性評價。Teq,i的計算公式為:

其中,i為人體的節段;Teq,i為第i節段的當量溫度;Ts,i為第i節段的表面溫度;vair,i為第i節段周圍的空氣速度;Si為第i節段的表面面積;Ta,i為第i節段周圍的空氣溫度;σ為斯蒂芬-波爾茲曼常數;εi為第i節段的發射率;fi,n為第i節段對部件表面的角系數;Ti為第i節段的溫度；Tn為汽車乘員艙內部件的溫度;Qsol為人體得到的太陽輻射;hcal,i為在標準環境下感受器標定的第i節段的對流換熱系數[7]。

2.2設計變量

在UG4.0中對出風口的格柵進行建模。首先根據出風口的高寬比確定主格柵為水平葉片;再根據相關數據對葉片尺寸、葉片數目以及葉片間距的要求規定本文所建立格柵模型葉片數目為6,葉片長為80 mm,寬為30 mm,葉片間距為10 mm。格柵模型及設計參數如圖5所示。

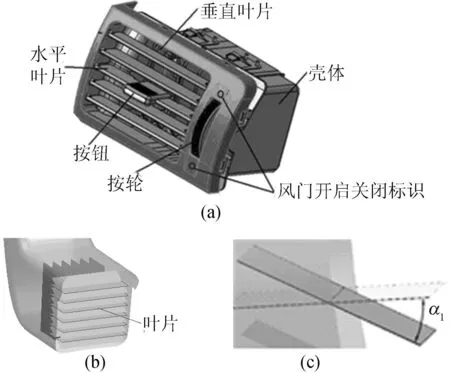
圖5　格柵模型及設計參數示意圖

在駕駛員左側的上身出風口,根據人機工程學相關數據以及實際物理模型確定其水平格柵相對于初始位置的調節幅度為[-30°,0°],垂直格柵的調節幅度為[-10°,30°]。同理,確定駕駛員右側的全身出風口水平格柵調節幅度為[-40°,10°],垂直格柵的調節幅度為[-30°,10°]。

4個設計變量如下:α1為上身出風口的水平格柵角度(向上為正),α2為全身出風口的水平格柵角度(向上為正),β1為上身出風口的垂直格柵角度(向右為正),β2為全身出風口的垂直格柵角度(向右為正)。所有格柵無偏轉角度，即α1、α2、β1、β2均為0時為初始位置。

采用DOE((designofexperiment))方法中的拉丁超立方方法確定30組設計樣本點,做出不同的格柵模型,將其導入ICEMCFD14.0中進行網格劃分,最后將網格文件導入Fluent求解器計算得出30組樣本數值。在進行目標優化時,選取當量溫度作為熱舒適性的評價指標;再根據“頭涼腳暖”的原則,即駕駛員的頭部溫度過高會引起頭暈、心情躁動,胸部溫度過高會使人感覺胸悶、心情煩躁,從而影響駕駛安全性,所以頭部當量溫度和胸部當量溫度的目標權重分配較大,分別為0.4和0.3,左小腿當量溫度和右小腿當量溫度目標權重都為0.15。 優化問題描述如下:

minf=ω1Teq1+ω2Teq2+ω3Teq3+ω4Teq4,

s.t.α1∈[-30°,0],α2∈[-40°,0],

β1∈[-10°,30°],β2∈[-30°,10°]。

其中,Teq1、Teq2、Teq3、Teq4分別為頭部、胸部、左小腿、右小腿的當量溫度;ω1、ω2、ω3、ω4為權重系數,分別取0.4、0.3、0.15、0.15。

2.3連續二次規劃法(NLPQL)

連續二次規劃法(NLPQL)用于解決帶有約束的非線性數學規劃問題,并假設目標函數和約束條件是連續可微的。序列二次規劃法(SQP)是NLPQL的核心算法。將目標函數以二階泰勒級數展開,并把約束條件線性化,原非線性問題則轉化為一個二次規劃問題,通過解二次規劃得到下一個設計點,然后根據2個可供選擇的優化函數執行一次線性搜索,其中Hessian矩陣由BFGS公式更新[8]。

3計算結果與分析

3.1建立響應面模型

對計算出來的30組樣本結果采用Kriging模型方法建立近似模型。選取最優樣本點的CFD仿真值和近似模型響應值進行驗證,其最優點的設計參數值見表2所列。

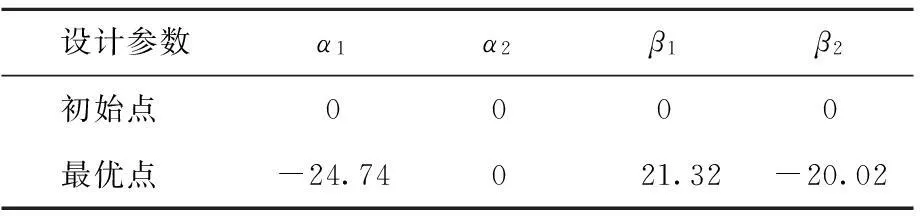
表2　初始點與最優點設計參數值　(°)

根據最優點建立相應的UG模型進行CFD仿真計算,得出的數值與近似模型得出的結果誤差僅為-0.37%、-1.44%、1.11%和-0.03%,見表3所列。由表3可知,CFD的計算值與近似模型的值相差均在2%以內,可信度較高。因此,直接用近似模型的值來代替CFD的計算值是可行的。

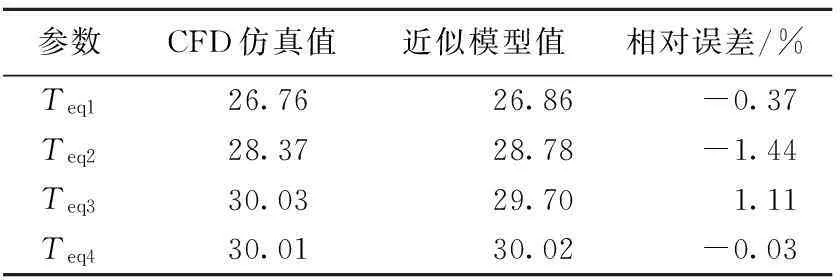
表3　最優點仿真值與近似模型響應值對比　℃

3.2優化結果分析

優化前、后乘員艙內部速度流線圖如圖6所示。由圖6可以看出,格柵對汽車空調出風口的送風有明顯的導流作用,乘員艙內部流場在優化前、后有明顯的區別。駕駛員側的空調出風口的格柵處于原始角度時,經空調系統送入車室內的冷風集中繞過駕駛員頭部送至后排區域,造成冷風與駕駛員沒有進行充分的熱交換,散熱效果不理想,從而造成駕駛員上身部位的體表溫度相對較高;優化后的乘員艙內部流場組織更加合理,經空調出風口直接送至駕駛員上半身部位的冷風比例明顯增大,這樣會使冷風與駕駛員上身部位有更加直接并且充分的熱交換過程,從而使駕駛員頭部和軀干部位的熱量被冷風更多地帶走,駕駛員的散熱效果比初始條件有明顯的提高。

圖6　優化前、后艙內速度流線圖(下為優化后)

通過Fluent軟件仿真得出的人體表面溫度分布云圖如圖7所示。

從圖7可以看出,優化后由于駕駛員的上身部分冷風風量比例增大,所以駕駛員頭部和軀干部位的溫度比優化前有明顯降低,人體散熱效果得到了改善。

優化前、后設計目標值對比見表4所列。由表4可知,在左小腿和右小腿的當量溫度沒有升高的情況下,頭部和胸部的當量溫度顯著降低,分別降低了1.78 ℃和1.43 ℃,滿足了“頭涼腳暖”的原則[9-10],熱舒適性得到了提高。

人體各部位熱舒適性示意圖如圖8所示。

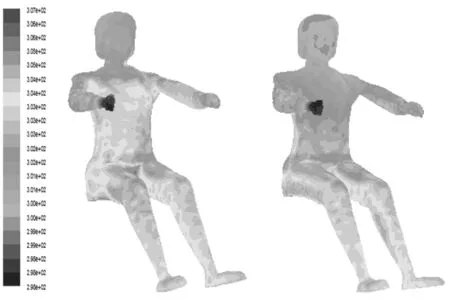
圖7　優化前、后人體表面溫度分布云圖(右為優化后)

℃

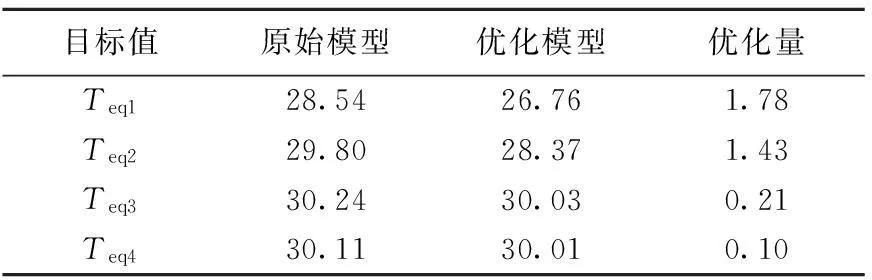
溫度

從優化前、后的對比可知,人體各部位的當量溫度都有所降低,在下身部位溫度降低很小的情況下,上身部位溫度下降明顯,其中軀干部位溫度大約下降1 ℃,頭部溫度下降1～2 ℃,顯然滿足

本文提出的“頭涼腳暖”的優化目的,同時駕駛員的人體熱舒適性得到了較大改善。

4結論

本文通過流體計算軟件Fluent對車室內的熱環境進行了仿真計算,綜合考慮了太陽輻射以及人體散熱的影響,重點研究汽車空調出風口格柵角度對駕駛員熱舒適性的影響,在此基礎上利用ISIGHT軟件對出風口的格柵角度進行優化,優化結果表明車室內的乘員熱舒適性得到了明顯的改善。具體結論如下:

(1) 建立的響應面模型通過CFD仿真值的驗算,誤差在2%以內,近似質量非常高,表明可以代替實際的仿真計算分析,提高了計算效率。

(2) 優化后的設計變量參數應用于駕駛員熱舒適性分析,駕駛員上身部位的當量溫度都有所降低,其中人體對于熱相對敏感的頭部和軀干部位降低了將近2 ℃,同時車室內的氣流組織更加合理,駕駛員的熱舒適性得到了明顯改善。

(3) 汽車空調雙葉片型出風口格柵角度對乘員艙內流場組織及乘員的熱舒適性有顯著影響。

[參考文獻]

[1]谷正氣.汽車空氣動力學[M].北京:人民交通出版社,2005:5-6.

[2]Kai A, Proksch C, Zipf N,et al.Thermal comfort increase through advanced airflow analysis，SAE Paper 2005-01-2001 [R].SAE,2005. doi:10.4271/2005-01-2001.

[3]Shojaee M, Tehrani F,Noorpoor A,et al. Analysis of vehicle passenger compartment HVAC using simulation,SAE Paper 2004-01-1505[R].SAE,2004.doi:10.4271/2004-01-1505.

[4]江濤，谷正氣，楊易，等.太陽幅射對乘員熱舒適性影響的研究[J].合肥工業大學學報：自然科學版，2011,34(8):1135-1137,1159.

[5]谷正氣,申紅麗,楊振東,等.汽車空調風道改進及對乘員熱舒適性影響分析[J].重慶理工大學學報,2013,36(8):91-97.

[6]谷正氣,孟慶超, 楊易,等.轎車室內流場的數值模擬研究[J]. 系統仿真學報, 2008, 20(7):1700-1702.

[7]靳艷梅,王保國,劉淑艷.車室人體熱舒適性的計算模型[J].人類工效學,2005,11(2):16-19.

[8]李偉湘.基于二次規劃法的連續體結構拓撲優化方法及其應用研究[D].長沙:長沙理工大學,2010.

[9]Han T,Chen K H. Assessment of various environmental thermal loads on passenger compartment soak and cool-down analyses，SAE Paper 2009-01-1148[R].SAE,2009.doi:10.4271/2009-01-1148.

[10]倪冬香.基于人體熱調節模型的轎車乘員艙熱舒適性分析[D].上海:上海交通大學,2010.

(責任編輯胡亞敏)

Optimization of vehicle air-conditioning grilles and the improvement of passenger thermal comfort

TANG Jiang-ming1,GU Zheng-qi1,2, MO Zhi-jiao3,WEN Qi1,ZHANG Sha1

(1.State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha 410082, China; 2.College of Machanical Engineering, Hunan University of Technology, Zhuzhou 412007, China; 3.School of Civil Engineering, Hunan University, Changsha 410082, China)

Abstract:By using the horizontal and vertical blades angle of vehicle air-conditioning outlet as design variables, considering the effect of solar radiation and body heat dissipation on the cab thermal environment, and taking the equivalent temperature as thermal comfort index, the equivalent temperatures of human head, chest, left shank and right shank are defined as optimization objectives. An approximate model is built by using Kriging model based on thirty sample points which are selected by the method of design of experiment(DOE). Finally, the approximate model is optimized by using Sequential Quadratic Programming-NLPQL. The result shows that the equivalent temperature of driver’s upper body is reduced obviously, the head temperature by 1.78 ℃ and the chest temperature by 1.43 ℃. The thermal comfort of the driver is obviously improved. It is shown that the blade angle of vehicle air-conditioning outlet has significant influence on the flow field of the cab and the thermal comfort of passengers, so it can not be ignored in the future research on the passenger thermal comfort.

Key words:air-conditioning duct; computational fluid dynamics(CFD); design of experiment(DOE); sequential quadratic programming(SQP) method; thermal comfort

中圖分類號:U463.851

文獻標識碼：A

文章編號：1003-5060(2016)03-0309-06

doi:10.3969/j.issn.1003-5060.2016.03.004

作者簡介：唐江明(1990-),男,湖南長沙人，湖南大學碩士生;谷正氣(1963-),男,湖南長沙人，博士,湖南大學教授,博士生導師.

基金項目：中央財政支持地方高校專項資金資助項目(0420036017);湖南大學汽車車身先進設計與制造國家重點實驗室自主課題資助項目(734215002)

收稿日期：2015-01-17；修回日期：2015-06-11