304不銹鋼板材噴丸強化處理最佳工藝參數研究

趙　韓，　朱仁勝，　張　月，　周　隱，　孫　程，　劉四洋

(合肥工業大學 機械與汽車工程學院，安徽 合肥　230009)

?

304不銹鋼板材噴丸強化處理最佳工藝參數研究

趙韓，朱仁勝，張月，周隱，孫程，劉四洋

(合肥工業大學 機械與汽車工程學院，安徽 合肥230009)

摘要:文章運用ANSYS/LS-DYNA建立了304不銹鋼板材多丸噴丸硬化處理的有限元模型,模擬了不同噴丸參數(彈丸的速度、半徑和強度)對304不銹鋼板材殘余應力的影響規律。先計算不同層深的平均殘余應力值,以得到不同參數下最大殘余應力場;再對模擬結果采用逐步回歸分析法建立殘余應力關于工藝參數的最優回歸方程,從而獲得了最大殘余應力隨不同參數的變化圖,并通過殘余應力測試對上述方程進行了驗證。結果表明:數值計算所得最優回歸方程計算結果和實驗結果相符,可據此針對所需的最大殘余應力要求確定噴丸工藝參數,為工程實踐提供依據。

關鍵詞:304不銹鋼；噴丸；殘余應力；有限元；工藝參數；逐步回歸

噴丸強化是一種效果卓著的金屬零件表面形變強化工藝,是提高工件疲勞壽命的有效途徑之一,具有實施方便、效果顯著、適應面廣、消耗低等特點,被廣泛應用于航空、軍工、汽車等領域。

現有噴丸工藝參數的選擇大都依靠經驗或試噴的方法作出多個S-N曲線進行比較,找出最佳曲線,進而選擇噴丸工藝參數。采用經驗缺少科學依據,采用實驗方法非常復雜、周期長并且昂貴。而數值計算因其經濟性和高效性成為研究噴丸強化的重要手段,可以節省實驗的巨大投入[1]。已有許多研究者進行了數值計算研究，文獻[2]首先對噴丸過程進行了有限元準動態模擬,僅考慮了彈丸的慣性作用;文獻[3]建立了二維軸對稱噴丸動態模型,并針對雙丸粒發展了準靜態三維有限元模型;文獻[4]對噴丸殘余應力進行了動態有限元研究,但是僅限于單丸碰撞;文獻[5]用三維軸對稱模型模擬噴丸過程,也僅限于單丸碰撞;文獻[6]把噴丸過程的三維有限元數值模擬研究推進到與實際更為接近的多丸粒階段;文獻[7]采用LS-DYNA代碼研究多丸粒噴丸過程的數值模擬,并得出結論——受噴靶體的殘余應力分布與彈丸速度和粒數密切相關;文獻[8]應用ABAQUS/Explicit的控制方程建立噴丸硬化過程的準動態顯示模型,但僅模擬了單丸碰撞。

關于噴丸強化機理，文獻[9]提出至少有應力強化和組織結構強化2種噴丸強化機制。然而,目前仍然缺乏相關的知識對噴丸過程的參數進行最優設計。

本文運用ANSYS/LS-DYNA平臺并采用分段線性材料函數模型,建立了多丸粒沖擊304不銹鋼板材的噴丸過程的有限元模型;并模擬計算了不同彈丸半徑、速度、強度下304不銹鋼靶體的殘余應力沿層深的變化規律。進而采用正交試驗法安排多參數(包括彈丸半徑、速度、強度)進行數值計算,運用多項式逐步回歸方法求得最優回歸方程,得出關于殘余應力的最佳工藝參數表達式。

1有限元模型的建立

在ANSYS/LS-DYNA平臺上,首先建立實體模型如圖1所示，取1/4實例模型進行有限元模擬計算,有限元模型如圖2所示，邊界條件設置如圖3所示。

圖1　實體計算模型　　　　　　　　　　圖2　有限元模型　　　　　　　　　圖3　邊界條件設置

定義R為球體半徑,則靶體材料尺寸為6R×6R×2.1 mm,設置100%噴丸覆蓋,如圖1所示。彈丸第1層緊貼靶材并以第1層為參照系；第2層彈丸在第1層彈丸基礎上-x及y方向分別平移R；第3層彈丸在第2層彈丸的基礎上在x方向平移R；第4層彈丸在第3層彈丸基礎上在-x及-y方向分別平移R。對實體模型進行網格劃分,模型單元選用SOLID164顯式動力分析單元,碰撞區域網格加密設置為0.08R×0.08R,碰撞區域為4R×4R。由于板材和彈丸的對稱性,為了降低單元數量和節省計算時間,僅取1/4的實體模型作為噴丸處理有限元模擬的計算模型,網格劃分除碰撞區域外設置得越來越稀疏,如圖2所示。

考慮靶體尺寸對模擬效果的影響,在靶體側面施加非反射邊界條件;XOZ面及YOZ面為對稱面,在這2個面上施加對稱邊界條件;在底面施加固定約束以減小震蕩,如圖3所示。為了提高模擬的真實可靠性,對靶體和彈丸材料采用分段線性材料模型。304不銹鋼和噴丸模型材料參數如下：楊氏模量為193 GPa，泊松比為0.3，密度為7.93 g/cm3，屈服強度為300 MPa，切線模量為74.23 GPa。

2有限元分析

取彈丸半徑0.3 mm,速度80 m/s,彈丸屈服強度300 MPa,根據前面的建模、加載計算,選取X方向主應力σxx,如圖4所示,噴丸之后靶體發生塑性變形,隨著距表面層深的增加,靶體殘余應力先增大后減小,在0.06 mm左右達到最大殘余壓應力342 MPa。因此,靶體內部最大殘余壓應力不在受撞擊表面而是表面稍下方,這一點與工程實際吻合。隨著噴丸時間的增加,最先形成的彈坑受到后續彈丸撞擊后面積減小,在這些彈坑下方未出現最大壓應力,可以預見,經過多次反復噴丸后,靶體內部殘余壓應力分布逐漸趨于平均。以下所述的平均殘余應力和最大殘余應力皆是指對所在單元層的計算面積取平均。

圖4　半徑0.3 mm,速度80 m/s應力云圖

材料表面由于受彈丸反復撞擊擠壓,發生嚴重塑性變形,出現許多彈坑,使靶體表層表面積增大,部分區域出現拉伸應力,這種現象解釋了圖4表層部分區域出現正應力,同時也是表層殘余壓應力小于次表層的原因。隨著層深的增大,彈坑形成的拉應力逐漸減小,壓應力逐漸增加,呈現次表層殘余壓應力最大的現象,此后,隨著層深的進一步增加,彈丸撞擊擠壓靶體形成的壓應力對靶體影響逐漸減小,塑性變形量逐漸減小,因此,殘余壓應力也逐漸減小,直到未噴丸時的水平。

為了分析噴丸工藝參數對304不銹鋼板材的影響,下面建立最大殘余應力與3個參數(彈丸的半徑R、速度v、強度σs)之間的關系。本文采用正交試驗法安排噴丸工藝參數,取3因素4 個水平,選用L16 (43) 正交試驗表, 針對每一組噴丸工藝參數值建立三維實體模型,在ANSYS/LS-DYNA平臺上選用SOLID164顯式動力分析單元,進行網格劃分、設置邊界條件,并進行數值計算,得到相應的最大殘余應力值,見表1所列。

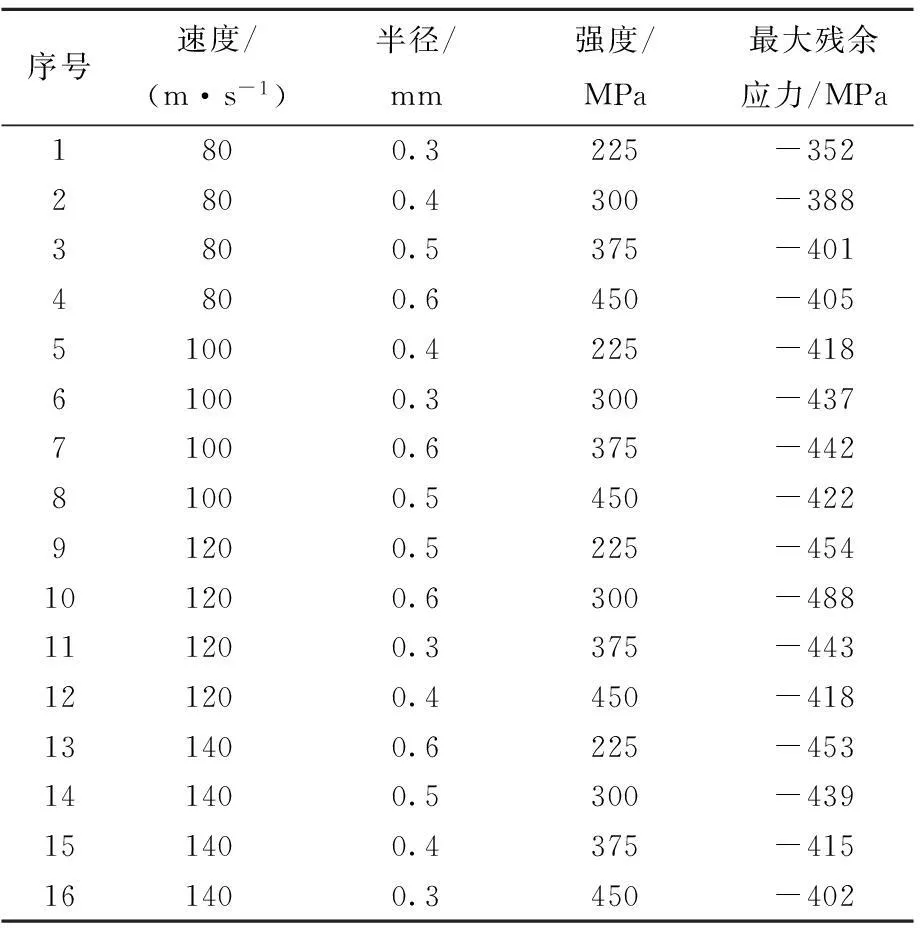
表1　按照正交實驗安排的工藝參數及計算結果

3逐步回歸分析

選擇3 種函數形態(一次、 二次、 三次多項式)進行逐步回歸分析[10], 求得回歸方程后進行比較, 選擇其中可信度和精度高并且簡單的回歸方程作為所求的數學模型。

304不銹鋼板材噴丸強化有R、 v 、σs3個輸入變量,1個輸出變量 (因變量) 為最大殘余應力。按正交試驗法安排的參數和計算得到的殘余應力計算數據, 取選入因子時顯著性檢驗的分布值 F0.25(1, 15)=1.41。剔除因子時顯著性檢驗的 F 分布值采用逐步回歸分析的標準計算程序進行計算,得到如下回歸方程 (置信度 A=0.25)。

一次多項式：

σxx=-284.1-0.716 3v-134.8R

(1)

二次多項式：

σxx=309.2-9.894v-0.920 5σs+

0.041 72v2-152.40R2+1.433×10-3σs2

(2)

三次多項式：

σxx=564.3-5.430v-4.932σs+0.013 73σs2+

1.270×10-4v3-217.7R3-1.215×10-5σs3

(3)

回歸方程中各變量系數保留的位數是根據該變量的有效數字選取的。通過對3個回歸方程的相關系數、F檢驗值、剩余平方和、標準偏差、殘差進行分析比較, 確定最優回歸方程為三次多項式的回歸方程(置信度A=0.25)，即(3)式。

仿真計算數據點和最優回歸方程的計算值輸出如圖5所示,由圖5可見,回歸方程的曲線較好地擬合了仿真計算數據點。

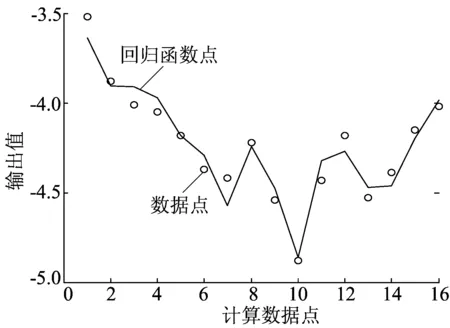
圖5　σxx模擬數據點和最優回歸點

根據最優回歸方程,可以對各自變量與最大殘余應力的關系做定量的分析，得到3幅最大殘余應力與因素變化的三維曲面圖，如圖6所示。

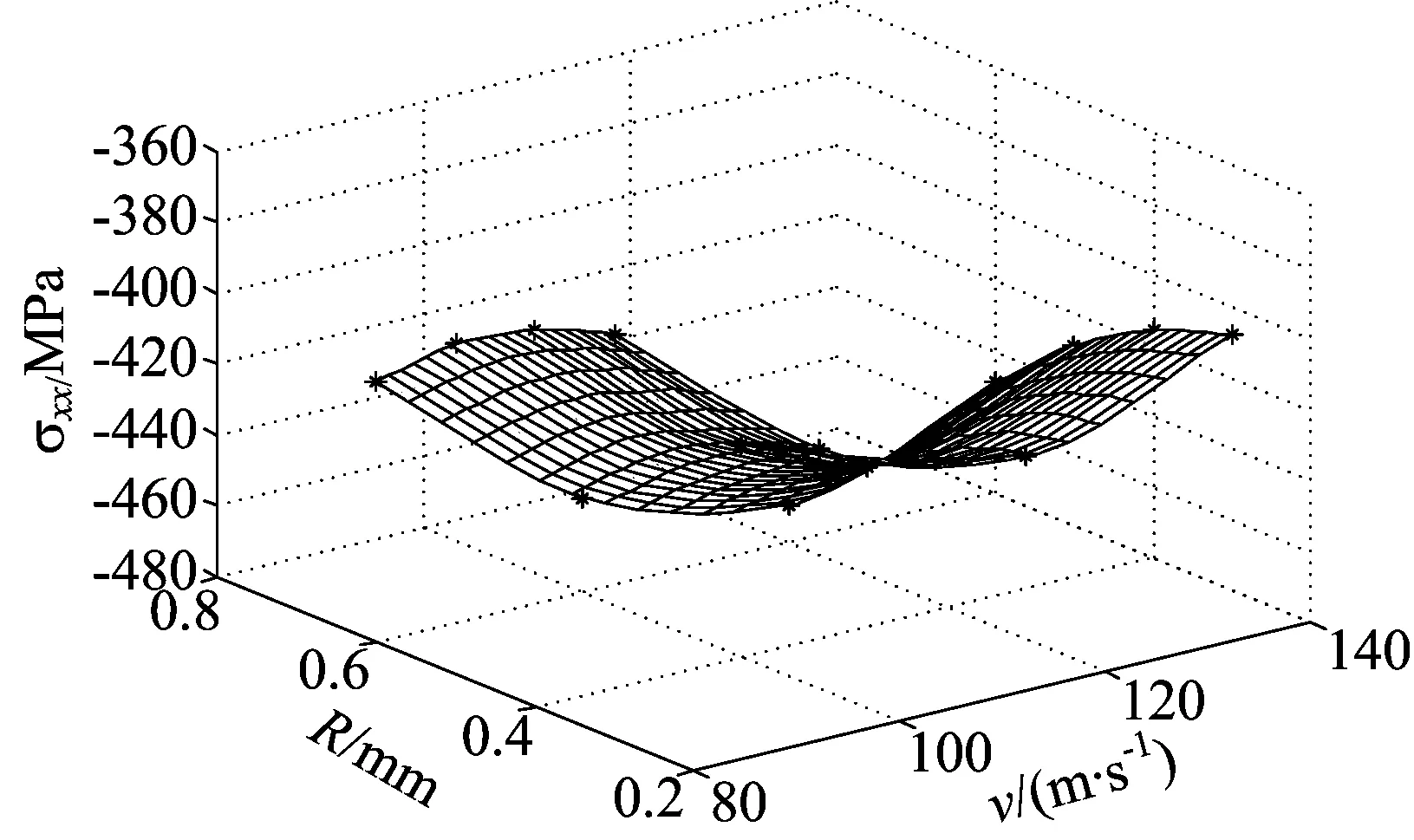
(a)　σxx-f(R,v)關系

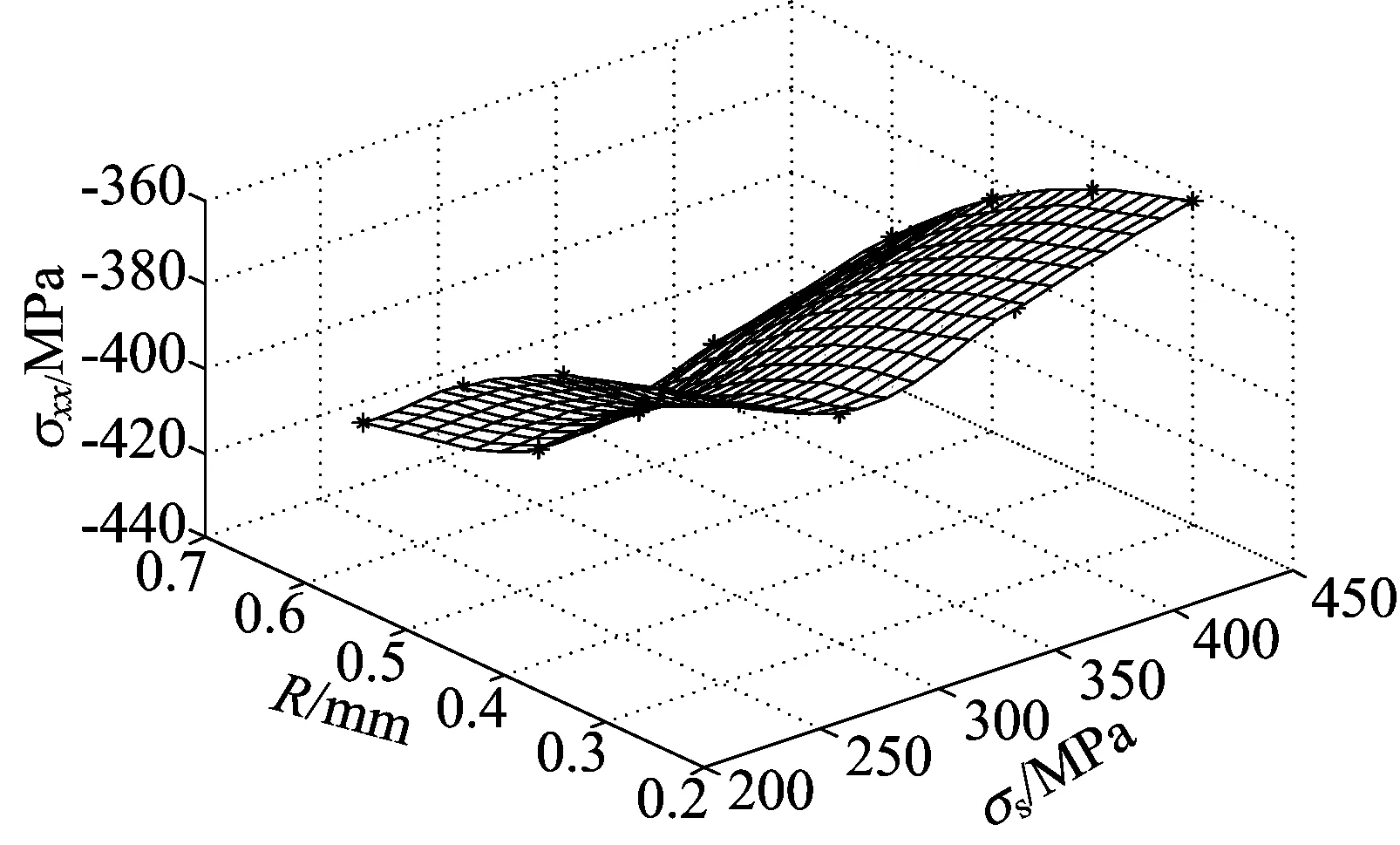
(b)　σxx-f(R, σs)關系

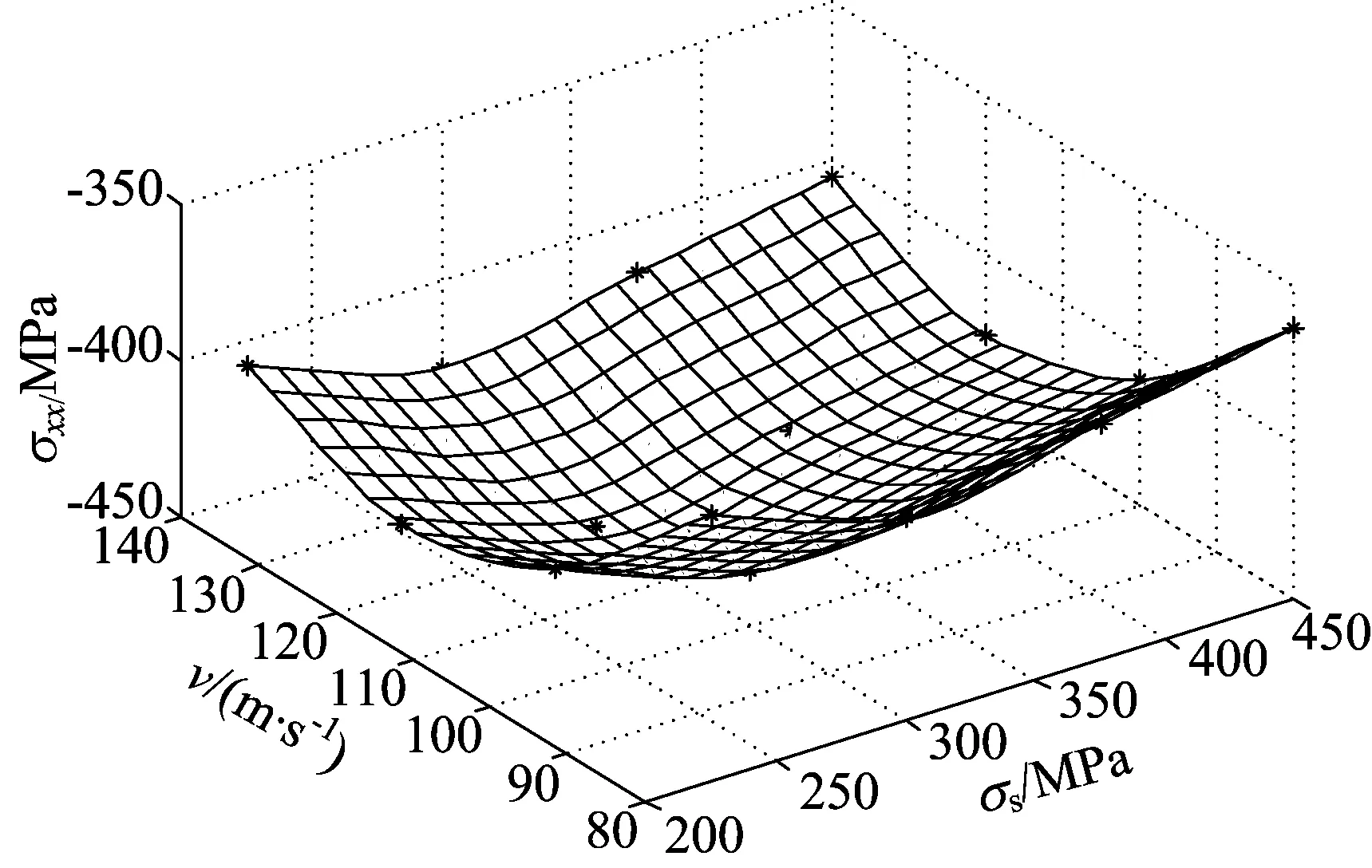
(c)　σxx-f(v, σs)關系

從圖6中可以分析任意2個自變量參數對σxx的相互匹配關系,增大彈丸半徑和彈丸速度,靶體材料的殘余應力會隨之先增大再減小。

最優回歸方程還可應用于生產實際中的工藝參數選擇,如某鏟運機大臂根據地下工作環境,大臂為304不銹鋼板材拼焊而成,需要噴丸強度達到最大殘余應力450 MPa,可選擇如下工藝參數：

工藝參數組1:令彈丸速度100 m/s,彈丸強度300 MPa,代入最優回歸方程,則求得噴丸半徑為0.495 mm。

工藝參數組2:令彈丸速度120 m/s,彈丸強度300 MPa,代入最優回歸方程,則求得噴丸半徑為0.362 mm。

當然根據噴丸強度、噴丸設備及相關可具備的工藝參數要求,還可根據最優回歸方程制定出更多的工藝參數組。

4實驗驗證

為了驗證模擬結果的正確性,采用實驗的方法對模擬結果進行驗證。對304不銹鋼板材進行噴丸處理。檢測條件：采用Proto-LXRD 型X 射線應力分析儀,檢測執行ASTM-E915-2010[11]、EN15305-2008[12]、 GB7704-2008[13]標準,電解拋光機型號為Proto-8818,采用飽和NaCl 水電解液,用數顯千分表檢測電化學腐蝕深度。采用G3不銹鋼彈丸,半徑0.6 mm,彈丸速度120 m/s、彈丸強度300 MPa,噴丸覆蓋率100%,利用X 射線應力分析儀檢測不銹鋼板噴丸殘余應力沿層深的分布。

在ANSYS/LS-DYNA上進行模擬計算,將模擬計算數值與實驗所得數據進行比較,如圖7所示。由圖7可見,模擬結果與實驗所測結果曲線十分吻合,說明模擬計算模型合理,最優回歸方程正確。

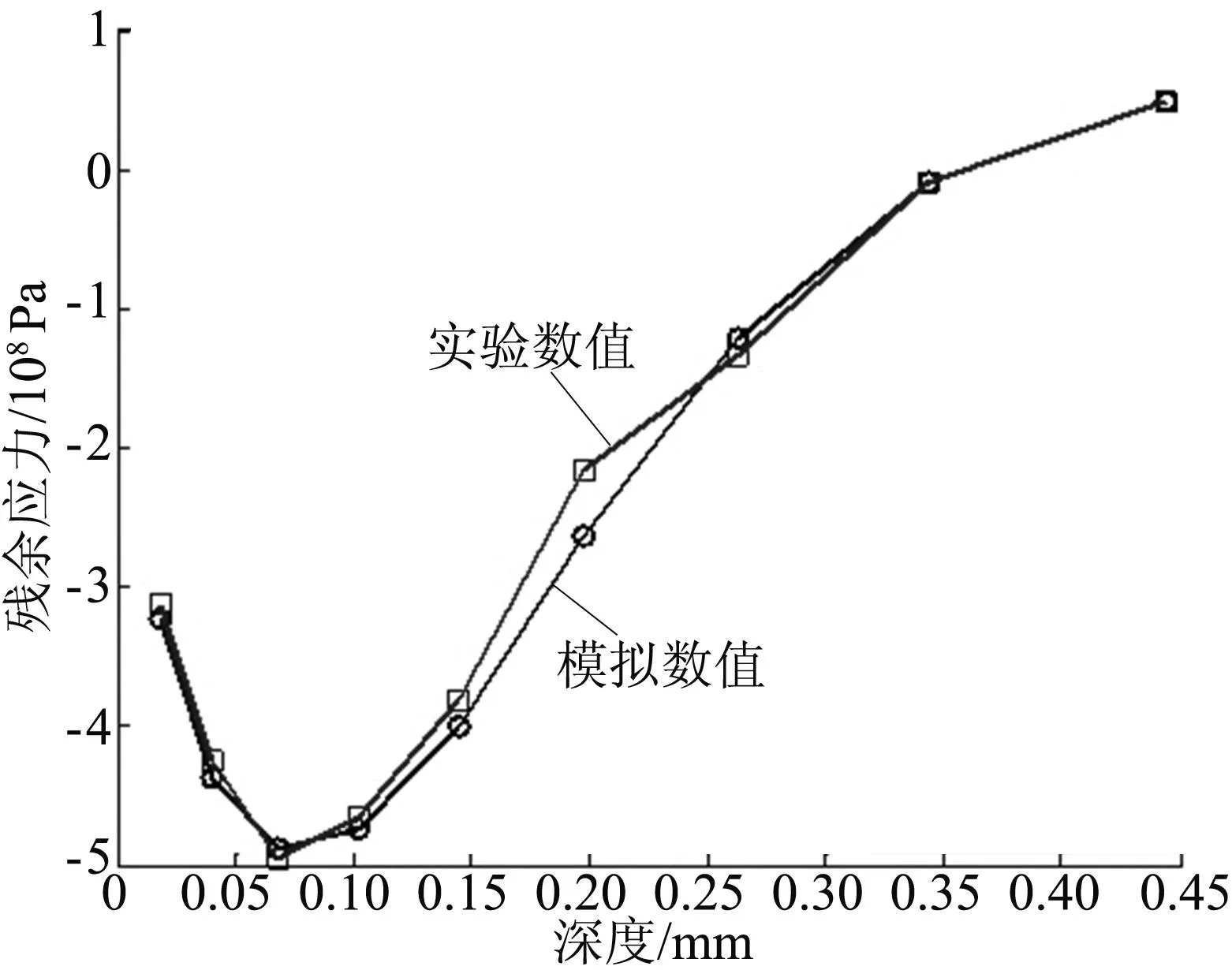
圖7　實驗驗證比較

5結論

本文采用ANSYS/LS-DYNA有限元方法模擬了304不銹鋼在不同彈丸速度、半徑以及強度的情況下的噴丸過程,得出噴丸后靶體形變層內平均殘余應力隨層深的變化關系,以及不同工藝參數下靶體內殘余應力的分布情況,再采用回歸分析對實驗結果進行討論,得出各參數對靶體內部最大殘余應力的影響,最后通過實驗驗證的方法驗證了有限元模擬是正確的。得到如下結論:

(1) 采用正交實驗安排噴丸工藝參數,運用逐步回歸分析方法進行回歸,最后得到最優回歸方程,計算結果與有限元分析結果一致,并與殘余應力實測結果相符,說明最優回歸方程是正確的。

(2) 采用最優回歸方程,分別固定彈丸速度或者半徑,可以得出單一影響因素下的最佳工藝參數。

[參考文獻]

[1]沈健,路永品,朱仁勝,等.MW 風力發電機齒輪動態數值計算[J].合肥工業大學學報: 自然科學版，2013，36(3):275-278.

[2]Johnson W.Impact strength of materials [M].London: Arnold，1972:323-337.

[3]Schiffner K，Helling C D G.Simulation of residual stresses by shot peening [J].Computers and Structures，1999，72:329-340.

[4]Meguid S A，Shagal G，Stranart J C.Finite element modeling of shot-peening residual stresses [J].Materials Processing Technology，1999，92/93:401-404.

[5]Baragetti S.Three-dimensional finite-element procedures for shot peening residual stress field prediction [J].International Journal of Computer Applications in Technology，2001，14: 51-63.

[6]Meguid S A，Shagal G，Stranart J C.3D FE analysis of peening of strain-rate sensitive materials using multiple impingement model [J].International Journal of Impact Engineering，2002，27:119-134.

[7]Majzoobi G H，Azizi R，Nia A A.A three-dimensional simulation of shot peening process using multiple shot impacts [J].Materials Processing Technology，2005，164/165:1226-1234.

[8]Shivpuri R，Cheng X M，Mao Y N.Elasto-plastic pseudo-dynamic numerical model for the design of shot peening process parameters[J].Materials and Design，2009，30:3112-3120.

[9]王仁智.金屬材料的噴丸強化原理及其強化機理綜述[J].中國表面工程,2012,25(6):1-9.

[10]白新桂.數據分析與試驗優化設計[M].北京: 清華大學出版社，1986：84-123.

[11]ASTM E 915-2010，檢測殘余應力測量用X射線衍射儀的準線的試驗方法[S].

[12]BS EN 15305-2008,無損檢驗：使用X射線衍射分析剩余應力的試驗方法[S].

[13]GB/T 7704-2008,無損檢測X射線應力測定方法[S].

(責任編輯馬國鋒)

Numerical investigation on the optimization of shot peening process parameters of 304 stainless steel sheet

ZHAO Han,ZHU Ren-sheng,ZHANG Yue,ZHOU Yin,SUN Cheng,LIU Si-yang

(School of Machinery and Automobile Engineering, Hefei University of Technology, Hefei 230009, China)

Abstract:In this paper, the finite element model of shot peening process for multiple shot impacts on 304 stainless steel sheet is developed by using ANSYS/LS-DYNA code. The model is applied to investigating the effects of shot velocity, radius and strength of shot material on the residual stress of target. Firstly, the averaged residual stresses along the depth of target are calculated and the maximum residual stresses are obtained. Secondly, the optimal regression equations of maximum residual stress as a function of shot velocity, radius and strength are determined by means of stepwise regression of numerical results. Consequently, the maximum residual stress profiles are plotted against two parameters when the third one is invariable. The change of maximum residual stress along with different parameters are obtained, and the results are validated by experiments. It is shown that the numerical results are in good agreement with the experimental ones, the parameters can be determined based on the needed maximum residual stress, and the result be applied to solving engineering problem.

Key words:304 stainless steel; shot peening; residual stress; finite element; process parameter; stepwise regression

中圖分類號:TG178

文獻標識碼：A

文章編號：1003-5060(2016)03-0320-05

doi:10.3969/j.issn.1003-5060.2016.03.006

作者簡介：趙韓(1957-),男,安徽滁州人,博士,合肥工業大學教授,博士生導師.

收稿日期：2015-01-15；修回日期：2015-03-13