基于全節點負荷斷面聚類的無功優化資產配置

桂前進,　黃　昊,　張大波,　孔德全

(1.國家電網安徽省電力公司 安慶供電公司,安徽 安慶　246003; 2.安徽工業大學 電氣與信息工程學院,安徽 馬鞍山　243032; 3.合肥工業大學 電氣與自動化工程學院,安徽 合肥　230009; 4.合肥天鷹高科技有限公司，安徽 合肥　230088)

?

基于全節點負荷斷面聚類的無功優化資產配置

桂前進1,黃昊2,張大波3,孔德全4

(1.國家電網安徽省電力公司 安慶供電公司,安徽 安慶246003; 2.安徽工業大學 電氣與信息工程學院,安徽 馬鞍山243032; 3.合肥工業大學 電氣與自動化工程學院,安徽 合肥230009; 4.合肥天鷹高科技有限公司，安徽 合肥230088)

摘要:文章提出了一種無功優化資產配置模型,綜合考慮投資無功補償裝置的費用和效益之間的平衡,將電壓目標、網損目標和投資目標全部轉化為費用進行優化。針對現有優化方法中負荷模型的缺點,提出全節點負荷斷面聚類方法,將僅能處理實向量的歐氏距離推廣到復數域的酉空間,給出全節點負荷復向量相似性度量方法及其K-means聚類的詳細步驟。基于PG&E69節點系統的算例驗證了所提模型的有效性。

關鍵詞:全節點負荷;復功率;聚類分析;無功優化;資產配置

0引言

電力系統資產配置需要在投資的收益和成本之間平衡,不但需滿足電網運行的技術標準,還需考慮投資的經濟性[1]。為了改善電壓質量和降低網損,需在電網中選擇合適的地點配置一定容量的無功補償裝置,國內外研究者作了大量研究并取得了豐碩的成果[2-6]。文獻[2]考慮了節點電壓偏差、三相電壓不平衡度、有功網損及發電費用4個方面,通過對其加權求和作為目標函數來研究含分布式電源的配電網無功優化問題。文獻[3]建立了主動配電網綜合無功優化模型,考慮了無功優化策略之間的優先次序。文獻[4]介紹了代替聯絡開關的新型電力電子裝置——基于軟常開開關(soft normally open point，SNOP),并給出了含SNOP的配電網優化運行模型。上述研究成果均考慮了通過無功補償來保證電壓水平的同時降低網損,卻沒有考慮無功補償裝置的投資費用。從投資角度來看,如果網損降低獲得的收益無法抵消無功補償裝置的投資費用,則是不經濟的,有可能造成不必要的浪費。

針對這一問題,文獻[5]以無功補償方案全壽命周期凈收益現值為目標函數,建立了多階段配電網無功規劃數學模型。這種方法全面考慮無功規劃方案的初始投資、運行維護成本、報廢成本,但是計算網損只考慮了單一負荷水平。在不同負荷水平下,系統對無功配置的需求可能存在很大差異,僅依據單一負荷水平進行無功配置,所得方案對其他負荷水平不一定是經濟的,也可能無法滿足電壓質量的要求,因此進行無功優化規劃時有必要考慮多種負荷水平的影響[6]。文獻[7-8]為了研究隨機出力的風電機組接入配電網的無功優化問題,將風機出力劃分為零輸出場景、欠出力場景及額定出力場景,然后將各風機場景進行組合得到系統場景,這種方法并未考慮負荷的變化。研究電力系統投資策略時,負荷水平的選取對研究結果有較大影響,為了更準確地反映系統運行情況,需選取不同斷面來進行研究。文獻[9]提出了基于K-means聚類分析的負荷模型斷面選取方法,提升了電力系統可靠性指標的計算精度。文獻[6]則基于聚類方法來選取系統運行斷面,并將其運用于無功優化過程中。然而,文獻[9]僅對系統有功負荷進行聚類,文獻[6]則僅對系統無功負荷進行聚類,而每個節點的負荷包含有功功率和無功功率2部分,并且有功和無功的變化規律并不是一定一致的,它們的變化會對系統狀態產生復雜影響。在選取負荷斷面時,需要全面考慮有功功率和無功功率的影響,因而必須解決對復功率進行聚類的難題。

現有的K-means聚類方法通常使用歐氏距離對樣本向量進行聚類,而定義在實數域的歐幾里德空間無法處理復功率向量。本文將K-means聚類方法中歐氏空間推廣到定義在復數域的酉空間,并定義了全節點負荷復向量的內積,進而給出全節點負荷復向量長度和距離的定義。這種方法應用于K-means聚類,可以直接處理復向量,更加準確地選取負荷斷面。實例表明,本文提出的基于全節點負荷向量聚類方法,對無功優化配置規劃問題可以做出更準確的計算。

1無功優化資產配置模型

配置無功補償裝置需要在節點電壓、網絡損耗和投資效益之間做平衡。在保證電壓水平的前提下,投資的費用小于降低網損獲得的收益,才是成功的投資,因此目標函數包含的3部分子目標全部轉化為費用來進行優化。

1.1目標函數

目標函數為:

minCT=CL+Cc+Cv

(1)

其中,CT為費用目標。系統有功網損費用為：

新裝補償電容器在服役期內年度等值費用為：

節點電壓偏差懲罰費用為：

其中,δr為全節點負荷斷面r在系統總運行時間T(通常以年為研究周期)內所占比例系數,共有L個斷面;Kd為系統有功電價;SG和SD分別為有功發電機與有功負荷節點集合;PGri和PLri分別為節點i在全節點負荷斷面r的有功出力與有功負荷;CB為補償電容器初始投資費用,包含購置費、安裝調試費等;CD為電容器壽命終止報廢后的殘值;CM為每年的維護費;ξ為利率;Y為電容器的壽命;Uri為節點i在全節點負荷斷面r下的電壓標么值;α為電壓偏差懲罰費用系數,對節點負荷統計分析后分段設定,系統共n個節點。

1.2約束條件

系統節點功率平衡方程為:

(2)

其中,Pi為節點i的注入有功功率;Qi為節點i的注入無功功率;Gij、Bij和θij分別為節點i和節點j之間的電導、電納和電壓相角差。

不等式約束為:

(3)

(4)

(5)

(6)

其中,Ui為節點i的電壓幅值;PGi為節點i發電機的有功出力；QRi為節點i無功源的無功出力;SG、SR、SL分別為發電機、無功源、聯絡線支路約束集合;Pij為系統節點i與節點j之間聯絡線的功率。為降低計算復雜度,無功補償裝置配置模型中不考慮電容器投切時間間隔約束。

2全節點負荷斷面聚類模型

電力負荷不但包括有功功率,還包括無功功率,通常用復功率來表示全節點負荷。合肥市翰林變電站某回出線24 h內的實測有功功率、無功功率和功率因數如圖1所示。

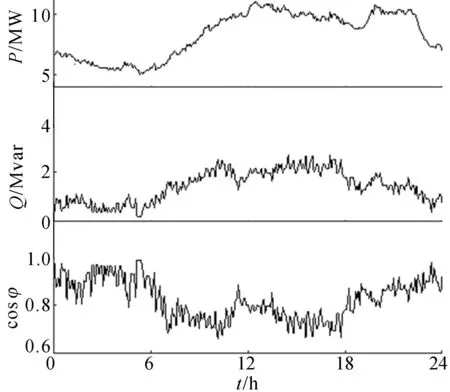
圖1　合肥市翰林變電站某回出線負荷曲線

從圖1可知,電網中有功功率和無功功率的變化并不一致,當節點中含有多種不同種類負荷時,這種不一致會更明顯。由電網實際負荷曲線可知,復功率雖然無物理意義,但包含了有功功率、無功功率、功率因數的全部信息,在用聚類方法選取負荷斷面時,復功率比僅用有功功率或無功功率能更準確地描述系統運行狀態。為了全面反映負荷在全年的變化過程,需要選取全節點負荷斷面，該斷面包含以下2層含義:① 系統的每個負荷點的形狀曲線都要考慮在內;② 每個負荷點的負荷都采用復功率的形式。

2.1全節點負荷向量的相似性度量

現有的K-means聚類方法所采用的歐氏距離只能對實向量的距離進行度量,無法處理復功率向量。為了在復數域上的線性空間引入度量概念,對于復數域中由m維負荷復向量構成的線性空間Cm,對?S1,S2∈Cm,S1={P11+jQ11，P12+jQ12，…，P1m+jQ1m}，S2={P21+jQ21，P22+jQ22，…，P2m+jQ2m},定義全節點負荷復向量的內積[10]為:

(7)

則Cm對此內積構成一個酉空間。酉空間Cm中負荷復向量S的長度可定義為:

(8)

從而可以定義酉空間Cm中負荷復向量S1和S2之間的距離為:

(9)

對?S1,S2,S3∈Cm,(9)式滿足距離函數的以下數學性質:

(1)d(S1，S2)≥0,兩向量之間的距離為非負數。

(2)d(S1,S1)=0,向量自身之間的距離為0。

(3)d(S1,S2)=d(S2,S1),向量之間的距離對稱。

(4)d(S1,S2)≤d(S1,S3)+d(S3,S2),向量之間的距離為三角不等式關系。

由此可知，(9)式可以對包含有功功率和無功功率的全節點負荷復向量進行相似性度量。

2.2K-means聚類個數的確定

利用K-means算法對全節點負荷復向量進行聚類,首先應確定負荷斷面的個數k[11]。步驟如下:

(1) 找出滿足經驗規則的負荷斷面聚類數目的最大值,經驗規則公式為:

(10)

其中,nY為初始負荷斷面的數目。

(2) 利用K-means算法計算由經驗規則確定的所有可能空間聚類。

(3) 分別計算步驟(2)得到的所有空間聚類的距離代價函數，公式為:

(11)

其中,M為全部負荷復向量的均值;Mr為類Cr所含樣本的均值;k為所要聚類的個數;S為類Cr內任一全節點負荷復向量。

(4) 距離代價函數最小的k為需要聚類的個數,即全節點負荷斷面的個數。

2.3全節點負荷復向量K-means聚類

負荷斷面K-means聚類的步驟如下:

(1) 令I=1,隨機選取k個負荷向量作為k個類簇的初始簇中心Mr(I),r=1,2,…,k。

(2) 計算每個負荷向量與這k個簇中心的距離d(Si，Mr(I)),其中,i=1,2,…,nY;r=1,2,…,k，如果滿足

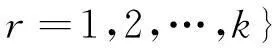
(12)

則Si∈Cr。

(3) 計算誤差平方和準則函數Jc。

(13)

其中，nr為類Cr中全節點負荷復向量的個數。

(4) 若|Jc(I)-Jc(I-1)|<ε則算法結束;否則I=I+1,重新計算k個新的聚類中心，即

(14)

(5) 返回步驟(2)。

得到負荷向量聚類結果后,聚類中心即為全節點負荷斷面,每個負荷斷面占總負荷的比例為:

(15)

3無功優化資產配置計算步驟

遺傳算法計算步驟如圖2所示。

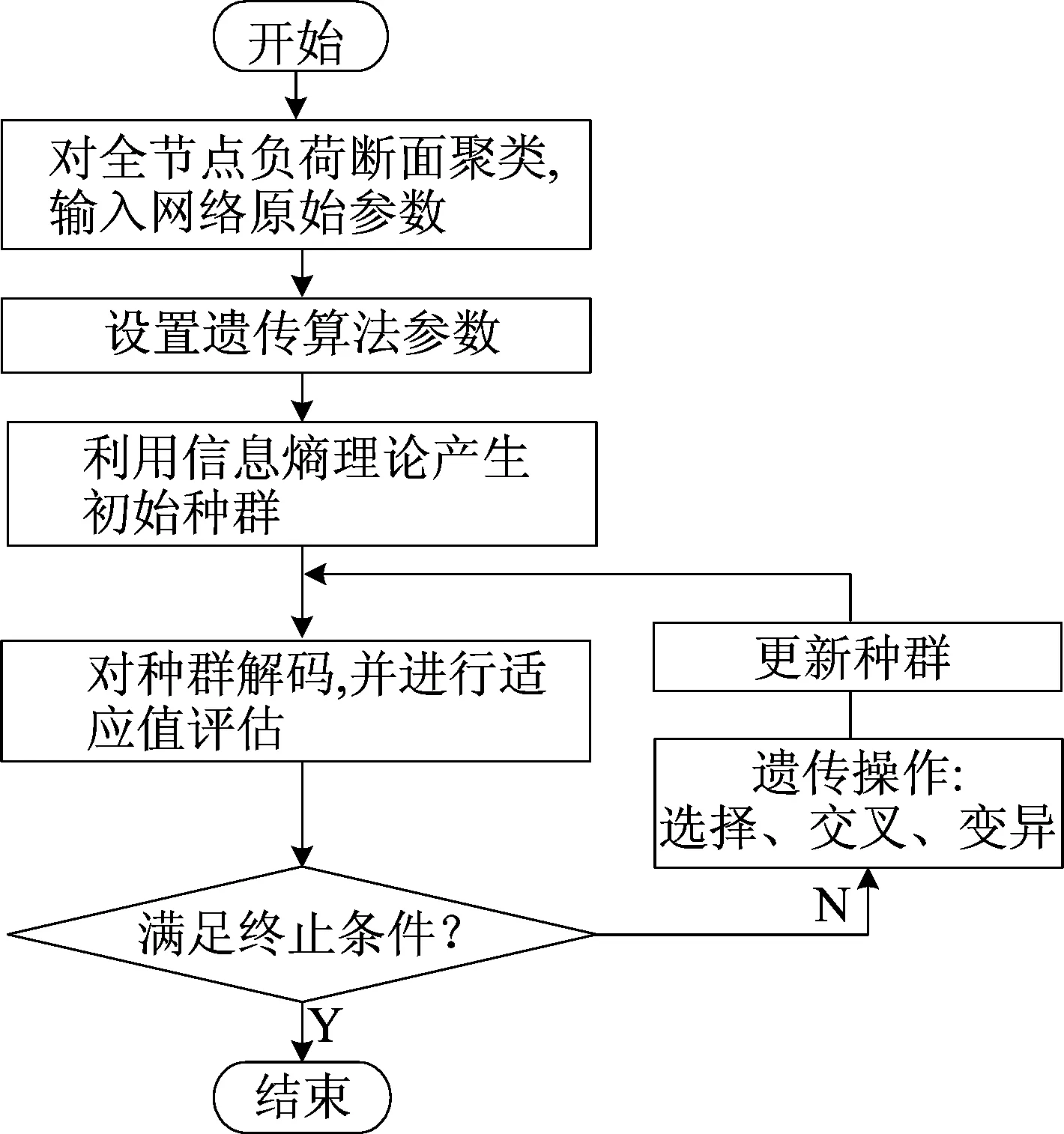
圖2　遺傳算法計算步驟

無功優化資產配置是典型的非線性混合非凸整數規劃問題[7],智能進化算法比較適合求解該類問題,本文選用遺傳算法求解。取無功補償電容器組投運組數為變量,假設可配置電容器的最大組數為N,則對系統中某個節點,其電容器投運組數的二進制編碼的長度為大于等于lb(N+1)的最小整數。例如,當可配置電容器的最大組數為7時,則二進制編碼的長度為lb(7+1)=3,對某節點來說,000代表不配置補償電容,001表示配置1組,010表示配置2組,依次類推。如果編碼中出現冗余編碼,則在實現程序過程中加入約束去掉冗余部分即可。給系統中每個節點進行二進制編碼,然后首尾相連作為參與遺傳算法的一個基因。

4算例分析

以PG&E69節點系統[12]為研究對象,該節點配電系統拓撲圖如圖3所示,該系統共有68條支路,基準電壓為12.66 kV,網絡總負荷為(3 802.19+j2 694.60)kV·A,分布在48個節點上。從實際電網中抽取48個負荷點的負荷曲線,經過歸一化變換后與PG&E69節點系統的48個負荷值相乘,得到48條包含有功功率和無功功率不同變化趨勢的負荷曲線。每條負荷曲線的長度為1 a,每天采樣12個點,共4 380個點。對全節點負荷復向量進行聚類,得到12個負荷斷面,利用wilks統計量[9]進行顯著性水平檢驗,結果表明12個負荷斷面差異明顯,分類有效。各斷面所占比例見表1所列,其中斷面1的負荷水平最高,斷面12的負荷水平最低。

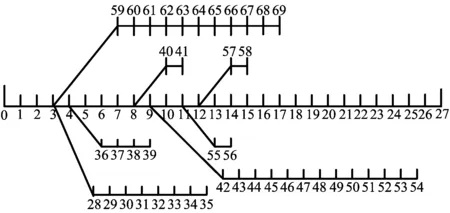
圖3　PG&E 69節點配電系統拓撲圖

每個節點可安裝的無功補償電容器的最大組數為15組,每組補償容量為1 kvar,年度等值費用假設為每組1 000元人民幣。每個節點無功補償配置的二進制編碼長度為大于等于lb(15+1)的最小整數,因此取4位二進制數作為節點基因編碼。對每個節點進行編碼,首尾相連組成遺傳算法的基因。系統有功電價為0.53元/(kW·h),電壓偏差懲罰費用系數為2 000元。利用遺傳算法求解無功補償優化模型,計算結果見表1所列,另外,表1還給出了每個負荷斷面所占比例以及此斷面下系統運行的有功損耗。

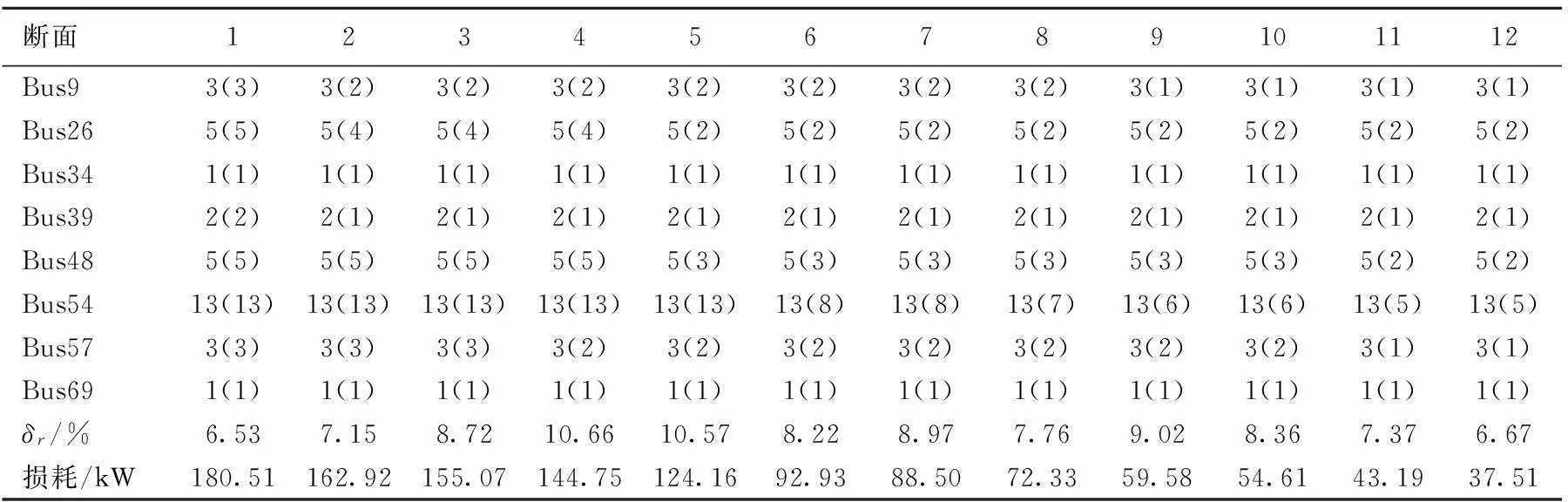
表1　PG&E 69系統無功優化資產配置結果

注：括號外數字表示節點安裝的電容器的組數；括號內數字為相應斷面下投入的電容器組數。

系統沒有安裝補償電容器之前在負荷斷面1下的有功網損為226.94 kW,補償后顯著降低到180.51 kW。在負荷斷面1所有的補償電容器全部投入運行,其他負荷斷面下,電容器根據網絡狀態做相應的調整。節點的電壓分布如圖4所示,由圖4可知，沒有安裝補償電容時,節點53、54的電壓標幺值為0.91左右,而安裝補償電容器后,電壓水平明顯改善,可以滿足10 kV等級電壓偏移±7%的要求。

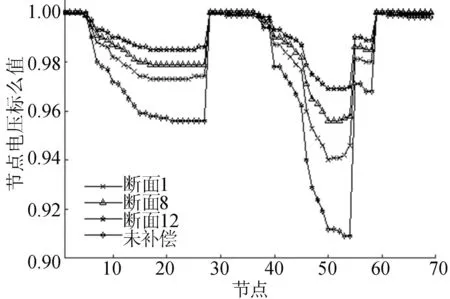
圖4　節點電壓分布

5結束語

在電網中配置無功補償裝置,既要滿足電壓運行的技術要求,還要滿足在有限投資下降低網損的經濟性要求。本文給出了考慮補償裝置年度等值費用、有功損耗費用和電壓偏差3個目標的無功優化模型。為了克服現有負荷斷面選取不準確可能導致模型計算誤差大的難題,本文將K-means聚類方法中歐氏空間推廣到定義在復數域的酉空間,給出了全節點負荷復向量長度和距離的定義,可以克服歐式距離只能度量實向量的缺點,實現直接對復功率負荷向量進行聚類的功能。算例表明,本文提出的方法能更好地實現無功優化資產配置。

[參考文獻]

[1]Dashti R，Afsharnia S. Decisions，Decisions:an asset management-based distribution system framework[J].IEEE Power and Energy Magazine，2014，12(3):96-108.

[2]龔莉莉,吳紅斌.基于ACPSO算法的含分布式電源配電網無功優化[J].合肥工業大學學報:自然科學版,2014,37(12):1441-1445.

[3]邢海軍,程浩忠,張逸.基于多種主動管理策略的配電網綜合無功優化[J].電網技術,2015,39(6):1504-1510.

[4]王成山,孫充勃,李鵬,等.基于SNOP的配電網運行優化及分析[J].電力系統自動化,2015,39(9):82-87.

[5]陳麗,侯晨偉,張晉國.基于全壽命周期成本的配電網多階段無功規劃[J].河北大學學報:自然科學版，2015，35(3):316-323.

[6]王佳賢,程浩忠,胡澤春.多負荷水平下的配電網無功優化規劃方法[J].電網技術，2008，32(19):56-61.

[7]何禹清,彭建春,毛麗林,等.含多個風電機組的配電網無功優化[J].電力系統自動化，2010，34(19):37-41.

[8]方延洪.考慮風電接入的配電網無功優化[J]. 合肥工業大學學報:自然科學版，2014，37(8):916-921.

[9]丁明,李生虎,洪梅.電力系統概率分析中的K均值聚類負荷模型[J].電力系統自動化，1999，23(19):51-54.

[10]丘維聲.高等代數[M].北京:科學出版社，2013:457-462.

[11]楊善林,李永森，胡笑旋,等.K-MEANS算法中的K值優化問題研究[J].系統工程理論與實踐，2006(2):97-101.

[12]劉健,畢鵬翔，董海鵬.復雜配電網簡化分析與優化[M].北京:中國電力出版社，2002:273-275.

(責任編輯閆杏麗)

Asset allocation of reactive power optimization based on complete bus load section clustering

GUI Qian-jin1,HUANG Hao2,ZHANG Da-bo3,KONG De-quan4

(1.Anqing Power Supply Company， State Grid Anhui Electric Power Company, Anqing 246003， China; 2.School of Electrical and Information Engineering， Anhui University of Technology， Ma’anshan 243032， China; 3.School of Electric Engineering and Automation， Hefei University of Technology, Hefei 230009， China; 4.Hefei Eaglory High-Tech Co., Ltd., Hefei 230088， China)

Abstract:A reactive power optimal asset allocation model is proposed， which considers the balance between the cost and benefit of the reactive power compensation device. The voltage target， the net loss target and the investment target are all converted into the cost in optimization. Aiming at the shortcomings of the load model in the existing optimization method， a method of the complete bus load section clustering is put forward. In this method，the Euclidean distance based on real vector is extended to the unitary space of the complex field. The method to measure the similarity between the complete bus load vectors and a detailed procedure for the complete bus load complex vector K-means clustering are given. The validity of the proposed model is verified by a numerical example based on the PG&E69 system.

Key words:complete bus load; complex power; clustering analysis; reactive power optimization; asset allocation

中圖分類號:TM714.1

文獻標識碼：A

文章編號：1003-5060(2016)03-0328-05

doi:10.3969/j.issn.1003-5060.2016.03.008

作者簡介：桂前進(1975-),男,安徽潛山人,國家電網安徽電力公司工程師.

基金項目：國家自然科學青年基金資助項目(51407056);中央高校基本科研業務費專項資金資助項目(2013HGXJ0623;2013HGBZ0184;2014HGQC0011)

收稿日期：2015-09-18；修回日期：2015-10-21