預應力混凝土箱梁剪力滯效應縱向影響長度分析

黃文雄，楊柳，王鵬，龔倩倩　(長江大學城市建設學院，湖北 荊州 434023)

譚利英　(荊州市城市規劃設計研究院，湖北 荊州 434000)

?

預應力混凝土箱梁剪力滯效應縱向影響長度分析

黃文雄，楊柳，王鵬，龔倩倩(長江大學城市建設學院，湖北 荊州 434023)

譚利英(荊州市城市規劃設計研究院，湖北 荊州 434000)

[摘要]為研究預應力混凝土箱梁剪力滯效應在縱向梁長方向上的影響長度，采用通用有限元分析軟件ANSYS，建立有限元分析模型，討論了剪力滯系數沿梁縱向分布規律，重點分析了寬跨比、跨高比、預應力大小以及集中荷載等參數對箱梁剪力滯效應縱向影響長度的影響。研究結果表明，無論箱梁頂板還是底板，其剪力滯系數最大值均在荷載施加的截面，遠離荷載施加的截面最大剪力滯系數迅速減小。荷載引起的剪力滯效應縱向影響長度較小，僅在荷載施加位置附近影響較大。隨著寬跨比增大，箱梁剪力滯效應縱向影響長度均越來越明顯，且越來越劇烈；跨高比的改變對箱梁頂板剪力滯效應影響較為劇烈，但其給箱梁造成的縱向影響不太明顯。 預應力以及集中荷載的改變對箱梁剪力滯效應影響較小，對箱梁剪力滯效應縱向影響長度的改變程度也較微弱。

[關鍵詞]橋梁工程；剪力滯效應；有限元分析；預應力；箱梁

箱形梁以其自身眾多優點不斷地運用于各種大型橋梁中，隨著箱梁的跨徑及截面尺寸不斷的加大，導致剪力滯效應越來越明顯。“剪力滯效應”的存在會使混凝土箱梁局部位置產生應力集中，甚至開裂，若忽略剪力滯的影響，就會低估箱梁結構實際產生的應力，從而造成結構的不安全。國內外專家學者對剪力滯效應有較多的研究：牛斌等對預應力混凝土寬箱梁剪力滯效應試驗研究，分析了荷載形式及結構參數對箱梁剪力滯效應的影響[1]；吳亞平等重點分析了荷載橫向變位下箱梁頂板與底板的剪力滯效應[2]；孫學先等研究了箱梁幾何參數對剪力滯效應影響[3]；藺鵬臻等人研究了翼板厚度變化對箱梁剪力滯效應的影響[4]。這些研究主要通過改變結構參數求得箱梁典型截面最大剪力滯系數，但忽略了該最大剪力滯系數沿箱梁縱向會有不同程度的降低。對于這種降低程度以及范圍，目前少有詳細的分析研究。考慮到工程實踐要具有安全性、經濟性和可靠性，因此有必要對此進行具體詳細的分析，以提高工程整體質量[5～7]。下面，筆者為分析箱梁典型截面最大剪力滯效應附近各截面最大剪力滯分布情況，運用大型通用有限元分析軟件ANSYS，以簡支箱梁為例，以集中荷載為外荷載施加對象[8,9]，著重分析箱梁跨中截面附近處各典型截面最大剪力滯效應，以探明預應力混凝土箱梁剪力滯效應沿箱梁縱向分布規律，并重點分析了常見結構參數[10,11]的改變對箱梁剪力滯效應縱向影響長度的改變程度，以更好的服務于工程實際。

1空間有限元分析模型的建立

1.1混凝土箱梁分析模型

筆者以有限元分析軟件ANSYS為平臺，建立參數化預應力混凝土箱梁簡支梁橋模型，模型長度為30m，有限元分析模型如圖1所示。

圖1　計算跨徑為30m的預應力混凝土箱梁模型

1.2荷載作用形式

分析的箱梁模型為簡支梁結構，外荷載以集中荷載作用形式施加。簡支梁跨中截面彎矩最大，得到的剪力滯效應最為明顯，因此，荷載分別施加到箱梁跨中截面腹板與頂板交界處的頂板上，具體施加情況如圖2所示。

1.3模型梁的計算結果分析

按照上述荷載形式施加一定大小的荷載，求解得到箱梁縱向正應力云圖，如圖3所示。運用有限元后處理手段提取所需要截面的各位置的應力(僅示跨中截面)，如圖4和圖5所示，進一步分析計算得出最大剪力滯系數。

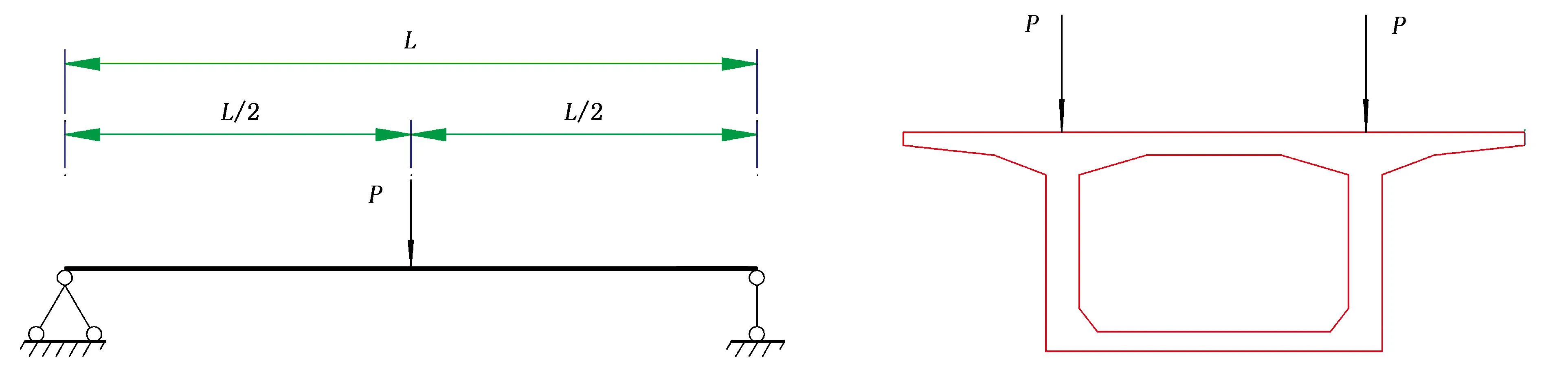
圖2　分析模型的荷載作用形式

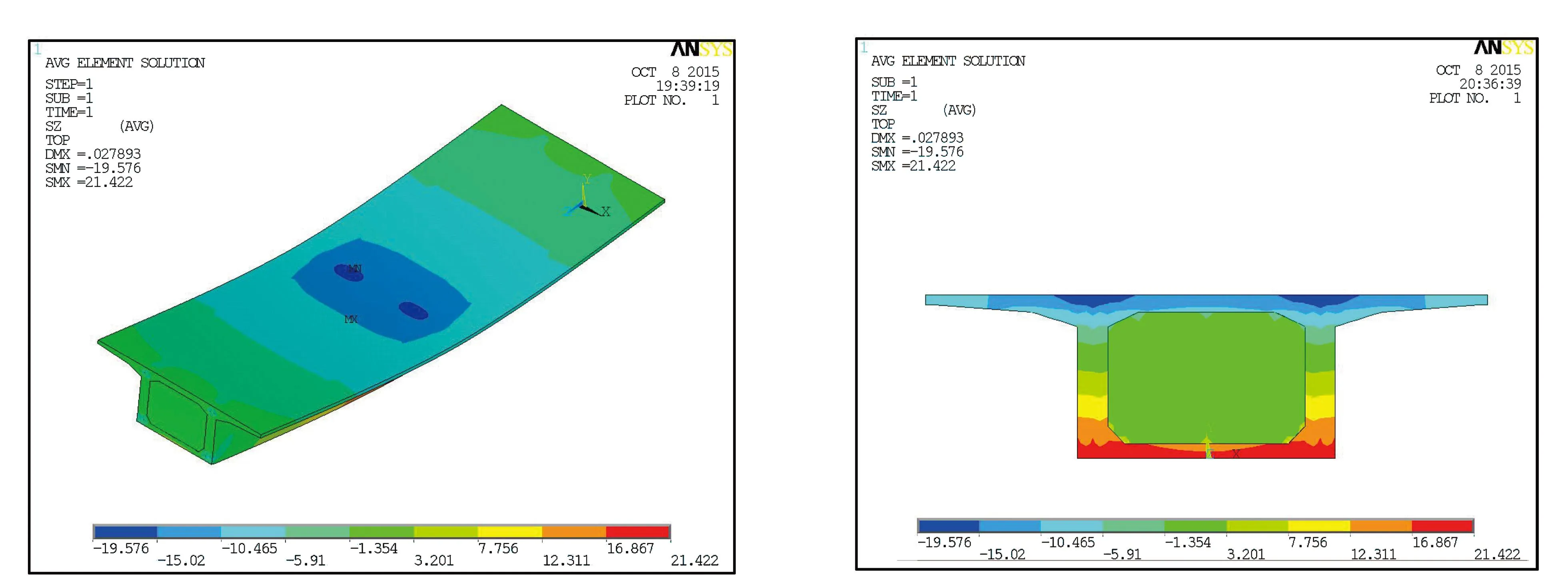
圖3　分析模型的縱向正應力云圖　　　　　　　　　　　　圖4　分析模型跨中截面縱向正應力云圖

通過對圖5的數據整理分析，得到該截面頂板的剪力滯系數分布圖，如圖6所示。由圖6可知，該截面最大剪力滯系數位于頂板與腹板交界處，最大值為1.426，最小值位于頂板邊緣，為0.732。

1.4剪力滯系數沿梁縱向分布規律

基于上述結果，沿梁縱向長度方向每間隔1m提取該截面剪力滯系數，將各截面最大剪力滯系數匯總，即可得到剪力滯系數沿梁縱向分布規律，圖7為分析模型各截面頂板最大剪力滯系數分布圖，圖8為分析模型各截面底板最大剪力滯系數分布圖。

由圖7、圖8可知，無論箱梁頂板還是底板，其剪力滯系數最大值均在荷載施加的截面，頂板最大值為1.426，底板最大值為1.103。遠離荷載施加的截面，最大剪力滯系數迅速減小，離荷載施加截面約1m的距離，最大剪力滯系數減小到1.07左右，減小約25.1%，該截面剪力滯效應已經相對比較微弱。另外，圖7、圖8在支座附近剪力滯系數有所增加，但是，由于簡支梁支座附近彎矩較小，研究剪力滯效應意義不大。因此，荷載引起的剪力滯效應縱向影響長度較小，僅在荷載施加位置附近影響較為明顯。

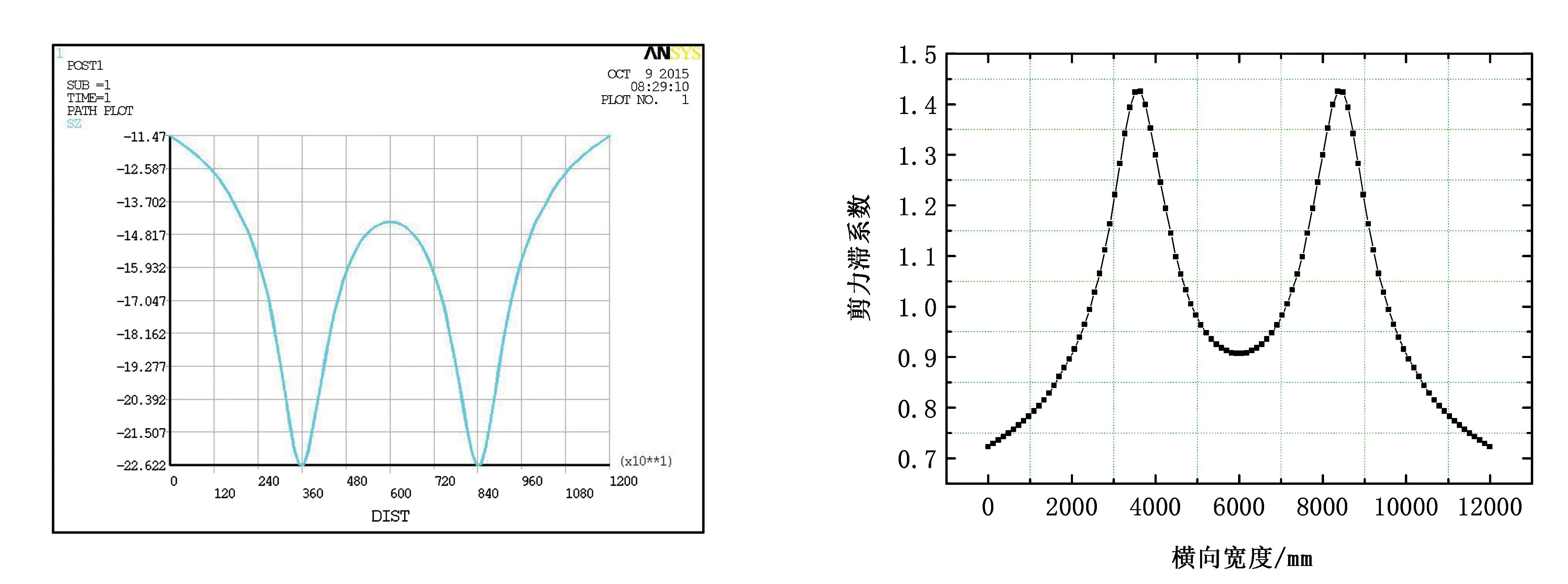
圖5　分析模型跨中截面頂板縱向正應力圖　　　　　　　　　圖6　分析模型跨中截面頂板剪力滯系數分布

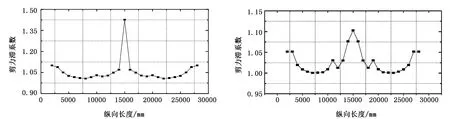
圖7　箱梁各典型截面頂板最大剪力滯系數分布　　　　　　圖8　箱梁各典型截面底板最大剪力滯系數分布

2剪力滯效應縱向影響長度分析

筆者主要研究集中荷載作用下箱梁的剪力滯效應，為探明剪力滯效應縱向影響長度，均取各截面頂板及底板最大剪力滯系數為代表值，研究剪力滯系數最大值的縱向分布規律，將重點分析荷載施加位置(即跨中截面)附近的最大剪力滯系數變化情況，通過改變寬跨比、跨高比、預應力大小和集中荷載大小等常見參數，以探明剪力滯效應沿箱梁縱向變化情況。

2.1寬跨比

保持箱梁長度30m不變，通過改變箱梁寬度，使箱梁寬跨比分別為0.2、0.4、0.6，保持其他參數不變，研究寬跨比的改變對箱梁剪力滯效應縱向影響長度的影響。圖9、圖10分別為各寬跨比下的頂板及底板最大剪力滯系數變化圖。

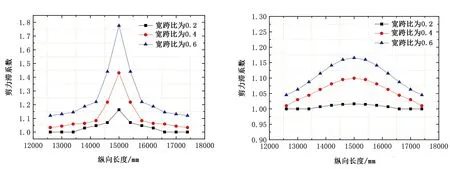
圖9　各寬跨比下頂板最大剪力滯系數沿梁長方向變化　　　　圖10　各寬跨比下底板最大剪力滯系數沿梁長方向變化

由圖9、圖10可知，隨著寬跨比的增大，無論是箱梁的頂板還是底板，同一截面處的剪力滯系數都隨之增大。當寬跨比由0.2增大到0.6時,箱梁頂板跨中截面剪力滯系數由1.16增大到1.78,增大了53.44%。在頂板跨中截面約1m范圍內剪力滯系數變化較快，圖9中曲線較為陡峭，1m范圍以外剪力滯系數變化較慢，曲線較為平坦。當寬跨比為0.2時，在距離荷載施加截面約0.4m時剪力滯效應就已經不太明顯，當寬跨比為0.4時，距離荷載施加截面約1.2m時剪力滯效應不太明顯,而寬跨比為0.6時，距離荷載施加截面約2.4m時剪力滯效應依然比較明顯。隨著寬跨比的增大，底板各截面處剪力滯系數均增大，剪力滯效應越來越明顯，縱向影響范圍越來越長。因此，隨著寬跨比增大，箱梁頂板及底板剪力滯效應縱向影響均越來越明顯。

2.2跨高比

保持箱梁長度為30m，分別設置梁高為2.5、3.75、7.5m，即考慮跨高比分別為12、8、4，研究跨高比的改變對箱梁剪力滯效應縱向影響長度的影響。圖11、圖12分別為各跨高比下的頂板及底板最大剪力滯系數變化圖。

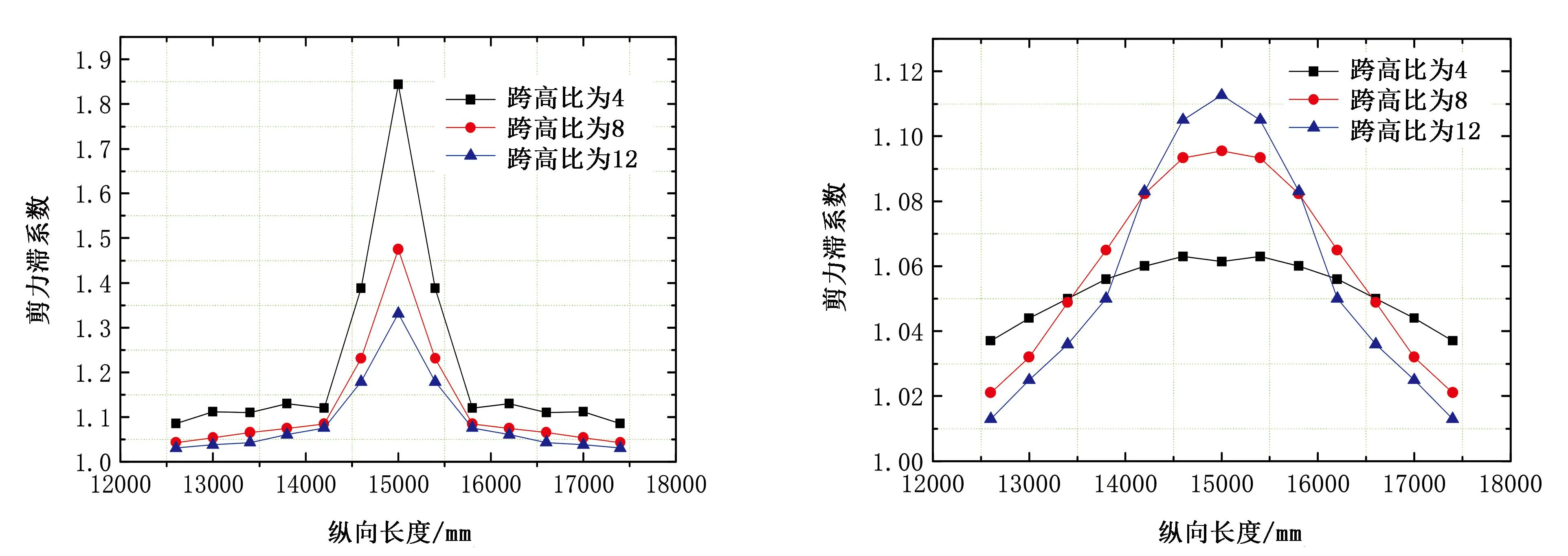
圖11　各跨高比下頂板最大剪力滯系數沿梁長方向變化　　　　圖12　各跨高比下底板最大剪力滯系數沿梁長方向變化

由圖11、圖12可知，對于箱梁頂板，隨著跨高比的增大，跨中截面剪力滯系數越來越小，跨高比由4增大到12，剪力滯系數由1.84減小到1.33，減小了27.71%。在距離跨中截面約0.8m范圍內，剪力滯效應變化較快，隨后均變化緩慢。無論跨高比多大，剪力滯后效應均在距離跨中截面0.8m處變的比較微弱，跨高比的改變對箱梁頂板剪力滯效應縱向影響不太明顯。對于箱梁底板，隨著跨高比的增大，跨中截面剪力滯系數越來越大，由1.06增大到1.11，相對比較微弱，但跨高比越小，剪力滯效應在縱向梁長方向變化越慢。跨高比越小跨中截面剪力滯系數也較小，但遠離跨中截面一段距離以后，反而較大，其縱向影響長度也較大。

2.3預應力大小

分別設置預應力大小為2.5、5、7.5kN，保持其他參數不變，研究預應力大小的改變對箱梁剪力滯效應縱向影響長度的影響。圖13、圖14分別為不同預應力作用下頂板及底板各截面最大剪力滯系數變化圖。

由圖13可知，改變預應力大小對箱梁頂板跨中截面剪力滯效應的影響較微弱，變化量在4.4%以內，其縱向影響長度也大致相同，均在距離跨中截面約0.8m處變的比較微弱，因此，預應力對箱梁頂板剪力滯效應縱向影響長度的改變程度較小。由圖14可知，隨著預應力的增大，底板各截面處剪力滯系數均增大，剪力滯效應越來越明顯，但均在距離跨中截面約2.4m處影響較小，因此，預應力對箱梁底板剪力滯效應縱向影響長度的改變程度較小。

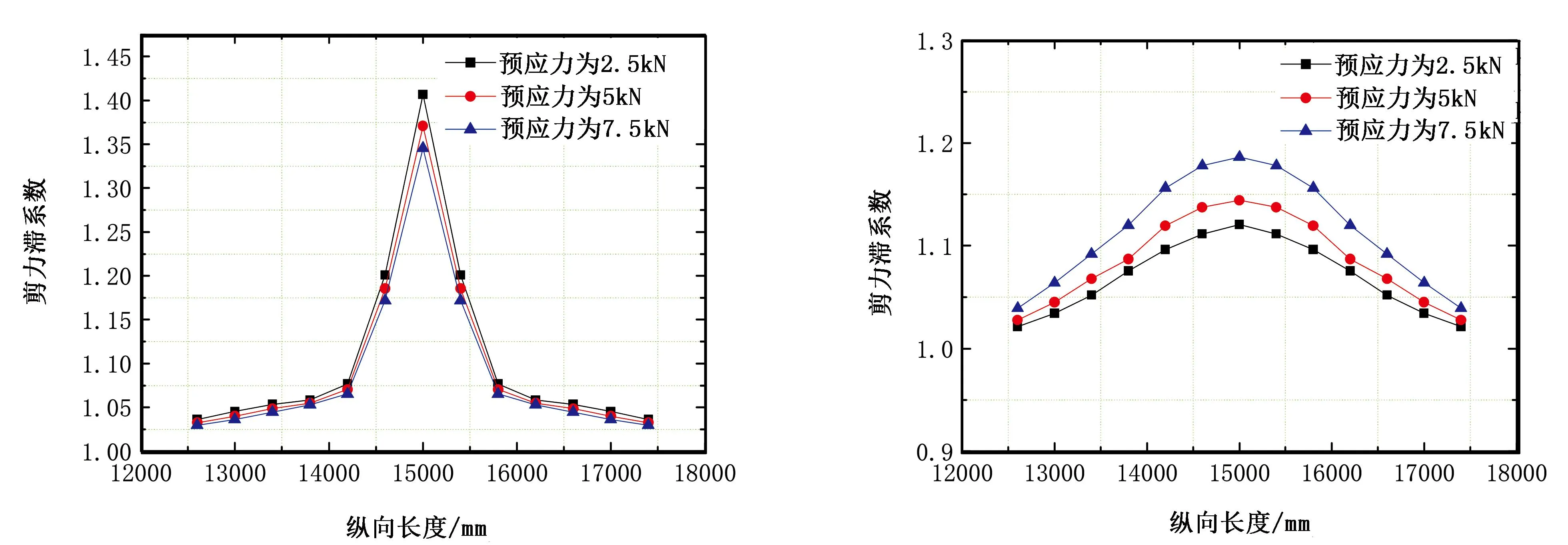
圖13　　　　不同預應力下頂板最大剪力滯系數沿梁　　　　　　　圖14　　　　不同預應力下底板最大剪力滯系數沿梁　　　長方向變化　　　長方向變化

2.4集中荷載大小

分別設置集中荷載大小為10、20、30kN，保持其他結構參數不變，研究集中荷載大小的改變對箱梁剪力滯效應縱向影響長度的影響。圖15、圖16分別為不同集中荷載作用下頂板及底板各截面最大剪力滯系數變化圖。

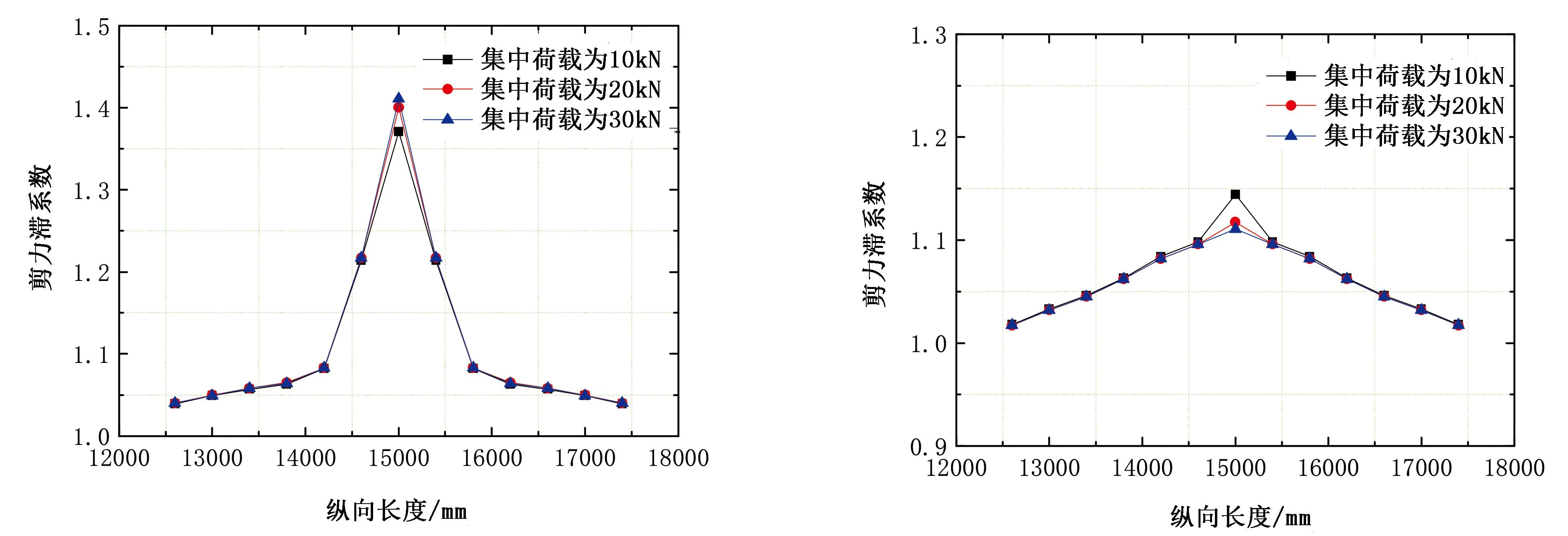
圖15　　　　不同集中荷在下頂板最大剪力滯系數沿梁　　　　　　圖16　　　　不同集中荷在下底板最大剪力滯系數沿梁　　　長方向變化　　　長方向變化

由圖15可知，集中荷載由10kN增大到30kN跨中截面剪力滯效應由1.37增大到1.41,增大了2.9%，距離跨中截面0.8m處剪力滯效應均變的較弱，且變化速率變得緩慢。由圖16可知，集中荷載由10kN增大到30kN跨中截面剪力滯效應由1.14減小到1.11，變化量在3%以內。距離跨中截面0.4m以外，3種情況下的剪力滯系數均大致處于同一直線上，變化較為微弱。因此集中荷載的改變對箱梁頂板以及底板的剪力滯效應影響較小，對箱梁剪力滯效應縱向影響長度的改變程度也較小。

3結論

通過有限元分析軟件ANSYS對箱梁模型的分析，可以得出以下幾點結論：

1)無論箱梁頂板還是底板，其剪力滯系數最大值均在荷載施加的截面，遠離荷載施加的截面最大剪力滯系數迅速減小。在支座附近剪力滯系數有所增加，但考慮到簡支梁支座附近彎矩較小，研究剪力滯效應意義不大。荷載引起的剪力滯效應縱向影響長度較小，僅在荷載施加位置附近影響較為強烈。

2)隨著寬跨比增大，箱梁頂板及底板剪力滯效應縱向影響均越來越明顯，且越來越劇烈，在工程實際中應適當降低寬跨比以降低寬跨比造成的剪力滯效應給橋梁帶來的不利影響。

3)跨高比的改變對箱梁頂板剪力滯效應影響較為明顯，但其給箱梁造成的縱向影響不太明顯；對于箱梁底板，隨著跨高比的增大，其縱向影響長度較大，但剪力滯效應均較小。

4)預應力對箱梁底板剪力滯效應縱向影響長度的改變程度較小。

5)集中荷載的改變對箱梁頂板以及底板的剪力滯效應影響較小，對箱梁剪力滯效應縱向影響長度的改變程度也較小。

[參考文獻]

[1]牛斌,楊夢蛟,馬林.預應力混凝土寬箱梁剪力滯效應試驗研究[J].中國鐵道科學,2004, 25(2):25～30.

[2]吳亞平,楊 玫,周大為,等.荷載橫向變位下箱梁頂板與底板的剪滯效應分析[J].土木工程學報，2007，40(10):8～12.

[3]孫學先,延力強,劉志峰.箱梁幾何參數變化對剪力滯效應的影響分析[J].水利與建筑工程學報，2009，7(1):29～31.

[4]藺鵬臻,楊子江,劉鳳奎,等.混凝土箱梁考慮翼板厚度變化的剪力滯效應[J].土木建筑與環境工 程,2013,35(1):76～79.

[5]項海帆.高等橋梁結構理論[M].北京：人民交通出版社，2002.

[6]吳文清.波形鋼腹板組合箱梁剪力滯效應問題研究[D].南京:東南大學，2002.

[7]馬磊，周林云，萬水.單箱三室波形鋼腹板箱梁剪力滯效應研究[J].中外公路，2013，33(3)：95～99.

[8]王新敏.ANSYS工程結構數值分析[M].北京：人民交通出版社，2007.

[9]黃文雄，譚利英.混凝土結構有限元分析中預應力筋模擬的新思考[J].中外公路.2013,33(2):108～111.

[10]牛斌,楊夢蛟,馬林.預應力混凝土寬箱梁剪力滯效應試驗研究[J].中國鐵道科學,2004,25(2)：25～30.

[11]黃文雄，譚利英.結構與材料參數變化對折線配筋先張梁局部應力的影響[J].公路交通科技.2012,29(1):75～79.

[編輯]計飛翔

[文獻標志碼]A

[文章編號]1673-1409(2016)04-0033-06

[中圖分類號]U398.9

[作者簡介]黃文雄(1980-)，男，博士，副教授，現主要從事現代橋式及橋梁結構設計理論方面的教學與研究工作;E-mail:84583318@qq.com。

[基金項目]國家自然科學基金項目(51408057);國家大學生創新創業訓練計劃項目(104892014002)。

[收稿日期]2015-11-28

[引著格式]黃文雄，楊柳，王鵬，等.預應力混凝土箱梁剪力滯效應縱向影響長度分析[J].長江大學學報(自科版)，2016,13(4)：33～38.