談陀螺定向在獨立坐標系中的應用

劉坤，張杰勝

（中鐵四局集團，安徽 合肥 230041）

談陀螺定向在獨立坐標系中的應用

劉坤，張杰勝

（中鐵四局集團，安徽 合肥 230041）

在地下工程洞內導線測量中，加測陀螺定向邊是消除角度誤差的積累。在工程獨立坐標系下，地面已知邊精度已經確定、陀螺儀已經選定、作業人員已經固定情況下，文章提出了合理地選取地面已知邊以減小△的影響，采用合理的計算方法提高γ的計算精度，既方便外業操作又簡化了內業計算，保障了陀螺定向工作的可靠性。

陀螺定向；儀器常數；子午線收斂角；獨立坐標系

1 概述

在地下工程洞內導線測量中，受到測角誤差和起始方位角誤差的影響，隨著導線節點的增加，點位的橫向誤差也在逐步地積累，導線的終點表現得更為明顯[1]。為了解決導線測量引起的方向誤差積累，通常加測陀螺定向[2]，校核導線測量中的測角誤差，并將其作為已知條件參與導線測量平差，以提高導線的精度，減小貫通誤差。

陀螺定向的北方向是陀螺北方向，其方向與真北方向有個常數差△。真北方向與坐標北方向之間也存在著一個夾角，稱作子午線收斂角。三者之間的夾角又稱作三北方向改正角[3]。

2 影響待定邊方位角精度的因素

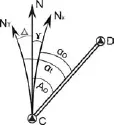
圖1 三北方向示意圖

如圖1所示，N為真北方向，NT為陀螺北方向，Nx是坐標北方向。陀螺北方向NT與真北方向之間的夾角，稱為儀器常數，用△表示。陀螺子午線位于地理子午線以東△為正，反之為負。真北方向N與坐標北方向Nx之間的夾角稱為子午線收斂角，用γ表示，其符號由安置儀器的位置確定，在中央子午線以東為正，以西為負。圖中精密導線邊CD的坐標方位角為α0，子午線收斂角為γ，αt為其陀螺方位角。在實際工作中，真北方向角A0是未知的，需要求解。C點為儀器設站點，那么有：

由（1）、（2）可得：

儀器常數△的誤差包括了已知邊坐標方位角的誤差、儀器操作誤差以及外部環境的影響。

在地鐵陀螺定向工作中，需要用地面已知求解△來計算地下待定邊的坐標方位角。這里地下待定邊的坐標方位角用αt下表示，儀器常數用Δ′表示，子午線收斂角用γ下表示，那么有：

根據誤差傳播定律可得：

除去地面控制網的測角誤差之外，定向邊坐標方位角的精度，取決于定向邊陀螺定向精度、儀器常數和子午線收斂角三個方面的因素。在實際工作中，在已知邊上測定儀器常數以及在定向邊上測定陀螺方位角，陀螺定向測量的中誤差mt可認為是定值。在已知點坐標精度固定的情況下，要提高待定邊坐標方位角的定向精度，主要從儀器常數△和子午線收斂角γ兩方面進行分析。

3 儀器常數的適用范圍

在（3）和（4）式中，對于地下待定邊的儀器常數，文中給出了不同于地面已知邊測定的儀器常數的表示方法，兩條邊上測量的常數值是否相等。傳統觀念中都是認為常數值是等值代換，將式(3)的值直接可以代入（4）式中進行計算，限定條件是測定儀器常數的已知邊宜與地下定向邊的平面位置盡量接近[4]，沒有量化標準。要提高陀螺定向的精度，這直接關系到已知邊位置的選擇[5]。

在精密導線控制網中，選定一條邊作為基準邊，與這條邊不同的距離和方向上分組選擇導線邊作為驗證邊，在選擇的所有導線邊上都進行陀螺定向測量，并記錄相應的氣象條件，求算各條邊上儀器常數，然后進行不同距離和不同角度的邊上與已知邊的測定的儀器常數統計分析，總結有如下規律：

①已知邊與定向邊之間的距離小于2000m時，儀器常數比較穩定。超出這個范圍，儀器常數會有較大的變化。

②已知邊與定向邊的相對方位的不同對儀器常數產生的影響較小。

③已知邊與待定邊的測量環境溫差要控制在10℃之內。

4 子午線收斂角的計算精度

子午線收斂角可由大地坐標（B，l）計算，也可以由平面坐標（x，y）計算，在《控制測量學》[6]給出了相應的計算公式：

式中：l為測站到中央子午線的經差；B為測站緯度；t=tanB；；η=e′cos2B；e為第一偏心率，e′為第二偏心率。

（6）、（7）兩個公式計算精度高，由于計算量大，在實際工作中常采用簡化公式，計算量小且計算精度滿足規范精度的要求[7]。

上述的子午線收斂角計算公式，平面坐標（x，y）均為相對于中央子午線投影后得到的自然坐標，而在工程施工中常采用的是獨立坐標系的坐標，計算時注意加以區分。在計算工程施工的獨立坐標系的子午線收斂角時，首先要根據投影自然坐標與獨立坐標之間的坐標轉換參數關系，將獨立坐標恢復為自然坐標再代入公式進行計算。

在無轉換參數和無法確定γ的正負號的情況下，無法直接使用上述公式，可按以下方法解決。

當已知邊和待定邊距離較近，滿足前述的要求時，可認為Δ=Δ′，將（3）式代入（4）式，有：

角可以從電子地圖上查出，ρ和Nf取常數值，代入（9）式可得：

將（11）代入（10），有：

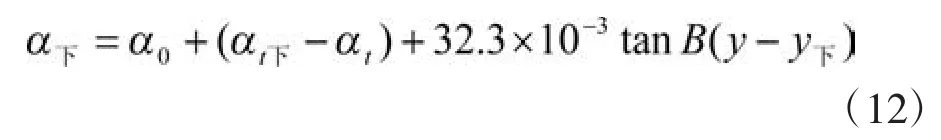
式中收斂角是計算兩者的差值，無論是獨立坐標或是自然坐標，兩點之間的坐標值之差是相同的，且收斂角的正負號取決于設站點y坐標差，這樣就無需進行坐標轉換和設站點位置判斷了。

5 實例驗證

成都軌道交通7號6標線流科區間控制網，設計提供了控制網的獨立坐標系的坐標，如表1所示。這里我們將GPS023→KAN1這條邊作為地面已知邊，將邊ZTL775→Z682和邊YTL505→Y570作為待定邊，地圖上查得測區緯度310。經過陀螺定向和計算后得到待定邊的坐標方位角，將之與控制網已知坐標方位角進行比較，看較差是否滿足規范要求，用于驗證測量及計算方法的可靠性。控制點坐標見表1，導線邊位置示意圖見圖2。

控制網坐標 表1

圖2 導線邊位置示意圖

①陀螺定向觀測

基準邊陀螺方位角測量精度評定 表2

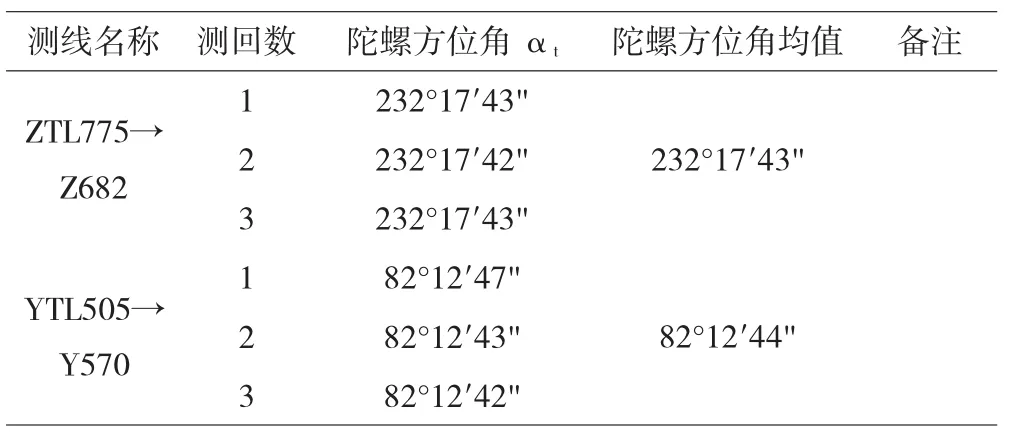
檢核邊陀螺觀測計算表 表3

②待定邊方位角計算

將數據代入（12）式可得：

檢核邊ZTL775→Z682方位角：

檢核邊YTL505→Y570方位角：

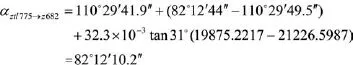
③坐標方位角檢核

坐標方位角較差 表4

6 結論

本文研究了陀螺定向工作中已知邊和待定邊的位置關系對儀器常數的影響，提供施工現場在陀螺定向已知邊位置選取的參考依據；在獨立坐標系控制網下的陀螺定向工作中，在未知自然坐標轉換參數的情況下，通過公式原理的推導方便地解算出子午線收斂角，并通過坐標差值的正負取代了關于設站位置相對于中央子午線位置的正負號判斷，合理方便地解決了類似工程項目在陀螺定向工作中存在的問題。

[1]謝平，劉元志.陀螺全站儀在礦山測量方面的運用[J].國土資源導刊，2013（5）：92-95.

[2]尹志強，盛劍，張秋芳.陀螺全站儀在地鐵聯系測量中的應用[J].測繪與地理空間信息，2012（S1）：123-124.

[3]張正祿.工程測量學[M].武漢：武漢大學出版社，2005.

[4]GB50308-2008，城市軌道交通工程測量規范[S].

[5]胡榮明.陀螺定向時已知邊位置的選擇 [J].西安科技大學學報，2007（6）：260-262.

[6]孔祥元，郭際明.控制測量學[M].武漢：武漢大學出版社，2009.

[7]鄔熙娟，江國焰，高俊強.子午線收斂角計算公式及其計算精度的分析[J].現代測繪，2005（12）：22-25.

TU198+.6

B

1007-7359（2016）06-0170-03

10.16330/j.cnki.1007-7359.2016.06.066

劉坤（1978-），男，畢業于武漢大學，碩士；高級工程師。研究方向：精密工程測量。