關于緊算子的若干探討

林梅羽林群雄(.莆田學院基礎教育學院 福建 莆田 3500；.莆田第二中學 福建 莆田 3500)

關于緊算子的若干探討

林梅羽1林群雄2
(1.莆田學院基礎教育學院 福建 莆田 351100；2.莆田第二中學 福建 莆田 351100)

給出嚴格奇異空間及嚴格余奇異空間上算子T是緊的充分必要條件，證明了對任意復無限維的Hilbert空間H，有K(H)=I(H)成立，并給出對于Banach空間X，使K(X)=I(X)不成立的一個反例。

緊算子；非本性算子；嚴格奇異算子；嚴格余奇異算子

1.引言及定義

眾所周知，任意無窮維Hilbert空間H上的一個（有界線性）算子T是緊算子當且僅當其值域R(T)不含無窮維閉子空間。R.G.Douglas在文獻[1，P23]中提出這樣的問題：當Hilbert空間用任意的Banach空間代替時，上述命題是否仍然成立？D.Van Dulst在文獻[4]中否定回答了R.G.Douglas的上述問題，亦即有Banach空間X，其上存在一算子T，使R（T）含有X的無窮維閉子空間，但T不是緊算子。文章主要討論一類特殊Banach空間上算子T是緊的充要條件，證明了在Hilbert空間上，緊算子和非本性算子是一致的，并給出上述命題對Banach空間不成立的例子。

如無特別聲明，文章始終設H，K為復無限維的Hilbert空間，X，Y為復無限維的Banach空間，X*，Y*分別表示X，Y的共軛空間，B（X，Y），K（X，Y）分別表示由X到Y的有界線性算子的全體，緊算子的全體。當X=Y時，其分別簡記B（X），K（X）。設T∈B（X），M是X的閉子空間，T*表示T的伴隨算子，T｜M表示T在M上的限制，N(T)和R(T)分別表示T的零空間和值域。α(T):=dimN(T)表示零維，β(T):=dimY/R(T)表示虧維。稱T∈B（X）為Fredholm算子，若α(T)＜∞，且β(T)＜∞。X上Fredholm算子的全體記為Φ(X)。稱T∈B（X）為非本性算子，若對任給的算子A∈B（X），有I-TAΦ(X)，等價地，對任給的算子A∈B（X），有IAT∈Φ(X)。X上非本性算子的全體記為I（X）。稱T∈B（X）是嚴格奇異算子，若對于X的某個閉子空間M，T｜M是M到T（M）上的同構，則M必是有限維的。X上嚴格奇異算子的全體記為S（X）。稱T∈B（X）是嚴格余奇異算子，若對于X的某個閉子空間M，QXMT是滿射，則X/M必是有限維的，其中QXM是X到X/M上的自然滿射。X上嚴格余奇異算子的全體記為SC（X）。以上概念見于文獻[5，6]，下面給出文章所需要的有關概念。

定義1.1（1）稱Banach空間X是嚴格奇異空間，如果S(X)=K(X)。

（2）稱Banach空間X是嚴格余奇異空間，如果SC(X)=K(X)。

（3）稱Banach空間X是非本性空間，如果I(X)=K(X)。

顯然，由K(X)?S(X)?I(X)及K(X)?SC(X)?I(X)，易知I(X)=K(X)?S(X)=I(X)和I(X)=K(X)?SC(X)=I(X).

定義1.2（1）稱X和Y具有嚴格奇異關系，如果S(X，Y)=K(X，Y)，簡記為。

（2）稱X和Y具有嚴格余奇異關系，如果SC(X，Y)=K(X， Y)，簡記為。

（3）稱X和Y具有非本性關系，如果I(X，Y)=K(X，Y)，簡記為。

然而，由文獻[3]的命題2.c.3知，B(co,lp)=K(co,lp),B(lq,l1)=K(lq,l1)，故I(co,lp)=S(co,lp)=K(co,lp),I(lq,l1)=SC(lq,l1)=K(lq,l1)。

這說明嚴格奇異關系，嚴格余奇異關系，以及非本性關系皆不具備自反性，更不是等價關系。

2.主要結果

定理2.1設Banach空間X是嚴格奇異空間，則T∈B（X）當且僅當R(T)不含無窮維閉子空間。

證明：充分性。設R(T)不含無窮維閉子空間，則T∈B（X），又X是嚴格奇異的，因此T∈B（X）。

例2.2 Spiros A.Argyros等在文獻[7]中構造了一個H.I.空間XK，其上的有界線性算子的全體B (XK)=｛λI+K:λ∈￡,K∈K(XK)｝，從而證實了Pisier G.在20世紀80年代提出的猜想：存在一個無限維的Banach空間X，使得B(X)=｛λI+K:λ∈￡,K∈K(X)｝，對于空間XK，有：

推論2.1設X是非本性空間，則T∈K（X）當且僅當R(T)不含無窮維閉子空間。

例2.1設X=co或lp(1≤p＜∞)，易知K(X)是B(X)中唯一的非平凡閉雙側理想（見[5]的推論5.4.23），因此co,lp(1≤p＜∞)都是非本性空間。

（1）XK是非本性空間，即K(XK)=I(XK)。

（2）T∈K(XK)當且僅當R(T)不含無窮維閉子空間。

證明：（1）若T∈I(XK),T=λI+K其中λ∈￡,K∈K(XK)，則必有λ=0，從而T=K∈K(XK)。事實上，如若λ≠0，取S=λI∈Φ(XK)，于是有K=S+ T∈Φ(XK)矛盾。因此I(XK)=K(XK)。

（2）由（1）及推論2.1知（2）顯然成立。

眾所熟知，可分Hilbert空間同構于l2空間。因此，由例2.1知可分Hilbert空間是非本性空間。對于不可分的情況，我們有：

定理2.2任意的Hilbert空間H都是非本性空間。

證明：設T∈I(H)K(H)，由已知事實“Hilbert空間H上的算子T是緊的當且僅當其值域R(T)不含無限維閉子空間”（見[1]），存在R(T)的無窮維閉子空間M。由T的連續性知，N:T-1(M)是H的無窮維閉子空間。因此T1:=T｜N:N→M是滿射的連續線性算子，即T1∈B(N,M)。又T1:=N (T1)⊕(N(T1))⊥→M，從而T2：=:T1｜N(T1)：(N(T1))⊥→M是有界可逆算子。定義算子A：

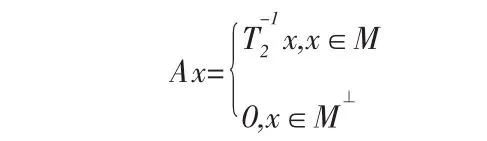
顯然，A∈B(H)，且對?x∈M，有(I-TA)x=0，即M?R(T)，從而α(ITA)=∞，這與T∈I（H）矛盾。

例2.1和例2.2說明存在不與Hilbert空間同構的Banach空間X，其上的非本性算子和緊算子是一致，亦即定理2.2成立。而下面的例2.3將說明定理2.2并非對一切的Banach空間都成立。

例2.3設Z:=lp⊕lq,1≤p＜q＜∞，Z上的范數取為：‖(x,y)‖=‖x‖p+‖y‖q,?(x,y)∈lp⊕lq，則Z不滿足定理2.2，亦即Z不是非本性空間。事實上:

由算子V及U的定義知，V:lp→lq是恒同映射，U:lp→lq是單射，所以T是單射。又U=是有限秩算子，其中，為en的系數泛函，n=1,2,….所以U是緊算子。由lp和lq是完全不可比空間（見[3，P75]），因此V∈S(lp,lq),U∈S(lq,lp)，故T=JlpUPlq+JlqVPlp∈S(Z)，其中Jlp(Jlq)表示由lp(lq)到Z=lp⊕lq的嵌入映射，Plq(Plp)表示Z=lp⊕lq到lq(lp)上的投影算子。

作為定理2.1某種形式上的對偶命題，我們有：

定理2.3設X是嚴格余奇異空間，則T∈K（X）當且僅當R(T*)不含無窮維閉子空間。

證明：必要性。設T∈K（X），則T*∈K(X*)，由定理2.1，R(T*)不含無限維閉子空間。

充分性。若R(T*)不含無限維閉子空間，則T*∈K(X*)，因此T∈SC（X）=K(X)。

下面的例子說明定理2.3的條件“X是嚴格余奇異空間”是不可缺少的。

例2.4設Z:=lp⊕lq,2≤p＜q≤∞，Z上的范數取為：‖(x,y)‖=‖x‖p+ ‖y‖q,?(x,y)∈lp⊕lq，算子T取為例2.3的定義的算子，則由例2.3知，T∈S（Z）K(Z)，且R(T)不含無限維閉子空間（若不然，設M是R(T)的無限維閉子空間，記N:=T-1M，由T的線性性及連續性知，N是Z的無限維閉子空間，又T是單射，所以T｜N是N到M上的一個同構，這與T∈S（Z）矛盾）。又Z是自反的，所以存在空間X，及算子S∈B（X），使得X*=Z,S*=T，所以R(S*)=R(T)不含無限維閉子空間，又T?K(Z)，所以S?K(X)。這說明，若X不是嚴格余奇異空間，亦即SC(X)≠K(X)，則定理2.3不成立。

推論2.2設X是非本性空間，則T∈K（S）當且僅當R(T*)不含無限維閉子空間。

命題2.1（1）設X是自反的，嚴格余奇異空間，X*是次投影的，則T∈K（X）當且僅當R(T)不含無限維閉子空間。

（2）設X是超投影的，嚴格余奇異空間，則T∈K（X）當且僅當R (T*)不含無限維閉子空間。

證明：（1）若R(T*)不含無限維閉子空間，則T∈S（X），由X自反，故T*∈SC（X*），又X*是次投影的，由文獻[6]的命題3.2.26可得，T∈SC （X）=K(X)。必要性顯然。

（2）設R(T*)不含無限維閉子空間，則T∈S（X），又X是超投影的，由文獻[6]的命題3.2.27可得，T*∈S（X*），從而T∈SC（X）=K(X)。必要性顯然。

3.相關結果的推廣

作為單個Banach空間X的推廣，我們有如下結論：

證明：（1）若R(T*)不含無限維閉子空間，則T∈S（X,Y）=K(X,Y)。

（2）若R(T*)不含無限維閉子空間，則T*∈S（Y*,X*），從而T∈SC （X,Y）=K(X,Y)。

引理3.1[8]（1）設Y是次投影的，則I（X,Y）=S(X,Y)。

（2）設X是超投影的，則I（X,Y）=SC(X,Y)。

（2）X→sc

Y，X是超投影空間，則T∈K（X,Y）當且僅當R(T*)不含無限維閉子空間。

證明：（1）由定理3.1及非本性空間的定義知（1）成立。

（2）若R(T*)不含無限維閉子空間，則T∈S（X,Y）?I(X,Y)，又X是超投影的，由引理3.1知，I（X,Y）=SC(X,Y)，所以T∈SC（X,Y）=K(X,Y)。

命題3.1設T∈I（X,Y），若T在X的某個無限維閉子空間M上的限制T｜M:M→Y同構，則M不含X的可補的無限維閉子空間。

證明：若不然，則存在X的無限維可補閉子空間N，且N?M。設PN:X→Y是X到N上的連續投影，顯然P=(T｜M)-1TP，又T∈I（X,Y），所以P∈I（X），顯然N?ker(I-P)，故α(I-P)=∞，這與P∈I（X）矛盾。

定理3.2設X是次投影空間，則I（X,Y）=S(X,Y)。

證明：若T∈I（X,Y）S(X,Y)，則有X的無限維閉子空間，使得T｜M:M→Y是同構嵌入，又X是次投影，所以有X的無限維可補閉子空間N，N?M，這與命題3.1矛盾。

［1］DouglasRG.BanachAlgebraTechnique in Operator Theory[M].AcademicPress,1972.

［2］Aiena P.Fredholm and Local Spectral Theory,With Application to Multipliers [M].Dordrecht:Kluwer Acad Publishers,2004.

［3］Lindenstrauss J,Tzafriri L.Classical Banach spaces I[J].springer-Verlag,1977.

［4］Van Dulst D.關于R.G.Douglas的一個問題[J].華東師范大學學報：自然科學版，1988，02：1-2.

［5］Caradus S R,Pfaffenberger W E,Berteam Yood.Calkin Algebras and Algebras of Operators on Banach Spaces[M].New York:Marel Dekker,1974.

［6］鐘懷杰.Banach空間結構和算子理想[M].北京：科學出版社，2005.

［7］Spiros A Argyros,Richard G Haydon.A Hereditarily Indecomposable L∞-Space thatsolvetheScalar-plus-compactProblem[EB/OL].http://arXiv.org/abs/0903.3921v2, 2009.

［8］Aiena P,Gonazalez M.Essentially incomparable Banach space and Fredholm Theory[J].Pro Roy Irish Acad,1993,93A(01):49-59.

Notes on Compact Operators

Lin Mei-yu1Lin Qun-xiong2
(1.College of Basic Education,Putian University Fujian Putian 351100；2.The NO.2Middle School of Fujian PuTian city Fujian Putian 351100)

Gives the necessary and sufficient condition for T is compact operator on strictly singular spaces or strictly cosingular spaces,proves that K(H)=I(H)for any Hilbert space H,and gives a counter-example on Banach space X where K(X)=I(X)does not hold.

Compact operator;Inessential operator;Strictly singular operator;Strictly cosingular operator

O177.2

A

2095-7327（2016）-04-0148-03

林梅羽（1959—），男，漢族，福建莆田人，高級講師，主要從事基礎數學研究。

林群雄（1984—），男，漢族，福建莆田人，中學二級教師，主要從事中學數學教學研究及空間與算子結構理論研究。