數列極限求解方法的探討

張俊青（山西職業技術學院 山西 太原 030006）

數列極限求解方法的探討

張俊青
（山西職業技術學院 山西 太原 030006）

數列是數學中一個非常基礎的概念，在高等數學中有非常重要的應用。數列極限的計算，是微積分學習中的一個難點，本文通過實例對多種求極限的方法進行了有益的探討。

數列極限；求解方法

0.引言

數列極限是一個非常重要的數學概念，本文重點介紹了數列極限的求解方法。包括單調有界法，“求”與“證”結合法，ε-N定義法等。通過實例本文總結了這些方法的特點、適用范圍以及需要注意的問題。

1.單調有界法

證明：an=,易見數列an｛｝是遞增的，現用數學歸納法證明an｛｝有上界。顯然a1=，假設an<2,則有an+1==2，從而a

n+1<2,即可知數列an｛｝有上界。根據單調有界定理可得，數列an｛｝有極限。假設=a。

求解可得a=2或a=-1，因a＞0，固取a=2

2.“求”與“證”結合

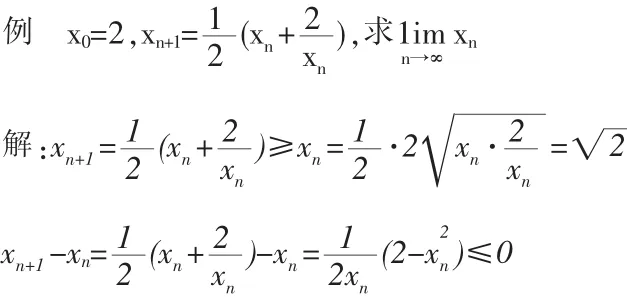
∴數列xn｛｝是單調遞減且有下界的數列。所以，xn｛｝必有極限。以下求xn｛｝的極限，設

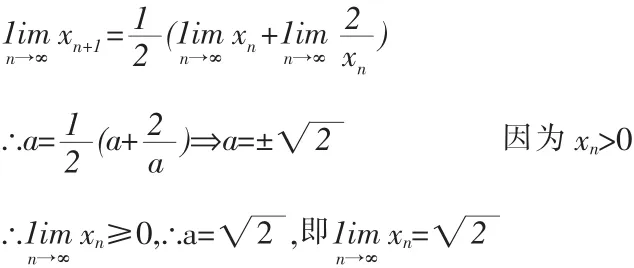
注意：對于極限存在性的證明是必須的，只做求解而不做證明很可能導致錯誤的結果。不妨來看這樣一個反例：xn=5·2n-1(n=1,2,···)，則xn+1=xn·2(*)。

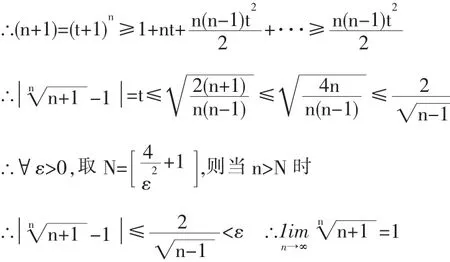
用數列極限定義法求解時，關鍵是找數列極限定義中的正整數N。

4.相應子序列的極限與函數極限等值

將數列中的n換成x，將數列的極限轉化為相應函數的極限，求出此函數的極限，則得到相應數列的極限。

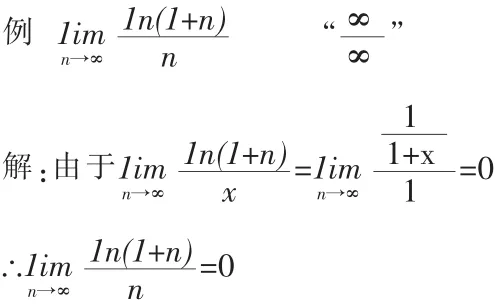
5.級數斂審法

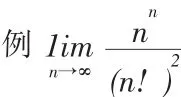
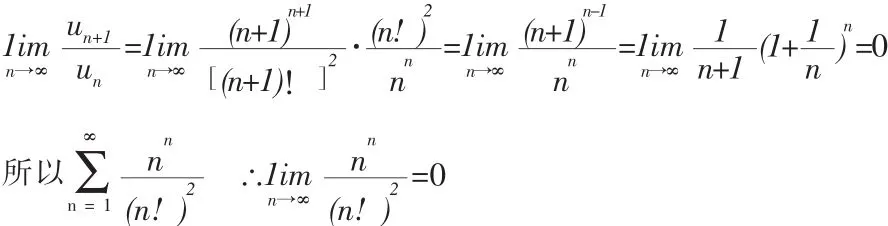
6.利用定積分求極限

利用定積分求極限，主要針對于求解項數無限增大的無窮小量之和的極限。求解步驟為：①將每一項都提出一個，提出后，剩下的式子表示為一個通項；②將問題轉化為通項公式所對應的函數在某一區間上的積分。

7.利用夾逼定理求極限

通常n個項按遞增或遞減排列時，用夾逼定理求解。

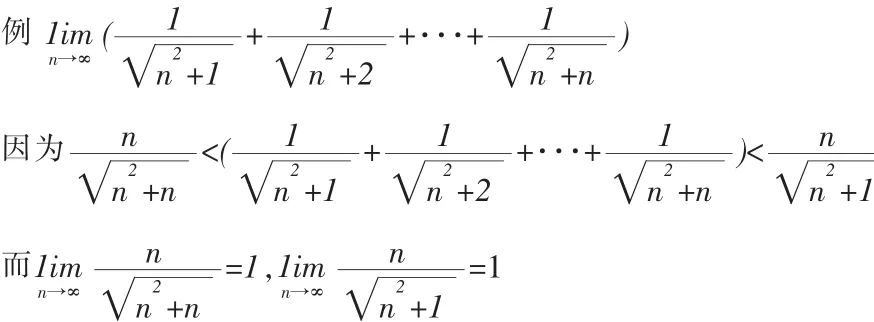
8.結語

上述歸納了針對高等數學中不同特點的數列極限一些常用求解方法。在做具體數列極限的求解時，應觀察數列的特點，選擇適當的方法靈活掌握。數列極限是高等數學中一個非常基礎的概念，對后續知識的學習起著至關重要的作用，對于數列極限的求解方法還有很多，將在今后的探索中進一步研究不斷完善。

［1］江濤.淺談數列極限的計算方法[J].科技信息.

［2］菲赫金哥爾茨.微積分教程.第一卷分冊[M].北京：人民教育出版社，1980.

［3］華東師范大學數學系.數學分析（上）[M].上海：高等教育出版社，2001.

［4］塔懷鎖.數列極限的幾種特殊求解方法[J].北京工業職業技術學院，2011，2.

As a very basic mathematical concept,Sequence Extremity is an important part in mathematics curriculum,and has vital application in higher mathematics.The calculation of Sequence and Extemity is a tough point to many students in learning calculus.This thesis will carry on a beneficial discussion by illustrating on a variety of ways which used to solve the Extremity.

Sequence Extremity；Solving method

張俊青（1982—），女，漢族，山西繁峙人，助教，畢業于鄭州大學，就職于山西職業技術學院，研究方向為信息與計算科學。

The discussion of Sequence Extremity proving in higher mathematics

O13

A

2095-7327（2016）-04-0150-02