向數學的縱深處邁進
——《面積的變化》教學

楊宏權 周正琴

【教學內容】

蘇教版六年級下冊第48～49頁。

【教學過程】

板塊一：從“一次爭論”說起……

出示：3cm的線段和比例尺 1∶1000。

讓學生敘述圖中信息，回憶什么是比例尺（板書：長度比），并讓學生算出圖上3厘米的實際距離。

出示：乒乓球活動室的平面圖。

引出“求球館的實際面積到底有多大？”健健和康康發生的爭論。

健健的想法：

2×3=6（平方厘米）

6×1000=6000（平方厘米）

6000平方厘米=0.6平方米

康康的想法：

2×3=6（平方厘米）

6×1000000=6000000（平方厘米）

6000000平方厘米=600平方米

引出猜想：面積比與長度比，會有什么樣的關系呢？通過“你打算采用什么樣的方法來研究這個問題”，激發學生思考，通過生生之間的交流，讓學生初步認識可以通過畫圖形、放大、算一算的方法進行判斷。

出示智慧心語：解決問題前，通常需要根據問題的特點設計解決問題的方案。

板塊二：由長度比到面積比。

1.舉例，初步感知。

以長方形為例，任意畫一個長方形。出示1cm×3cm的長方形，再把它放大并分別出示三個長方形：3cm×3cm、1cm×9cm、3cm×9cm。讓學生選一選，哪個是原長方形放大后的圖形？為什么？按什么比放大的？

接著讓學生算一算大長方形與小長方形的面積分別是多少？面積比呢？最后得出：大長方形與小長方形的面積比是9∶1。

2.提升，歸納規律。

通過上面的舉例，學生發現長度比是3∶1，而面積比卻是9∶1，得出“長度比并不等于面積比”，從而引發學生進一步思考：面積比可能與長度比存在怎樣的關系呢？再次引發學生猜想（面積比可能等于長度比的平方），并引導學生討論：根據一個例子我們能說面積比就一定等于長度比的平方嗎？（不能）從而得出：要想知道這一猜想是否具有普遍性，可以再舉些例子進行驗證。

出示：如果將小長方形按（ ）∶（ ）的比放大，放大后與放大前圖形的面積比是（ ）∶（ ）。

學生自由選擇，并獨立完成。然后選擇兩種用不同比放大的作業進行展示，觀察歸納。算出面積和面積比,指名講解。從而得出：把一個長方形按n∶1的比放大，放大后與放大前長方形的面積比是n2∶1。

這時教師再次激疑：通過舉例驗證，我們發現這樣的規律適合長方形，它是否也適用于其他平面圖形呢？從而將學生的探索思維向其他平面圖形延伸。

給出正方形、平行四邊形、三角形和圓等。讓學生選一種或幾種以前學過的平面圖形，再將它按一定的比放大，算一算、填一填，完成作業紙。反饋，指名上臺講解。逐個得出，這一規律同樣適用于正方形、平行四邊形、三角形和圓。總結得出規律：把一個平面圖形按n∶1的比放大，放大后與放大前圖形的面積比是n2∶1。

出示智慧心語：由特殊到一般，是驗證猜想的重要環節。

3.溯源，解釋規律。

教師引導：剛才我們得出的規律雖然已經通過實踐的檢驗，但是一個結論的得出還需通過科學的論證。以長方形為例，出示平面圖。

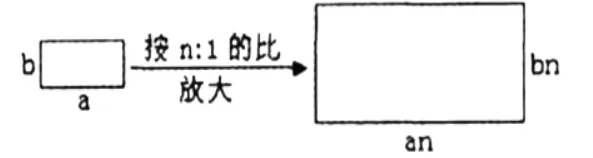
讓學生通過計算說明：

小長方形的面積：a×b=ab

大長方形的面積：（an）×(bn)=abn2

最后，引導學生發現，通過積的變化規律，揭示其中的奧秘。

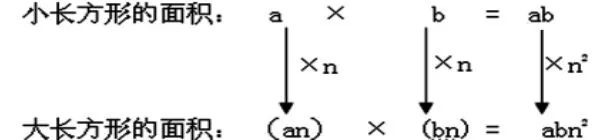
引導學生上下對比這兩道算式，并用以前所學的知識來解釋面積的變化規律。從而得出：一個因數擴大n倍，另一個因數也擴大n倍，積就擴大n2倍。

教師再次引導學生用積的變化規律來解釋其他的平面圖形長度比與面積比的關系。學生選擇其中一個平面圖形論證，先在作業紙上寫一寫，再說給同桌聽一聽。

出示智慧心語：追根溯源，就能找到規律的本質。

4.運用，豐富規律。

（1）解決乒乓球館問題。出示前面的例題，讓學生判斷一下，誰計算正確？健健錯在何處呢？再讓學生用新學的知識計算乒乓球活動館的實際面積。

2×3=6（平方厘米），6×10002=6000000（平方厘米），6000000平方厘米=600平方米。

（2）明明想給乒乓球活動館布置一張長9米、寬6米的乒乓球奧運冠軍的宣傳畫，如果按1∶30的比把宣傳畫縮小，縮小后這張宣傳畫的面積是多少?

9×6=54（平方米），54÷302=0.06（平方米）。

由此題引出：把一個平面圖形按1∶n的比縮小，縮小后與縮小前圖形的面積比是1∶n2。

5.回顧，積累經驗。

回顧我們探究與發現的過程。我們先通過長方形個例，有了猜想，再通過舉例子來檢驗，接著追根溯源論證了檢驗的結果，最終總結出了具有普遍性的結論。這樣一步一步地使得出的結論越來越縝密與完備。這也是我們解決問題的一般流程。（課件演示回顧過程）

板塊三：由 n2：1想到的……

牛頓有句名言：“沒有大膽的猜想,就沒有偉大的發明和發現。”教師再次激疑：根據長度比，如果給你大膽猜想的機會，你還會有哪些猜想呢？引導學生從面積，想到周長，再從平面圖形想到立體圖形。得出如下網絡。

學生有了猜想后，可試著讓學生驗證一下。全班匯報、交流。

出示智慧心語：大膽猜想，嚴密驗證，將會有更多的發現。

【課后思考】

思考1：整體性——從“一維教學”走向“三維思考”

教材中只介紹了從長度比向面積比的規律探索，其實細細思考，我們會發現，面積屬于二維空間，由長度和寬度兩個要素所組成的平面空間。而長度比則屬于一維空間的范疇，這時我們又在思考，那我們能不能從長度比再引導學生向三維空間（立體圖形）的體積比進行探索呢？教學實踐告訴我們完全可行。為此，課始我們通過比例尺的復習（一維空間），然后過渡到面積比的探索（二維空間），再到最后的知識總結與提升階段，激發學生對體積比產生新的猜想，這樣的設計，我們從整體出發，在知識三維過渡中培養學生整體的眼光、整體的思維，感悟智慧的生長。

思考2：抽象性——從“是什么”走向“為什么”

教學中，教師往往通過計算平面圖形的圖上面積和實際面積的比來找到變化的規律，對規律背后的本質問題，為什么會這么變化卻只字不提。這種研究僅僅局限在找現象規律，而數學是對現象的本質分析和探索，用數學方法研究這種現象正是我們要做的。面積屬于二維空間，它的大小決定于長度和寬度兩個變化量。這種變化與學生已學的積的變化規律是相通的。讓學生探究現象背后的實質不僅能提高學習效率，還能舉一反三，獲得更大的思維發展。

思考3：探索性——從“知識傳授”走向“素養形成”

通過“爭論”引發學生的思考沖突，并通過長方形放大前后的比較誘發學生直覺猜想，并通過計算比較，佐證猜想的正確。此時，又告訴學生一個特例的正確，還不能完全證明猜想的正確性。這時又引導學生用不同平面圖形的面積變化進行檢驗，從而進一步驗證猜想的合理性。然后又通過激發學生通過舊知，即積的變化規律進一步論證猜想的科學性，最后通過總結得出縝密的規律。這樣讓學生經歷“猜想——檢驗——論證——總結”的四個環節，循序漸進，步步深入，直覺思維與邏輯思維相互映照，這正是學生形成科學素養的過程。