淺談小學數學“空間與圖形”的教學策略
唐娟
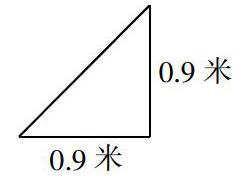
教師在教學中必須努力地搭建探究平臺,讓學生通過一系列的探究活動,從中進行觀察、操作、歸納、類比、猜測、變換和直觀思考,探究空間與圖形的特征及其內在聯系,逐步建立圖形的表象,才能真正發展學生的空間觀念. 如何通過搭建探究平臺來發展學生空間觀念呢?下面談談我的幾點看法.
一、選擇熟悉素材,提供感性支撐
學生的空間知識來自豐富的現實原型,與現實生活關系非常密切. 凡是學生熟悉的生活背景材料,都能激發學生對于空間與圖形的學習興趣,還能使學生深刻體驗內容豐富的圖形符號,發展空間觀念.
例如,在“位置與方向”的教學中,利用學生已有的上、下、前、后、左、右的方位知識和生活經驗,將學校周邊的景物拍成圖片,制作了學校及周邊街道、建筑物的方位示意圖,每小組分發一份,讓學生置身于實際的環境中理解方位之間的相互關系,動態地形成方位感;接著進行拼圖游戲:每小組分發一份中國地圖的拼圖卡片,讓學生進行拼圖,邊拼圖邊說明兩個省份的位置關系,如廣東在江西的南面,廣西在廣東的西面等. 學生在觀察、操作、描述、表達和交流等數學活動中,形成辨認東、西、南、北等方位的技能.
選擇學生熟悉的生活素材作為探究材料,能讓學生憑借已有的空間經驗,領悟空間知識,并形成把握空間知識的技能. 二、充實探究內容,誘發認知沖突
建構主義認為:學生的認知發展就是觀念的平衡狀態不斷遭到破壞,又不斷達到新平衡狀態的過程. 在空間與圖形的教學中,就是要通過充實探究的內容,破壞基于學生已有認知的平衡,繼而達到新的平衡狀態.
例如,有這樣一道題目:下圖是人民醫院包扎用的三角巾. 現在有一塊長18米,寬0.9米的白布,可以做多少塊三角巾?
學生解答這道題,有兩種方法,一是分別計算出長方形的面積和三角形的面積,用長方形的面積除以三角形的面積,求出三角巾的塊數;二是用長方形的長和寬分別除以三角形的兩條直角邊,再用求得的商相乘后所得的積乘2,求出結果. 為了讓學生能深入地探究三角巾與長方形布的關系,我把題目改為:—種等腰直角三角形的三角巾,直角邊長0.9米. 現在有一塊長18米,寬1米的長方形白布,可以做多少塊三角巾?雖然與原題相比只改動了一個數據,把長方形的寬“0.9米”改成了“l米”,但是為學生進行探究提供了可能. 改動后三角形的直角邊與長方形的寬不一樣長,如果再采用以上兩種方法來解決,顯然是行不通的. 學生必須采用畫一畫、剪一剪、拼一拼、分析數據特點等探究方法,才能正確利用長方形的長和寬與等腰直角三角形兩腰的關系來解決問題.
通過充實探究內容,學生對空間事物的形狀、大小、方位、變換關系和結構有了更深刻的理解,空間觀念得以形成和發展.
三、溝通知識聯系,積累空間表象
小學生對圖形的認識主要依賴于直覺觀察. 依照學生認識事物的這一規律,在空間與圖形的教學中,有必要引導學生聯系所學的知識,探究事物的特征,描述事物間的關系,積累空間與圖形的鮮明表象.
例如,“圖形的拼組”這一單元包含的知識點是長方形的對邊相等,正方形的四條邊相等,長方形與正方形邊的關系等. 教學時,我問學生:“同學們,你們見過風車嗎?知道風車怎樣做嗎?今天,我們就—起來做風車. ”接著讓學生參與到做風車的過程中,由對折長方形體驗長方形的對邊相等;沿對角線折正方形探究出正方形鄰邊相等,展開后又可以看出一個正方形是由四個三角形組成的;從長方形中剪出最大的正方形,體驗長方形與正方形的關系;最后折成了風車,又能讓學生體驗到平面圖形與立體圖形的關系,轉動風車同時還能看到運動的軌跡是個圓. 在這個探究過程中,學生既能體會到空間圖形內隱的知識,比如長方形、正方形的特征;又能感受到二維和三維空間之間的轉換,深刻領悟空間圖形的變換過程.
學生在探究活動中所形成的空間表象,是教師的語言表述或操作示范所代替不了的. 為此,教師在教學過程中應該重視溝通空間圖形之間的內在聯系,才能有利于學生更好地積累豐富的空間表象,有利于發展學生的空間觀念.
四、啟發猜測聯想,發展空間想象
愛因斯坦曾經說過:“想象比知識更重要,因為知識是有限的,而想象要概括世界的一切. ”想象是培養學生空間觀念的一個重要途徑. 在“空間與圖形”的教學中,誘發學生進行猜測和想象,不僅能滿足學生對未知事物的好奇心,而且可以發展其空間觀念,一舉兩得.
例如,在教學平面圖形的面積計算之后,設計了這樣一個探究活動,用—張紙擋住幾個不同的平面圖形的一部分,讓學生進行猜測:這張紙—個面是哪些已經學過的圖形?這些圖形的面積估計是多少?
學生獨立思考,然后小組交流,全班交流,得出:圖形①可能是直角三角形、正方形、長方形或直角梯形,圖形②可能是正方形、長方形或直角梯形,圖形③可能是平行四邊形或梯形,圖形④可能是三角形、平行四邊形或梯形. 接著猜測出這些圖形的面積,在此基礎上再進行驗證、計算. 這一探究活動設計具有挑戰性,能滿足學生的好奇心,激發學生去探究;同時又具有開放性,學生由已知圖形產生聯想,聯系學過的圖形特征,進行大膽地猜測,想象出白紙下面的圖形,及其與已知部分所組成的圖形,經歷了“猜測——假設——探究——驗證”的過程. 知道完整的圖形是什么并不重要,重要的是題目中潛藏的圖形觸發了學生的空間想象力. 在想象的過程中,學生對已學過的平面圖形的形狀、大小及其聯系有更進一步的理解和掌握.
在空間與圖形的教學中,教師應積極創設有利于學生猜測、想象的探究活動,使學生熟悉的幾何形體在他們的頭腦中重現、加工和改造,才能加深對這些幾何形體特征的認識.
總之,在空間與圖形的教學中,要把靜態的知識結論轉化為動態的探究對象,根據不同的教學內容,選擇有利于學生進行探究的方式、方法,搭建起探究的平臺,才能充分發展學生的空間觀念.

