美麗的陰影部分圖形

李漢平

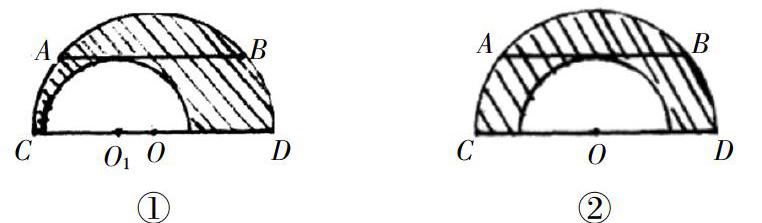
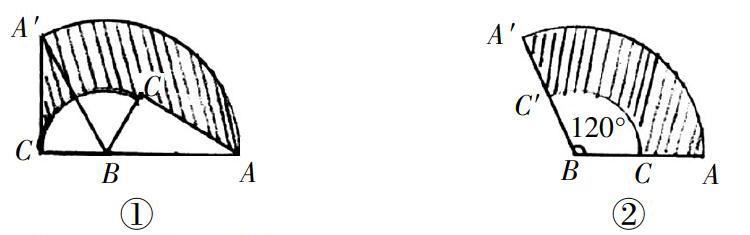
在初中數學《圓》這一章中，有很多求陰影部分面積的小題目，這是一類常見的基本題型. 有的題目，圖形直觀，能夠直接求出陰影部分的面積；但是，有的題目需要弄清圖形的構造特點，運用一定的技巧和方法才能求出陰影部分的面積. 求陰影部分面積常用的方法是將不規則的圖形面積轉化為規則圖形的面積后和與差. 下面介紹幾種常用的方法.

一、平移法

如圖①：兩個半圓中，長為24的弦AB與直徑CD平行且與小半圓相切，那么圖中陰影部分的面積為72 π.

分析 如圖①所示，將較小的半圓沿CD向右平移，使其圓心O1與較大的半圓的圓心O重合，變成圖②.這時，陰影部分就變成一個半圓環，由不規則圖形變成規則的圖形，進而求出陰影的面積為72 π.

二、旋轉法

如圖，在Rt△ABC中，∠BCA= 90°，∠BAC = 30°，AB = 8，把△ABC以點B為中心，逆時針旋轉，使點C旋轉到AB邊的延長線上點C′，則AC邊掃過的面積（圖中陰影部分）為16 π.

分析 由圖①結構可知：

S陰 = S扇形BAA′ + S△A′BC′ - S△ABC - S扇形BCC′ = S扇形BAA′ - S扇形BCC′

由已知條件可以算出這兩個扇形的圓心角都為120°，這樣陰影部分的面積實際上就是一個扇環的面積，（如圖②所示），從而很容易求出它的面積為16 π.

三、等積法

如圖①：AB為半圓O的直徑，C、D為半圓弧的三等分點，若AB = 12，則陰影部分的面積為6 π.

分析 連接CD，根據“同底等高，面積相等”的原理得到S△ACD = S△OCD，圖中的陰影部分的面積可轉化為圖②中扇形OCD的面積.

四、割補法

如圖，AB是☉O的直徑，C是半圓O上的一點，CD切☉O于點C，AD⊥CD，垂足為D，AD交☉O于E. 若E是的中點，☉O的半徑為1，則圖中陰影部分的面積為.

分析 由于E是的中點，所以弓形AE的面積等于弓形EC的面積，因此采用割補的方法，將圖①中的陰影部分轉化為圖②中的陰影部分. 在計算的過程中，要證明四邊形CDEF為矩形，運用勾股定理和垂經定理等，求出CD和DE的長.

五、重疊法

如圖，正方形的邊長為2，以各邊為直徑在正方形內畫半圓，則圖中陰影部分的面積為2π - 4.

分析 圖中的陰影部分是分別以正方形的四邊的中點為圓心，以各邊為直徑的半圓重疊而成的，每兩個半圓拼成一個圓，這樣陰影部分的面積就等于兩個圓的面積，減去正方形的面積.

在《圓》這一章中，求陰影部分面積的題目還有很多，求陰影部分面積的方法也很多，這里只列舉了幾種常用的方法，可供借鑒與參考. 每求出一個陰影部分的面積，就帶給我們美麗享受，技術的升華，大大打開解題的思路. 要達到爐火純青的地步，就需要在實際學習中廣泛做題，總結歸類，找出規律，以形成正確簡潔的方法.