基于MF—DFA的期指收益率標(biāo)度突變分析

常登輝

【摘 要】CSI300期指其收益率序列存在明顯的標(biāo)度突變點(diǎn)S*，該點(diǎn)將整個(gè)時(shí)間標(biāo)度一分為二，且每個(gè)標(biāo)度區(qū)間具有不同的多重分形特征及標(biāo)度指數(shù)。當(dāng)SS*時(shí)，收益序列其多重分形強(qiáng)度較弱，多重分形特征不明顯。

【關(guān)鍵詞】CSI300期指；標(biāo)度區(qū)間；多重分形特征

一、引言

作為現(xiàn)代金融分析體系的重要基礎(chǔ)，有效市場(chǎng)假說（Efficient Market Hypothesis，EMH）其實(shí)證結(jié)果并不理想[1-2]。與EMH不同，分形市場(chǎng)假說（Fractal Market Hypothesis，F(xiàn)MH）則認(rèn)為市場(chǎng)是一個(gè)非線性、開放、耗散的系統(tǒng)，投資者對(duì)市場(chǎng)信息的反應(yīng)是非線性的[3]。多重分形理論是這一領(lǐng)域應(yīng)用較廣泛的研究方法之一，被大量研究證明是刻畫金融市場(chǎng)復(fù)雜波動(dòng)特征的有力工具。

資本市場(chǎng)的多重分形特征表明金融時(shí)間序列并非在所有標(biāo)度區(qū)間上遵循相同的標(biāo)度規(guī)律。由于各交叉突變點(diǎn)的存在，標(biāo)度區(qū)間上的每個(gè)部分具有不同的多重分形特征及標(biāo)度指數(shù)，這就是標(biāo)度突變現(xiàn)象[4]。本文運(yùn)用多重分形理論，對(duì)2010年4月20日至2016年2月25日的CSI300期指（IF0001）日收益率的標(biāo)度突變現(xiàn)象進(jìn)行了實(shí)證分析。

二、MF-DFA分析法

多重分形消除趨勢(shì)波動(dòng)分析法（MultifractalDetrended Fluctuation Analysis，MF-DFA），可以有效驗(yàn)證一個(gè)非平穩(wěn)時(shí)間序列是否具有多重分形性[5]。

三、實(shí)證分析

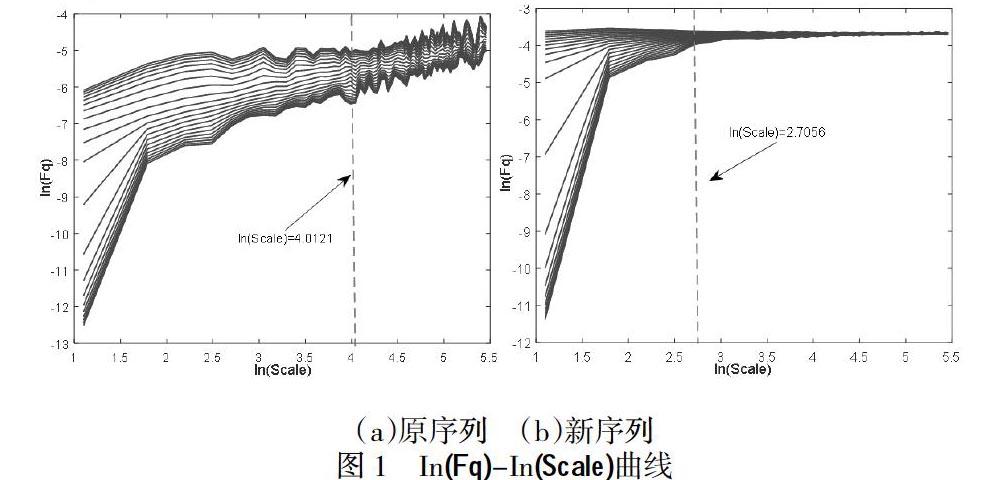
現(xiàn)在，運(yùn)用MF-DFA分析法來研究波動(dòng)函數(shù)Fq（s）隨Scale變化的關(guān)系，具體實(shí)證結(jié)果如圖1所示。圖中曲線從上至下其q=-10，-9，L，10。

觀察圖1（a）可以發(fā)現(xiàn)，F(xiàn)q（s）在In（S*）=4.0121，S*=55.2628，即S*≈55時(shí)，存在標(biāo)度突變，且突變點(diǎn)范圍不隨q的變化而變化。從圖1（b）可以看出，對(duì)于經(jīng)過打亂重排的序列（新序列），突變點(diǎn)的位置向左移動(dòng)，在，S*=14.9633，即S*≈55點(diǎn)處，且新序列在突變點(diǎn)處變化更大。

進(jìn)一步，在兩個(gè)不同標(biāo)度區(qū)間（即SS*）上運(yùn)用MF-DFA分析法對(duì)收益率序列進(jìn)行分析，其實(shí)證結(jié)果如圖2、圖3、圖4所示。

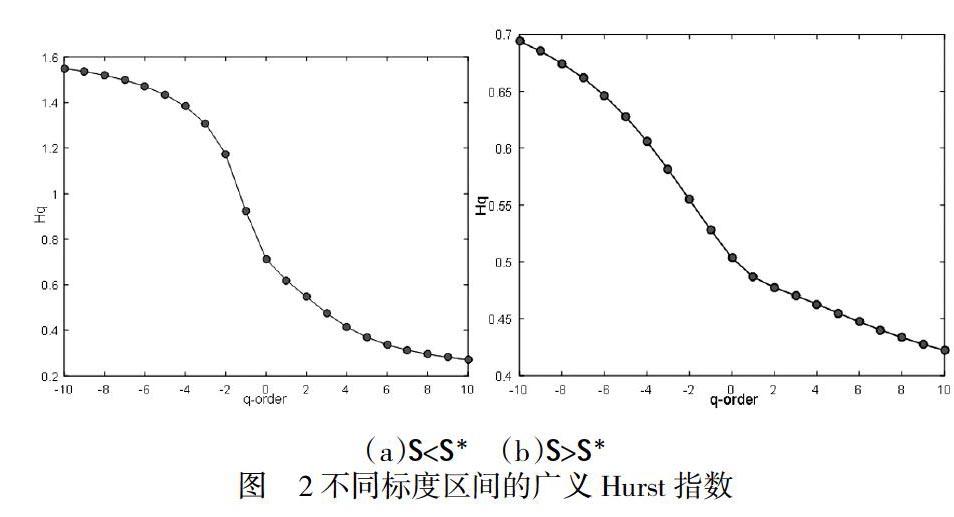
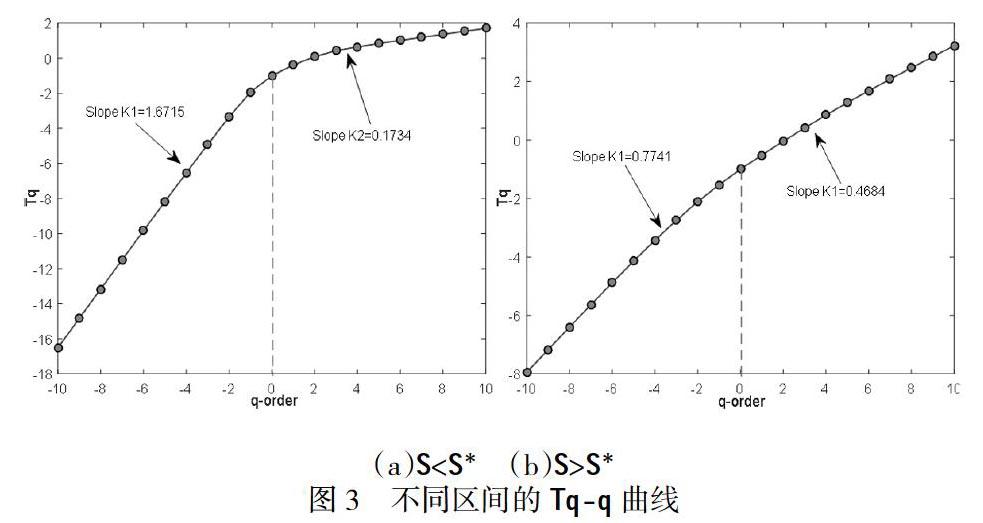
觀察實(shí)證結(jié)果可以發(fā)現(xiàn)，當(dāng)S

（1）如圖2（a）所示，當(dāng)q從-10變化到10時(shí)，收益率序列其廣義Hurst指數(shù)從1.5504遞減至0.2709，ΔH=1.2795且與q顯著相關(guān)，說明收益率存在明顯的多重分形特征；

（2）如圖3（a）所示，對(duì)于Tq，在q=0的兩側(cè)，其斜率不同。由于Tq其非線性越強(qiáng)，說明多重分形特征越顯著。因此在該標(biāo)度區(qū)間上存在顯著的多重分形特征；

（3）如圖4（a）所示，Δhg=0.3997<1.4982，再次說明收益序列在該標(biāo)度區(qū)間存在顯著的多重分形特征。由于H（2）=0.5473即為Hurst指數(shù)，因此當(dāng)S

（1）如圖2（b）所示，當(dāng)q從-10變化到10時(shí)，收益率序列的廣義Hurst指數(shù)從0.6941遞減至0.4222，但由于ΔH=0.2719<1.2795，說明收益率在該標(biāo)度區(qū)間存在較弱的多重分形特征；

（2）如圖3（b）所示，q=0兩側(cè)區(qū)間，Tq斜率分別為0.7741、0.4684，斜率的較小變化表明該標(biāo)度區(qū)間上的多重分形特征不顯著；

（3）如圖4（b）所示，Δhg=0.3997<1.4982，我們?cè)俅慰吹皆谠摌?biāo)度區(qū)間上收益率序列存在較弱的多重分形特征。此外，由H（2）=0.4776，說明此時(shí)收益序列表現(xiàn)為反持久性特征（即回歸均值的性質(zhì)）。

四、結(jié)語

CSI300期指在不同標(biāo)度區(qū)間遵循不同的標(biāo)度規(guī)律，這種標(biāo)度關(guān)系的不同說明了不同波動(dòng)程度的相關(guān)性不一樣，因此應(yīng)針對(duì)不同程度的風(fēng)險(xiǎn)采取不同的風(fēng)險(xiǎn)管理措施。一方面，相關(guān)投資者應(yīng)根據(jù)短線投資與長線投資的不同在實(shí)際操作中關(guān)注不同的影響股價(jià)的因素；另一方面相關(guān)監(jiān)管部門在政策法規(guī)的制定及執(zhí)行上要充分考慮到不同標(biāo)度區(qū)間的標(biāo)度特性，尤其是在進(jìn)行金融風(fēng)險(xiǎn)管理時(shí)要深刻理解資產(chǎn)收益率的分布及其波動(dòng)性特征。

【參考文獻(xiàn)】

[1]Zvi B， Robert CM. finance. Beijing： Publishing House of RenMin University of China， 199， 200-211.

[2]EF Fama. Efficient Capital Market： A review. Journal of Finance， 1970， 383：33-41.

[3]Peters E E. Chaos and order in the Capital Market [M]， New York： Wiley， 1991.

[4]Peters E E. Fractal market analysis [M]， New York： Wiley， 1994.

[5]何建敏，朱林，常松.中國股票價(jià)格波動(dòng)的尺度特性[J]，中國管理科學(xué)， 2003，10（3）： 1-5.