串列螺旋槳水動力性能的數值預報

王國亮，王　超，喬　岳，李　想（哈爾濱工程大學 船舶工程學院，黑龍江　哈爾濱 150001）

?

串列螺旋槳水動力性能的數值預報

王國亮，王超，喬岳，李想
（哈爾濱工程大學 船舶工程學院，黑龍江哈爾濱 150001）

摘要:為了分析串列螺旋槳的水動力性能，本文運用計算流體動力學理論，結合雷諾時均 RANS 方程和相對運動參考坐標系對其三維定常粘性流動進行數值模擬。應用 Fortran 語言編制程序計算螺旋槳的型值點，并采用三次樣條曲線擬合各點，建立串列槳三維模型。 以某一串列螺旋槳作為研究對象，得到螺旋槳的推力系數、轉矩系數以及流域內速度分布等水動力特性參數，并給出敞水性能曲線。計算結果與試驗數據吻合較好，驗證了數值方法的可行性和準確性。

關鍵詞：串列螺旋槳；水動力性能；CFD；粘性流場；數值模擬

0　引　言

串列螺旋槳是一種將2部普通螺旋槳裝于同一尾軸上的特種推進器。與普通螺旋槳相比，在總盤面比相同，負荷較重或直徑受限制時，串列螺旋槳的效率有著相當提高，并能改善船舶尾部的震動；與其他特種推進器相比，其構造簡單，易于制造加工和檢驗維修[1]。事實上，20世紀60年代以前相當長的一段時間內串列螺旋槳并沒有得到發展。之后，考慮到船舶振動和節能，國內外學者對串列螺旋槳產生新的興趣，相繼做了一些研究[2–3]，也取得一些進展。但總體來說，目前國內外關于串列螺旋槳的研究仍較少，只有少量模型系列試驗和設計圖譜，對其水動力性能進行數值模擬的研究更是少之又少。近年來，由于船舶主機功率的急速增大，推進器負載和燃料消耗不斷提高，空泡、振動、噪聲和節能問題更加突出，再加之普通螺旋槳的研究日趨成熟，串列螺旋槳以其突出優點可望得到發展。

近十幾年來，隨著計算機技術的推廣普及和計算方法的不斷增多，計算流體力學（CFD）技術取得了蓬勃發展，在工程領域已得到廣泛應用。同時，采用RANS 方程數值求解普通螺旋槳敞水性能的研究已開展起來[4–8]。文中利用在船舶系統水動力性能預報方面得到廣泛認可的 Fluent軟件對串列螺旋槳的水動力性能進行數值模擬，得出不同進速系數下槳葉的敞水性能曲線，并將計算結果與理論值進行對比分析。同時，數值模擬也顯示出了螺旋槳槳葉處及流場內的速度分布情況。

1　數學模型

1.1控制方程

通過對參考水域的旋轉處理以及給平均來流設以相對速度。可認為螺旋槳軸向和周向均相對靜止的處于定常不可壓流體中，則流場的連續方程和動量方程分別為：

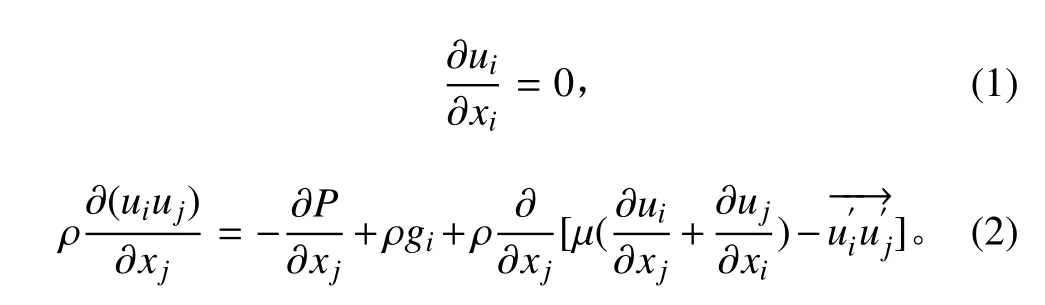
式中：ui和uj為速度分量時均值(i, j = 1, 2, 3)；P為壓力時均值；ρ為流體密度；μ為流體粘性系數；gi為重力加速度分量；為雷諾應力項。

方程中的雷諾應力項屬于新的未知量，因此要使方程封閉，必須對該應力項作某種假設，即建立應力的表達式（或引進新的湍流模型方程），通過表達式或湍流模型，把應力項中的脈動值與時均值聯系起來[9]。

1.2湍流模型的選取

雖然已有大量學者們對湍流問題開展研究，但由于湍流內在機理的復雜性，迄今尚未認定一種解決螺旋槳粘性繞流場數值計算中湍流問題的最佳方法。文中選取理論上發展較為完善，在工程上廣泛運用的 k-ε湍流模型的一種 RNG（renormalization group）k-ε來封閉 RANS 方程。與標準 k-ε 模型相比，RNG k-ε 模型通過修正湍動粘度，考慮了平均流動中的旋轉及旋流流動情況；其產生項不僅與流動情況有關，而且在同一問題中也是空間坐標的函數。所以 RNG k-ε 模型不但對充分發展的湍流依然有效，而且可以更好地處理高應變率及流線彎曲程度較大的流動。

RNG k-ε 模型是由 Yakhot 和 Orzag 把重整化群（RNG）方法引入到湍流研究中建立的一個新的湍流模型，其方程如下：

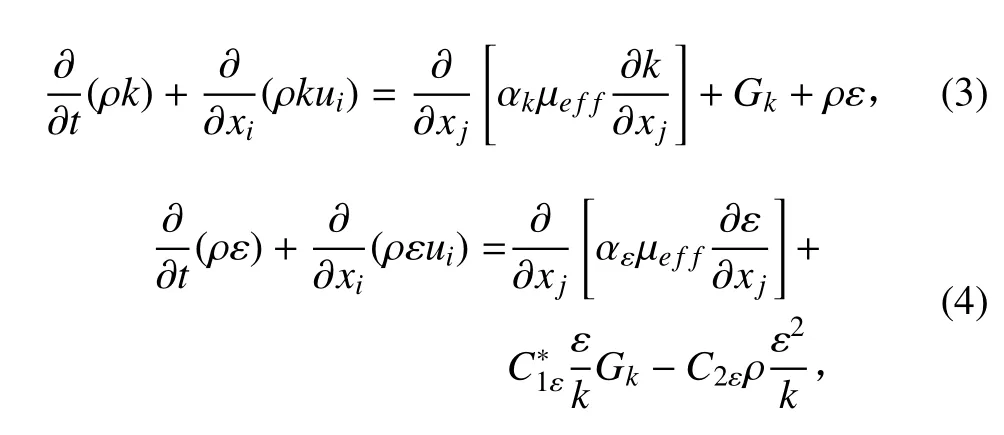
湍流粘性為：

2　數值計算過程

本文以標準 CLB4-55-1 串列螺旋槳[3]為例進行串列槳的水動力性能預報分析，其主要參數如表 1 所示。

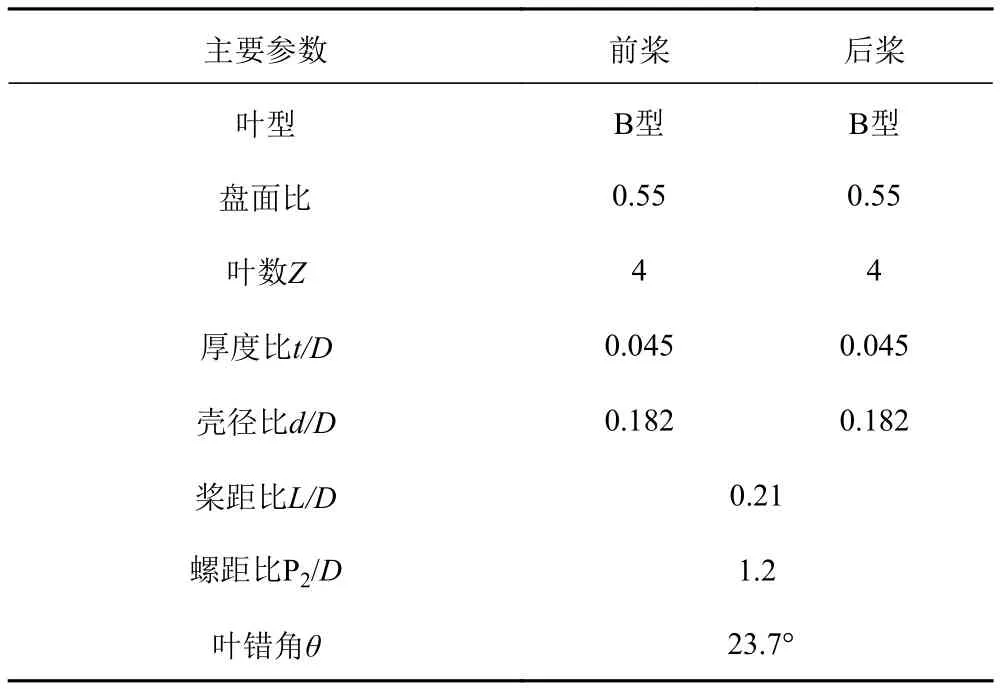
表1　CLB4-55-1 串列螺旋槳的幾何參數Tab. 1　Dimensions of CLB4-55-1 Tandem Propeller

與普通螺旋槳類似[9]，模型建立于直角坐標系。X軸定義為螺旋槳的旋轉軸，正方向指向下游與來流方向相同；Y 軸定義為螺旋槳槳葉的葉面參考線方向，由葉根指向葉稍；Z 軸滿足右手定則。螺旋槳葉面、葉背各個半徑處以及槳轂上的型值點由自編 Fortran 語言程序計算得到，對槳葉葉根及葉梢處型值點進行必要的插值修正和補充，以特定格式導入 ICEM 前處理軟件，并用 NURBS 樣條曲線去擬合處理型值點，由點到線，由線到面，由面到體，合成體前先保證了槳的封閉性，最終得到光順的三維串列螺旋槳模型，如圖1 所示。

網格劃分是直接影響模擬精度和效率的關鍵因素之一，高質量的網格是實現數值模擬成功的首要條件，過密或過疏的網格都應避免。過疏會導致數值解不精確，或使計算結果不收斂。而過密的網格則使得計算量大幅度增加，對計算機硬件要求提高，計算時間延長。鑒于非結構的舍去網格節點的結構性限制，節點和單元的任意分布；容易控制網格的大小和節點的密度；具有良好的貼體性及自適應性等特點。本文選用了非結構網格對螺旋槳和內域進行劃分以提高精度，如圖2 所示。

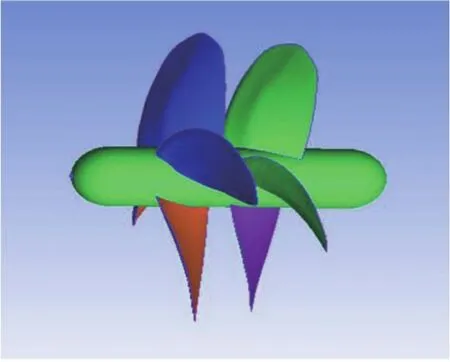
圖1　螺旋槳三維圖Fig. 1　The three dimension chart of the propeller

圖2　螺旋槳槳葉與槳轂網格劃分Fig. 2　Grid division of blade and hub

3　數值計算結果

3.1敞水性能曲線計算結果及與試驗的對比

進速系數J分別取為0.5，0.7，0.833，0.9，1.1，螺旋槳轉速為 n = 600 r/min，并以改變來流流速大小來實現進速系數的變化。計算得到的壓力通過槳葉表面的積分后得到不同進速系數下的螺旋槳槳葉的推力和扭矩值，換算得到推力系數 Kt和轉矩系數 Kq。并與試驗值進行比較。表 2 列出了在不同進速系數時的螺旋槳推力與扭矩。

從表 2 和圖3 可以看出不同進速系數下，串列螺旋槳的推力系數 Kt曲線和轉矩系數 Kq曲線的計算值和理論值有一致的變化趨勢、圖形基本吻合，在進速系數分別為：0.5，0.7，0.833，0.9，1.1 時，Kt、Kq的平均誤差分別為 4.24% 和 4.55%，在實際工程允許范圍內。尤其在螺旋槳負載較輕、進速系數大于 0.9時，曲線吻合程度更為理想。因而驗證了本文給出的串列螺旋槳水動力性能數值模擬方案的可行性和準確性。推力系數的計算結果和轉矩系數的計算結果總體偏小，可能由于文章所建立的模型與理論模型幾何形狀不完全相同，以及所用的離散格式和求解方法等因素對結果的影響共同造成的。總體而言，計算結果與理論值之間吻合很好，可以滿足工程需要。

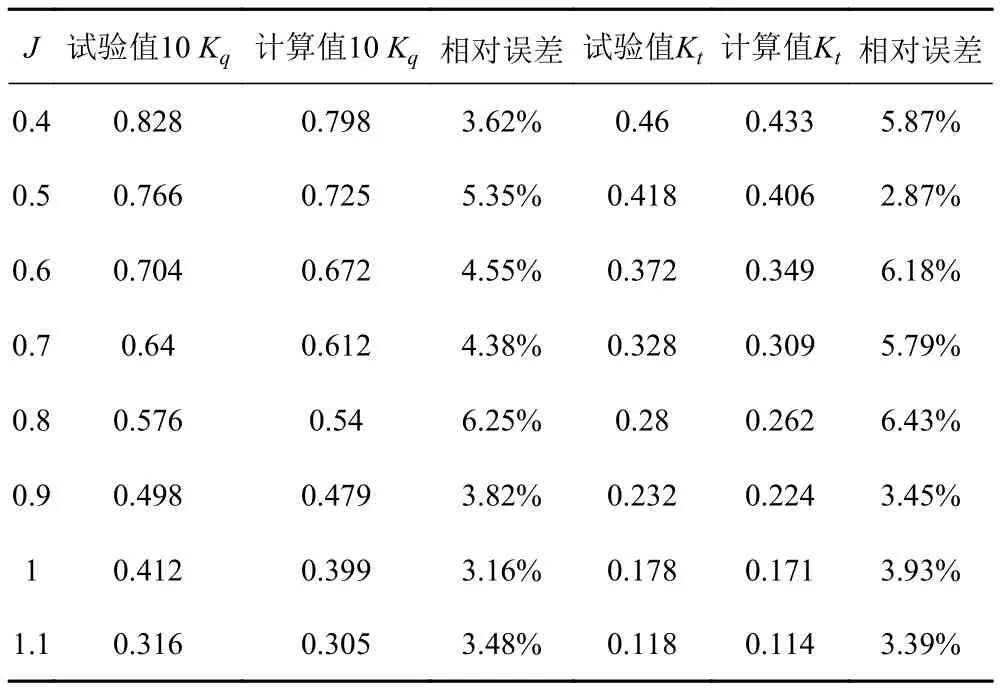
表2　計算值與試驗值對比Tab. 2　Comparison of the computed and experimental results

圖3　螺旋槳的敞水性能曲線Fig. 3　The curves of propeller’s open water performance

3.2旋轉域內各剖面處的速度分布

由于串列螺旋槳兩槳之間相互干擾作用，使周圍流場受到較大的影響。為更好地了解串列螺旋槳周圍流場的運動情況，本文給出相同來流速度下（V = 1 m/s）情況下，串列螺旋槳沿軸向的4個截面處的速度分布，包括前槳盤面（x = 0處）、兩槳之間（x = 0.1處）、后槳盤面（x = 0.2處）和尾流區（x = 0.32處）。

在圖4中，由于假定槳為靜止，故水流速度相對于槳為負值；切向速度在貼近槳葉區域從葉根到葉稍逐漸增大；對比 x = 0 和 x = 0.2 兩截面能發現，后槳盤面處的切向速度明顯小于前槳，這是由于考慮前槳周向干擾速度的影響，后槳的來流得到周向加速，相對于水流來說要比前槳轉的慢。

從圖5可以看出，軸向速度在各截面沿展向都呈現先增大再減小的趨勢。對比 x = 1 和 x = 0.32 兩截面處能發現尾流場處軸向速度略大于兩槳之間處；而對于前、后槳盤面處，軸向速度均受到來自對方和自己的軸向干擾速度影響故相差并不明顯。

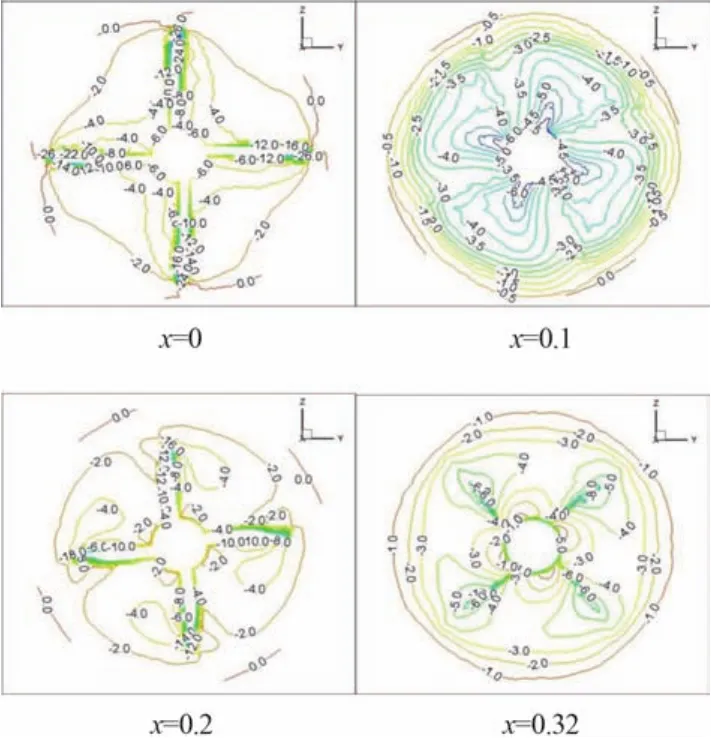
圖4　切向速度分布Fig. 4　Tangential velocity distribution

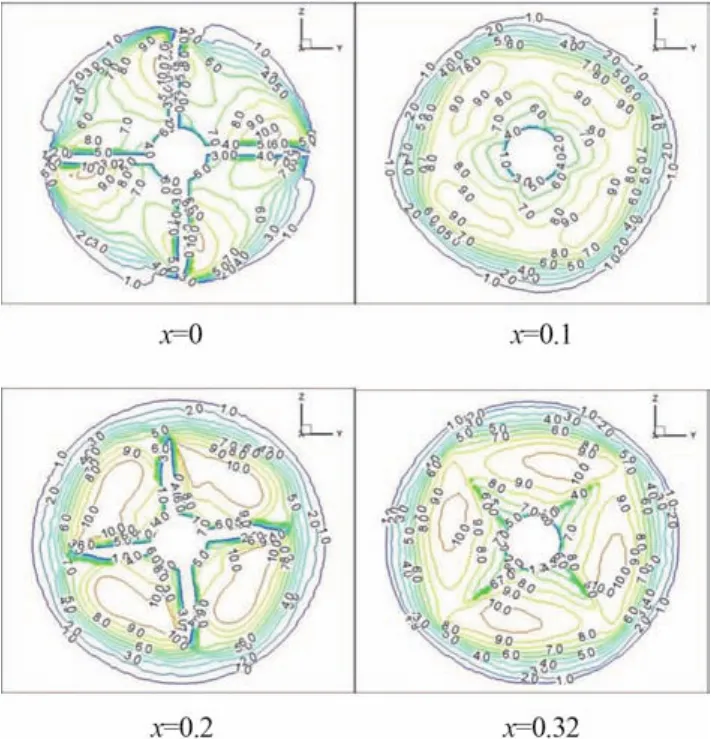
圖5　軸向速度分布Fig. 5　Axial velocity distribution

4　結　語

本文運用計算流體動力學理論，采用 RNG k–ε 湍流模型，結合 RANS 方程，對串列螺旋槳多個進速系數下的水動力性能進行數值模擬，由上述分析得到以下結論：

1）與實驗數據的比較可以發現，在螺旋槳的工作點附近，無論是推力系數還是扭矩系數，計算結果都和試驗數據吻合很好，表明 CFD 技術對串列螺旋槳敞水性能的計算有較高的預報精度，能較好地滿足工程需要。

2）對于進速系數大于 0.9 的情況下，螺旋槳負載較小，推力系數和轉矩系數的計算結果更接近于試驗值，具有更高的準確性。

3）串列螺旋槳前槳的旋轉使水流的運動狀態從直線流動變為邊流動邊旋轉，因而使后槳的來流得到周向加速，所以后槳相對于水流來說周向速度明顯小于前槳 ，即相對轉速低于前槳。

參考文獻：

[1]盛振邦, 劉應中. 船舶原理(下冊)[M]. 上海: 上海交通大學出版社, 2004.

[2]TITOFF I A, BISKOUP B A. Investigation into the possibilities of tandem propeller application with the aim of decreasing the variable hydrodynamic loads transmitted to a propeller shaft[C]//Proceedings of the 11th International Towing Tank Conference (ITTC). Tokyo, Japan: ITTC, 1966: 308–314.

[3]孫勤. 串列螺旋槳及其設計方法[M]. 北京: 人民交通出版社, 1983.

[4]錢錕, 陳慶任. 基于面元法和CFD的螺旋槳性能比較[J]. 艦船科學技術, 2011, 33(9): 36–39, 51. QIAN Kun, CHEN Qing-ren. Comparison between panel method and CFD for propeller performance analysis[J]. Ship Science and Technology, 2011, 33(9): 36–39, 51.

[5]劉應中, 張懷新, 李誼樂, 等. 21世紀的船舶性能計算和RANS方程[J]. 船舶力學, 2001, 5(5): 66–84. LIU Ying-zhong, ZHANG Huai-xin, LI Yi-le, et al. Calculations of the ship performances and solving of RANS equations in the 21st Century[J]. Journal of Ship Mechanics, 2001, 5(5): 66–84.

[6]FUNENO I. Analysis of steady viscous flow around a highly skewed propeller[J]. Kansai Society of Naval Architects, 1999, 231: 1–6.

[7]馮學梅, 陳鳳明. 使用Fluent軟件的螺旋槳敞水性能計算和考察[J]. 船舶, 2006(1): 14–19. FENG Xue-mei, CHEN Feng-ming. Calculation of propeller open water performance by CFD software Fluent[J]. Ship & Boat, 2006(1): 14–19.

[8]HUANG S, ZHU X Y, GUO C Y, et al. CFD simulation of propeller and rudder performance when using additional thrust fins[J]. Journal of Marine Science and Application, 2007, 6(4): 27–31.

[9]王超, 黃勝, 解學參. 基于CFD方法的螺旋槳水動力性能預報[J]. 海軍工程大學學報, 2008, 20(4): 107–112. WANG Chao, HUANG Sheng, XIE Xue-shen. Hydrodynamic performance prediction of some propeller based on CFD[J]. Journal of Naval University of Engineering, 2008, 20(4): 107 –112.

Numerical prediction of the propeller’s hydrodynamics performance

WANG Guo-liang, WANG Chao, QIAO Yue, LI Xiang
(Golloge of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China)

Abstract:In order to simulate numerically the tandem propeller hydrodynamics performance of steady viscous flow ,the computational fluid dynamics (CFD) method based to the Reynolds-averaged navier-stokes (RANS) equation and the moving reference frame technique is used in the paper. A 3D model of tandem propeller is built according to the points of propeller were calculated by Fortran program and optimized by the method of NURBS. such as thrust coefficients, torque coefficients and the velocity distribution. The computed results agree well with the experimental data such as thrust coefficients, torque coefficients and the velocity distribution. It shows that the numerical method has good accuracy in the prediction of tandem propeller open-water performance.

Key words:tandem propeller；hydrodynamic performance；CFD；viscous flow；numerical simulation

作者簡介：王國亮(1989–)，男，博士研究生，研究方向為船舶推進。

基金項目：國家自然科學基金資助項目(51309061); 中央高校基本科研業務費專項資金資助(HEUCFR1102)

收稿日期：2015–07–29； 修回日期：2015–09–06

文章編號：1672–7619(2016)3–0010–04

doi：10.3404/j.issn.1672–7619.2016.03.003

中圖分類號：U664.33

文獻標識碼：A