基于 CFD 預報雙槳式吊艙推進器水動力性能

祝志超，熊　鷹（海軍工程大學 艦船工程系，湖北　武漢 430033）

?

基于 CFD 預報雙槳式吊艙推進器水動力性能

祝志超，熊鷹
（海軍工程大學 艦船工程系，湖北武漢 430033）

摘要:基于粘性流體理論，采用CFD技術數值預報雙槳式吊艙推進器的敞水水動力性能。通過對某單槳吊艙推進器進行數值模擬，并與實驗值進行比較，驗證數值計算方法的準確性。最后數值計算了雙槳式吊艙推進器在不同偏轉角時的水動力性能，通過數值計算、結果比較和特性分析，計算結果呈現出一定的規律性，達到了給出雙槳式全回轉吊艙推進器數值預報的方法和一般性規律的目的，可以對此類推進器水動力性能的預報提供參考。

關鍵詞：雙槳式；吊艙推進器；CFD；水動力性能

0　引　言

隨著船舶對快速性的要求越來越高，如何尋找推進效率高的推進器一直是人們探究的重點。近年來，吊艙推進器集電機和螺旋槳于一體實現了模塊化設計，在船舶上的安裝布置也變得靈活，目前作為主推進器一般是吊掛在船尾下方。雙槳式吊艙推進器越來越受到人們的重視，隨之而來的，如何預報其水動力性能和操縱性能也成為了研究的重點之一。

雙槳式吊艙推進器的吊艙前后各裝有一個槳，所以在槳與槳、槳與吊艙以及裝在船后時與船之間的相互干擾，使得其水動力性能變得更為復雜。相比于傳統推式或拖式吊艙槳，雙槳式吊艙槳因后槳能吸收前槳尾流中的能量而能有效地利用更多的主機功率；相比于傳統軸傳動槳，前槳具有更均勻的進流比；吊艙通過支架懸掛在船體下面，體積小、重量輕、附加阻力小、效率高、空泡性能好[1–2]。

本文采用粘流 CFD 方法對雙槳式吊艙推進器敞水狀態下不同偏轉角時的水動力性能進行預報，希望得出預報此類吊艙推進器的一般特性。

1　CFD 原理

1.1控制方程

對于 N-S 方程的統計平均方法以及補充反映湍流特性的其他方程，如湍動能方程和湍流耗散率方程，是目前 CFD 的基本方法。

將湍流運動看作是時間平均和瞬時脈動的疊加，若不考慮瞬時脈動的影響，將 N-S 方程取時間平均，

即得到雷諾平均 N-S 方程，其方程為:

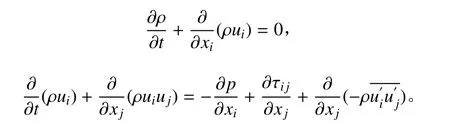
1.2湍流模型

由于湍流本身的復雜性，至今仍未找到一種解決湍流問題的最佳方法，而且目前關于吊艙推進器粘性流場數值計算方面的可供參考文獻較少，用來封閉RANS 方程的湍流模型中，理論上發展比較完善的有標準 k-ε 模型、RNG k-ε 模型及 SST k-ω 模型。

黃勝等[3]對湍流模型的選用做了相應研究，表明標準 k-ε 模型對螺旋槳水動力性能的數值預報存在明顯的缺陷；RNG k-ε 模型相對于標準 k-ε 模型有所改變，但這種改進仍然沒有拋棄基于渦粘性假設的基礎，因此其對預報精度的改進有限。

錢正芳等[4]做了不同湍流模型在吊艙推進器性能計算中的應用與比較方面的研究，通過3種湍流模型的計算結果與實驗數據的比較，分析在吊艙推進器數值模擬過程中湍流模型的適應性影響。結果表明，SST k-ω湍流模型綜合了 k-ω 湍流模型在近壁面計算的優點和k-ε 湍流模型在遠場計算的優點，同時增加了橫向耗散導數項，在湍流粘度定義中考慮了湍流剪切應力的輸運過程，其預報吊艙推進器敞水性能的精度較高。

SST k-ω 模型為了使標準 k-ω 模型在近壁面區有更好的精度和算法穩定性而發展起來，因此本文采用SST k-ω 模型。SST k-ω 兩方程湍流模型如下：

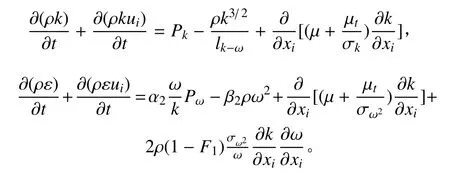
式中：PK和 Pω 為湍流生成項；F1為混合函數；S 為剪應力張量的常數項；σK，α2，β2，σω2均為經驗系數，σK= 2，α2= 0.44，β2= 0.082 8，σω2= 0.856；渦黏系數 μt由下式確定：

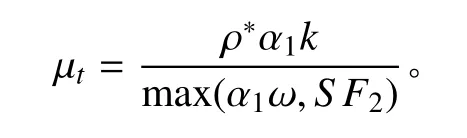
式中α1為待定常數。

1.3數值計算模型

多參考系模型（MRF）是將不同旋轉或移動速度的每個區域進行穩態近似，因此當邊界上流動區域幾乎均勻混合時，這種方法比較適宜，特別是在轉子和定子之間的交互作用相對較弱的時候。MRF 模型的整個計算域被分為多個小的子域，控制方程在每個子域內分別計算求解，在子域的交界面上則通過速度換算成絕對速度的形式進行各個子域流場信息的交換。但要精確模擬瞬態流場時，MRF 模型無能為力，可以求助于滑移網格。

2　計算模型

2.1螺旋槳模型

本文研究的是雙槳式吊艙推進器，其吊艙前后各裝有 1 部槳。采用 ICEM 建模的方法創建螺旋槳幾何模型，縮尺比為 1:10，螺旋槳模型的主要幾何參數如表 1，創建的三維模型如圖1 所示。

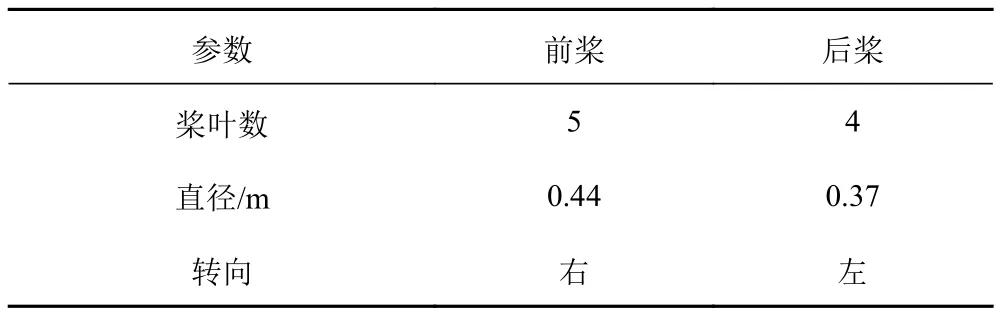
表1　螺旋槳主要幾何參數Tab. 1　The main geometric parameters of propeller

圖1　前后槳模型Fig. 1　Model of fore and aft propellers

2.2計算域及網格劃分

由于螺旋槳幾何外形的復雜性，建立單一計算域劃分結構或非結構網格都十分困難。本文采用結構-非結構混合網格進行離散，分塊建立計算域，在 ICEM上對吊艙單元進行網格劃分，對計算域劃分為3個區域：包含前槳葉的圓柱體旋轉域 1、包含后槳葉的圓柱體旋轉域 2 以及包含艙體和支柱的靜止域 3，見圖2。在2個旋轉域中對螺旋槳進行局部加密，提高計算結果的精確度；在域 3 上采用結構化網格，達到減少計算網格的目的。

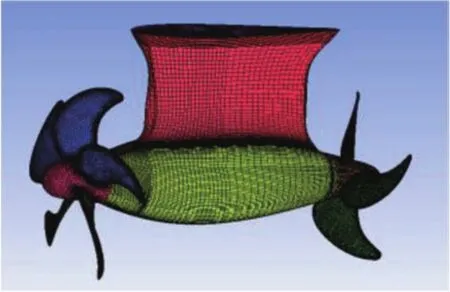
圖2　計算模型Fig. 2　Calculation model

2.3邊界條件設置及計算方法

對于此類雙槳式吊艙推進器，因為前槳、后槳及艙體支柱之間的相互干擾作用，后槳在前槳尾流中運動，并受到艙體和支柱的影響，其流動是非常復雜的，因此數值計算時參數的設定對計算精度的影響非常大。本文前后槳均采用多參考系模型，計算域如圖3 所示。入口邊界設置為速度入口，進速系數的變化通過改變來流速度實現，出口設置為壓力出口，物面設置為無滑移表面，基于壓力變量的 SIMPLE 耦合求解器，對流項和擴散項采用二階迎風差分格式進行離散，并用發展比較完善的 SST k-ω 湍流模型進行數值模擬，由于前后槳直徑不同，以前槳為基準取進速系數，前后槳槳模轉速均為 n = 1 500 r/min。通過偏轉全回轉推進器模型來實現偏轉工況的計算。

圖3　計算域網格劃分Fig. 3　The computational domain mesh

3　計算結果與分析

3.1計算方法驗證

由于資料有限，未能找到類似類型的雙槳式吊艙槳的試驗資料，為驗證計算方法的精度和可行性，對某船[5]的 VP 1458/VP 1459 單槳吊艙進行數值預報，將計算值與實驗值相比較，如表 2 所示。

從計算結果來看，無論是推力系數 KT，還是轉矩系數 10 Kq，其預報都較為準確。推力系數的誤差不大于 4.3%，轉矩系數的誤差不大于 3.95%，從而驗證了計算方法的精度和可行性，可以用來預報雙槳式吊艙推進器的水動力性能。

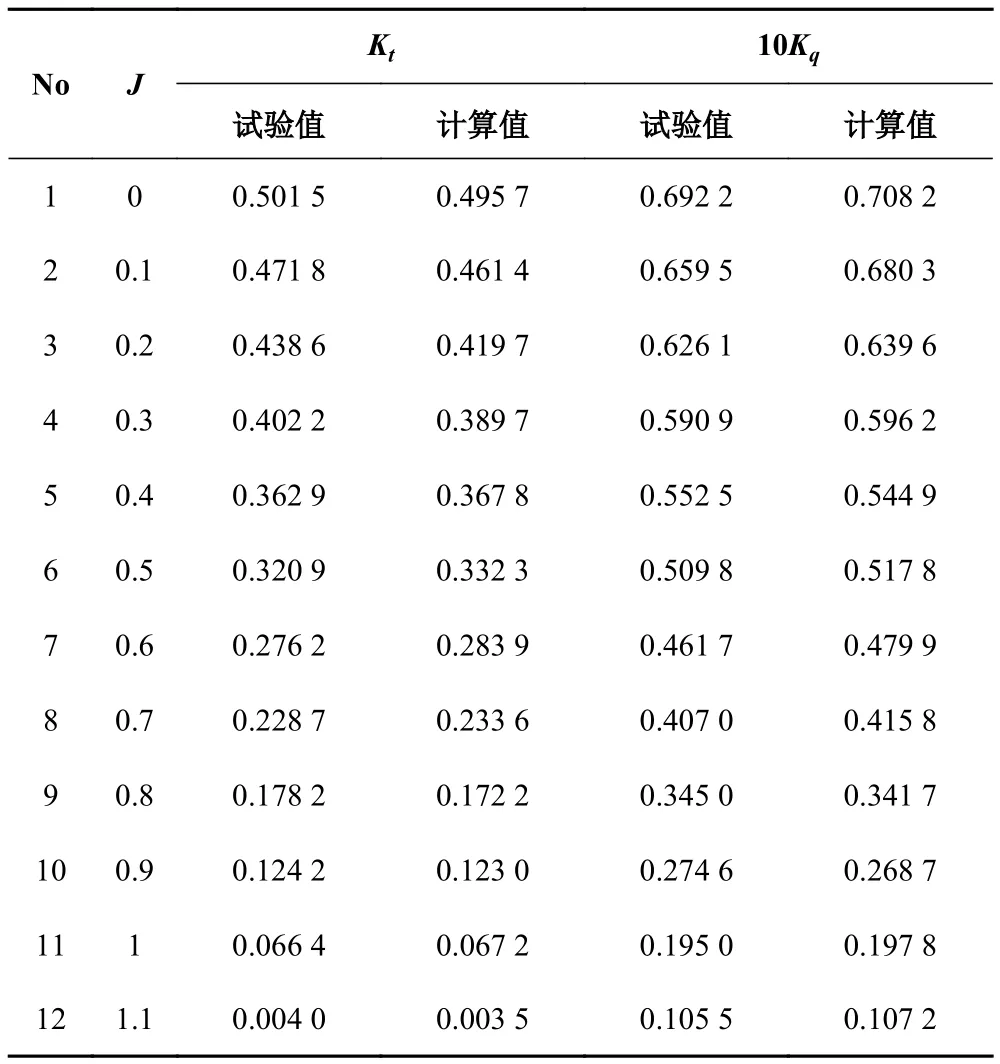
表2　計算值與試驗值比較Tab. 2　Comparison between the calculated results and test results

3.2給定工況及參數定義

在敞水下選取不同的偏轉攻角，分別為 0°，± 15°，± 30°，取不同的進速系數，得出不同攻角、不同進速系數 J 下前后槳的推力系數、扭矩系數以及吊艙單元的推力系數、轉矩系數和橫向力系數等。其中

式中：Vm為來流速度，ρ 為流體密度，下標 FP 為前槳，下標 AP 為后槳。其中，各個力與力矩的定義分在2個坐標系上，一個是固定在吊艙推進器上的移動坐標系 o-xyz，x 軸定義為從后槳向前槳為正，y 軸定義為從后槳向前槳看時指向左側為正，z 軸滿足右手定則；另一個坐標系 O-XYZ 為固定坐標系，不隨吊艙的偏轉而偏轉，它在 0°偏轉角時，與 o-xyz 重合，兩坐標系之間的關系如圖4 所示，偏轉角如圖所示時為正[6]。

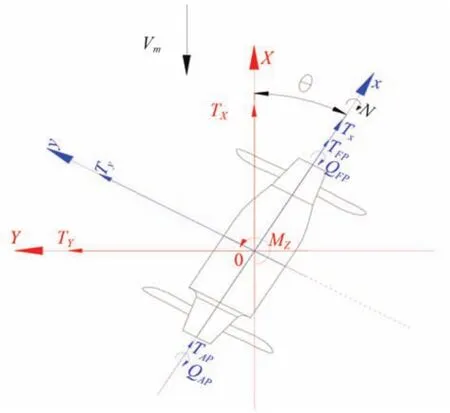
圖4　兩個坐標系Fig. 4　Two coordinate systems

3.3前后螺旋槳水動力性能

圖5～圖8 給出不同偏轉角下，前后螺旋槳的推力系數與扭矩系數隨進速系數的變化曲線圖。

圖5 與圖7 分別給出不同偏轉角時前槳的推力系數與扭矩系數隨進速系數的變化曲線，可以看出前槳推力系數與扭矩系數隨偏轉角的增大而增大，在低進速時變化不明顯，在高進速時差距增大。隨著偏轉角的增大，推力系數與扭矩系數增大，但左右偏轉角時的推力基本相同。其變化趨勢與常規同等螺距螺旋槳敞水特性比較相符，表明艙體與后槳對前槳的影響相對較小。圖6 與圖8 給出的是不同偏轉角時后槳的推力系數與扭矩系數隨進速系數的變化曲線，可以看出后槳推力系數隨著偏轉角從負變正而逐漸減小。其變化趨勢相對前槳較為平緩，其負荷幾乎只為前槳的一半，說明后槳受前槳和艙體的影響較大。

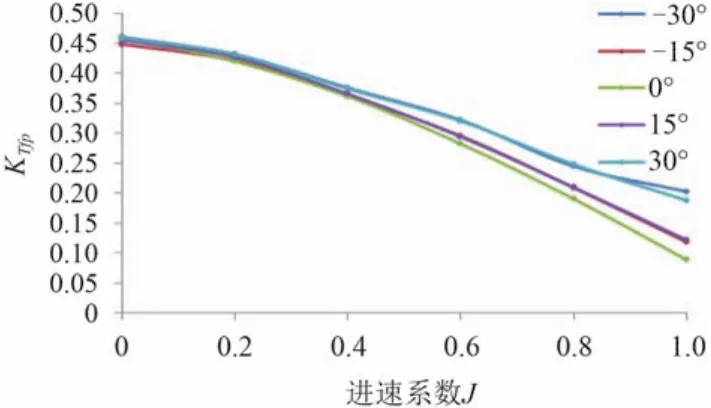
圖5　不同偏轉角時前槳推力系數曲線Fig. 5　The thrust coefficient curves of fore propellers at different deflection angles

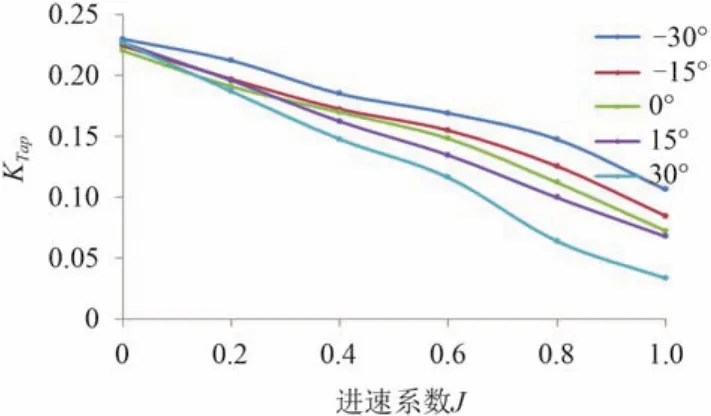
圖6　不同偏轉角時后槳推力系數曲線Fig. 6　The thrust coefficient curves of aft propellers at different deflection angles

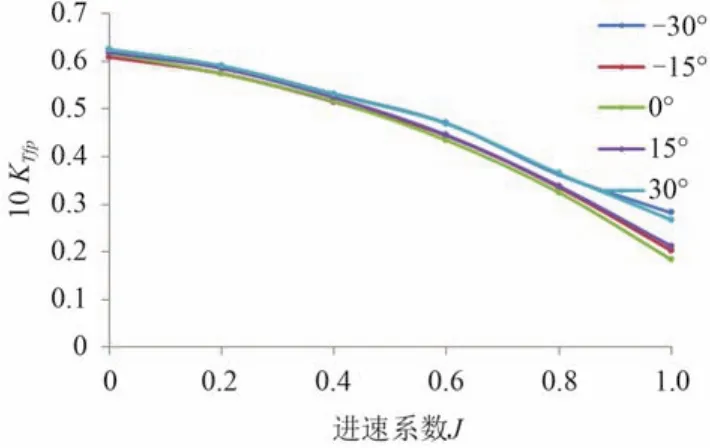
圖7　不同偏轉角時前槳扭矩系數曲線Fig. 7　The torque coefficient curves of fore propellers at different deflection angles

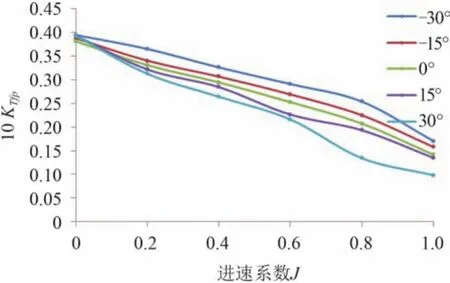
圖8　不同偏轉角時后槳扭矩系數曲線Fig. 8　The torque coefficient curves of aft propellers at different deflection angles

圖9 ～圖14 給出不同進速系數下，前后螺旋槳的推力系數與扭矩系數隨偏轉角變化的曲線圖。

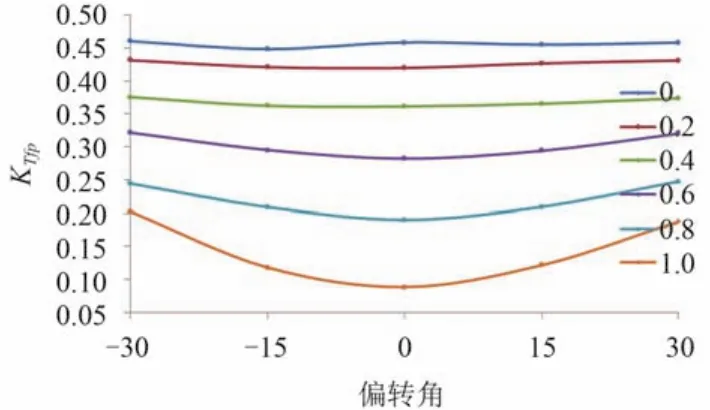
圖9　不同進速系數時的前槳推力系數Fig. 9　The thrust coefficient curves of fore propellers at different advance coefficients

圖9 與圖10 分別給出不同進速系數時前槳推力系數與扭矩系數隨偏轉角變化的曲線圖，可以看出在同一偏轉角下前槳推力扭矩系數都隨著進速系數的增大而減小；在同一進速系數下前槳推力扭矩系數都隨著左右偏轉角的增大而增大，是因為隨著螺旋槳的偏轉，有效進速系數逐漸減小。

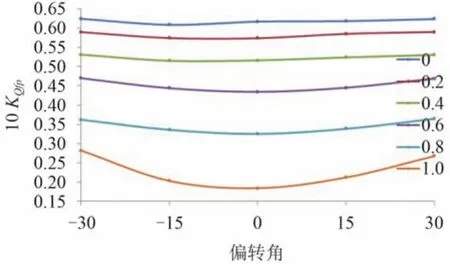
圖10　不同進速系數時的前槳扭矩系數Fig. 10　The torque coefficient curves of fore propellers at different advance coefficients

圖11 與圖12 分別給出不同進速系數時后槳推力系數與扭矩系數隨偏轉角變化的曲線圖。與前槳的變化規律不同，后槳的推力扭矩系數隨偏轉角從負到正而減小，進速系數越大，減小的趨勢月明顯。原因是后槳處于前槳和吊艙后，前槳的偏轉、尾流的加速、旋轉和壓力分布的變化以及艙體的阻塞對后槳水動力性能產生的影響。

前槳推力、扭矩系數在左右偏轉角相同時幾乎相等，即左右偏轉時對前槳的影響對稱，表明前槳的來流均勻，受后槳及吊艙體的影響很小；后槳推力、扭矩系數在左偏轉時比右偏轉時大，即左右偏轉時對后槳的影響非對稱，表明前槳的偏轉、尾流的加速、旋轉以及艙體的阻塞在左右偏轉時對后槳的影響也非對稱。

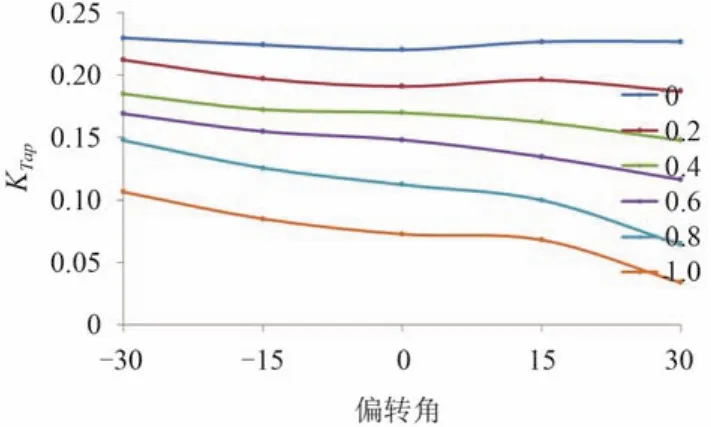
圖11　不同進速系數時的后槳推力系數Fig. 11　The thrust coefficient curves of aft propellers at different advance coefficients

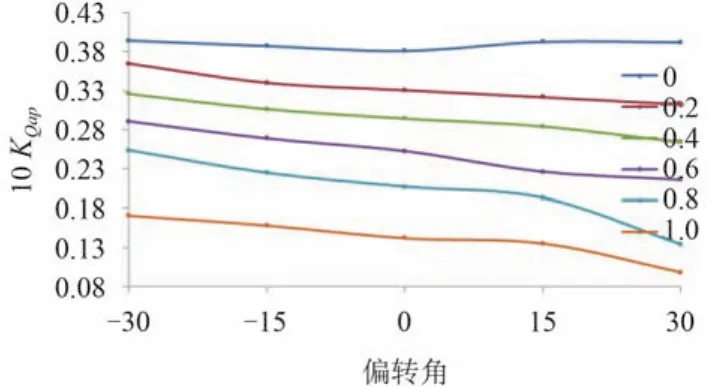
圖12　不同進速系數時的后槳扭矩系數Fig. 12　The torque coefficient curves of aft propellers at different advance coefficients

3.4吊艙單元水動力特性

圖13 ～圖16 依次給出吊艙單元推力系數、橫向力系數以及轉矩系數隨舵角和進速系數的變化。

在每個工況下，隨著進速系數的變化，吊艙推進器推力系數都幾乎成線性下降；推力系數隨偏轉角的增大而減小。

由于螺旋槳的旋轉，使得吊艙推進器受到橫向力，但由于前后螺旋槳旋向不同，橫向力相互抵消了一部分，所以在直流工況下，吊艙推進器橫向力系數很小；隨著偏轉角的增大，橫向力增大，且橫向力方向與偏轉角方向相同。

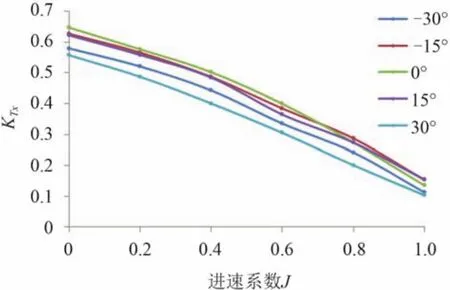
圖13　吊艙推進器推力系數Fig. 13　The thrust coefficient of pod propulsion

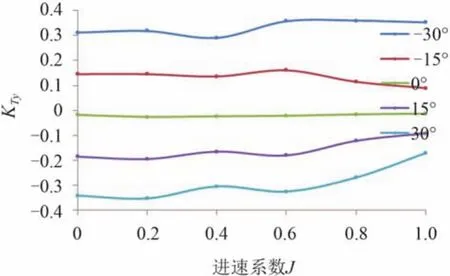
圖14　吊艙單元橫向力系數Fig. 14　The lateral force coefficient of pod propulsion

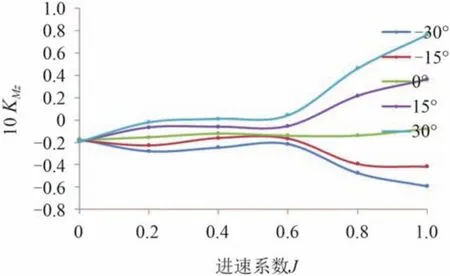
圖15　吊艙單元轉矩系數Fig. 15　The torque coefficient of pod propulsion

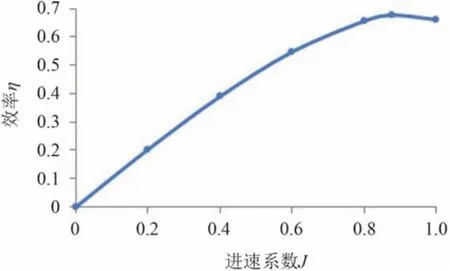
圖16　0° 偏轉角時吊艙推進器的敞水效率Fig. 16　Pod thrusters open water efficiency at deflection of 0°

在 0° 偏轉角時，吊艙推進器扭矩系數很小，幾乎為0。在低進速系數時，吊艙推進器扭矩系數都為負。隨著偏轉角的增大，吊艙推進器扭矩系數增大，扭矩的方向與偏轉角的方向一致。

圖16 給出吊艙推進器在直流工況下的敞水效率曲線，在 J = 0.877 8 時，效率最大，達到 0.677。

4　結　語

本文以雙槳式全回轉吊艙推進器為對象，采用RANS方法預報全回轉吊艙推進器在不同偏轉角度下的水動力性能，得出其推力系數、轉矩系數、及橫向力系數，研究結論主要有以下幾點：

1）吊艙艙體對前槳與后槳都有一定的影響，但對后槳的影響比較大，原因是后槳處于前槳和吊艙后，前槳尾流的加速、旋轉和壓力分布的變化以及艙體的阻塞對后槳水動力性能產生的重要的影響。

2）吊艙推進器的橫向力與扭矩均隨著偏轉角的增大而增大，推力則隨偏轉角的增大而減小。

3）與傳統槳舵推進系統相比，全回轉吊艙推進器有著更好的操舵效果，使艦船有著更好的機動性、操縱性，能實現原地回轉甚至倒車。

在所進行的工況下，吊艙推進器水動力性能隨偏轉角和進速系數的變化規律清晰，可為全回轉吊艙推進器的設計以及實船應用提供一定的參考。

參考文獻：

[1]熊鷹, 盛立, 楊勇. 吊艙式推進器偏轉工況下水動力性能[J].上海交通大學學報, 2013, 47(6): 956–961. XIONG Ying, SHENG Li, YANG Yong. Hydrodynamics performance of podded propulsion at declination angles[J]. Journal of Shanghai Jiaotong University, 2013, 47(6): 956–961.

[2]REICHEL M. Manoeuvring forces on azimuthing podded propulsor model[J]. Polish Maritime Research, 2007, 14(2): 3–8.

[3]黃勝, 王超, 王詩洋. 不同湍流模型在螺旋槳水動力性能計算中的應用與比較[J]. 哈爾濱工程大學學報, 2009, 30(5): 481 –485. HUANG Sheng, WANG Chao, WANG Shi-yang. Application and comparison of different turbulence models in the computation of a propeller's hydrodynamic performance[J]. Journal of Harbin Engineering University, 2009, 30(5): 481–485.

[4]馬騁, 張旭, 錢正芳, 等. POD推進器技術發展及其應用前景[J]. 船舶工程, 2007, 29(6): 25–29. MA Cheng, ZHANG Xu, QIAN Zheng-fang, et al. Technology development and its application prospect of POD thrusters[J]. Ship Engineering, 2007, 29(6): 25–29.

[5]GüNTHER B. Resistance test, propulsion test and wake measurement[R]. Potsdam: SVAtech GmbH, 2006: 13.

[6]賀偉, 陳克強, 李子如. 串列式吊艙推進器操舵工況水動力試驗研究[J]. 華中科技大學學報(自然科學版), 2015, 43(1): 107–111. HE Wei, CHEN Ke-qiang, LI Zi-ru. Experimental research on hydrodynamics of tandem podded propulsor in azimuthing conditions[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition), 2015, 43(1): 107–111.

Research on the CFD prediction method of hydrodynamic performance of tandem type podded propulsor

ZHU Zhi-chao, XIONG Ying
(Naval Engineering Department, Naval University of Engineering, Wuhan 430033, China)

Abstract:Based on viscous fluid theory, the hydrodynamics performance of tandem type pod propeller was discussed by using CFD technology. Then by numerical simulation of a single screw podded propulsor, and compared with the experimental results to verify the accuracy of numerical calculation method. The hydrodynamic performance of tandem type podded propulsor with different deflection angles is calculated by using the suitable numerical model and method. The results show an agreeable regularitywill provide reference for the prediction of hydrodynamic performance of tandem type podded propulsor.

Key words:tandem type；podded propulsor；CFD；hydronamic performance

作者簡介：祝志超 (1991–)，男，碩士研究生，研究方向為艦船流體動力性能。

收稿日期：2015–09–09

文章編號：1672–7619(2016)03–0014–06

doi：10.3404/j.issn.1672–7619.2016.03.004

中圖分類號：U664.3

文獻標識碼：A