基于領導跟隨的船舶航跡控制

齊小偉 任 光（大連海事大學 輪機工程學院 大連116026）

?

基于領導跟隨的船舶航跡控制

齊小偉 任 光
（大連海事大學 輪機工程學院 大連116026）

［摘 要］無人艇協同編隊控制具有重要的軍事和商船應用前景。利用多智能體聚集模型，基于leader-follower的目標跟蹤，實現了含有模型不確定性與未知海浪流干擾項的多無人艇協同編隊控制。采用單隱層神經網絡逼近船舶整體未知項和環境干擾，引入一階濾波器代替反步計算中的微分項,顯著減少了計算量。利用時-空解耦方法，各船舶通過交互航跡參數信息，間接實現分散協同編隊控制。利用Lyapunov穩定性分析方法，證明閉環系統所有狀態和信號收斂于一有界集。通過選擇合適參數，可使控制精度誤差范圍為任意小，仿真結果驗證了控制算法的有效性。

［關鍵詞］無人艇；神經網絡；不確定性；多智能體；一階濾波器；編隊控制

任 光（1952-），男，博士，教授，博士生導師，研究方向：輪機自動化與控制，復雜系統建模。

引 言

近幾十年來，隨著海洋的快速開發，各國在海洋經濟和軍事活動日益頻繁，使船舶編隊控制成為船舶運動研究中的熱點問題。多船編隊相對于單船具有容錯性和適應性等優點，在艦隊協同作戰、大洋航行補給、石油天然氣探測、環境監測、自動牽引作業中得到廣泛應用。無人水面艇（Unmanned surface vessel）是一種新型智能水面機器人，具有偵察、探測、掃雷、情報收集、反潛等功能，近年在民用和軍事領域得到廣泛應用。目前，典型代表有英國“Springer”號雙體USV、美國的“SpartanScout”、以色列的“Protector”等。

船舶編隊控制方法可分為行為控制法［1-2］、虛擬結構法［3］、勢函數法［4］、領導跟隨法［5］等。行為控制法給編隊中逐一指定一些包括隊形保持、障礙物避讓、目標搜索等預期行為。通過各行為的加權形成整個編隊的期望行為，不基于個體準確模型。領導跟隨法是基于多智能體群集運動控制的概念［6］，在由領航者和跟隨者兩種個體組成的群體模型中，跟隨者通過相互間的局部感知和相互協同作用，與領導者保持狀態相似，使船隊整體最終呈現一致行為。在船舶編隊領域，領導跟隨法屬于協同目標跟蹤。具體方法是指定一艘船為引導者，引導者跟蹤事先定義好的路徑軌線，其他船舶只需跟隨引導船的特定參考位置，可以是船舶中心，也可是船外某一虛擬位置，靈活多變、簡單易行，參看圖1。虛擬結構法中，將整個編隊作為一個剛體結構，編隊成員跟蹤其在剛體上對應的固定點，并使用隊形反饋防止單艘船掉隊，在一定程度上可看作領導跟隨法的一個變體。編隊控制中大多采用此兩種方法相互結合，發揮彼此優點。

圖1　領航船舶和跟蹤船舶隊形結構

船舶編隊協同控制，可利用協同路徑跟蹤和目標跟蹤來實現。協同路徑跟蹤［7］，提前設定好每艘船的期望路徑，利用通信網絡，實時交互各艘船行駛速度及路徑參數，直接在模型控制中加入隊形協調反饋，使這些參數達到一致。但是需引入輔助狀態變量，并且每艘船的路徑需要提前設定好，實現較為繁瑣。采用目標跟蹤［8］，可通過時空解耦思想使控制簡單化。首先實現空間上單艘船的路徑跟蹤控制，采用基于引導跟隨法追蹤劃定路徑上的虛擬船舶，使之能夠按指定路徑航行，參看圖1。隊形控制，即船舶在跟蹤路徑同時使速度趨于一致，屬時間域協同。通過時間域內的速度協同與空間域上的路徑跟蹤實現隊形控制，但兩者無優先順序。例如，如果隊形中引導船速度過快，跟隨船位置偏差過大，那么降低引導船速度，控制器會使跟隨船加速跟上引導船，縮小位置差距，保持既定隊形。當偏差距離縮小后，可以增大引導船速度，跟隨船在控制器作用下相應提高速度跟隨虛擬參考點，保持船舶隊形。

編隊首先需要解決單艘船舶的路徑跟蹤問題。國內外的許多學者對此作了大量的研究，取得了豐碩的成果，參見綜述［9］。大部分船舶在橫向沒有配備驅動裝置（例如側推裝置），船舶只能通過縱向主機推力和舵機控制前進速度和方向，不能直接控制橫向運動，都屬于欠驅動［10］。實際船舶由于其復雜性、水動力阻尼、未建模動態、環境干擾等，難以量化精確，得不到精確的模型。文獻［11］取消了船舶附加質量，阻尼矩陣為對稱陣假設，加入非線性阻尼和風浪干擾，設計了全局魯棒控制器。由于采用 Lipschitz映射算法自適應估計非線性項，使控制器比較復雜，其仍然是基于模型的控制［12］。該文獻也研究單個水下航行器的目標跟蹤問題，基于反步法和領導跟隨策略設計了自適應位置跟蹤控制器。文獻［13］利用模糊控制器，研究具有魯棒效應的自適應船舶控制器來跟蹤直線航跡。文獻［14］利用單神經網絡對模型未知不確定項進行估計（未考慮時變干擾項），基于協同路徑跟蹤，實現了編隊的自適應魯棒控制。文獻［15］利用RBF神經網絡作為前饋補償，設計了全局穩定自適應的魯棒路徑跟蹤控制器（屬于單艘船舶路徑跟蹤），但是高斯函數中心點及帶寬的選擇在實際應用中需試湊。文獻［16］在周期時延通信拓撲條件下，首先利用控制器控制單船跟蹤期望路徑實現空間位置跟蹤，然后同步路徑參數，間接協同多無人艇的速度，實現整體編隊。文獻［17］利用RBF神經網絡估計模型全局未知項和時變干擾項，設計了全驅動船舶路徑跟蹤控制器（單艘船舶控制，非編隊）。

本文采用基于領導-跟隨的目標追蹤方法。利用自適應單隱層神經網絡處理船舶模型中非線性動態和環境的時變干擾。在運動學控制中，選取跟隨船舶與參考點的偏差作為跟蹤誤差，設計運動學虛擬跟蹤控制器。利用運動學跟蹤誤差，擴展建立動力學誤差方程，并采用反步遞推技術求解出所需控制變量。可以在線學習補償非線性動態及阻尼，未建模水動力和環境干擾，控制器全局穩定且不依賴于船舶精確模型。采用一階濾波器［18］代替微分項避免了控制器反步設計的微分膨脹問題。通過解耦協調控制，只需設計單艘船舶基于領導跟隨的控制器，便可以完成編隊控制。減少了控制器設計的復雜性。

1 船舶運動模型與問題描述

1.1 運動學和動力學模型

在建立船舶運動和動力學模型時，采用隨船坐標系和大地坐標系。隨船坐標系以船舶重心為原點，船首和右舷方向為水平坐標軸。大地坐標系以正北正東方向為水平坐標軸，垂直指向地心為垂直坐標軸。本文考慮未知非線性項，給出模型詳細描述［10］。

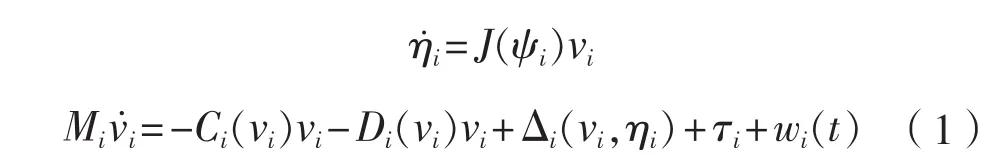
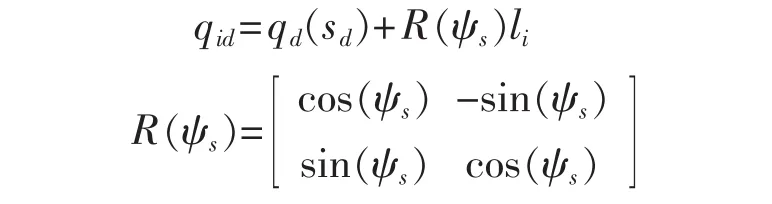
為追蹤目標點 ，定義追蹤誤差

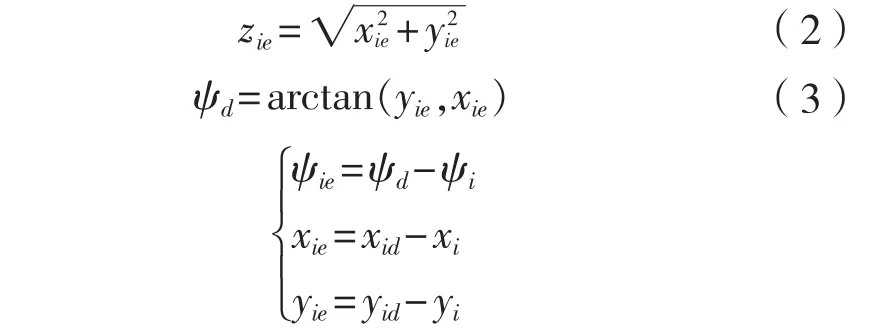
（注釋：ψd是跟隨船舶相對于目標點的角度，即跟隨船頭一直朝著目標點，控制思想是以最直接快速的方法到達目標點，沒有綜合考慮船舶的其他狀態，例如在達到追蹤點時是否速度過快，首搖角偏差是否太大，未考慮跟隨船舶的未來狀態與期望的領導船舶狀態一致。ψd采用引導船舶首搖角， 有預測控制效果，使跟隨船追蹤與引導船相同的航向。在達到追蹤點后，船舶航向與引導船航向相差無幾。）

1.2 神經網絡

采用前饋神經網絡估計不確定動態。

單隱層（SHL）網絡，輸入xk，輸出 yi，映射函數為

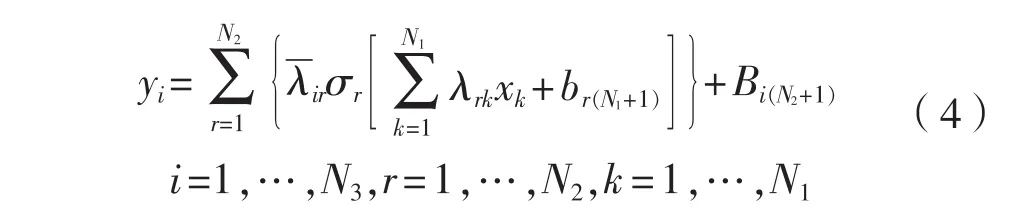
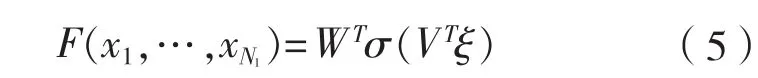
根據全局估計定理［17］，給定一個連續實函數，總存在一個理想權重矩陣使得是估計誤差，是W、V的估計值。

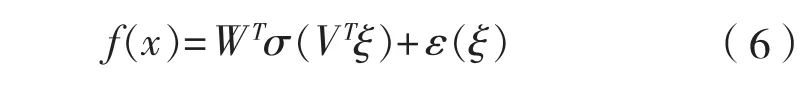
函數估計誤差：

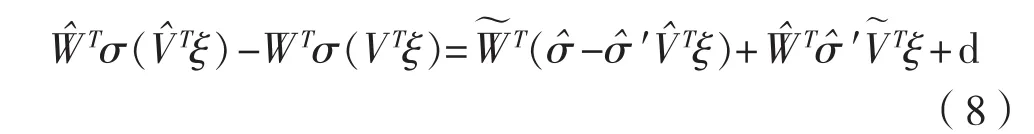
1.3 假設條件及控制目標

（1）干擾有界

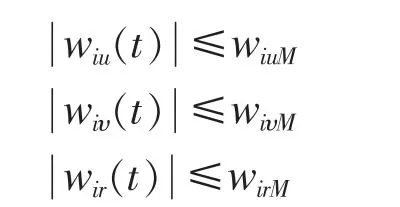
（2）橫漂速度υi無源有界

在橫向運動中，實際水動力阻尼力起主要作用，橫向速度受阻尼作用，是有界的。

（3）速度狀態可觀測

實際航行中，船舶都帶有GPS進行狀態測量，或者設計一個高增益觀測器進行估計。觀測器和控制器可以分開設計，因此假定速度可以直接測量。

控制目標是設計一個控制器，使編隊中每艘船的追蹤誤差ψis、uis、zis半全局一致最終有界。

2 控制器設計

2.1 首搖控制

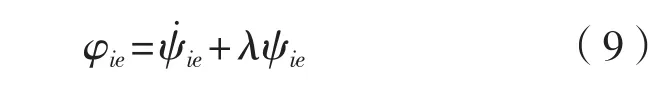
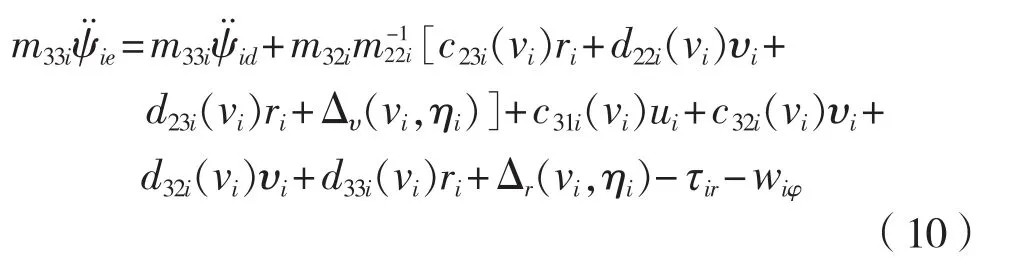
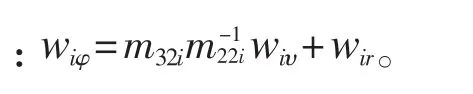
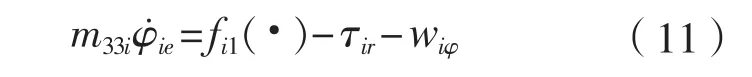
（注：直接反步法求τir，求導運算量很大，此處直接可得出τir的表達式。）未知動態函數，用神經網絡得到理論估計，為估計誤差，在具體設計中并不涉及，只用來進行穩定性分析。

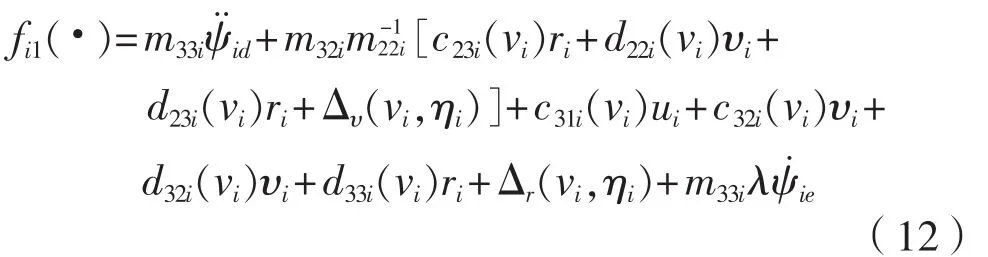
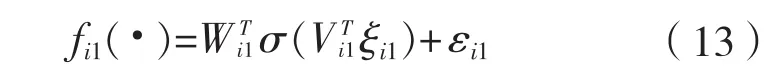
的精確表達式，用自適應項近似估計：

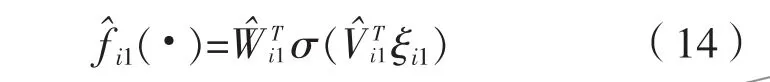
自適應率取：

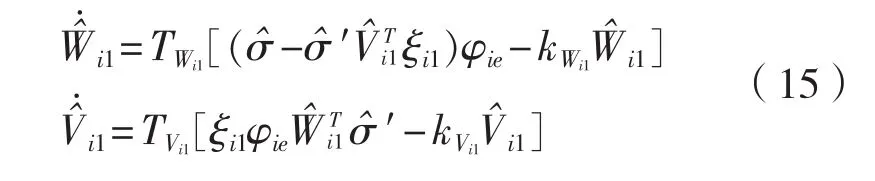
因此控制器為：

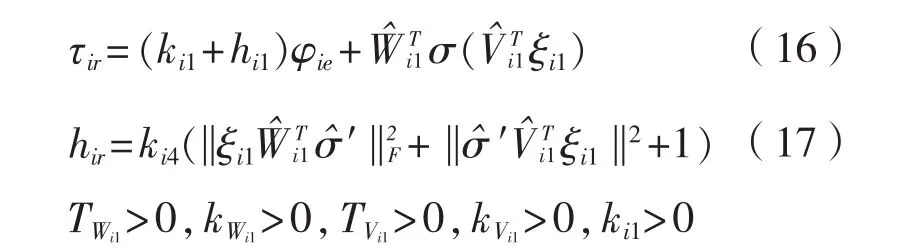
將控制項式（16）帶入式（11）得：

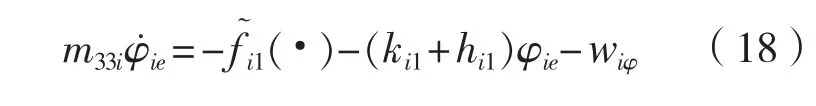
未知動態項估計誤差為：

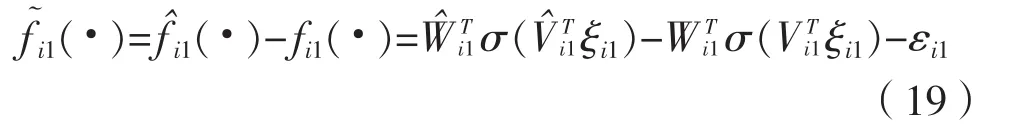
整理式（18）得：

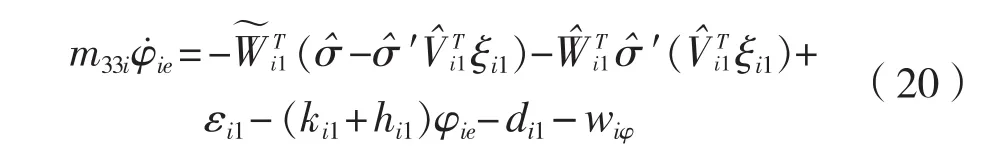
式中

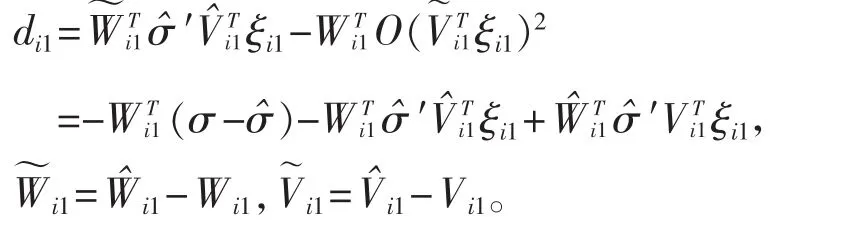
2.2 縱向控制

縱向控制直接采用反步法求出控制變量表達式。

直接求導zis，聯立（2）、（3），簡單計算整理得

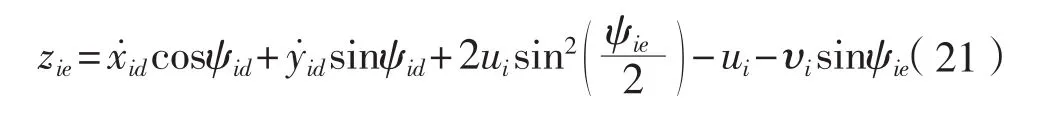
取uid為ui的虛擬控制量，定義誤差為：

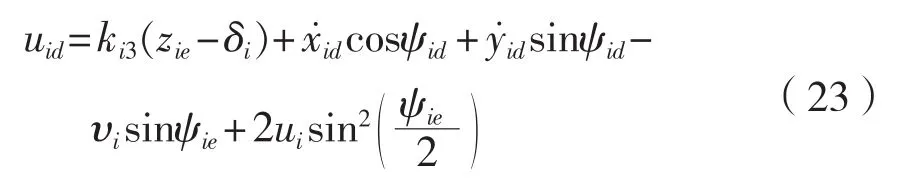
參考文獻［12］，取

對式（24）求導，結合式（21）、式（22）和式（23）得到：

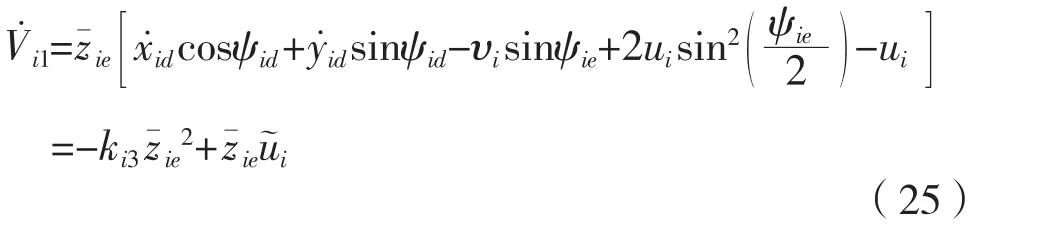
對（22）求導，結合式（1）得到：

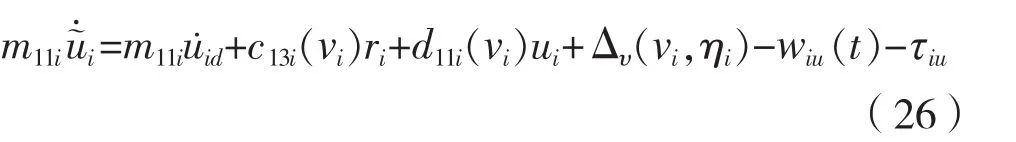
定義第2個李氏函數：

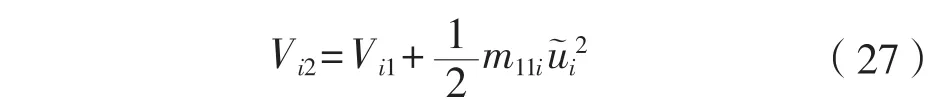
對式（27）求導，結合式（26）得：

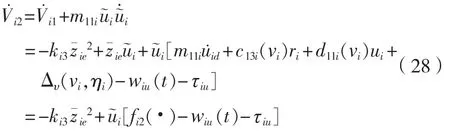
其中：

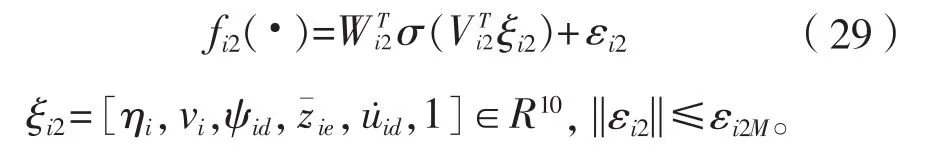
類似于式（14）取自適應項：

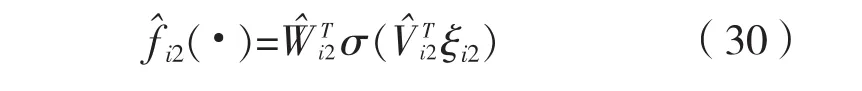
自適應率為：

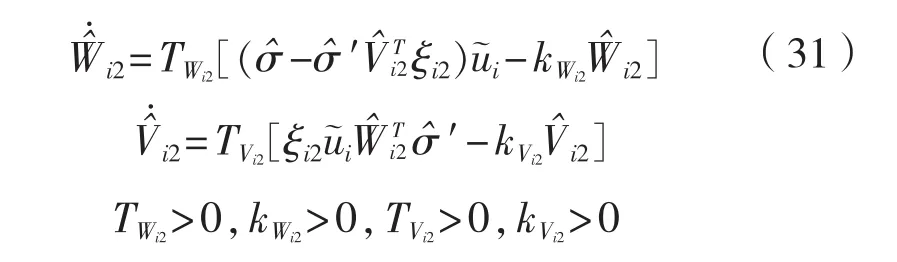
設計縱向控制器τiu：

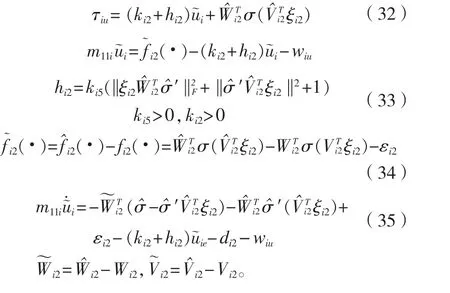
3 穩定性分析

考慮由N艘船舶組成的編隊，分析在控制器（16）、（17）、（32）、（33），自適應控制器（14）、（30）作用下閉環系統的穩定性。

證明：構造李氏函數

兩邊求導

將神經網絡權重自適應率

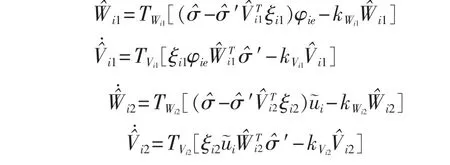
帶入，利用Young的 不等式，經整理最終得到

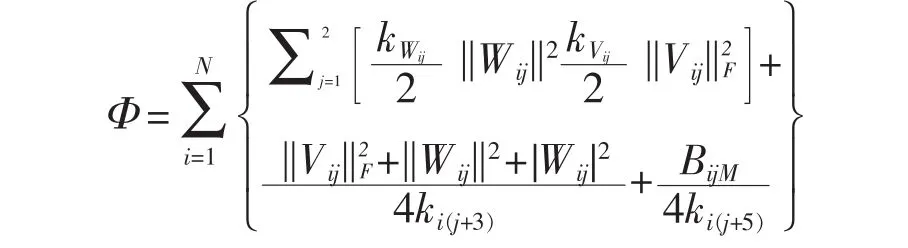
積分得

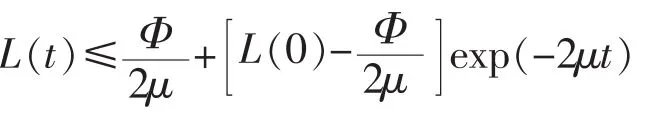
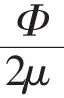
3.1 仿真驗證及分析

考慮由3艘船組成的船隊，船舶參數采用文獻［4］中的數據，船舶不確定性部分為

參見圖1，設定期望追蹤點qid與領導船位置相距2 m，即l=2。線段MVqid與MVYV夾角為30°。兩艘船舶跟蹤位置左右對稱，船舶隊形為等腰三角形。

神經網絡采用8個神經元，激活函數選擇1/［exp （-x）+1］。控制參數選取濾波器參數λ=2，ki1=10，領導船期望路徑設定為路徑隊形圖如下頁圖2所示，中間為領導船，兩側為跟隨船舶，船舶設定軌跡為圓形，隊形保持比較理想。

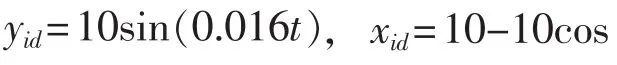
神經網絡估計動態誤差如下頁圖3所示，表明神經網絡在所設計的調整率下，能夠很好地估計未知非線性項。

圖4表明，在提出的控制器下，速度跟蹤誤差，航向角誤差，距離誤差收斂到原點的一個小的鄰域內，經仿真驗證，適當增大控制增益，誤差鄰域會進一步縮小。

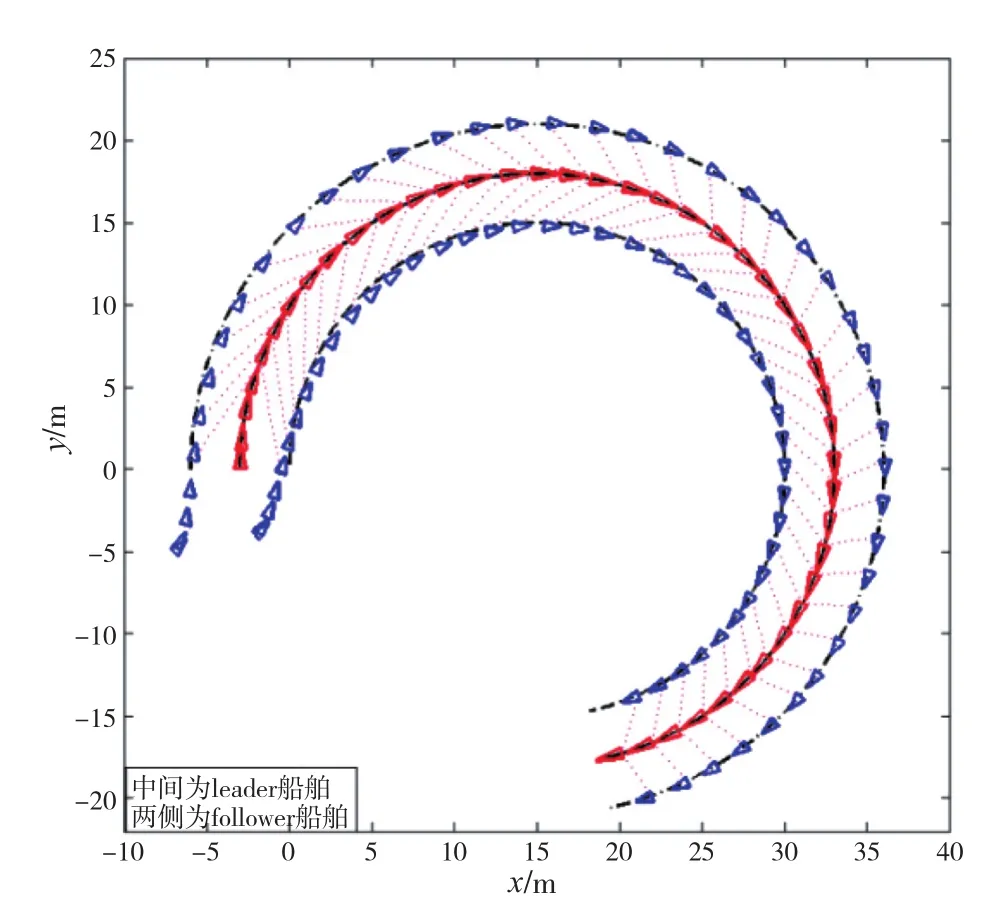
圖2　路徑隊形圖

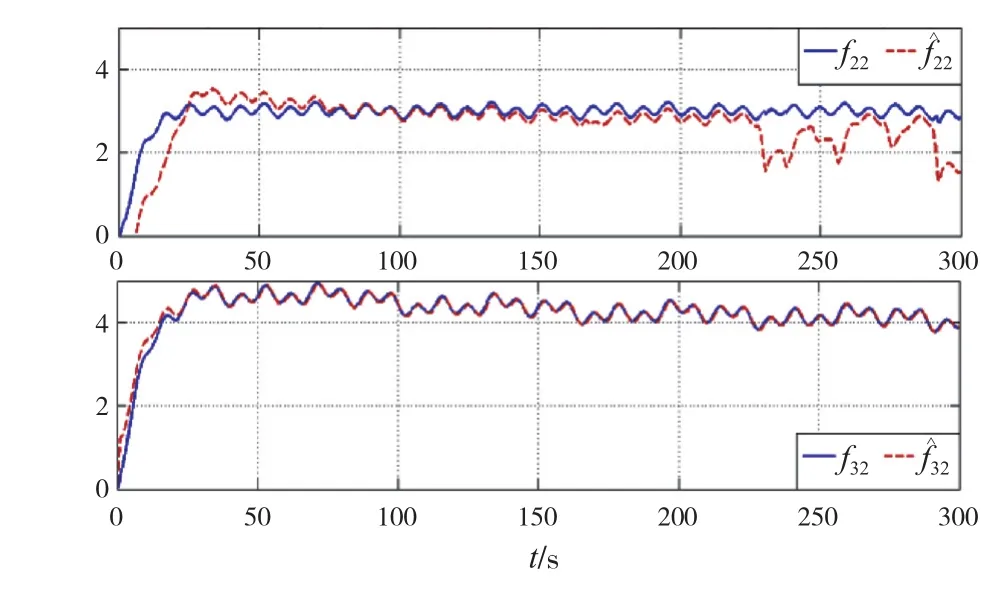
圖3　神經逼近誤差

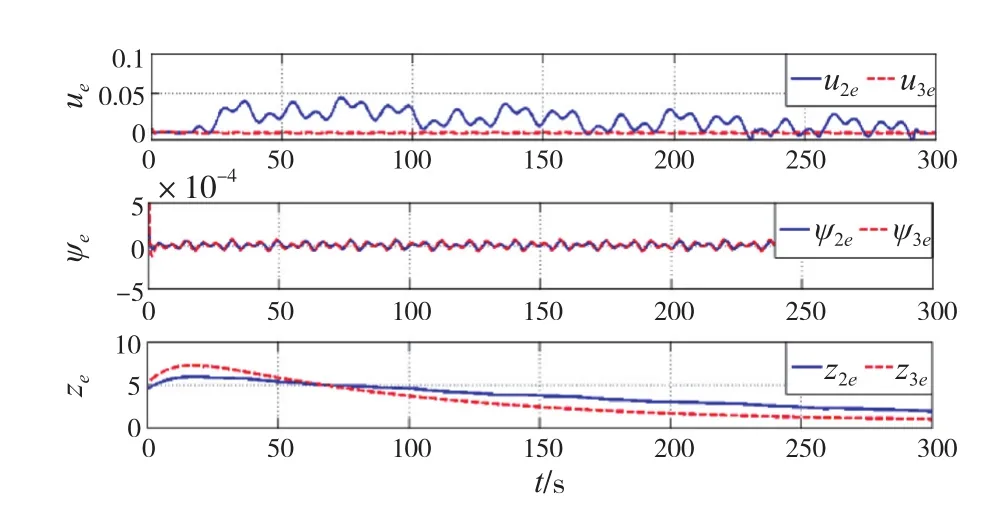
圖4　跟蹤誤差

圖5表明控制力沒有發生跳躍，并處于有界范圍內，與實際相符合。

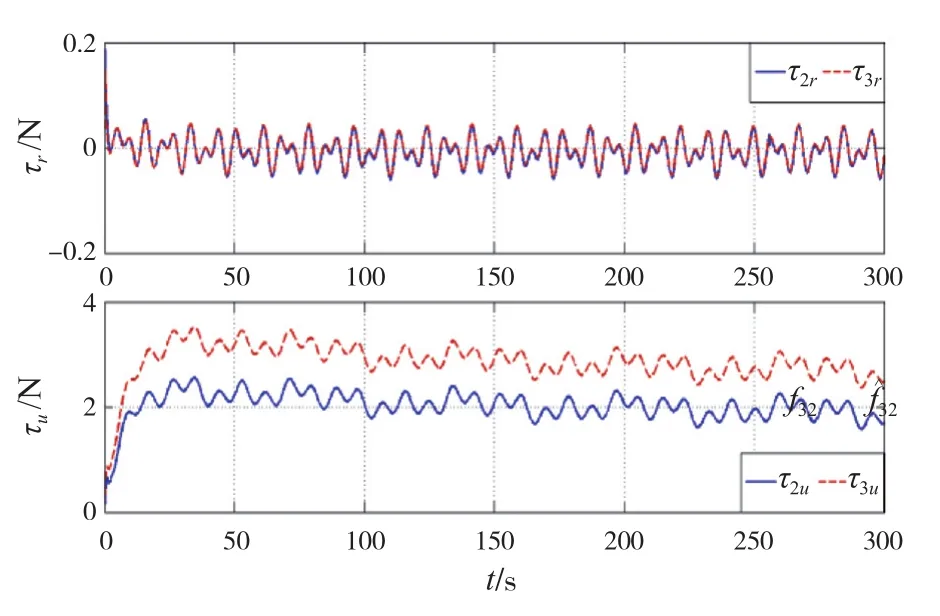
圖5　控制效果

4 結 論

本文綜合利用反步法、自適應神經網絡和動態面技術，對多艘無人艇的協同編隊控制進行研究。與基于精確模型方法相比，利用神經網絡估計補償模型中存在的非線性動態以及環境干擾等不確定性因素。針對協同編隊控制控制器結構復雜性問題，采用動態面技術代替微分項，降低了對控制器結構設計的復雜度。利用時-空解耦方法，將路徑跟蹤和引導跟隨目標跟蹤方法相結合，通過控制虛擬船參考速度間接實現了船舶編隊控制。閉環系統的李雅普諾夫分析證明系統是有界穩定的。仿真結果表明，結合神經網絡自適應控制方法的控制器是簡潔有效的。

［ 1 ］ IHLEI A F， ARCAKM， FOSSENT I. Passivity-based designs for synchronized path following， Proceedings of the 45th IEEE Conference on Decision and Control，2006，4319-4326.

［ 2 ］ BALCH T.ARKLNRC.Behavior-based formation control for multi-robot teams［J］.IEEE Transactions on Robotics and Automation，1998（6）：926-939.

［ 3 ］ 袁健，唐功友.采用一致性算法與虛擬結構的多自主水下航行器編隊控制［J］.智能系統學報，2011（3）：248-253.

［ 4 ］ Do K D.Formation control of underactuated ships with elliptical shape approximation and limited communication ranges ［J］.Automatica，2012（7）：1380-1387.

［ 5 ］ FAHIMI F. Sliding-mode formation control for underactuated surface vessels［J］.IEEE Transactions on Robotics，2007（3）：617-622.

［ 6 ］ 劉佳，陳增強，劉忠信.多智能體系統及其協同控制研究進展［J］.智能系統學報，2010（1）：1-6.

［ 7 ］ JOAO ALMEIDA，CARLOS SILVESTRE ，ANTONIO PASCOAL. Cooperative path-following of mutiple surface vessels with parameters model parametric model uncertainty and in the presence of ocean currents ［J］. International Journal of Robust and Nonlinear Control，2013（14）： 1549-1565.

［ 8 ］ BREIVIKM，HOVSTEINV.E， FOSSENT.I，Ship formation control：a guided leader-follower approach，Proceedings of the 17th IFAC World Congress，Seoul，Korea，2008.

［ 9 ］ 郭晨.欠驅動水面船舶運動控制研究綜述［J］.控制與決策，2009（3）：321-329.

［10］ Do K D，PAN J.Robust and adaptive path followingfor underactuated ships［J］. Automatica， 2004（3）：929-934.

［11］ Do K D，PAN J.Global robust adaptive path following of underactuated ships［J］.Automatica，2006（2）：1713-1722.

［12］ CUI. Leader-follower formation control of underactuated autonomous underwatervehicles［J］.Ocean Engineering，37（17/18）：1491-1502.

［13］ 李鐵山，楊鹽生，洪碧光，等.船舶航跡控制魯棒自適應模糊設計［J］.控制理論與應用，2007（3）：445-448.

［14］ WANG D，PENG Z.Robust adaptive formation control of underactuated autonomous surface vehicles with uncertain dynamics［J］.IET Control Theory and Applications，2013（12）：1378-1387.

［15］ CHEN W S， JIAOL.C.Globally stable adaptive robust tracking control using RBF neural networks as feedforward compensators， Neural Computation and Application，2010（2）：351-363.

［16］ ALMEIDA J， SILVESTREC， PASCOALA. M. Cooperative control of multiple surface vessels with discrete-time periodic communications， International Journal of Robust and NonlinearControl， 2012（3）： 398-419.

［17］ TEE，Petal K. Control of fully actuated ocean surface vessels using a class of feedforward approximators［J］. IEEE Transaction on Control System Technology，2007 （4）：750-756.

［18］ WANG D，HUANG J.Neural network-based adaptive dynamic surface control for a class of unertain nonlinear systems in strictfeedback form［J］.IEEE Transactions on Neural Networks，2005（1）：195-202.

信息動態

Ship track control based on leader-follower

QI Xiao-wei REN Guang
(Marine Engineering College, Dalian Maritime University, Dalian 116026, China)

Abstract:Cooperation formation control is very important for the unmanned surface vessels (USVs) in military and civil applications. The cooperation formation control for multiple USVs with model uncertainty and the unknown wave-current interference is achieved through the multi-agent aggregation model based on the target tracking by the leader-follower. Moreover, the unknown items and the environmental interference for the whole ship is approached through single hidden layer neural network, and the first-order filter is introduced to replace the differential items in the backstepping calculation, significantly decreasing the amount of calculation. By the timespace decoupling method, the decentralized cooperation formation control will be indirectly reached through the interactive track information for each ship. It is proved that the situation and signals of the closed-loop system are converged to a bounded set by using Lyapunov stability analysis method. The error of the control accuracy becomes arbitrarily small by selecting proper parameters. The control algorithm is then validated by the simulation results.

Keywords:unmanned surface vessel; neural network; uncertainty; multi-agent system; first-order filter; formation control

［作者簡介］齊小偉（1983-），男，碩士，研究方向：輪機工程。

［收稿日期］2015-09-07

［中圖分類號］TP273

［文獻標志碼］A

［文章編號］1001-9855（2016）01-0092-08