模糊自適應(yīng)變權(quán)重組合模型在消防中的應(yīng)用
劉洪太 郭云霞 趙剛 薛彥宇


摘 要:近年來(lái),火災(zāi)事故在我國(guó)頻頻發(fā)生,對(duì)環(huán)境和經(jīng)濟(jì)造成了巨大的影響和損失,消防應(yīng)急決策能力及決策的精確性越來(lái)越受到重視。在對(duì)火災(zāi)預(yù)測(cè)方面,組合模型較單一模型能夠更加全面準(zhǔn)確地描述火災(zāi)的變化規(guī)律。然而,組合模型中模型權(quán)重的確定主觀性太強(qiáng),影響預(yù)測(cè)結(jié)果的準(zhǔn)確性。針對(duì)上述問(wèn)題,該文提出了一種基于模糊自適應(yīng)變權(quán)重的組合預(yù)測(cè)模型,來(lái)預(yù)測(cè)火災(zāi)事故帶來(lái)的影響以及可啟動(dòng)的應(yīng)急預(yù)案等。最后,該文對(duì)提出的模型進(jìn)行了模擬應(yīng)用,預(yù)測(cè)結(jié)果準(zhǔn)確,表明該模型能夠很好地應(yīng)用于消防應(yīng)急決策,具有較高的決策價(jià)值。
關(guān)鍵詞:火災(zāi);模糊自適應(yīng);變權(quán)重;組合模型;消防應(yīng)急決策
中圖分類(lèi)號(hào):TD76 文獻(xiàn)標(biāo)志碼:A
近幾年,我國(guó)頻發(fā)火災(zāi)事故,火災(zāi)事故不僅給國(guó)家和企業(yè)帶來(lái)了財(cái)產(chǎn)、人身、生態(tài)環(huán)境上的巨大損失,甚至還會(huì)使社會(huì)動(dòng)蕩,影響社會(huì)秩序、生產(chǎn)秩序、工作秩序等。一旦火災(zāi)事故發(fā)生,決策者需要及時(shí)果斷地做出科學(xué)、合理的決策,啟動(dòng)相應(yīng)的應(yīng)急預(yù)案,最大限度地降低火災(zāi)造成的危害。目前,大數(shù)據(jù)技術(shù)及預(yù)測(cè)模型在火災(zāi)預(yù)測(cè)中得到了廣泛的應(yīng)用, 然而,大多數(shù)的研究都是基于單一的預(yù)測(cè)模型進(jìn)行火災(zāi)預(yù)測(cè),雖然一些學(xué)者也嘗試使用組合模型對(duì)火災(zāi)進(jìn)行預(yù)測(cè),但是組合模型中模型權(quán)重的確定主觀性太強(qiáng),缺少科學(xué)的方法,導(dǎo)致預(yù)測(cè)結(jié)果不準(zhǔn)確。
針對(duì)上述問(wèn)題,該文提出了一種基于模糊自適應(yīng)變權(quán)重的組合預(yù)測(cè)模型來(lái)預(yù)測(cè)火災(zāi)事故造成的損失如直接財(cái)產(chǎn)損失等。根據(jù)預(yù)測(cè)結(jié)果,應(yīng)急決策者能夠相對(duì)準(zhǔn)確及時(shí)地了解火災(zāi)事故的整體情況和可能造成的影響,快速啟動(dòng)應(yīng)急預(yù)案,極大地減少因啟動(dòng)預(yù)案延遲帶來(lái)的危害。
1 模糊自適應(yīng)變權(quán)重方法
該文使用模糊自適應(yīng)算法控制組合模型中的權(quán)重變化。對(duì)于一個(gè)組合預(yù)測(cè)模型來(lái)說(shuō),假定有n(n>2)種單一預(yù)測(cè)模型,每種預(yù)測(cè)模型都有各自的預(yù)測(cè)效果。組合模型的模糊控制因素包括在第i時(shí)刻第j種模型的誤差ej(i)和被預(yù)測(cè)對(duì)象在第i時(shí)刻的真實(shí)值相對(duì)于前面k個(gè)時(shí)刻的真實(shí)值的算術(shù)平均值的改變量cj(i),ej(i)和cj(i)的表達(dá)式分別為(1)和(2)。
1.1 模糊控制器
相對(duì)誤差ej(i)的模糊控制過(guò)程如下:
首先,將一連續(xù)區(qū)域[-1,1]分割成小的碎片,每一個(gè)碎片為一個(gè)不連續(xù)的點(diǎn),使ej(i)在[-1,1]區(qū)間內(nèi)變化,就得到了關(guān)于ej(i)的不連續(xù)區(qū)域X,稱(chēng)X為ej(i)的離散論域。使用Ak(k=1,2,…,5)來(lái)標(biāo)示相對(duì)誤差的語(yǔ)義變量,這個(gè)離散域?qū)⒈环譃?個(gè)語(yǔ)義值,見(jiàn)表1。
將E視為在i時(shí)刻第j個(gè)預(yù)測(cè)模型的預(yù)測(cè)值和在i時(shí)刻的真實(shí)值之間的誤差,用C來(lái)表示在i時(shí)刻第j個(gè)預(yù)測(cè)模型的預(yù)測(cè)值相對(duì)于在i時(shí)刻的真實(shí)值的變化率,k'j(i)表示在i時(shí)刻第j個(gè)預(yù)測(cè)模型的預(yù)測(cè)值相對(duì)于在i時(shí)刻的真實(shí)值的模糊權(quán)重。這樣,就能建立一個(gè)模糊控制規(guī)則,如下:
1.2 基于模糊自適應(yīng)變權(quán)重的組合模型
在組合模型中,如果在i時(shí)刻的實(shí)際值y(i)通過(guò)k個(gè)歷史數(shù)據(jù),從i-k時(shí)刻到i-1時(shí)刻內(nèi)的值,y(i-k),y(i-k+1),…,y(i-1)被預(yù)測(cè)出來(lái),相對(duì)于相對(duì)誤差ej(i)和灰色趨勢(shì)變量cj(i)的灰色基本權(quán)重r(ej(i))和S(c'j(i))的表達(dá)式分別為(4)和(5)。
自適應(yīng)控制系數(shù)βi的公式如(7)所示。
此外,進(jìn)行歸一化后,在i時(shí)刻,第j種預(yù)測(cè)模型的自適應(yīng)變權(quán)重kj(i)可以通過(guò)公式(8)得到。
公式(9)表示了在時(shí)刻i之前的所有時(shí)刻點(diǎn)數(shù)據(jù)對(duì)組合模型自適應(yīng)變權(quán)重全面、平均的影響。并且使用模糊自適應(yīng)變權(quán)重的方式對(duì)模型進(jìn)行組合,能夠使得個(gè)模型的權(quán)重較其他組合方法分布更合理。
當(dāng)通過(guò)歸一化Kj(i)得到在i時(shí)刻、第j種預(yù)測(cè)模型的自適應(yīng)變權(quán)重后,結(jié)合各模型模糊自適應(yīng)變權(quán)重Kj(i)和預(yù)測(cè)值fj(i),得到在i時(shí)刻的預(yù)測(cè)值,通過(guò)(9)得到:
等式(9)中,充分表明了關(guān)于模糊權(quán)重的模糊推理規(guī)則,這在模糊推理的定義過(guò)程中阻止跳躍現(xiàn)象是非常有效的。因此,這種量化方法將歸一化模糊自適應(yīng)變權(quán)重Kj(i)作為一個(gè)修正因子是相當(dāng)合理和可行的。
2 基于模糊自適應(yīng)變權(quán)重組合預(yù)測(cè)模型在消防應(yīng)急決策中的模擬應(yīng)用
2.1 模型數(shù)據(jù)選取
由于支持向量機(jī)回歸(SVMR)和徑向基函數(shù) (RBF) 神經(jīng)網(wǎng)絡(luò)具有良好的非線(xiàn)性預(yù)測(cè)控制效果,模擬應(yīng)用中使用這2種預(yù)測(cè)模型作為單一模型進(jìn)行組合預(yù)測(cè),實(shí)驗(yàn)將得出SVMR和RBF神經(jīng)網(wǎng)絡(luò)單一模型預(yù)測(cè)結(jié)果以及兩者組合模型預(yù)測(cè)結(jié)果,并進(jìn)行對(duì)比。
2.2 模型數(shù)據(jù)選取
在模擬應(yīng)用中,以某應(yīng)急管理系統(tǒng)中的火災(zāi)數(shù)據(jù)為基礎(chǔ),模擬應(yīng)用中共抽取了1 000條真實(shí)火災(zāi)記錄以及100次演練記錄作為模擬數(shù)據(jù),以數(shù)據(jù)集中前800條真實(shí)火災(zāi)事故數(shù)據(jù)和前90條演練火災(zāi)數(shù)據(jù)作為訓(xùn)練數(shù)據(jù);以數(shù)據(jù)集中后195條真實(shí)火災(zāi)事故數(shù)據(jù)和后10條演練火災(zāi)數(shù)據(jù)作為驗(yàn)證模型;以數(shù)據(jù)集中最后5條真實(shí)火災(zāi)事故數(shù)據(jù)作為測(cè)試模型,用來(lái)驗(yàn)證模型的預(yù)測(cè)性能。該文選取火災(zāi)直接財(cái)產(chǎn)損失為預(yù)測(cè)對(duì)象進(jìn)行模擬應(yīng)用。
2.3 模型權(quán)重參數(shù)
實(shí)驗(yàn)中模糊自適應(yīng)變權(quán)重方法灰色關(guān)系程度的分辨率δ取0.5,自適應(yīng)控制系數(shù)βi計(jì)算公式中,取N=0.5。
2.4 應(yīng)用效果
該文對(duì)模型預(yù)測(cè)精確性做了評(píng)估,選用平均絕對(duì)百分比誤差(MAPE)作為預(yù)測(cè)結(jié)果評(píng)判標(biāo)準(zhǔn):
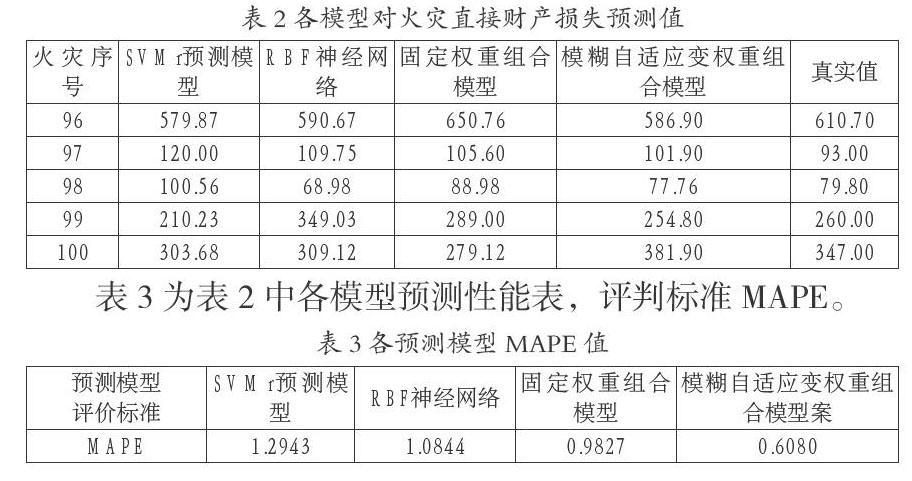
表2為使用基于模糊自適應(yīng)變權(quán)重組合預(yù)測(cè)模型與SVMr預(yù)測(cè)模型、RBF神經(jīng)網(wǎng)絡(luò)、固定權(quán)重組合模型預(yù)測(cè)最后10條真實(shí)火災(zāi)直接財(cái)產(chǎn)損失結(jié)果表。
表3為表2中各模型預(yù)測(cè)性能表,評(píng)判標(biāo)準(zhǔn)MAPE。
3.4 應(yīng)用效果分析
本模擬應(yīng)用中使用不同的預(yù)測(cè)模型對(duì)應(yīng)急系統(tǒng)中的火災(zāi)財(cái)產(chǎn)損失分別進(jìn)行了預(yù)測(cè),從3.3節(jié)中的各模型對(duì)火災(zāi)直接財(cái)產(chǎn)損失的預(yù)測(cè)值可以看出,該文提出的基于模糊自適應(yīng)變權(quán)重組合預(yù)測(cè)模型的預(yù)測(cè)相對(duì)誤差在所有模型中是最小的,雖然在極少的個(gè)別點(diǎn)上會(huì)偏大一些,但是不影響其整體性能;客觀的,從評(píng)判標(biāo)準(zhǔn)來(lái)看,該文使用的模糊自適應(yīng)變權(quán)重組合模型代表的MAPE均小于其他模型,說(shuō)明該文使用的模糊自適應(yīng)變權(quán)重組合預(yù)測(cè)模型比其他模型預(yù)測(cè)性能要好。
4 結(jié)論
該文提出了將基于模糊自適應(yīng)變權(quán)重的組合預(yù)測(cè)模型應(yīng)用于消防應(yīng)急決策,并在最后以實(shí)際的應(yīng)急系統(tǒng)進(jìn)行模擬應(yīng)用,預(yù)測(cè)效果明顯,證明了基于模糊自適應(yīng)變權(quán)重的組合預(yù)測(cè)模型能夠很好地利用火災(zāi)情景數(shù)據(jù),并獲得精確的預(yù)測(cè)效果,可以為消防應(yīng)急決策提供強(qiáng)有力的決策支持,值得推廣。
參考文獻(xiàn)
[1]傅智敏.我國(guó)火災(zāi)統(tǒng)計(jì)數(shù)據(jù)分析[J].安全與環(huán)境學(xué)報(bào),2014,14(6):341-345.
[2]張芳.消防大數(shù)據(jù)平臺(tái)的建設(shè)[J].電子技術(shù)與軟件工程,2017(7):174.
[3]趙偉,馬凱.基于灰色預(yù)測(cè)GM(1,1)模型的火災(zāi)損失預(yù)測(cè)[J].消防科學(xué)與技術(shù),2013,32(3):324-327.
[4]吳秋平.基于神經(jīng)網(wǎng)絡(luò)的森林火災(zāi)預(yù)報(bào)系統(tǒng)[J].信息化建設(shè),2016(2):26-27.
[5]張迎輝.模糊神經(jīng)網(wǎng)絡(luò)在礦井帶式輸送機(jī)火災(zāi)探測(cè)中的應(yīng)用[J].煤礦機(jī)械,2009,30(8):182-184.
[6]伍愛(ài)友,施式亮,王從陸.基于神經(jīng)網(wǎng)絡(luò)和遺傳算法的城市火災(zāi)風(fēng)險(xiǎn)評(píng)價(jià)模型[J].中國(guó)安全科學(xué)學(xué)報(bào),2006(11):108-113.
[7]袁朋偉,宋守信,董曉慶.基于灰色神經(jīng)網(wǎng)絡(luò)優(yōu)化組合模型的火災(zāi)預(yù)測(cè)研究[J].中國(guó)安全生產(chǎn)科學(xué)技術(shù),2014,10(3):119-124.
[8]唐小我,王景,曹長(zhǎng)修.一種新的模糊自適應(yīng)變權(quán)重組合預(yù)測(cè)算法[J].電子科技大學(xué)學(xué)報(bào),1997(3):66-69.
[9]張曉輝,常淑惠,張璠,等.支持向量機(jī)的基本理論與應(yīng)用[J].科技經(jīng)濟(jì)導(dǎo)刊,2017(5):32,17.
[10]衛(wèi)敏,余樂(lè)安.具有最優(yōu)學(xué)習(xí)率的RBF神經(jīng)網(wǎng)絡(luò)及其應(yīng)用[J].管理科學(xué)學(xué)報(bào),2012,15(4):50-57.

