基于在線測量的滾動直線導軌副精度保持性測試方法及試驗研究

姬中晴， 歐　屹， 馮虎田， 張　云

(南京理工大學 機械工程學院，南京　210094)

?

基于在線測量的滾動直線導軌副精度保持性測試方法及試驗研究

姬中晴， 歐屹， 馮虎田， 張云

(南京理工大學 機械工程學院，南京210094)

摘要：針對滾動直線導軌副精度保持性檢測要求，提出了一種基于激光位移傳感器測距的滾動直線導軌副運動精度在線檢測方法。根據相對運動定理，該方法將4個激光位移傳感器在線測量的滑塊相對導軌基準的距離變化量轉化成導軌平行度和滑塊偏轉角的變化量。通過滾動直線導軌副精度保持性測試方法，在線測量滾動直線導軌副在實際運行過程中的精度損失量，并與滾動直線導軌副的離線數據對比，有效驗證了測試原理的可行性。隨后，從多方面進行了誤差分析。

關鍵詞：滾動直線導軌副；精度保持性；試驗研究；在線測量

滾動直線導軌副具有定位精度高，摩擦阻力小，裝配簡單、壽命長等優點而廣泛應用于專用機床、數控機床和加工中心等設備，已成為精密數控設備的關鍵功能部件[1]。滾動直線導軌副精度可靠性的衡量標準為精度保持性。精度保持性是指滾動直線導軌副在規定條件下和規定時間內精度保持在某一范圍而不喪失的能力[2]，是評價機床中使用滾動直線導軌副可靠性的重要指標，也是國內產品與國外產品重要差距所在。所以，從提高國內滾動直線導軌副的產品性能出發，很有必要對滾動直線導軌副的精度保持性測試理論和方法進行研究。

滾動直線導軌副精度的檢測方法主要有手動測量和自動化測量兩種。傳統的測量方法以手動離線測量為主，但離線測量具有一定的局限性，首先它是靜態測量，不能描述導軌工作時的精度損失特性。其次，不能確保工作和測量時導軌能在同一基準下進行精度損失的檢測。目前我國導軌精度保持性自動化檢測裝備的研究比較滯后，一般自動化檢測只是一種檢測裝置，不能在同一基準下模擬實際工況進行精度保持性試驗和檢測。

本文提出了一種基于使用激光位移傳感器進行在線測量的精度保持性試驗方法，用于描述和檢測滾動直線導軌副運動精度的變化。通過一組激光位移傳感器相對基準面距離的實時測量數據，得出滑塊中心在運動過程中的平行度和偏轉角變化量，解決了滾動直線導軌副在線測量的難題，為開展精度保持性試驗提供了測試依據。同時開展了大量對比驗證試驗，證明了本方法的可行性與準確度。

1滾動直線導軌副精度保持性試驗裝置

精度保持性試驗及在線檢測方法基于南京理工大學自主研發的滾動直線導軌副精度保持性試驗臺，該試驗臺能夠在模擬實際工況的條件下進行精度保持性試驗[3]。試驗裝置見圖1。

圖1　滾動直線導軌副精度保持性試驗臺Fig.1 The test bench of linear rolling guide movement precisiontest-bed

試驗臺激光位移傳感器安裝方式見圖2。傳感器1、傳感器2對稱分布于滑塊側面兩端，測量滑塊側面相對導軌同側側面基準的平行度以及滑塊相對導軌的偏擺角變化量；傳感器3、傳感器4對稱分布于滑塊頂面中心處兩側，測量滑塊頂面相對導軌底面基準的平行度以及滑塊相對導軌的俯仰角變化量。

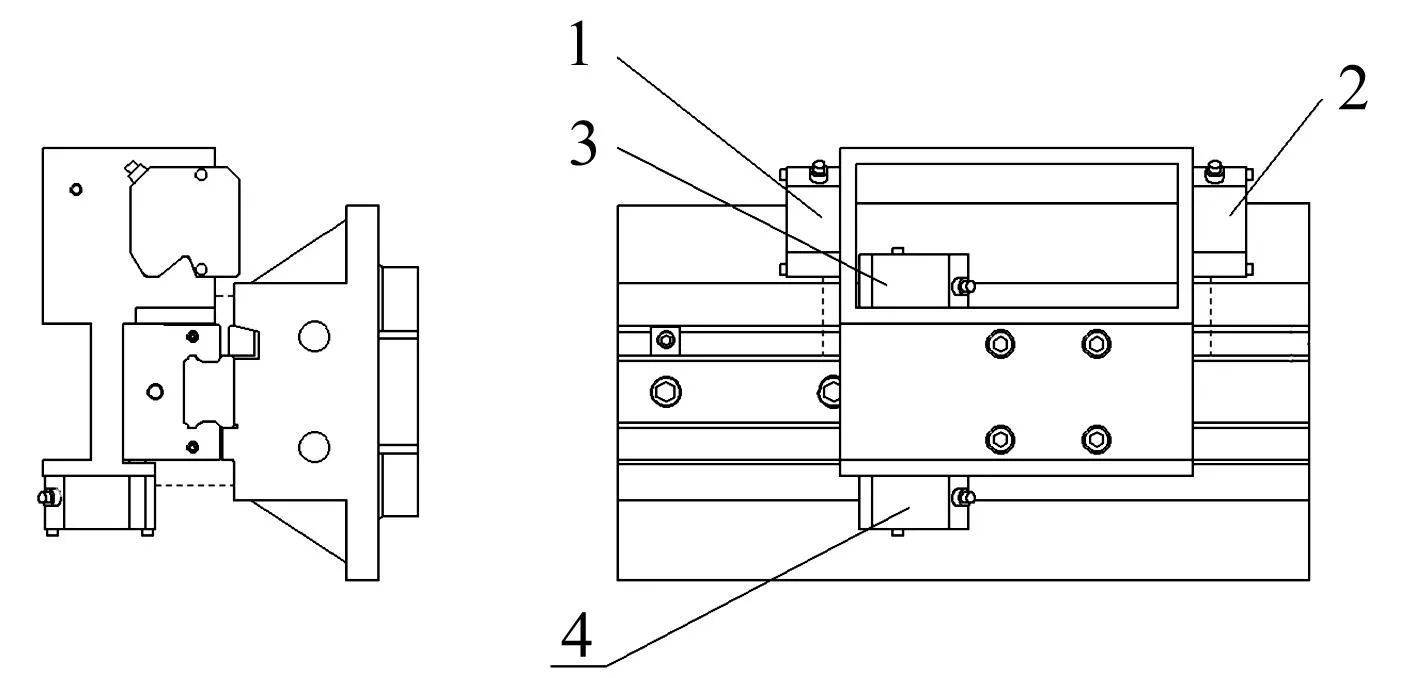
圖2　激光位移傳感器安裝圖Fig.2 Installation diagram of laser displacement sensor

2滾動直線導軌副精度檢測方法

2.1滾動直線導軌副精度的離線檢測方法

滑塊移動對導軌的平行度是滾動直線導軌運動精度的具體指標。根據滾動直線導軌副驗收技術條件，精度的離線檢測主要包括：① 滑塊移動對導軌底面基準A的平行度；② 滑塊移動對導軌側面基準B的平行度[4]。具體檢測方法見圖3。

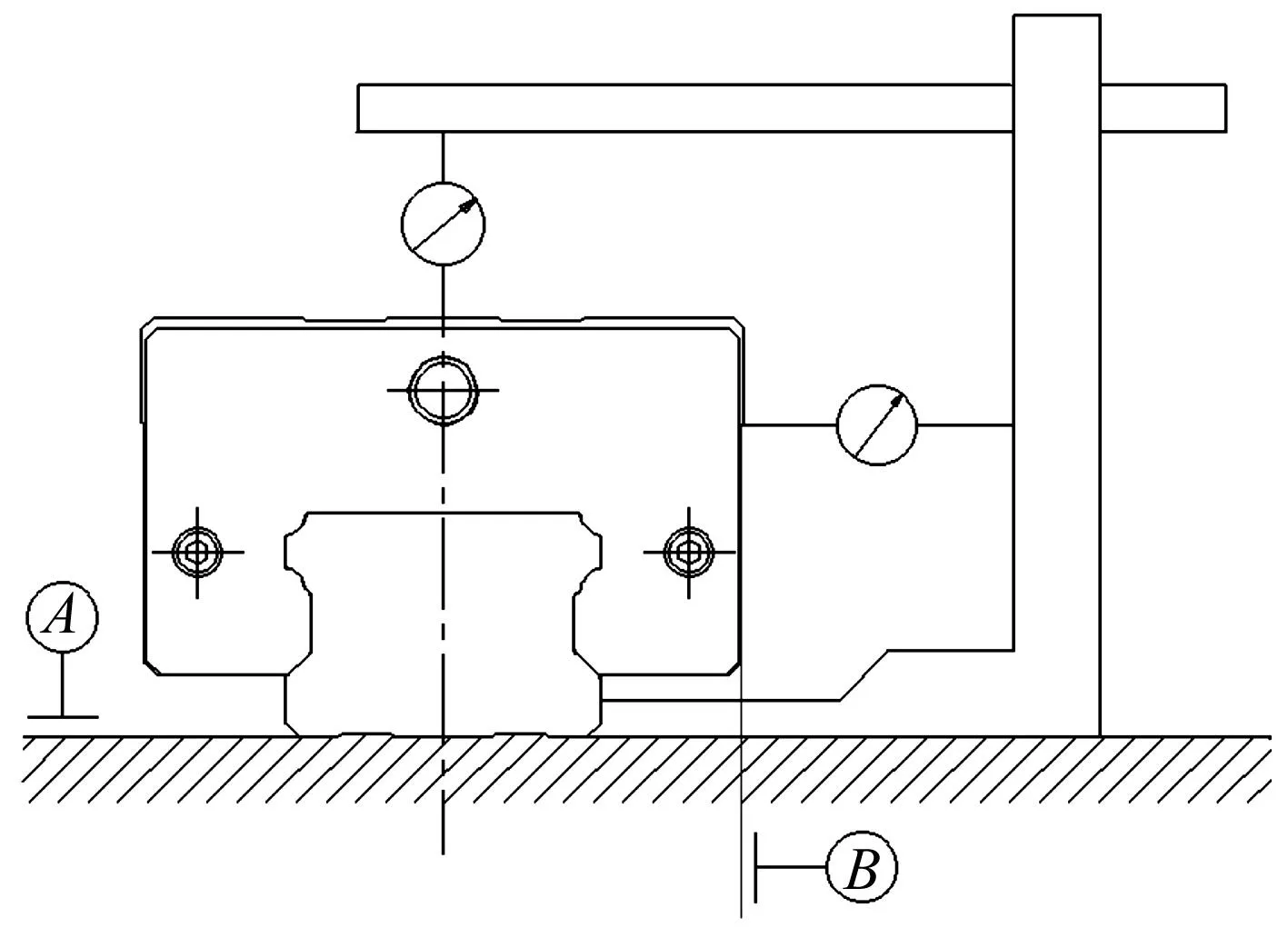
圖3　導軌離線測量原理圖Fig.3 Schematic diagram of the guide off-line measurement

這種傳統的導軌精度離線檢測方法較之在線檢測有以下不足：① 離線檢測為靜態手動測量，不能實時監測導軌正常工作時的運動精度損失情況；② 每次離線測量必須放在專門的高平面度檢測臺上，拆裝困難，檢測效率低。③ 導軌工作時的安裝基準和檢測臺基準不能確保基準的同一性。

2.2滾動直線導軌副精度的在線檢測方法

滾動直線導軌副在使用一定時間后，導軌、滑塊及滾動體之間會產生接觸變形和磨損，導致滾動體接觸角改變及滑塊位移。滾動直線導軌副精度保持性試驗臺可在線檢測滑塊移動對基準面的平行度以及滑塊相對導軌的偏轉角度變化量。

設定滑塊在導軌最左端時的幾何中心為原點O，分別以垂直滑塊側面、頂面、端面為X、Y、Z軸建立基準坐標系O-XYZ。滑塊運動了任意距離L后，坐標系為O′-X′Y′Z′(見圖4)。

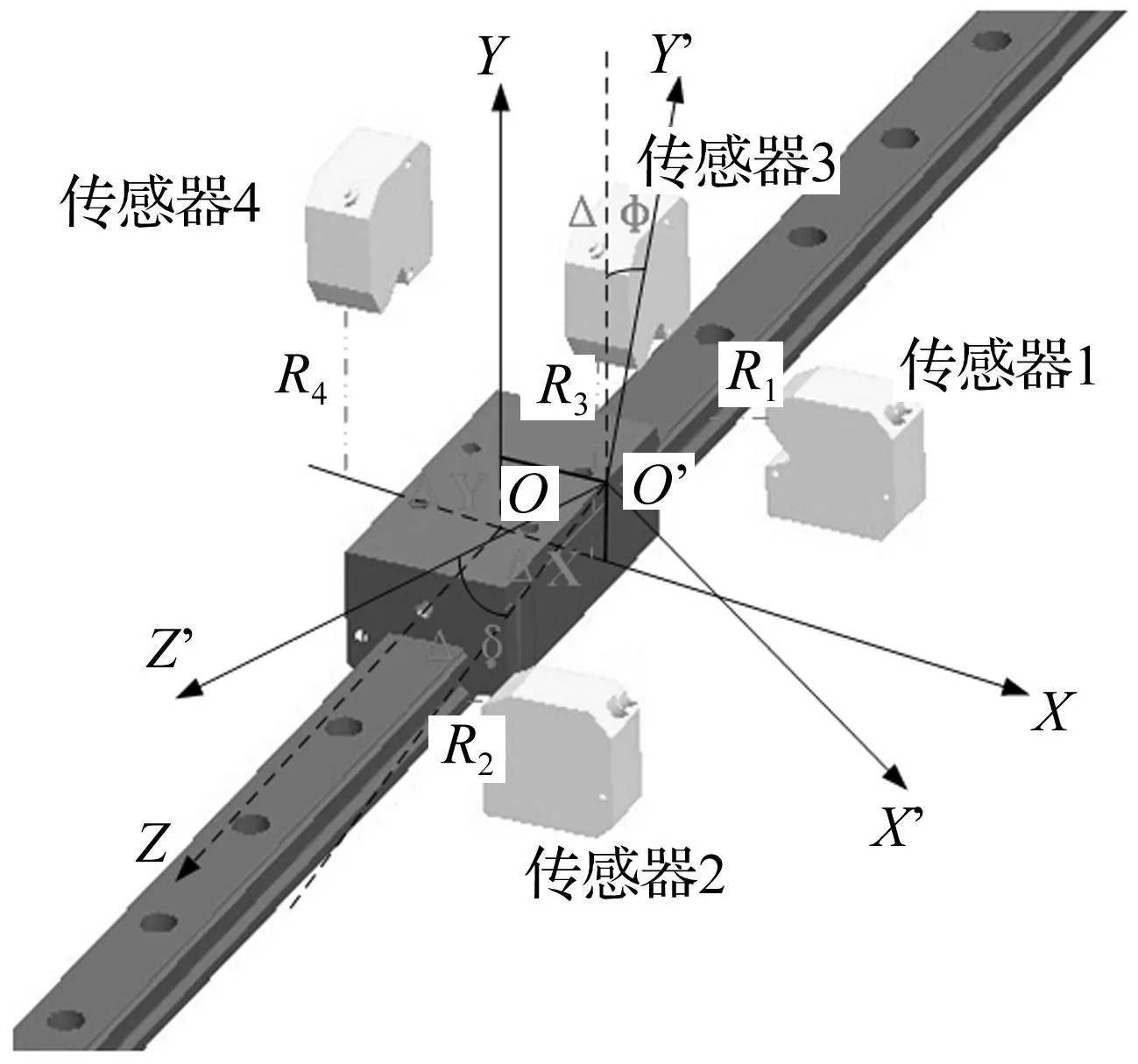
圖4　滾動直線導軌副坐標系Fig.4 The linear rolling guide coordinate system

滑塊在運動過程中基準坐標系在X軸和Y軸方向有偏移，并繞Y軸和Z軸產生偏轉。根據精度的檢測方法，在X軸和Y軸的偏移量ΔX、ΔY即為側面平行度和頂面平行度的變化量，在導軌全長上測得的ΔX、ΔY中，最大的變化量maxΔX和maxΔY即分別為滑塊側面對導軌同側側面基準的平行度、滑塊頂面對導軌底面基準的平行度。滑塊端面繞Y軸的偏擺角Δδ為滑塊相對導軌的偏擺角變化量；滑塊頂面繞Z軸的翻轉角ΔΦ為滑塊相對導軌的俯仰角變化量。

2.2.1偏轉角和俯仰角的計算

測量偏擺角的變化量時，假設滑塊相對導軌先發生俯仰變化，再發生偏擺。根據相對運動定理，將滑塊視為定物，導軌基準側面相對滑塊進行俯仰和偏擺(見圖5)。滑塊俯仰后，傳感器1、傳感器2示數以相同大小增加或減小X；滑塊偏擺后，傳感器1、傳感器2示數發生變化。偏擺角變化量的正切函數等于其示數差與其安裝距離之比，如式(1)所示：

(1)

式中：R1、R2為位移傳感器1、傳感器2到對應基準面的初始距離；R1′、R2′為位移傳感器1、傳感器2到對應基準面的實際距離；L(1-2)為位移傳感器1、傳感器2激光間距。

圖5　滑塊側面相對導軌先俯仰后偏擺示意圖Fig.5 Schematic diagram that the slider side relative to the yaw after pitch of guide

假設滑塊相對導軌先發生偏擺，隨后發生俯仰(見圖6)。則其偏擺角的變化量如式(2)所示：

(2)

圖6　滑塊側面相對導軌先偏擺后俯仰示意圖Fig.6 Schematic diagram that the slider side relative to the pitch after yaw of guide

由式(1)和式(2)可知，在建立滑塊相對導軌的旋轉模型時，其偏擺與俯仰的順序不影響偏擺角的計算。

測量俯仰角的變化量時，假設滑塊相對導軌先發生偏擺變化，再發生俯仰。根據相對運動定理，將滑塊視為定物，導軌基準底面相對滑塊進行偏擺和俯仰(見圖7)。滑塊偏擺后，由基準面1變為基準面2，傳感器3、傳感器4示數不變；滑塊俯仰后，由基準面2變為基準面3，傳感器3、傳感器4示數發生變化。俯仰角變化量的正切函數等于其示數差與其安裝距離之比，如式(3)所示：

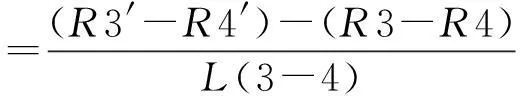
(3)

式中：R3、R4為位移傳感器3、傳感器4到對應基準面的初始距離；R3′、R4′為位移傳感器3、傳感器4到對應基準面的實際距離；L(3-4)為位移傳感器3、傳感器4激光間距。

圖7　滑塊頂面相對導軌先偏擺后俯仰示意圖Fig.7 Schematic diagram of the slider top surface relative to the pitch after yaw of guide

假設滑塊相對導軌先發生俯仰，隨后發生偏擺(見圖8)。滑塊俯仰后，由基準面1變為基準面2，傳感器3、傳感器4示數變化；滑塊偏擺后，由基準面2變為基準面3，傳感器3、傳感器4示數不變。其偏擺角的變化量如式(4)所示：

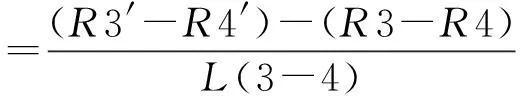
(4)

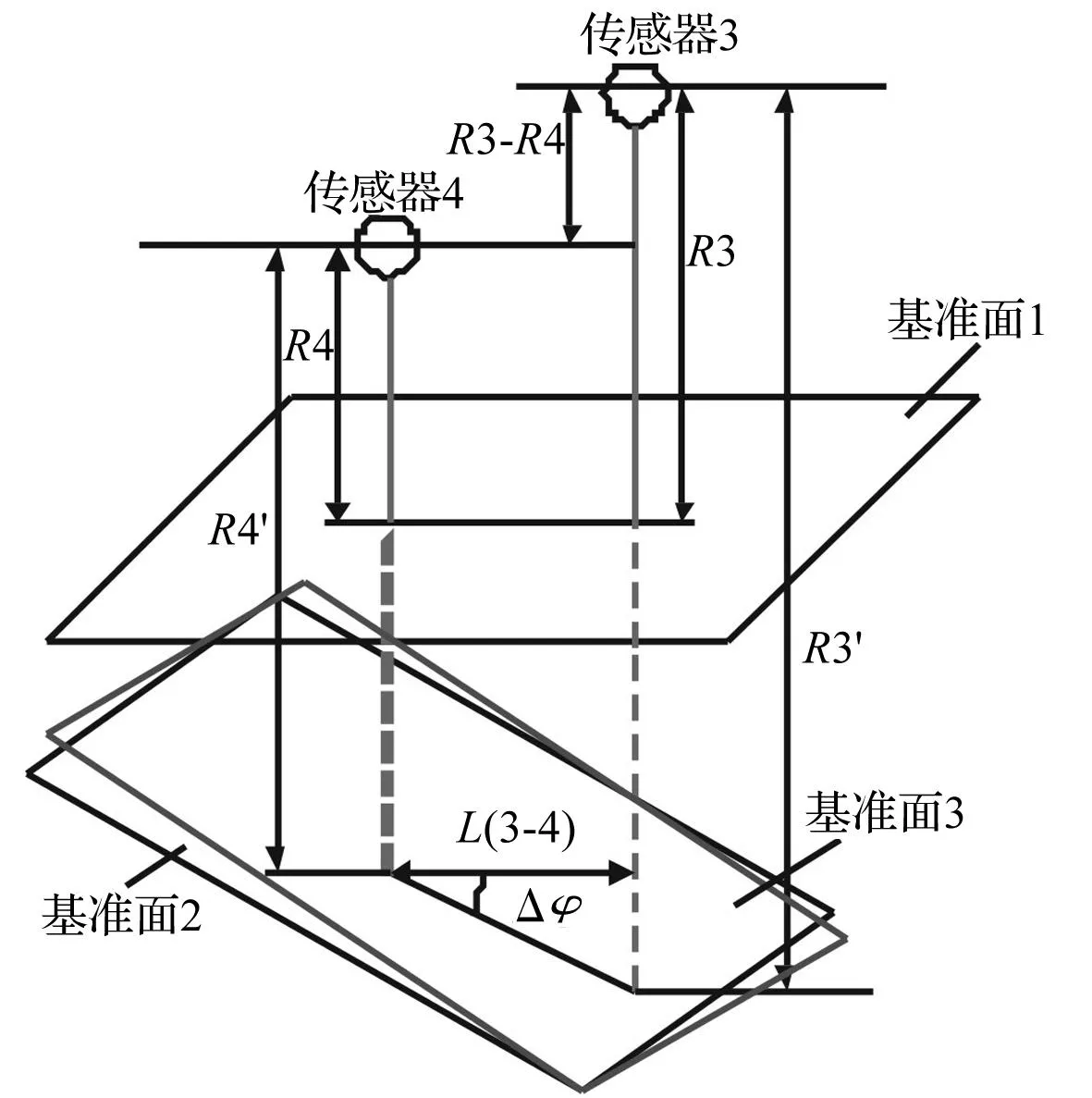
圖8　滑塊頂面相對導軌先俯仰后偏擺示意圖Fig.8 Schematic diagram of the slider top surface relative to the yaw after pitch of guide

由式(3)和式(4)可知，在建立滑塊相對導軌的旋轉模型時，其偏擺與俯仰的順序不影響俯仰角的計算。

2.2.2平行度和精度損失的計算

根據平行度定義將傳感器采集數據進行換算，得到滑塊頂面中心處及滑塊側面中心處的平行度。

由圖9可知，滑塊側面中心處在X軸方向的偏移量ΔX可根據下式計算：

(5)

式中：δ為傳感器1、2在Z軸方向的初始角度，其大小如下：

(6)

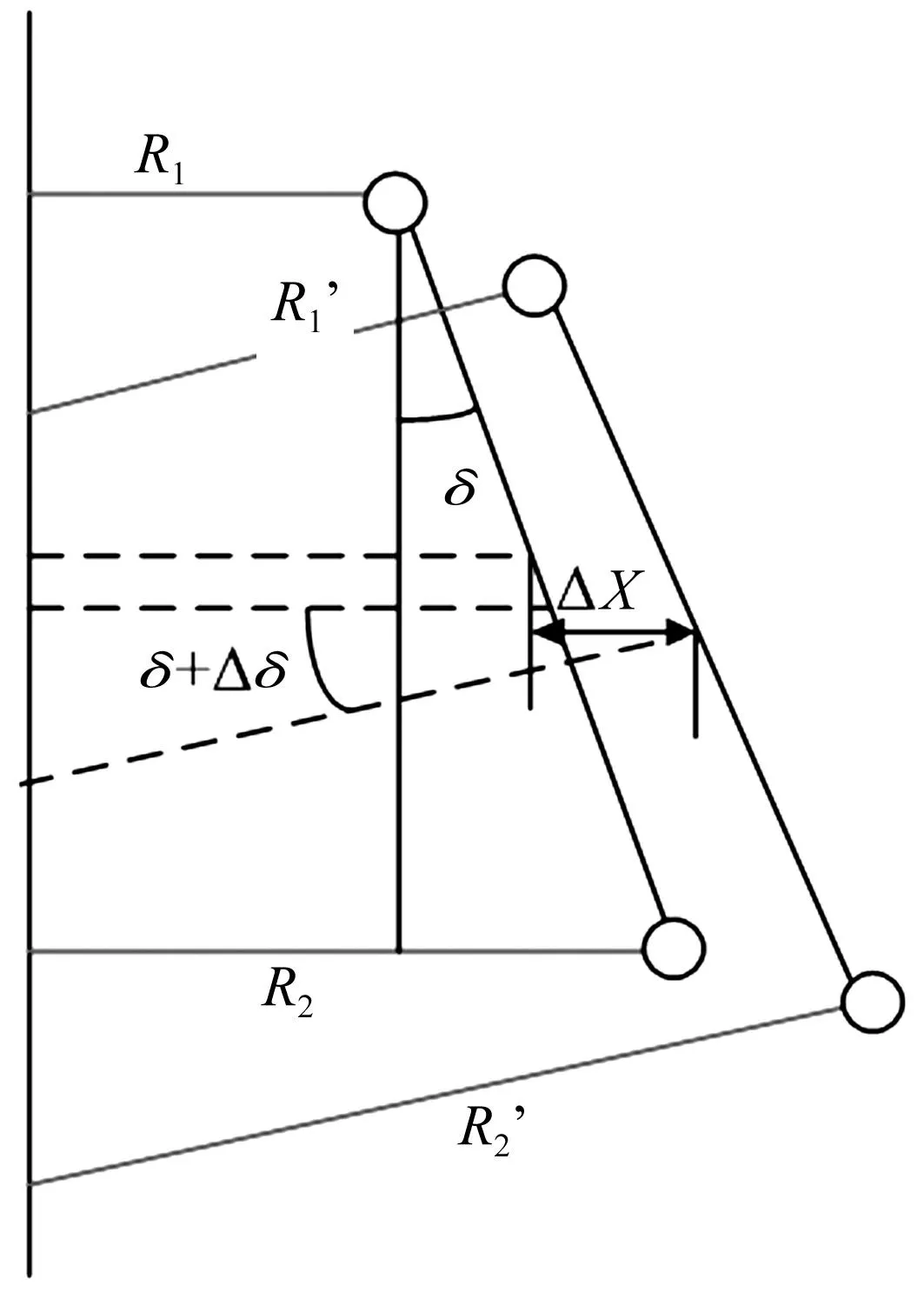
圖9　側面平行度變化量ΔX計算模型Fig.9 The computational model of side Parallelism’s change ΔX

由圖10可知，滑塊頂面中心處在Y軸方向的偏移量ΔY可根據下式計算：

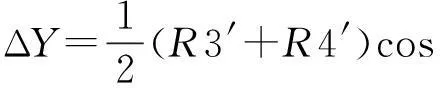
(7)

式中：Φ為傳感器3、傳感器4在X軸方向的初始角度，其大小如下：

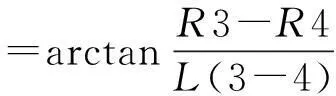
(8)

圖10　頂面平行度變化量ΔY計算模型Fig.10 The computational model of top Parallelism’s change ΔY

由式(5)、式(6)，可得滑塊側面相對導軌同側側面基準的平行度變化量ΔX；由式(7)、式(8)，可得滑塊頂面相對導軌底面基準的平行度變化量ΔY。以上模型均適用于基準面為絕對平面時的計算。

在實際測量過程中，由于傳感器1、傳感器2的激光打在導軌側面基準上，導軌側面基準可近似認為是相對平面，因此在測量的ΔX(j)中，取其最大值與最小值之差即為檢測的側面平行度。第一次檢測的平行度為maxΔX1，第i次檢測的平行度為maxΔXi，從第一次檢測到第i次檢測的精度損失量為(maxΔXi-maxΔX1),見圖11。

圖11　導軌側面測量原理示意圖Fig.11 Schematic diagram of the side measuring principle for the guide

傳感器3、傳感器4的激光打在導軌轉接板基準面上，經檢測，該轉接板的基準面并不是一個絕對平面，其誤差相對導軌平行度不容忽略。因此，需對檢測的數據進行一定的處理，以得到滑塊頂面相對導軌底面基準的平行度。假設第一次檢測得到相應點的ΔY為ΔY1(j)，第i次檢測得到相應點的ΔY為ΔYi(j)見圖12。當檢測次數i≥2時，檢測時需減去對應點的第一次檢測值，得到相對第一次檢測的一系列差值{ΔYi(j)-ΔY1(j)}，其中i=0,1,2,3,…;j=0，1,2,3,…。假設其最大值為maxΔYi，最小值為minΔYi，則從第一次檢測到第i次檢測的精度損失量為(maxΔYi-minΔYi)。

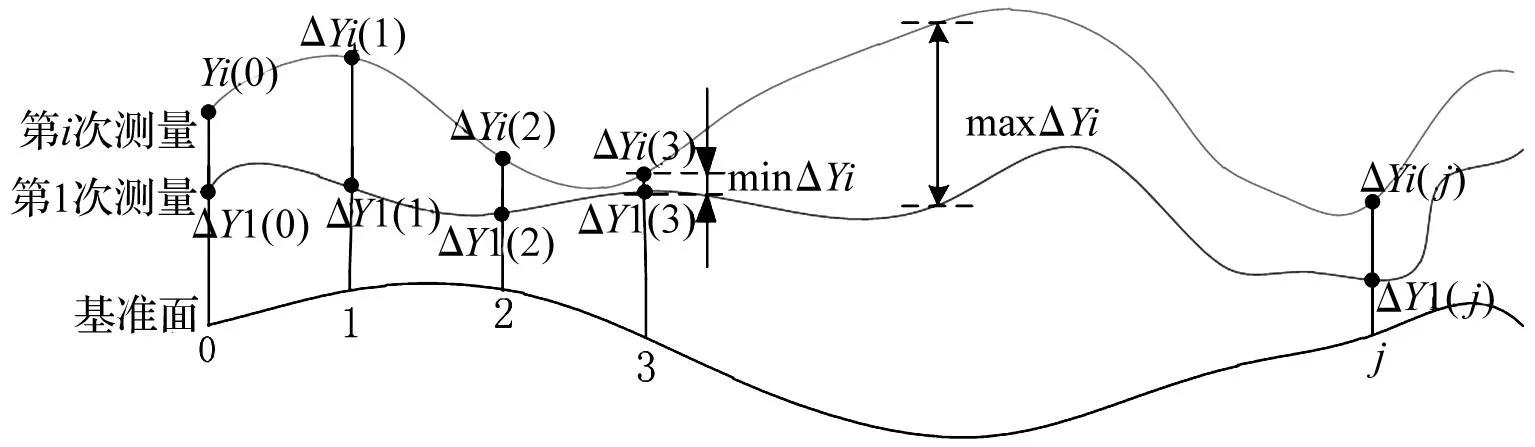
圖12　導軌底面測量原理示意圖Fig.12 Schematic diagram of the underside measuring principle of guide

3滾動直線導軌副精度保持性試驗研究

3.1滾動直線導軌副精度保持性試驗分析

滾動直線導軌副精度保持性指標用有效精度保持時間或磨損壽命表示，對于一批產品用磨損壽命可靠度表示[5]。有效精度保持時間是指在規定條件下導軌精度保持在規定的等級范圍內而未喪失的時間。磨損壽命可靠度是指在規定條件下一批導軌有效精度保持時間為某一特定值的概率。

精度儲備量Ec是指被測滾動直線導軌副樣品的標稱精度允許值與離線測量實際值的差值[6]，隨著導軌在運行時間的增大，滾道與滾珠的磨損會增大，精度損失也會越來越大。

在試驗中，當被測樣品的運動平行度損失值≥80%Ec時，應停止試驗并離線測量。若精度未失效，則計算出新的儲備量并繼續進行試驗。精度保持性測試原理見圖13。

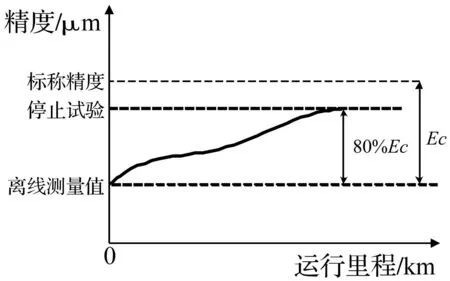
圖13　精度保持性測試原理圖Fig.13 Schematic diagram of movement precision measurement

3.2滾動直線導軌副精度保持性試驗

應用以上測量原理，采用國內廠家3級3 000 mm長的導軌在滾動直線導軌副精度保持性試驗臺上進行試驗。根據滾動直線導軌副第四部分驗收技術條件[4]，該導軌的頂面與側面精度離線測量值分別為12 μm和14 μm，標稱精度允許值都為20 μm，因此，頂面精度儲備量Ec1=8 μm，側面精度儲備量Ec2=6 μm。圖14為激光位移傳感器安裝實物圖。

圖14　激光位移傳感器安裝實物圖Fig.14 Installation physical diagram of laser displacement sensor

精度保持性試驗方案采用滾動功能部件行業標準進行試驗和測量[6]，在線測試結果見圖15和圖16。

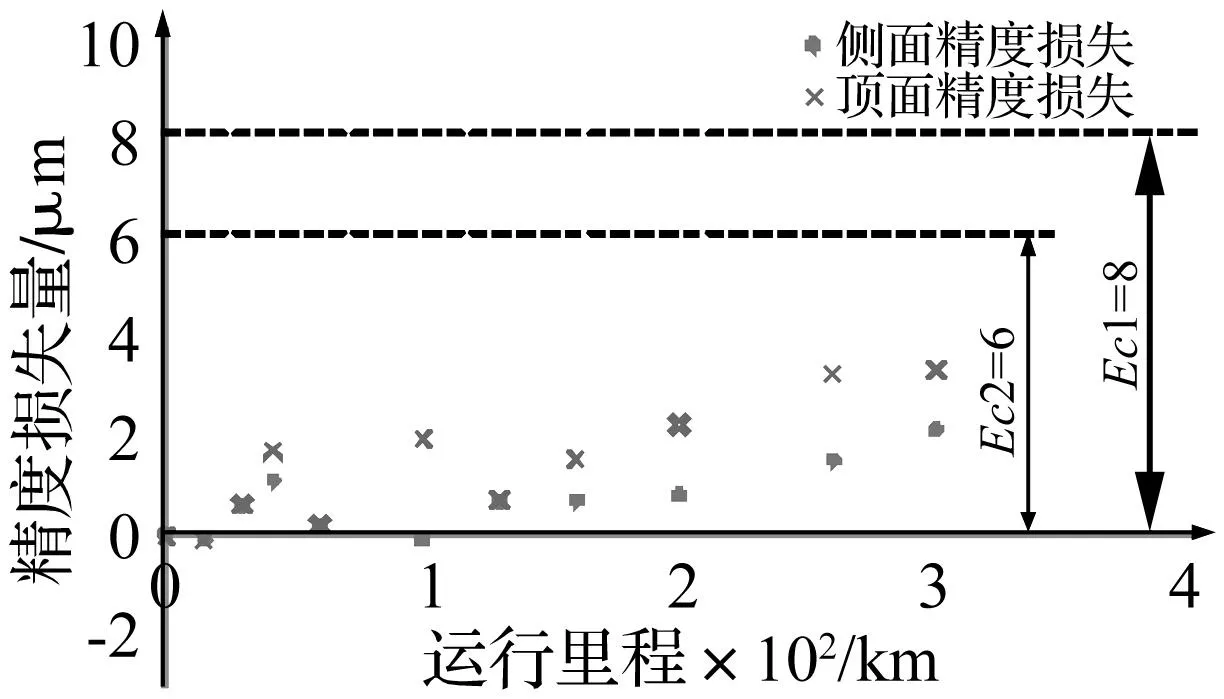
圖15　精度保持性精度損失測試結果Fig.15 The Loss of accuracy measurement result of movement precision

圖16　精度保持性滑塊偏轉角測試結果Fig.16 The measurement result of slider deflection angle ofmovement precision

直線導軌的運行是一個磨損過程，其過程可以分為磨合階段、穩定磨損階段和急劇磨損階段。從圖16可知，離散數據可以看出隨著運行里程的增加，精度損失呈增大趨勢。在運行初期，導軌處于磨合過程而出現了一定的波動。屠國俊在試驗和論文中也曾表述過這種現象。這說明導軌初期確實存在磨合過程，出現波動現象與實際情況相一致。為了驗證測試原理，將導軌300 km時的精度損失量在線測量值與離線測量值進行對比。

由表1可見，在線檢測與離線檢測所得的精度損失值相差微小，從而驗證了在線檢測方法的可行性。由于滾珠直線導軌本身壽命較高，試驗耗費的時間長，到截稿時試驗仍在繼續，所以只選取導軌運行300 km時的數據。

表1　精度保持性離線與在線測試結果對比表

4數據誤差分析

4.1算法誤差

對于滾動直線導軌副，滑塊在運動的過程中會

產生俯仰和偏擺。根據布爾沙-沃爾夫模型[7-8]，在滑塊在導軌最左側建立基準坐標系O-XYZ，滑塊運動到任意位置時的坐標系為O′-X′Y′Z′，Y軸與Y′軸的夾角即為俯仰角，Z軸與Z′軸的夾角即為偏擺角。在數據處理中，計算側面平行度時忽略了俯仰角的變化，計算頂面平行度時忽略了偏擺角的變化。由于試驗中測得的初始偏轉角的角度約為2°×10-3，幾乎不影響平行度的測量，因此這個誤差可以忽略。

4.2傳感器精度誤差

滾動直線導軌副精度保持性試驗臺的精度檢測采用的激光位移傳感器，測量范圍為±10 mm，線性誤差為±4 μm。因此，傳感器本身測量的時候會帶來一定的誤差。

4.3安裝誤差

安裝誤差對運動精度有比較大的影響，滑塊頂面的精度損失是由傳感器測量的導軌轉接板平面的相對距離得出。雖然該平面與導軌的安裝基準底面采用同一道工序加工而成，保證兩個平面具有相同的尺寸、表面粗糙度和形位公差，但在安裝被測導軌的時候，不能保證兩個平面完全平行，因此會給精度檢測帶來一定的誤差。但是，根據文中提到的計算方法，采用對應數據相減得到精度損失量，可以抵消由于安裝和基準問題產生的誤差。因此，忽略長時間運行床身蠕變可能因素的影響，安裝誤差對精度保持性試驗的影響幾乎可以忽略。

4.4其他誤差

由滾動直線導軌副精度保持性試驗規范可知，潤滑油中灰塵及機械雜質的顆粒不應大于10 μm。但被測導軌副處于開放式環境中，潤滑油、空氣中難免會有雜質顆粒[9]，因此會給精度測量帶來必然的不確定的誤差。此外，導軌副的預加載荷和測試速度對導軌副的運動精度有一定影響[10-11]。

5結論

本文通過分析滾動直線導軌副精度保持性試驗臺的結構特性，研究了精度保持性試驗臺精度在線測試方法，提出了一種由滑塊相對基準距離變化換算成滑塊移動對基準面的平行度以及滑塊相對導軌的偏轉角度變化量的測控算法，解決了在線平行度和精度測量問題，為在線測量滾動直線導軌副精度保持性提供了一定指導。

參 考 文 獻

[ 1 ] 李薇. 一種滾動直線導軌副精度自動化檢測方法[J]. 組合機床與自動化加工技術，2010(3): 34-37.

LI Wei. One automatic measuring method of linear rolling guideway[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2010(3):34-37.

[ 2 ] 屠國俊，陶衛軍，馮虎田，等. 基于步進加載的重載滾動直線導軌副可靠性試驗方法[J]. 機床與液壓，2012,40(5): 4-7.

TU Guo-jun, TAO Wei-jun, FENG Hu-tian, et al. Reliability test method of overloaded linear rolling guide vice based on stepping loading[J].Machine Tool & Hydraulics,2012, 40(5):4-7.

[ 3 ] Tao Wei-jun, Zhong Yang, Feng Hu-tian,et al. Model for wear prediction of roller linear guides[J]. Wear,2013, (305): 260-266.

[ 4 ] JB/T7175.4-2006, 滾動直線導軌副第4部分: 驗收技術條件[S]. 北京：機械工業出版社，2006.

[ 5 ] 屠國俊. 滾動功能部件可靠性試驗、分析及評估方法研究[D]. 南京:南京理工大學, 2011．

[ 6 ] JB/0802201140000016, 滾動功能部件可靠性第5部分:滾動直線導軌副精度保持性試驗規范[S]. 2015.

[ 7 ] 陳宇，白征東，羅騰. 基于改進的布爾沙模型的坐標轉換方法[J]. 大地測量與地球動力學，2010, 30(3): 71-78.

CHEN Yu, BAI Zheng-dong, LUO Teng, An improved bursa model for coordinate transformation[J]. Journal of Geodesy and Geodynamics, 2010, 30(3): 71-78.

[ 8 ] 張萌，楊志勇，丁克良. 基于改進的布爾沙-沃爾夫模型的任意旋轉角坐標轉換方法的研究[J]. 北京測繪，2013(1): 16-35.

ZHANG Meng, YANG Zhi-yong, DING Ke-liang. Research on an improved bursa-wolf model for 3D coordinate transformation[J]. Beijing Surveying and Mapping,2013(1): 16-35.

[ 9 ] Tomas J. Prediction of wheel profile wear-comparisons with field measurements[J]. Wear, 2002, 253: 89-99.

[10] Ohta H, Hayashi E. Vibration of linear guideway type recirculating linear ball bearings[J]. Journal of Sound and Vibration, 2000,235: 847-861.

[11] 徐燁，李先鋒. 影響滾動直線導軌副運動精度因素的研究[J]. 機械，2000, 27: 60-61.

XU Ye, LI Xian-feng, Study on movement precision influencing factors of linear rolling guide[J]. Machinery, 2000, 27: 60-61.

Measurement method and tests for precision-keeping of a linear rolling guide based on online measuring

JIZhong-qing,OUYi,FENGHu-tian,ZHANGYun(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

Abstract:Aiming at the checking demands of precision-keeping for a linear rolling guide, a online measuring method for measuring its motion accuracy based on laser displacement sensor was presented. According to the relative motion theorem, using the proposed method, the diatance variations between slider and guide measured with 4 laster displacement sensors were converted into the variations of the guid’s level parallelism and the slider’s deflection angle. Then the online loss of precision of a linear rolling guide in actual running process was measured with the proposed method, and the feasibility of the online measuring principle was validated effectively through comparing the measured results with the linear rolling guide’s off-line data. Finally, error analysis was performed in many ways.

Key words:linear rolling guide; precision maintenance; experimental study; online testing

中圖分類號:TH132; P258

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2016.07.009

通信作者歐屹 男，博士，講師，1982年生

收稿日期：2015-02-28修改稿收到日期：2015-04-17

基金項目：國家重大科技專項(2012ZX04002021)

第一作者 姬中晴 女，碩士，1990年生