考慮橋面隨機不平順的橋梁動態響應研究

張建波， 廖敬波， 唐光武， 徐文濤

(1.重慶交通科研設計院 橋梁工程結構動力學國家重點實驗室，重慶　400067；2.鄭州大學 力學與工程科學學院，鄭州　450001)

?

考慮橋面隨機不平順的橋梁動態響應研究

張建波1,2， 廖敬波1， 唐光武1， 徐文濤2

(1.重慶交通科研設計院 橋梁工程結構動力學國家重點實驗室，重慶400067；2.鄭州大學 力學與工程科學學院，鄭州450001)

摘要：基于隨機振動理論研究橋面不平順影響下，車橋耦合振動作用時的中小橋梁動態響應曲線;通過建立車橋耦合振動方程，基于虛擬激勵法對重力引起的確定性激勵和橋面不平順引起的隨機激勵求解，得到橋梁跨中撓度和應力響應的均值和標準差。運用3σ法則定義隨機激勵的確定值值域，分析橋梁跨中位移和應力響應在不同車速和橋面不平順等級作用下的特性，并討論了動態響應曲線與準靜態影響線的差異。結果表明：橋梁跨中撓度和應力標準差受車速和橋面不平順等級變化的影響很大；橋梁動態響應值域范圍很大，具有較強的隨機性；相比準靜態影響線，動態響應曲線更能體現車橋之間激勵的耦合隨機作用。

關鍵詞：車橋耦合振動； 橋面不平順； 虛擬激勵法； 動態響應

隨著經濟的發展，交通運輸日益繁忙，橋梁作為道路交通的咽喉，其承載能力評定、結構安全性以及疲勞壽命的分析就顯得至關重要。作為研究橋梁承載能力和結構安全性的一種有效工具，影響線由于可以避開針對力學方程的反復求解而提高計算效率已經獲得許多專家的認可[1-3]。由于計算方法和工具的限制，傳統影響線的研究是基于結構準靜態移動載荷基礎上提出來的，并沒有考慮結構的動態效應。然而在橋梁實際運營中，由于橋面不平順的影響，行駛車輛與橋梁之間會產生較強的隨機振動。因此，在實際應用中，需要將移動載荷的準靜態影響線推廣到橋梁動態響應曲線范圍以滿足橋梁設計和結構分析的需求。

近年來，隨著橋梁結構損傷識別、橋梁承載能力評定以及橋梁移動載荷識別等研究方向的深入，相比準靜態影響線，橋梁動態響應時程曲線能真實反映行駛車輛作用下橋梁的實際狀態，因此更加受到人們的關注[4-5]。但有些文獻僅把移動載荷作為動態影響的主要原因[6]，而忽略了其中復雜的隨機作用；而有些文獻雖然考慮了橋面的隨機激勵，但大多將橋面不平順模擬為幾條樣本曲線的疊加，或采用有限的幾條樣本作為輸入，忽略了隨機問題的統計特性[7-8]。事實上，橋梁隨機響應與橋面不平順有密切的關系[9]，僅靠幾條樣本曲線，很難保證隨機問題本質的體現，但大量的樣本曲線又會使計算成本增加，計算效率降低。

虛擬激勵法是近年提出的一套簡潔、精確和高效的隨機響應計算方法，在地震工程、結構風振分析、列車-軌道-橋梁的隨機振動等多個方面取得了豐碩成果[10]，尤其在處理大規模隨機振動數值分析方面具有明顯優勢。但由于其基于譜分析的計算，輸出結果形式對于橋梁、土建等工程領域所需要的確定性結果尚需探討結合的方法。

本文將移動車輛與中小橋梁模型看作動態的隨機振動耦合體系，在充分考慮橋面隨機不平順的激勵作用情況下，研究了橋梁的動態響應曲線。基于虛擬激勵法對車輛與橋梁的非平穩隨機振動進行分析，并針對工程所需的內力、位移、撓度等確定性工程量值進行3σ法轉換，計算了橋梁跨中撓度和應力的動態響應，并研究了車速和橋面不平順等級對其的影響，分析了橋梁準靜態影響線與動態響應曲線的差異。

1車橋系統計算模型

將多軸移動車輛模型與中小橋梁模型的相互作用形式看作動態車橋耦合隨機振動系統，建立整體的動力學方程，其中隨機因素為橋面存在的高低不平順。

1.1多軸車輛-橋梁耦合隨機振動模型

以簡支梁和四自由度二分之一車輛模型為研究對象(見圖1)。其中：m0為車體質量；z0為車體的豎向位移；θ為車體繞橫向軸的轉角；Iz為車體轉動慣矩；m1、m2為車輛前后輪的質量；z1、z2為前后輪的豎向位移；Ks1、Ks2、Cs1和Cs2為前后懸掛裝置的彈簧剛度和阻尼系數；Kt1、Kt2、Ct1和Ct2為前后輪胎的剛度和阻尼系數；L1、L2為車輛前后軸到車體重心的距離。

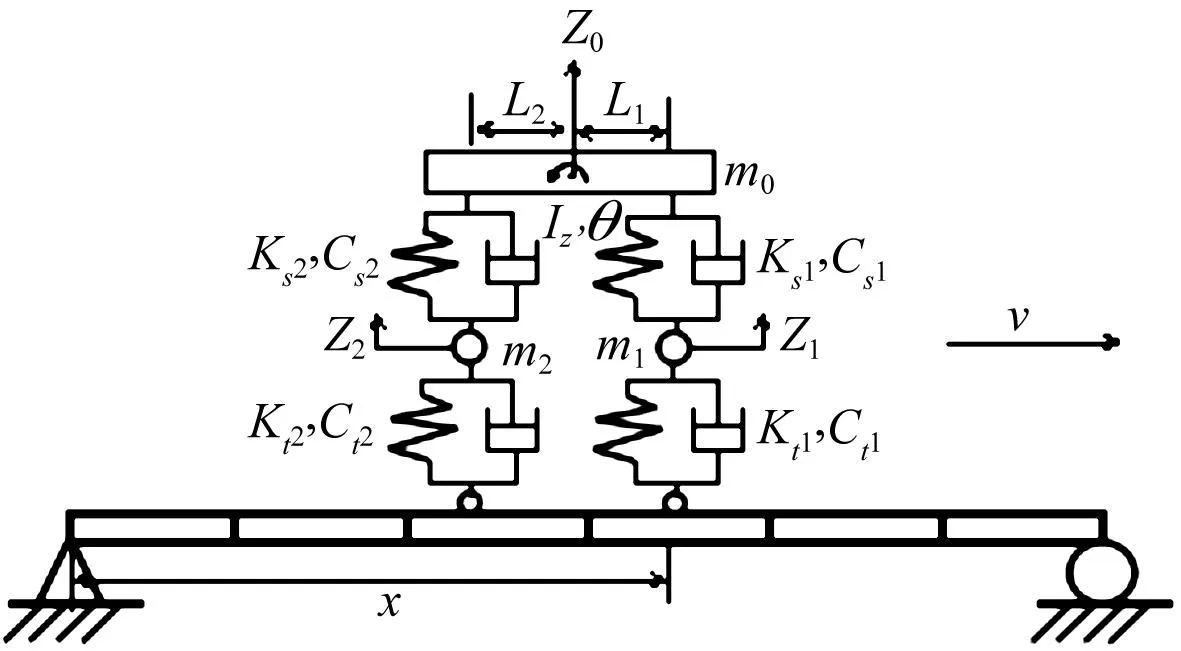
圖1　車輛與簡支梁橋模型Fig.1 The model of vehicle andsimply-supported beam

1.2車輛振動方程

車身假設為剛體，前后輪視為集中質量，并假設輪胎與橋面始終保持接觸狀態，利用達朗貝爾原理可以推導出車輛系統的振動方程

(1)

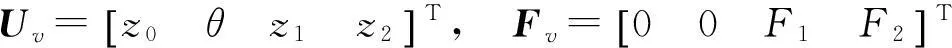
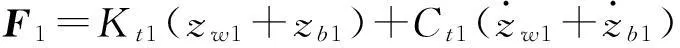
式中：Μv、Κv、Cv分別為車輛的質量、剛度和阻尼矩陣；F1、F2分別為橋梁對車輛前后輪的作用力；zb1、zb2為前后車輪與橋梁接觸點處的橋梁位移；zw1、zw2為接觸點處的橋面不平順位移。

由式(1)可知，車輛振動是由車輪與橋梁接觸點處的橋梁位移和橋面不平順共同作用引起的。

1.3橋梁振動方程

橋梁采用Bernoulli-Euler梁，通過有限元離散，可得其振動方程

(2)

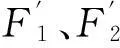
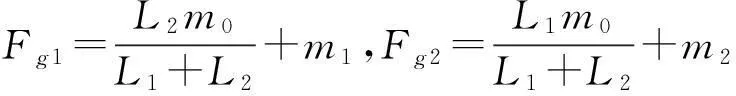
(3)

式中：N1、N2為前后車輪與橋梁接觸點處的單元形函數列向量。

1.4車橋耦合振動方程

通過車輪與橋梁接觸點處的位移協調條件和車橋相互作用力之間的平衡關系，可將車輛與橋梁兩個子系統的方程聯系起來，利用單元形函數N1、N2將車輛前后輪與橋梁接觸點處的作用力和位移轉換為節點載荷和節點位移，然后按有限元法的對號入座方法組裝車橋系統的質量、阻尼、剛度和載荷矩陣，則可得車橋耦合系統的時變方程

(4)

式中:

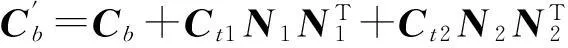
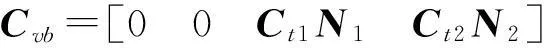
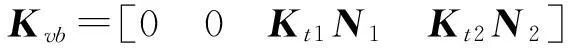
由式(4)可知，車橋時變系統的激勵項分為由車輛重力引起的確定性激勵Fg和由橋面不平順引起的隨機激勵Fw。

2車橋耦合系統的非平穩隨機響應

2.1橋面隨機激勵源

作為車橋耦合振動輸入的橋面不平順激勵，采用與路面相同的功率譜密度函數描述其統計特性。擬合表達式如下[11]：

(5)

式中：n為空間頻率(m-1)，它是波長λ的倒數，表示每米長度中包括幾個波長；n0為參考空間頻率，n0=0.1 m-1；Gqq(n0)為參考空間頻率n0下的路面功率譜密度函數值，稱為路面不平度系數；W為頻率指數，通常取W=2。根據我國公路實際情況，按路面功率譜密度把路面的不平程度分為8級，高等公路路面譜基本在A級、B級、C級三個級別范圍內，其中B級、C級占的比重較大。通過時域、頻域轉換，可以得到路面不平順激勵Gqq(n)與Gqq(f)的換算式：

(6)

將式(5)代入式(6)得到時間路面功率譜Gqq(f)×(m2s)的表達式

(7)

由圓頻率ω(rad/s)與時間頻率f的轉換關系ω=2πf可得圓頻率表達式

(8)

2.2隨機響應的均值

在橋面不平順作用下，車輛與橋梁之間會產生較強的非平穩隨機振動，利用虛擬激勵法可將其轉化為確定性的時間歷程進行分析，從而使計算量大大減少。橋面不平順假設為均勻調制演變隨機過程

w(x)=g(x)q(x)

(9)

(10)

g(x)為確定性慢變調制函數，q(x)為以空間坐標x為自變量的零均值平穩隨機過程，其功率譜密度函數Gqq(n)已知。

將橋面不平順由空間域轉換到時間域，即

w(t)=g(t)q(t)

(11)

式中：q(t)是以時間坐標t為自變量的零均值平穩隨機過程，其功率譜密度函數為Gqq(ω)。

車橋耦合系統方程的解可表示為[12]

(12)

式中：H(t-τ,τ)為脈沖響應矩陣。根據式(12)，系統響應的均值為

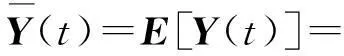
(13)

由于q(t)是零均值高斯過程，則式(13)可化為

(14)

由式(14)可知，車橋系統響應的均值是由確定性載荷Fg引起的。

2.3構造虛擬激勵

根據式(11),車輛前后輪與橋梁接觸點處的橋面不平順可表示為

zw1=g(t)q(t)，zw2=g(t-Δt)q(t-Δt)

(15)

Δt=(L1+L2)/v

(16)

式中:Δt為車輛前后輪通過橋面同一點的時間差。

對zw1、zw2求導可得其速度項

(17)

由于g(t)為慢變函數，故不對其求導。則車橋系統方程中的隨機激勵Fw1和Fw2可表示為

(18)

Fw2=Kt2g(t-Δt)q(t-Δt)+

(19)

則可將隨機激勵Fw改寫為

Fw=[Nk1Nk2]G(t)Q(t)+

(20)

式中:

Nk1=Kt1[0010N1]T；

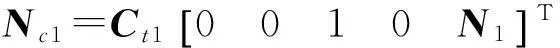
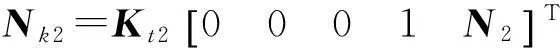
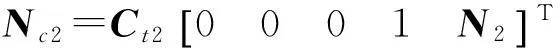
G(t)=diag[g(t),g(t-Δt)]；

根據隨機振動理論，橋面不平順及其一階導數的自功率譜和互功率譜關系如下

(21)

(22)

根據維納-辛欽關系可得

E[{Q(τ1)}{Q(τ2)}T]=

(23)

式中：V*是矩陣V的復共軛矩陣

V=diag[1,e-iωΔt]

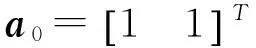
車橋系統響應的方差為

E[Fw(τ1)Fw(τ2)]HT(t-τ2,τ2)dτ1dτ2

(24)

聯立式(20)～式(23)并代入式(24)，系統響應的方差矩陣RYY(t)可化為

(25)

其中

G(t)Va0eiωtdτ

(26)

根據式(26)，構造如下虛擬激勵

(27)

則其引起的響應為

(28)

響應的功率譜矩陣為

(29)

3車橋時變系統方程求解

(30)

(31)

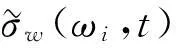
(32)

(33)

橋面不平順是平穩高斯過程，由概率理論知，高斯過程在線性運算下性質保持不變，所以橋梁的動態響應也是高斯型隨機變量，3σ準則是適用的，將橋梁跨中撓度和應力響應的均值加減三倍標準差可得其確定值值域。

4算例分析

車橋模型見圖1，簡支梁橋參數：橋長Lb=40 m，抗彎剛度EI=1.28×1011N·m2，單位長度質量m=1.20×104kg·m-1；車輛模型參數：m0=24 790 kg，L1=1.838 m，m1=m2=4 330 kg，L2=1.787 m，Ks1=Ks2=2.54×106N·m-1，Cs1=1.96×106N·s·m-1,Cs2=1.96×106N·s·m-1,Kt1=4.28×106N·m-1，Kt2=4.28×106N·m-1，Ct1=9.8×105N·s·m-1，Ct2=9.8×105N·s·m-1，Iz=3.258×106kg·m2。

分別考慮車輛行駛速度v為30 km/h、60 km/h、90 km/h、120 km/h和橋面不平順A級、B級、C級、D級四個等級，從A級到D級橋面不平順等級提高，路況逐漸變差，時間頻率范圍0.3～30 Hz，頻率增量為0.3 Hz。基于Matlab軟件對算例進行編程求解，獲得了不同車速下橋梁跨中撓度和應力響應的均值，并得到了橋面不平順等級為B級時不同車速下的橋梁跨中撓度和應力標準差時程曲線和車速為60 km/h時不同橋面不平順等級下的橋梁跨中撓度和應力標準差曲線。

4.1橋梁跨中撓度響應

由圖2～圖4可知，橋梁跨中撓度的標準差受車速和橋面不平順等級變化的影響很大，隨著橋面不平順等級的提高而成倍增加，但并不隨著車速的提高而單調遞增。車速變化對橋梁跨中撓度的均值影響不大，這是由于均值主要是由車輛前后軸重引起的。

由3σ法則知，橋梁跨中撓度的實際響應在均值加減三倍標準差的帶狀區域內。車速設置為60 km/h，橋面不平順等級為B級，計算可得橋梁跨中撓度動態響應的上下限，并與車速為1 km/h時的橋梁跨中準靜態響應進行對比(見圖5)。由圖5可知，橋梁跨中撓度的實際響應隨機性很強，并且隨著橋面不平順等級的提高，帶狀區域寬度會增大。相比較橋梁的動態響應，橋梁跨中撓度的準靜態影響線變化趨勢平緩，未能體現出車橋之間的相互作用。

圖6和圖7是不同車速和不同橋面不平順等級下橋梁撓度動態響應的最大值，圖6中橋面不平順等級為B級，圖7中車速為60 km/h。由圖6和圖7可知，橋梁撓度動態隨機響應受車速和橋面不平順等級變化的影響很大，相比較車速變化，橋面不平順等級變化的影響更加顯著。

圖2 不同車速下的橋梁跨中撓度均值Fig.2Meanvalueofdeflectioninthemidspanofbridgeunderdifferentvehiclevelocity圖3 不同車速下的橋梁跨中撓度標準差Fig.3Standarddeviationofdeflectioninthemidspanofbridgeunderdifferentvehiclevelocity圖4 不同橋面不平順等級下的橋梁跨中撓度標準差Fig.4Standarddeviationofdeflectioninthemidspanofbridgeunderdifferentstandardofbridgesurfaceroughness

圖5 橋梁跨中撓度的準靜態和動態響應Fig.5Quasi-staticresponseanddynamicresponseofdeflectioninthemidspanofbridge圖6 不同車速下的橋梁跨中撓度動態響應Fig.6Dynamicresponseofdeflectioninthemidspanofbridgeunderdifferentvehiclevelocity圖7 不同橋面不平順等級下的橋梁跨中撓度動態響應Fig.7Dynamicresponseofdeflectioninthemidspanofbridgeunderdifferentstandardofbridgesurfaceroughness

4.2橋梁跨中應力響應

由圖8～圖10可知，橋梁跨中應力的標準差受車速和橋面不平順等級變化的影響很大，其均值曲線受車速變化的影響不大。車輛行駛到橋梁中點前后時，橋梁跨中應力均值未有太大變化，這是由于車輛前后軸重相近。隨著橋面不平度等級的提高，橋梁跨中應力的標準差成倍增加。圖中標準差時程曲線呈現波浪狀，且隨著車速和橋面不平順等級的提高而愈加明顯，這是由橋面不平順作用下的隨機激勵引起的。

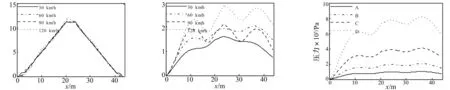
圖8 不同車速下的橋梁跨中應力均值Fig.8Meanvalueofstressinthemidspanofbridgeunderdifferentvehiclevelocity圖9 不同車速下的橋梁跨中應力標準差Fig.9Standarddeviationofstressinthemidspanofbridgeunderdifferentvehiclevelocity圖10 不同橋面不平順等級下的橋梁跨中應力標準差Fig.10Standarddeviationofstressinthemidspanofbridgeunderdifferentstandardofbridgesurfaceroughness

由圖11可知，橋梁跨中應力響應的隨機性比其撓度響應的隨機性更強，說明橋面不平順引起的隨機激勵對橋梁跨中應力的影響比對撓度的影響顯著。與撓度準靜態影響線相似，橋梁跨中應力準靜態影響線變化平緩，未能體現車橋之間的相互作用。

圖12工況設置與圖6一致，圖13工況設置與圖7一致。由圖12和圖13可知，橋梁應力隨機響應受車速和橋面不平順等級變化的影響很大。

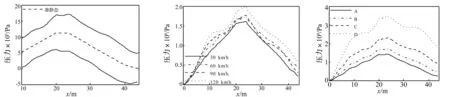
圖11 橋梁跨中應力的準靜態和動態響應Fig.11Quasi-staticresponseanddynamicresponseofstressinthemidspanofbridge圖12 不同車速下的橋梁跨中應力動態響應Fig.12Dynamicresponseofstressinthemidspanofbridgeunderdifferentvehiclevelocity圖13 不同橋面不平順等級下的橋梁跨中應力動態響應Fig.13Dynamicresponseofstressinthemidspanofbridgeunderdifferentstandardofbridgesurfaceroughness

5結論

本文采用虛擬激勵法和Newmark-β積分法對橋面不平順作用下車輛與橋梁的隨機振動方程進行求解，系統的分析了車速變化和橋面不平順等級變化對橋梁跨中撓度和應力的影響，并對隨機振動作用下準靜態影響線與動態響應時程曲線的差異進行了分析，結論如下：

(1) 對橋梁影響線的關注應考慮車輛-橋梁系統的動態效應及隨機振動因素。

(2) 橋梁動態響應的標準差對車輛速度變化具有較強的敏感性，這些區別在以準靜態方法為主的研究中不易被體現，而在動力學分析中能夠得到充分考慮。

(3) 橋梁表面高低不平順的隨機特性對橋梁的動態響應具有顯著的影響，并且有較大的貢獻。相比僅考慮車輛移動效應的研究，其響應增大了20%多，說明橋梁影響線的研究不應忽略橋面不平順造成的效應。

(4) 橋梁動態響應由于隨機作用的存在，其結果應是一個值域，準靜態影響線只是其中的一條曲線。

參 考 文 獻

[ 1 ] 喬雅敏，丁建婷. 影響線計算的簡化及其在連續梁計算中的應用[J].東北公路，1999, 22(3): 40-42.

QIAO Ya-min, DING Jian-ting. Simple calculation of influence line and its application in design of continuous beam[J].Northeastern Highway, 1999, 22(3): 40-42.

[ 2 ] 廖敬波，唐光武，張又進，等. 實測準靜態廣義影響線在橋梁結構靜載試驗中的應用研究[J].公路交通技術，2009, 12(6): 65-68.

LIAO Jing-bo, TANG Guang-wu, ZHANG You-jin,et al. Research on application of measured quasistatic generalized influence line in static load test for bridge structure[J].Technology of Highway and Transport, 2009, 12(6): 65-68.

[ 3 ] 譚東蓮. 基于影響線理論應用檢測信息反演橋上車輛載荷[J].力學與實踐，2008, 30(2)：62-66.

TAN Dong-lian. Inversion of vehicle load on bridge from the monitoring information based on the theory of influential line[J].Mechanics in Engineering, 2008, 30(2)：62-66.

[ 4 ] He X L, Yang X S, Zhao L Z. New method for high-speed railway bridge dynamic deflection measurement[J].Journal of Bridge Engineering, 2014, 19(7): 612-623.

[ 5 ] Lacarbonara W, Colone V. Dynamic response of arch bridges traversed by high-speed trains[J].Journal of Sound and Vibration, 2007, 304(1/2): 72-90.

[ 6 ] Xu Y L, Li Q, Wu D J, et al. Stress and acceleration analysis of coupled vehicle and long-span bridge systems using the mode superposition method[J].Engineering Structures, 2010, 32(5): 1356-1368.

[ 7 ] Majka M, Hartnett M. Dynamic response of bridges to moving trains: A study on effects of random track irregularities and bridge skewness[J].Computers and Structures, 2009, 87(19/20): 1233-1252.

[ 8 ] 王寧波，任偉新，李苗. 基于影響線的移動載荷識別[J].振動與沖擊，2013, 32(3): 129-133.

WANG Ning-bo , REN Wei-xin, LI Miao. Moving load identification of abridge based on influence line[J].Journal of Vibration and Shock, 2013, 32(3): 129-133.

[ 9 ] 葉茂，張鵬，傅繼陽，等. 帶彈性支撐多跨連續梁橋的車橋耦合演變隨機振動[J]. 振動與沖擊，2014，33(3):76-82.

YE Mao, ZHANG Peng, FU Ji-yang, et al. Coupled vehicle-bridge evolutionary random vibration for a multi-span continuous bridge with elastic bearings[J]. Journal of Vibration and Shock, 2014, 33(3):76-82.

[10] 林家浩，張亞輝. 隨機振動的虛擬激勵法 [M].北京：科學出版社，2004.

[11] 余志生. 汽車理論 [M].5版. 北京：機械工業出版社，2009.

[12] 張志超. 車橋系統耦合振動和地震響應的隨機分析 [D]. 大連：大連理工大學，2010.

Dynamic response of a bridge considering its surface random roughness

ZHANGJian-bo1,2,LIAOJing-bo1,TANGGuang-wu1,XUWen-tao2(1. State Key Laboratory of Bridge Engineering Structural Dynamics,Chongqing Communications Research & Design Institute, Chongqing 400067, China;2. School of Mechanics & Engineering Science, Zhengzhou University, Zhengzhou 450001, China)

Abstract:Based on the random vibration theories, dynamic response curves of short and medium-span girder bridges considering vehicle-bridge coupling and bridge surface rough ness were studied. The dynamic equations of the vehicle-bridge coupled system were solved using the pseudo-excitation method (PEM), and the mean values and standard deviations of the deflection and stress of the bridge’s were calculated. Based on the 3σ method, the statistical solutions were converted into deterministic value ranges, attracted by attention of engineering researchers. The results showed that the standard deviations of the deflection and stress at the mid span of the bridge are greatly affected by vehicle velocity and bridge surface roughness level; the value range for the bridge’s dynamic response is large and more strongly random; compared with the quasi-static influence line, the dynamic response curves reflect the interaction of vehicle-bridge more evidently.

Key words:vehicle-bridge coupling vibration; bridge surface roughness; pseudo-excitation method; dynamic response

中圖分類號:U441.3

文獻標志碼：A

DOI:10.13465/j.cnki.jvs.2016.07.033

通信作者徐文濤 男，博士，副教授，1980年生

收稿日期：2014-12-18修改稿收到日期：2015-04-14

基金項目：橋梁工程結構動力學國家重點實驗室開放基金資助(201403)

第一作者 張建波 男，碩士，1992年生