單OSV服務多衛星的轉移軌道優化研究

劉慶國, 劉新學

(火箭軍工程大學 906教研室, 陜西 西安 710025)

?

單OSV服務多衛星的轉移軌道優化研究

劉慶國, 劉新學

(火箭軍工程大學 906教研室, 陜西 西安 710025)

摘要:利用混合法解決了有限推力作用下單OSV服務多衛星的轉移軌道優化問題。首先從OSV攜帶燃料的角度出發,初步篩選出在其服務范圍內的服務對象,基于雙脈沖交會假設,確定了服務序列以及時間節點;其次針對每一段轉移軌道,利用Pontryagin極小值原理推導出最優控制律,設定開-關-開的發動機工作方式,將初始協態變量和開關機時間進行參數化處理,采用遺傳算法對非線性規劃問題進行求解;最后對整條軌道進行拼接優化。仿真結果表明,混合法對協態變量初值猜測敏感性小,降低了搜索最優轉移軌道的難度,且控制軌線光滑。

關鍵詞:服務序列; 有限推力; 混合法; 軌道優化

0引言

航天器在軌服務是指在空間通過人、機器人或兩者協同完成涉及延長各種航天器壽命、提升執行任務能力的一類空間操作[1]。在軌服務航天器(On-Orbit Service Vehicle,OSV)主要任務包括在軌裝配、在軌維護和后勤支持[2]。相對 “單對單”的服務方式來說,單個OSV服務多衛星的“單對多”服務方式能夠有效降低費效比,同時省去地面準備、發射入軌的時間,響應速度更快。文獻[3]對單個OSV的服務范圍進行了定量分析,其推力模型為單脈沖。文獻[4-5]分別就OSV“單對多”和“多對多”的任務分配問題進行了研究,但其軌道優化模型均為脈沖條件下“單對單”的問題。現有關于OSV在軌服務的軌道優化模型大多為“單對單”的服務方式,推力模型為脈沖推力,而對于有限推力作用下OSV“單對多”轉移軌道優化的研究相對較少。

由于直接解決有限推力作用下“單對多”的轉移軌道問題優化變量較多,所以本文分兩步求解此問題。首先確定服務序列,從OSV攜帶能量的角度出發,初步篩選出服務對象,根據雙脈沖交會假設進行全局優化搜索,確定了服務序列以及時間節點,為有限推力作用下的轉移軌道優化提供初值;其次進行轉移軌道優化,基于混合法建立了有限推力作用下的軌道優化模型,對整條軌道進行拼接優化;最后對提出的單OSV服務多衛星的轉移軌道優化模型進行了仿真計算。

1確定服務序列

有限推力作用下直接對轉移軌道進行優化的計算十分復雜。為簡化計算,首先對服務對象進行篩選,縮小可行解的范圍;然后基于雙脈沖交會假設,以速度增量作為性能指標,進行全局優化搜索,確定脈沖作用下的服務序列以及時間節點,為有限推力作用下轉移軌道的優化提供初值。

1.1篩選服務對象

OSV對于服務對象的篩選主要是從兩方面考慮:一是服務對象的任務優先級別,在OSV進行服務之前,應選擇任務優先級別較高的部分衛星作為預選服務對象;二是考慮OSV的服務范圍,由于OSV攜帶的燃料是有限的,單個OSV很難實現對所有目標的在軌服務,所以要確定OSV的服務范圍,對于服務范圍之外的預選服務對象應予排除。

本文對OSV服務范圍的確定是一個比較簡略的全局優化,其目的在于排除不可行解,縮小可行解的范圍,減少后續在確定服務序列的計算量。在忽略各種攝動力的前提下,從軌道能量的角度出發,確定OSV的服務范圍,即能夠實現軌道交會的范圍。OSV的機械能[6]為:

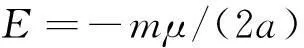
(1)

式中:m為OSV的質量;μ為引力常數;a為軌道半長軸。假設OSV的燃料所能轉化的機械能用Efu表示,其自身機械能用E1,燃料的質量為mfu,則OSV能進行服務的衛星軌道半長軸應滿足以下關系:

(2)

通過以上兩步,即可初步篩選出服務對象。

1.2基于遺傳算法的服務序列確定

(3)

其約束條件為:

(4)

式中:i=1,2,…,n;t1,t3,…,t2n-1為轉移時刻;t2,t4,…,t2n為交會時刻;Tmax為OSV與服務對象運行周期的最小公倍數;tserve為OSV與服務對象交會后的服務時間;Fmax為OSV推力最大值;g0為重力加速度;Isp為發動機比沖;ω為衡量脈沖轉換為有限推力的難度系數;n為子段數目;ΔVi為第i段軌道的速度增量;ΔVmax為最大速度增量;Δmi為第i段轉移軌道所消耗的燃料質量,計算如下:

(5)

式中:mi為第i段軌道的起始時刻質量。

利用遺傳算法對轉移時刻和交會時刻進行全局優化搜索,進而通過求解二體Lambert問題[7]得到雙脈沖交會的速度增量。圖1給出了雙脈沖交會示意圖。

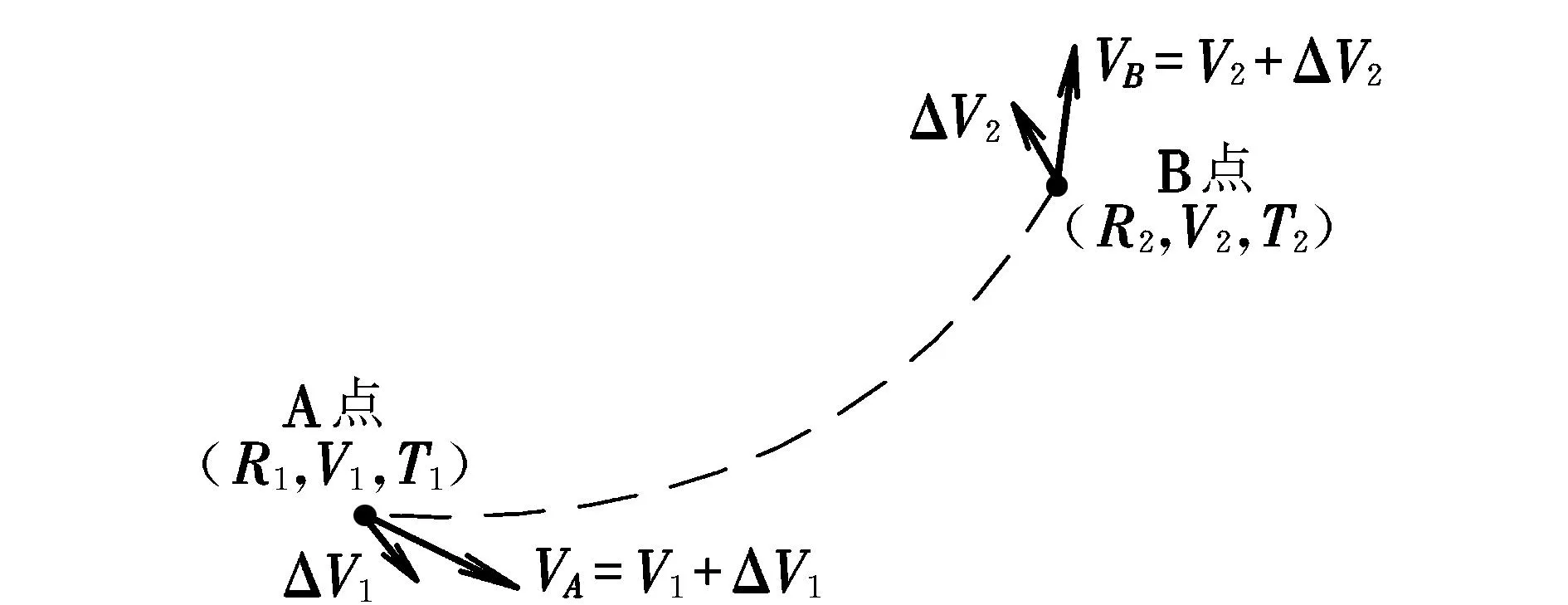
圖1　雙脈沖交會示意圖Fig.1　Schematic diagram of double-pulse rendezvous hypothesis

遺傳算法的實現步驟如下:

(1)對轉移時刻和交會時刻t0,t1,t2,…,t2n-2進行編碼,隨機產生50個染色體作為初始種群,設置交叉概率為Pc,變異概率為Pm,最大迭代次數為N。

(2)給出適應度函數:

計算種群個體的適應度值及群體的適應度值總和。

(3)利用RWS方法進行選擇,然后進行交叉、變異,生成新一代種群。

(4)重復執行(2)和 (3),直到算法收斂或者達到最大迭代次數。

2轉移軌道優化

轉移軌道的優化包括兩方面:一是每一段軌道的優化,由1.2節得到的結果可以將每一段軌道轉化為兩端狀態固定的最優控制問題,進而采用混合法對轉移軌道進行優化;二是整條軌道的優化,本文采用拼接優化的方法進行處理。

2.1動力學模型

本文使用地心赤道慣性坐標系下的二體模型:

(6)

式中:r,v分別為位置矢量和速度矢量;F為發動機推力;α=[αx,αy,αz]T為推力方向的單位矢量。

2.2基于混合法的轉移軌道優化模型

以燃料最優作為其性能指標:

(7)

式中:t0,tf分別為每一段軌道的起始時刻和終端時刻。

根據Pontryagin極小值原理[8],引入Hamiltonian函數:

(8)

式中:λr,λv為狀態量的協態變量;λm為質量m的協態變量。

最優推力方向矢量α*應使Hamiltonian函數最小,利用?H/?α=0以及約束‖α‖=1,從而得到最優推力方向為:

(9)

對協態變量求偏導數,得到協態變量滿足的微分方程如下:

(10)

OSV的初始邊界條件為:

(11)

終端邊界約束為:

(12)

對于有限推力作用下的最優控制為開關形式(bang-bang控制)的發動機策略。Hamiltonian函數對推力F求偏導可得開關函數S(t),以及推力狀態F(t):

(13)

(14)

本文采用的發動機開關策略為開-關-開發動機工作序列,并猜測相應的開關機時間。在得到上述方程以后,混合法將軌道優化問題轉化為針對參數β的優化問題,β將包括協態變量初值,以及開機時刻ton和關機時刻toff:

(15)

式中:λ1(t01),λ2(t02)分別為每一段軌道中兩個推力段的初始協態變量。

非線性規劃問題具體表述如下:

目標函數為:

(16)

約束條件由式(6)、式(9)～式(12)構成,待優化變量為式(15)。

此非線性規劃問題的待優化變量有16個,計算維度高,運算量大,難以用一般的啟發式算法解決。遺傳算法對于初值不敏感,全局搜索能力強,適合解決此類問題。在利用遺傳算法時,將參數β將作為其設計向量進行編碼,其適應度函數為:

(17)

其具體的算法流程上文已經提到,這里不再贅述。

2.3 拼接優化

以上是針對每一段轉移軌道的優化,對于整條軌道來說,可以采用拼接的方式將轉移軌道連接起來,進而得到全局最優解:

(18)

3仿真計算及分析

3.1仿真條件

本文給定OSV以及9顆衛星(S1～S9)的軌道參數如表1所示。以表1中的數據作為0時刻軌道參數,要求在8 h內完成對其中三顆衛星的在軌維修服務,對每顆衛星的在軌服務時間不小于0.5 h。

其余參數如下:Isp=2 000 s,Fmax=400 N,OSV的質量為1 000 kg,攜帶燃料100 kg,脈沖最大值Δvmax=0.8 km/s,發動機熱能轉換為機械能的效率為0.8,每千克燃料產生的熱能為7.5×106J,脈沖轉換為有限推力的難度系數ω=0.8,重力加速度g0=9.8 m/s2。

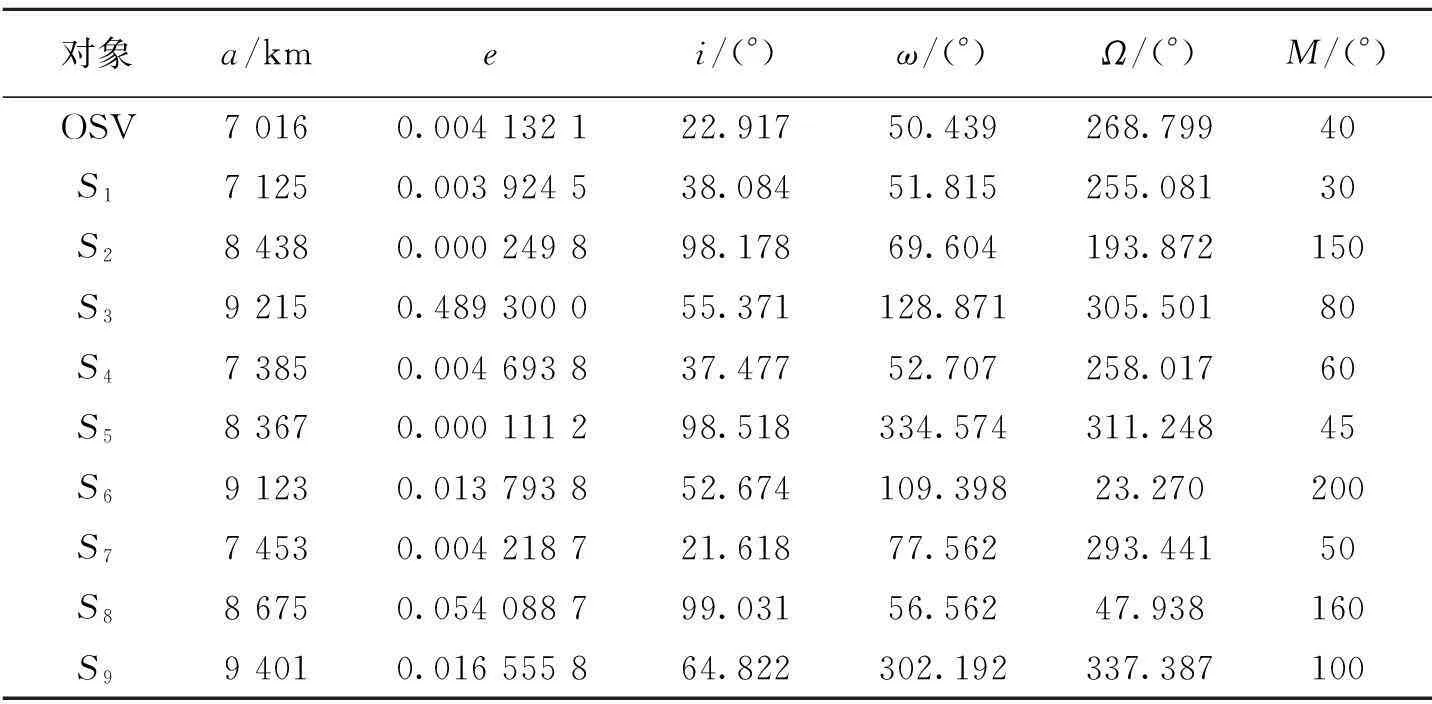
表1　衛星軌道參數

3.2仿真結果及分析

根據式(2)可以求出OSV能夠進行服務的最大軌道半長軸為8 894.943 km,得到預選服務對象為(S1,S2,S4,S5,S7,S8)。采用遺傳算法求解基于雙脈沖交會假設的最優服務序列及時間節點如表2所示,總速度增量為2.461 km/s。從表2中可以看出,OSV以雙脈沖交會進行軌道轉移,耗時7.17 h完成了對S1,S4和S7的在軌服務,滿足任務中的時間要求。

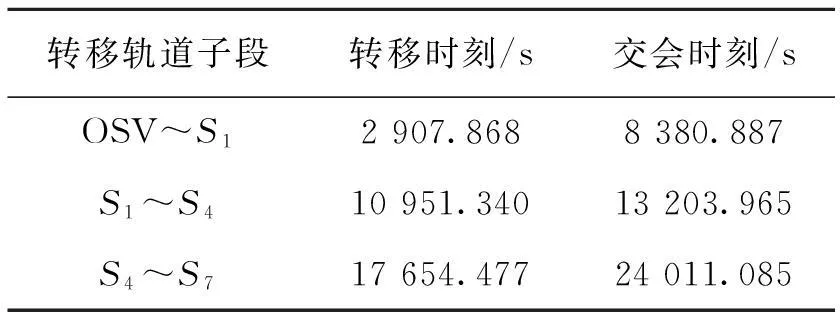
表2　服務序列及時間節點

在此基礎上求解有限推力作用下的推力大小和方向隨時間的變化,如圖2～圖8所示。

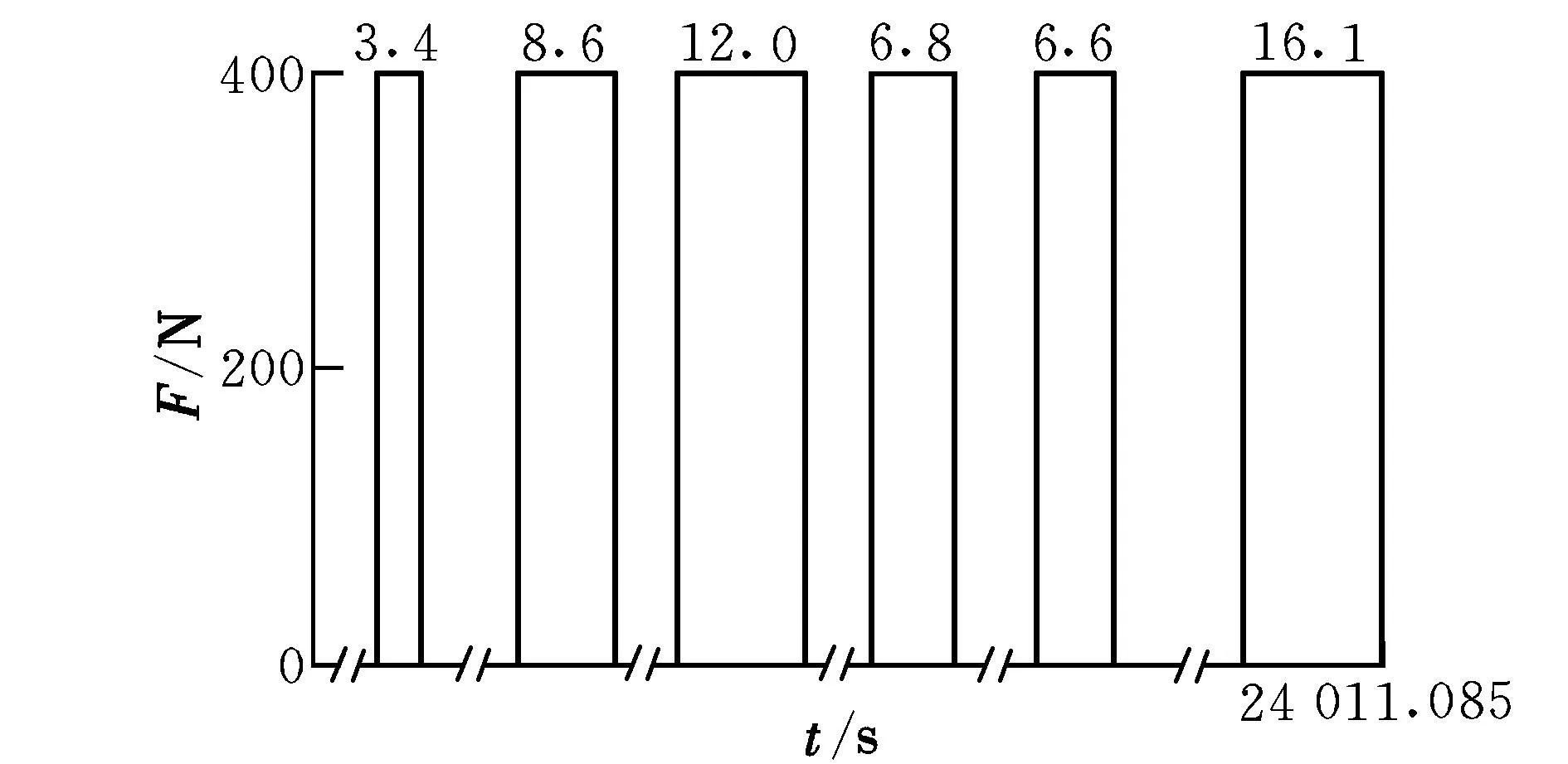
圖2　推力變化曲線Fig.2　Curve of thrust variation

從圖2中可以看出:OSV的發動機工作6段,每段工作時間分別為3.4 s,8.6 s,12 s,6.8 s,6.6 s,16.1 s,總工作時間為53.5 s;消耗燃料只占OSV攜帶燃料的1.09%,OSV能夠節省更多的燃料進行軌道保持或者對服務衛星實施燃料補充。

圖3～圖8為OSV發動機進行工作的6段時間內最優推力方向矢量的變化曲線。

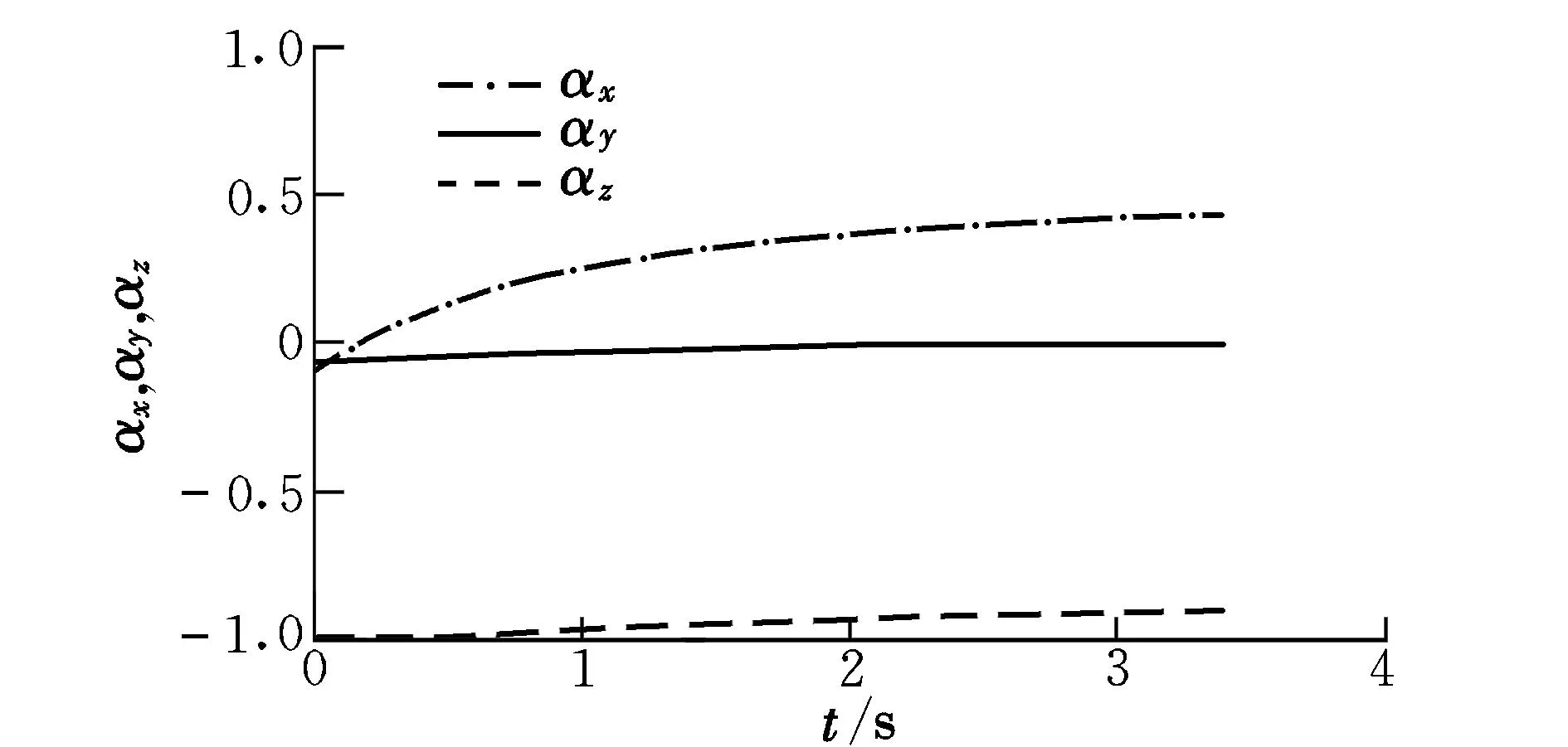
圖3　第1段最優推力方向矢量Fig.3　The 1st vector of optimal thrust direction

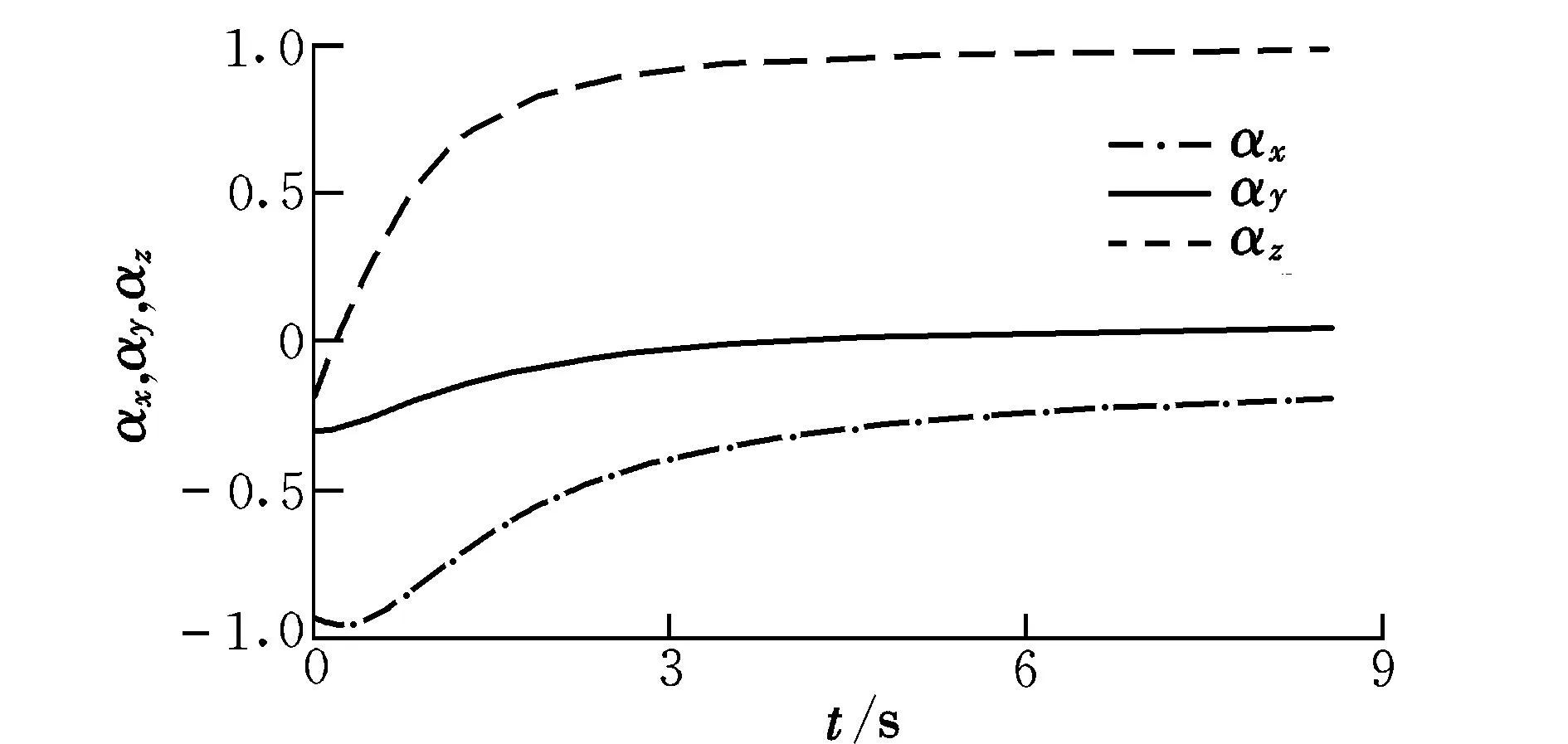
圖4　第2段最優推力方向矢量Fig.4　The 2nd vector of optimal thrust direction

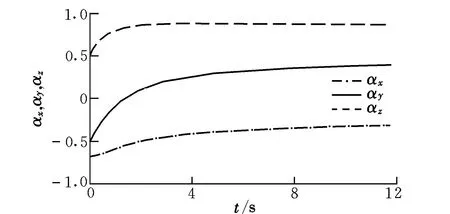
圖5　第3段最優推力方向矢量Fig.5　The 3rd vector of optimal thrust direction

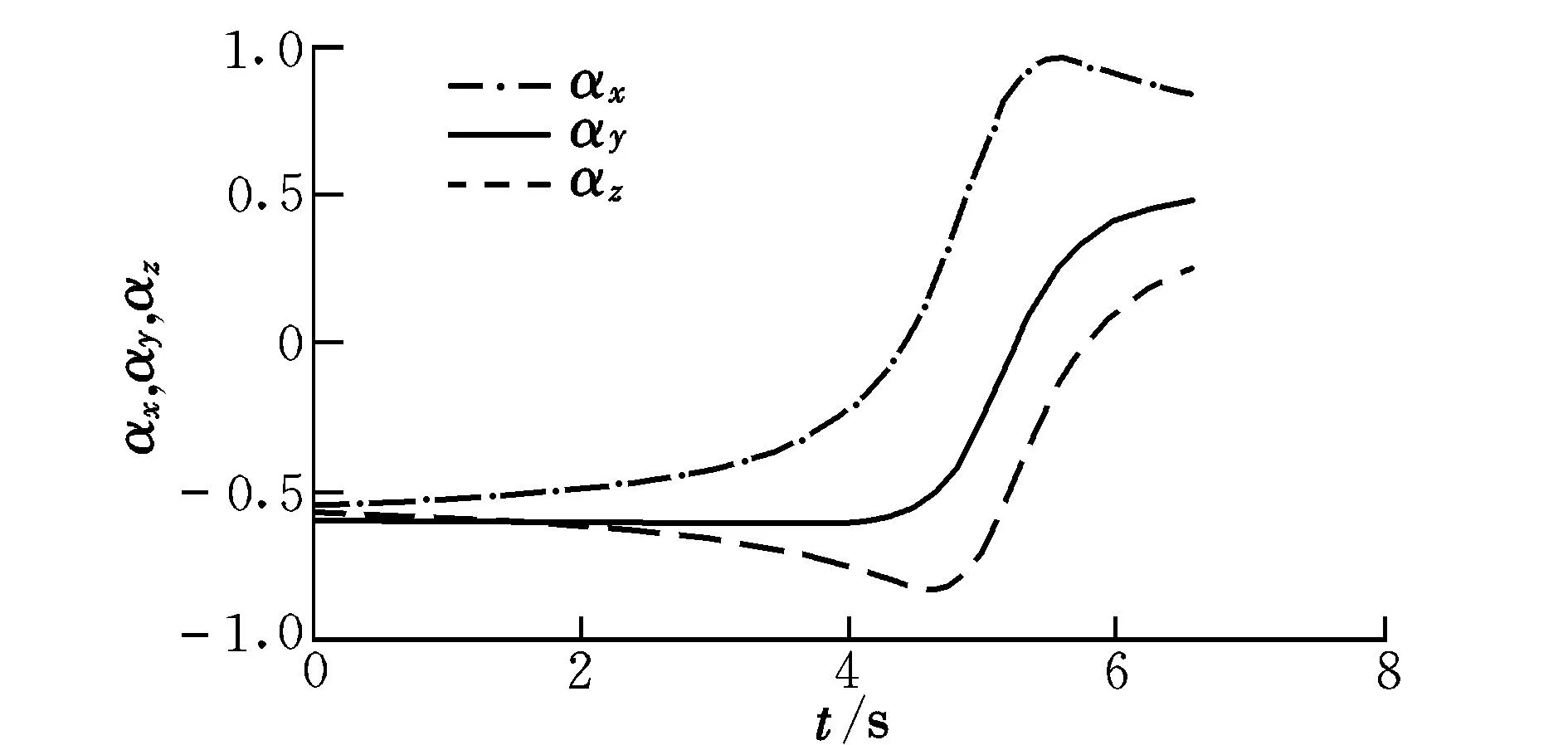
圖6　第4段最優推力方向矢量Fig.6　The 4th vector of optimal thrust direction

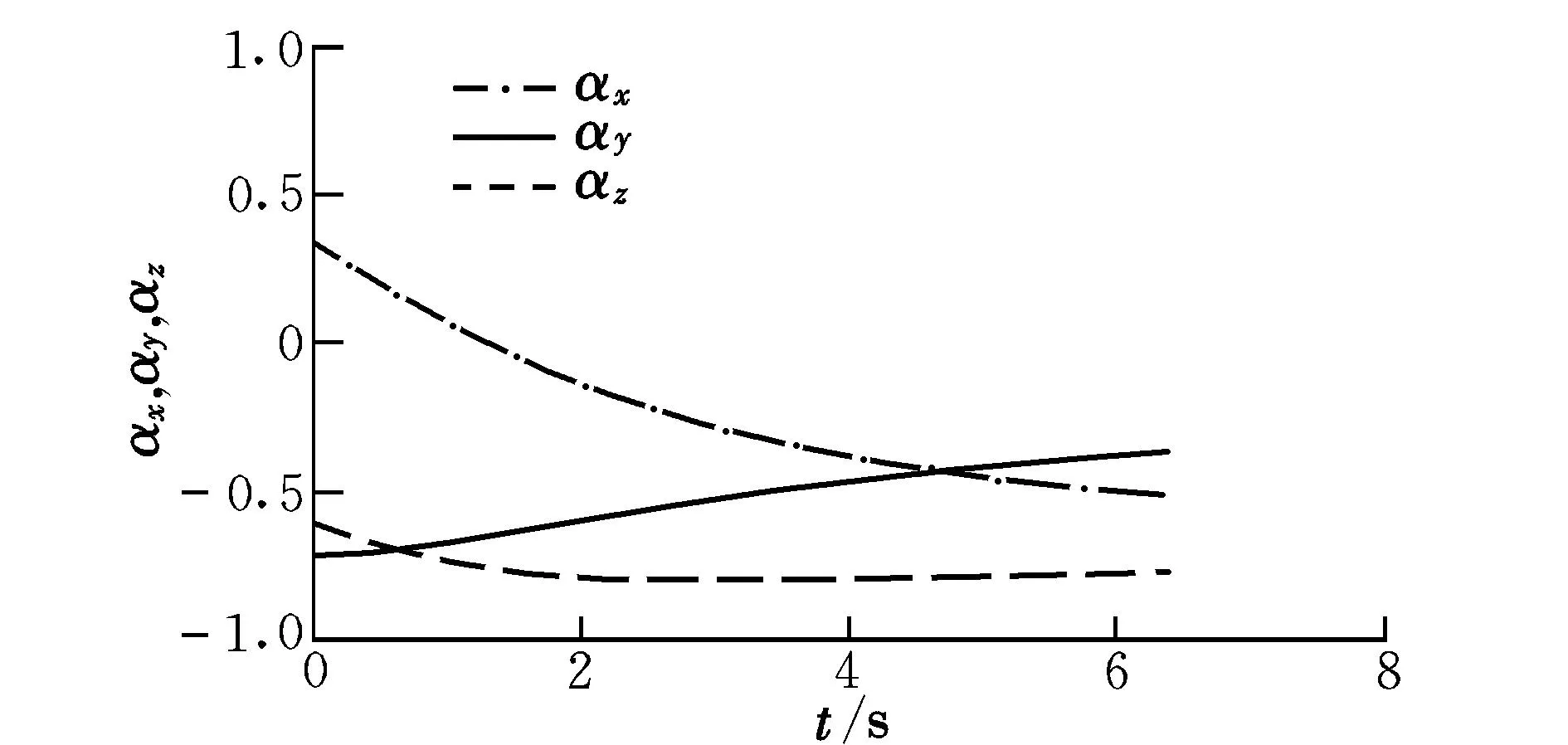
圖7　第5段最優推力方向矢量Fig.7　The 5th vector of optimal thrust direction

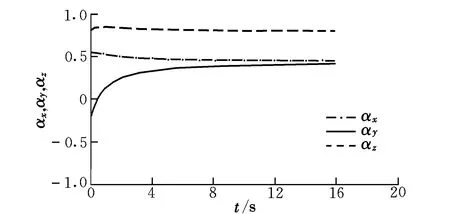
圖8　第6段最優推力方向矢量Fig.8　The 6th vector of optimal thrust direction

圖9為OSV從第一次轉移時刻2 907.868 s到轉移結束時刻24 011.085 s的三維軌跡。

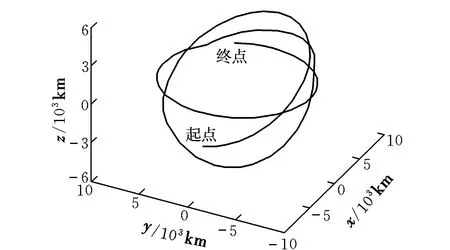
圖9　OSV的轉移軌道Fig.9　The transfer orbit of OSV

從上述結果可以看出,本文提出的方法對優化OSV服務多衛星的轉移軌道是有效的,得到的控制軌線也比較光滑。

4結束語

本文首先確定服務順序以及相應的時間節點,然后利用轉移軌道的共軛狀態來描述控制變量,設定開-關-開的發動機工作方式,舍棄了間接法中的橫截條件,擴大了優化問題的收斂半徑,解決了有限推力作用下單OSV服務多衛星的轉移軌道優化問題,進一步豐富了OSV轉移軌道優化的理論。本文采用遺傳算法求解高維的非線性規劃問題,由于具備大范圍搜索特性的優化算法很多,所以在選取計算精度更高、收斂速度更快的優化算法方面仍然值得進一步研究。

參考文獻：

[1]Waltz D.On-orbit servicing of space systems[M].Florida:Krieger Publishing Company,1993:6.

[2]陳小前,袁建平,姚雯,等.航天器在軌服務技術[M].北京:中國宇航出版社,2009:3.

[3]李巖,蔡遠文,同江.在軌服務飛行器服務范圍的定量分析[J].哈爾濱工程大學學報,2011,32(6):773-779.

[4]梁彥剛,王偉林.在軌服務飛行器任務指派問題[J].國防科技大學學報,2013,35(5):26-29.

[5]張琪新,孫富春,許斌,等.基于離散粒子群算法的多飛行器在軌服務任務分配[J].中國空間科學技術,2012 (2):68-75.

[6]俞輝,李俊峰,寶音賀西.多顆小行星探測序列確定及軌跡優化[J].清華大學學報(自然科學版),2007,47(11):2052-2055.

[7]趙瑞安.空間武器軌道設計[M].北京:中國宇航出版社,2008:155-181.

[8]程國采.航天飛行器最優控制理論與方法[M].北京:國防工業出版社,1999:55-58.

(編輯：崔立峰)

Optimization research on transfer trajectory of single OSV serving multi satellites

LIU Qing-guo, LIU Xin-xue

(Faculty 906, Rocket Force Engineering University, Xi’an 710025, China)

Abstract:This paper presents the method of optimizing the finite-thrust transfer trajectory of OSV serving multi satellites with the hybrid method. Firstly, the objects served were preliminarily selected within the service range according to the fuel taken by OSV, and based on the double pulse rendezvous hypothesis, the service sequence and time nodes were determined. Secondly, for each segment of the whole transfer trajectory, the optimal control law was derived by Pontryagin’s minimum principle, the engine operating mode was set to be on-off-on, the initial values of adjoint variables and the switching time were parameterized, and nonlinear programming was solved by genetic algorithm. Finally, the whole trajectory was optimized by mosaic method. The results of simulation show that the initial values guess sensitivity of adjoint variables is low by hybrid method, which reduces the difficulty of searching optimal transfer trajectory, and the control steering is smooth.

Key words:service sequence; finite thrust; hybrid method; trajectory optimization

中圖分類號：V412.4

文獻標識碼：A

文章編號：1002-0853(2016)02-0059-05

作者簡介:劉慶國(1991-)，男，山東泗水人，碩士研究生，研究方向為導彈彈道與火力運用。

收稿日期:2015-05-26;

修訂日期:2015-08-31; 網絡出版時間:2015-09-23 16:25