高空長航時(shí)飛翼布局無人機(jī)靜氣動(dòng)彈性研究

張強(qiáng), 祝小平, 周洲, 王偉

(1.西北工業(yè)大學(xué) 航空學(xué)院, 陜西 西安 710072;2.西北工業(yè)大學(xué) 第365研究所, 陜西 西安 710065)

?

高空長航時(shí)飛翼布局無人機(jī)靜氣動(dòng)彈性研究

張強(qiáng)1, 祝小平2, 周洲1, 王偉1

(1.西北工業(yè)大學(xué) 航空學(xué)院, 陜西 西安 710072;2.西北工業(yè)大學(xué) 第365研究所, 陜西 西安 710065)

摘要:高空長航時(shí)大展弦比飛翼布局無人機(jī)在氣動(dòng)載荷的作用下所產(chǎn)生的較大的彈性變形,顯著地改變了全機(jī)的升阻特性及靜穩(wěn)定性,常規(guī)的剛性飛機(jī)假設(shè)已不能滿足其總體氣動(dòng)特性分析的精度要求。基于CFD/CSD松耦合的方法研究了大展弦比飛翼布局無人機(jī)的靜氣動(dòng)彈性特性問題,結(jié)果表明:靜氣動(dòng)彈性效應(yīng)將顯著降低這類飛機(jī)的升阻特性,并顯著增加原設(shè)計(jì)配平巡航點(diǎn)的俯仰力矩;滾轉(zhuǎn)靜穩(wěn)定性導(dǎo)數(shù)可提高41.7%,同時(shí)改善了剛體外形設(shè)計(jì)中存在的縱向靜不穩(wěn)定現(xiàn)象;局部氣動(dòng)載荷顯著地向翼根轉(zhuǎn)移,從而有利于結(jié)構(gòu)設(shè)計(jì)。

關(guān)鍵詞:飛翼無人機(jī); 靜氣動(dòng)彈性; CFD/CSD耦合; 升阻比; 靜穩(wěn)定性

0引言

與常規(guī)布局飛機(jī)相比,飛翼布局無人機(jī)具有較高的升阻比、較輕的空機(jī)重量,以及優(yōu)良的隱身特性等,在無人戰(zhàn)斗、無人偵察、監(jiān)測、預(yù)警等領(lǐng)域具有廣闊的應(yīng)用前景[1]。高空長航時(shí)飛翼布局無人機(jī)往往具有大展弦比、輕質(zhì)等結(jié)構(gòu)特點(diǎn),在氣動(dòng)載荷的作用下,其機(jī)翼會(huì)產(chǎn)生較大的彎曲和扭轉(zhuǎn)變形。這種彈性變形會(huì)引起機(jī)翼氣動(dòng)載荷的重新分布,從而對(duì)全機(jī)的氣動(dòng)特性,如升阻特性、縱向和橫航向穩(wěn)定性等產(chǎn)生較大影響[2]。高空長航時(shí)飛翼布局無人機(jī)對(duì)升阻比的變化較為敏感;同時(shí),由于飛翼布局飛機(jī)沒有垂尾,其航向穩(wěn)定性也難以保證。基于此,研究氣動(dòng)彈性變形對(duì)大展弦比飛翼布局無人機(jī)的氣動(dòng)特性和飛行穩(wěn)定性的影響具有重要意義。

目前,關(guān)于飛機(jī)氣動(dòng)彈性研究主要有風(fēng)洞試驗(yàn)和數(shù)值模擬等方法。風(fēng)洞試驗(yàn)由于難以測得準(zhǔn)確的試驗(yàn)數(shù)據(jù),且成本高,因此,數(shù)值模擬在氣動(dòng)彈性研究中得到了廣泛的應(yīng)用[3]。經(jīng)典的靜氣動(dòng)彈性分析方法主要采用升力面理論,如MSC.flightload模塊,難以預(yù)測跨聲速區(qū)出現(xiàn)的激波、流動(dòng)分離等非線性現(xiàn)象。隨著計(jì)算流體力學(xué)(CFD)和計(jì)算結(jié)構(gòu)力學(xué)(CSD)以及計(jì)算機(jī)硬件技術(shù)的發(fā)展,耦合CFD(基于歐拉方程或N-S方程)和CSD進(jìn)行非線性氣動(dòng)彈性問題的精確計(jì)算逐漸變得可行,并得到了快速發(fā)展[4]。CFD和CSD耦合方式一般分為全耦合、緊耦合和松耦合等。全耦合[5]將氣動(dòng)和結(jié)構(gòu)方程整合為一個(gè)大的方程組,這些方程在時(shí)間步長內(nèi)要求同時(shí)求解,由于流固兩場物理特性的差異,用單一的數(shù)值求解方法存在很大困難;而對(duì)于松耦合[6],氣動(dòng)和結(jié)構(gòu)在各自的物理域內(nèi)獨(dú)立求解,可以充分利用現(xiàn)存的氣動(dòng)和結(jié)構(gòu)求解模塊,只需在適當(dāng)?shù)臅r(shí)間點(diǎn)進(jìn)行氣動(dòng)/結(jié)構(gòu)界面的數(shù)據(jù)交換,并反復(fù)迭代,直至求解收斂。

在本文中,氣動(dòng)載荷計(jì)算采用三維雷諾平均N-S方程作為控制方程,結(jié)構(gòu)變形計(jì)算采用有限元方法求解結(jié)構(gòu)靜力方程,基于上述氣動(dòng)求解模型和結(jié)構(gòu)求解模型,采用松耦合方式,構(gòu)造了流固耦合求解器。首先研究了1g過載狀態(tài)下的某飛翼布局無人機(jī)靜氣動(dòng)彈性收斂時(shí)的結(jié)構(gòu)變形分布;其次,研究了靜氣動(dòng)彈性對(duì)該無人機(jī)總體氣動(dòng)性能及氣動(dòng)載荷重新分布的影響;最后對(duì)考慮靜氣動(dòng)彈性效應(yīng)的全機(jī)縱向和橫航向靜穩(wěn)定性等進(jìn)行了一定的研究。

1計(jì)算方法

1.1流體控制方程

可壓縮流的三維流體力學(xué)方程如下：

(1)

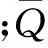
1.2結(jié)構(gòu)控制方程

本文使用Nastran軟件對(duì)有限元模型進(jìn)行靜力學(xué)求解,通用計(jì)算方程為:

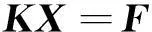
(2)

式中:K為剛度矩陣;X為結(jié)構(gòu)有限元節(jié)點(diǎn)位移列向量;F為結(jié)構(gòu)所受外載荷列向量。

1.3流體結(jié)構(gòu)耦合面插值

耦合CFD和CSD技術(shù)求解非線性氣動(dòng)彈性問題時(shí),需要在氣動(dòng)/結(jié)構(gòu)耦合面處進(jìn)行數(shù)據(jù)交換,包括:氣動(dòng)計(jì)算所得的氣動(dòng)力施加到結(jié)構(gòu)有限元節(jié)點(diǎn)上;結(jié)構(gòu)發(fā)生變形后,有限元節(jié)點(diǎn)的位移要反饋到耦合面上的氣動(dòng)網(wǎng)格節(jié)點(diǎn)上。

由于本文的研究對(duì)象為高空長航時(shí)大展弦比飛翼布局無人機(jī),結(jié)構(gòu)變形主要表現(xiàn)為展向的彎曲和扭轉(zhuǎn)變形,弦向變形相對(duì)較小,可以忽略不計(jì),因此這里引入機(jī)翼翼剖面不變形假設(shè)。結(jié)構(gòu)發(fā)生變形后,首先通過一系列機(jī)翼展向站位的彎曲和扭轉(zhuǎn)位移獲得變形后的幾何外形,然后重新生成氣動(dòng)網(wǎng)格進(jìn)行氣動(dòng)計(jì)算。此方法的優(yōu)點(diǎn)是避免了動(dòng)網(wǎng)格方法扭曲量過大而導(dǎo)致的氣動(dòng)載荷計(jì)算模塊計(jì)算精度降低的問題,同時(shí)又保證了附面層的計(jì)算精度等。

1.4計(jì)算流程

采用松耦合方式求解靜氣動(dòng)彈性的流程如圖1所示。

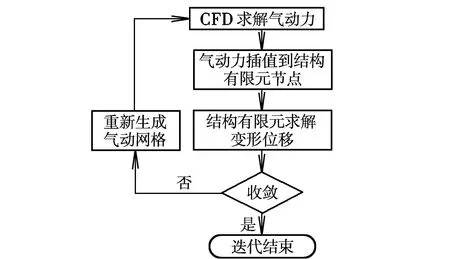
圖1　松耦合計(jì)算流程圖Fig.1　Loose coupling flow chart

文獻(xiàn)[8-10]利用松耦合流程進(jìn)行靜氣動(dòng)彈性求解時(shí),均假設(shè)機(jī)翼根部迎角保持不變,這種情況下最終解得的全機(jī)總載荷通常會(huì)發(fā)生變化,即改變了全機(jī)的過載系數(shù)。對(duì)于大展弦比后掠機(jī)翼,由于彎扭耦合效應(yīng),基于該假設(shè)解得的靜氣動(dòng)彈性收斂后的總載荷將小于原剛體外形計(jì)算所得載荷。而載荷重分布的另一種計(jì)算假設(shè)為:在飛機(jī)的總升力保持不變的條件下,求解載荷分布以及相應(yīng)的飛行迎角[11]。對(duì)于考慮靜氣動(dòng)彈性影響的飛機(jī),若要維持原有過載,必然要尋求新的飛行迎角,從而更便于研究恒定過載時(shí)飛機(jī)的靜氣動(dòng)彈性特性。因此,本文針對(duì)第二種情況選擇1g過載進(jìn)行研究。具體的計(jì)算不同之處在于:當(dāng)結(jié)構(gòu)變形計(jì)算完成后,為了保證總升力不變,需要尋找變形后的外形維持總升力不變所需的全機(jī)飛行迎角,由于本文研究的飛翼無人機(jī)的計(jì)算狀態(tài)始終處于線性升力段,通過迭代前后兩個(gè)迎角下的氣動(dòng)力計(jì)算結(jié)果便可線性插值出維持總升力不變所需的迎角;然后,計(jì)算此迎角下的氣動(dòng)載荷,并插值到結(jié)構(gòu)節(jié)點(diǎn)上進(jìn)行結(jié)構(gòu)計(jì)算,如此循環(huán)迭代,直至收斂。

2計(jì)算模型及結(jié)果分析

2.1氣動(dòng)模型

圖2為剛性飛機(jī)的CFD計(jì)算網(wǎng)格示意圖,其空間網(wǎng)格單元4 582 905個(gè),物面網(wǎng)格單元27 392個(gè)。初始計(jì)算狀態(tài)為自由來流Ma=0.6,飛行高度H=20 km,迎角α=3°,在氣彈耦合迭代求解的過程中進(jìn)行CFD計(jì)算時(shí),需要改變來流迎角來滿足總升力保持不變的前提。

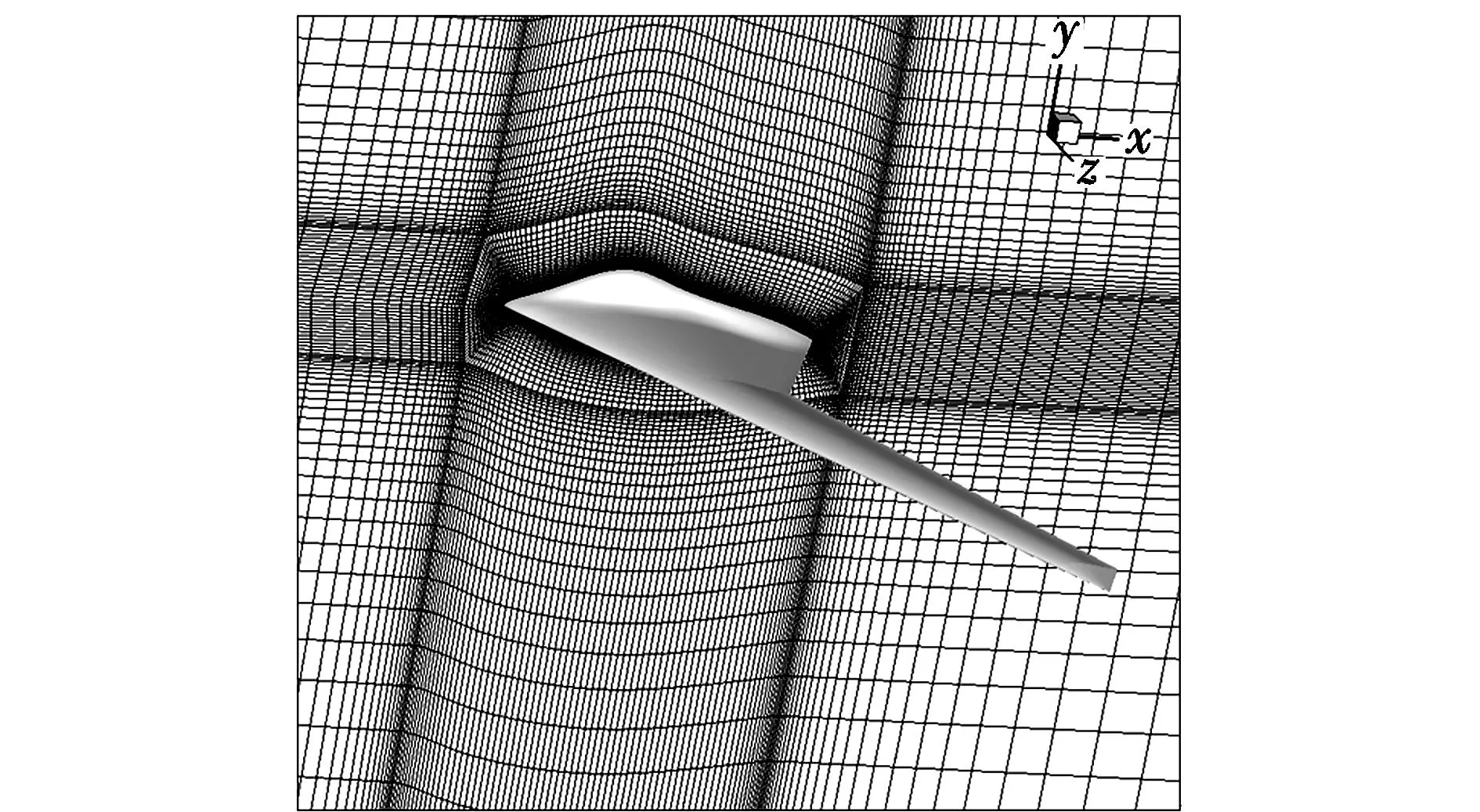
圖2　對(duì)稱面網(wǎng)格Fig.2　Grid of symmetry surface

2.2結(jié)構(gòu)模型

使用MSC.Patran建立飛翼結(jié)構(gòu)有限元模型時(shí),為了更真實(shí)地反映本文飛翼布局無人機(jī)的靜氣動(dòng)彈性特性,所建立的有限元模型考慮了翼身部分的進(jìn)氣道等細(xì)節(jié),外翼段精細(xì)有限元網(wǎng)格如圖3所示。

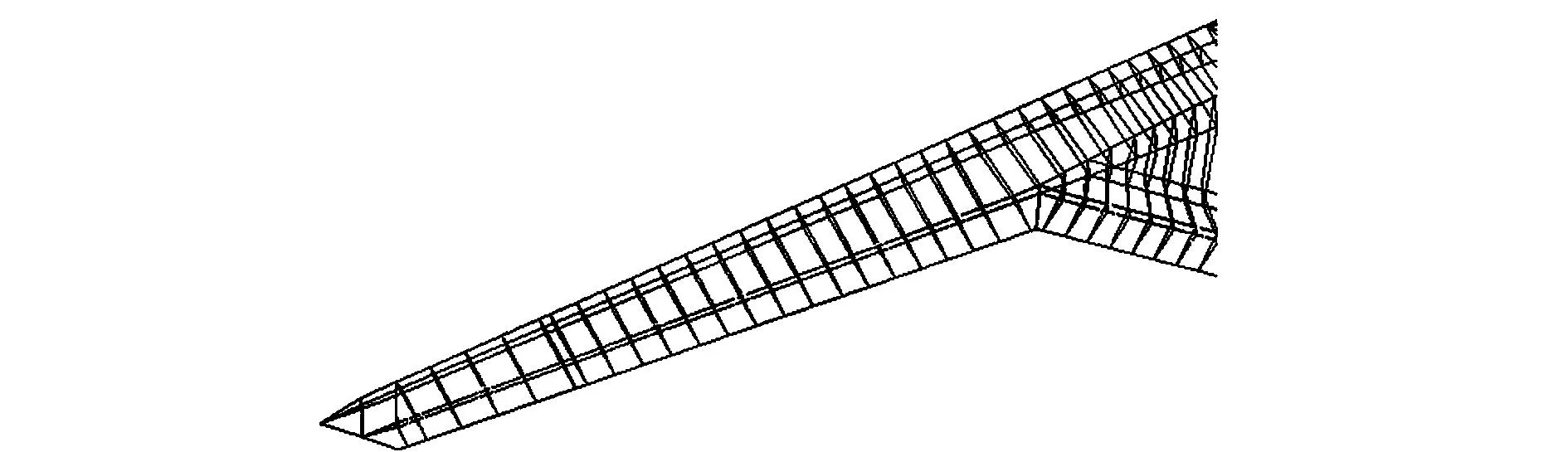
圖3　外翼段有限元網(wǎng)格Fig.3　Finite element grid of outer wing

2.3靜氣彈計(jì)算結(jié)果

1g過載下,經(jīng)過5個(gè)迭代步即可達(dá)到靜氣動(dòng)彈性求解收斂,收斂后的機(jī)翼展向彎曲和扭轉(zhuǎn)變形分布如圖4和圖5所示。在后文中,約定“1g”代表1個(gè)過載下發(fā)生靜氣彈變形后的外形,“rigid”代表未變形設(shè)計(jì)的剛體外形。

圖4　展向彎曲變形分布Fig.4　Spanwise deflection distribution

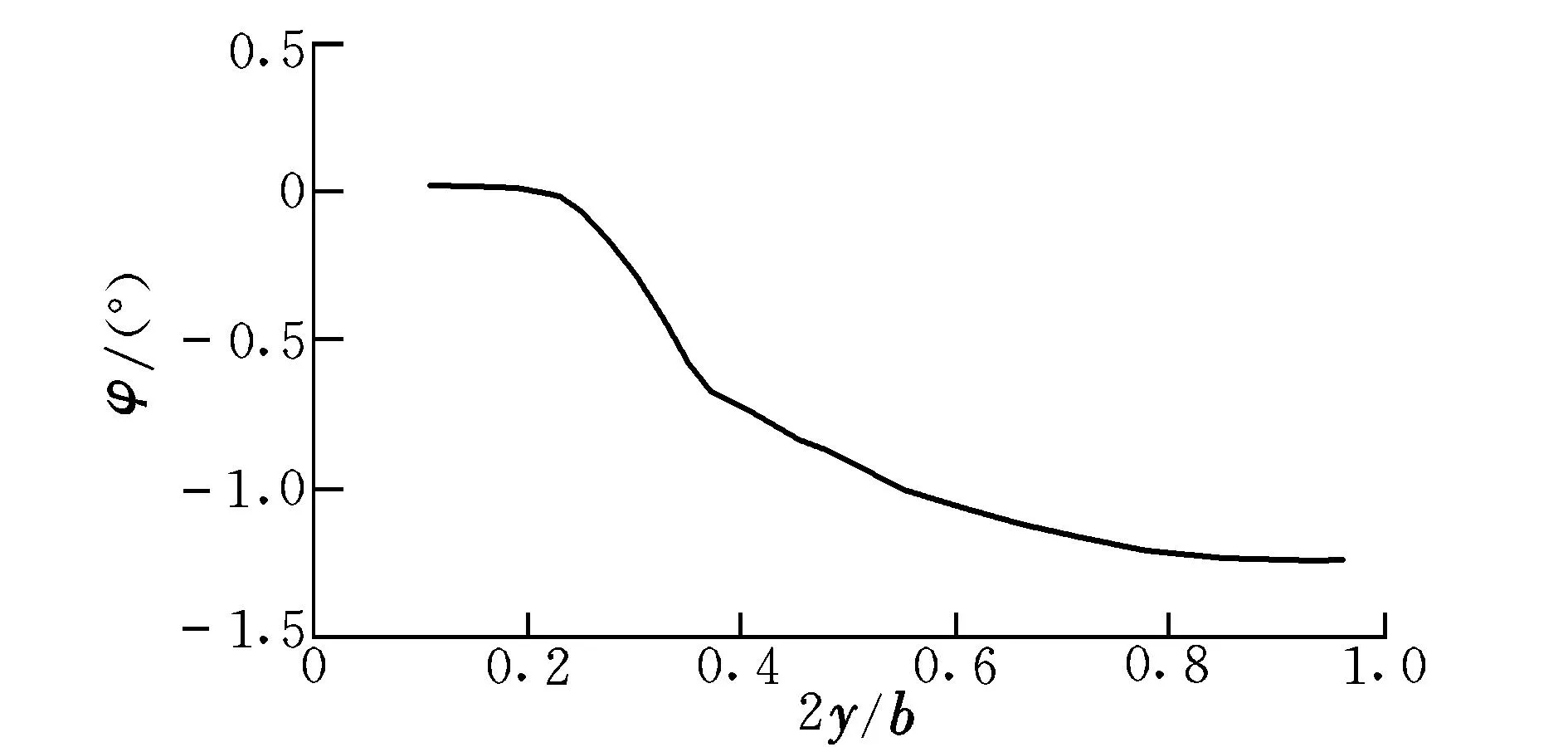
圖5　展向扭轉(zhuǎn)變形分布Fig.5　Spanwise twist angle distribution

本文剛性外形飛機(jī)的設(shè)計(jì)巡航迎角為3°,考慮氣動(dòng)彈性效應(yīng)后,經(jīng)過迭代計(jì)算,維持平飛所需的迎角將達(dá)到3.5°。飛機(jī)變形前后的氣動(dòng)特性對(duì)比如表1所示。可以看出:彈性變形前后升力系數(shù)誤差僅為0.39%,表明變形后仍然維持1g過載,但飛行迎角需要從3.0°增加到3.5°,并且變形后的全機(jī)升阻比減小了3.5%;設(shè)計(jì)剛體外形飛機(jī)在3°巡航時(shí),俯仰力矩系數(shù)接近0,基本滿足自配平,但彈性變形后將產(chǎn)生一個(gè)較大的抬頭力矩,需要偏轉(zhuǎn)相應(yīng)舵面進(jìn)行縱向力矩配平,這顯著偏離了原巡航設(shè)計(jì)點(diǎn),增加了配平阻力,將進(jìn)一步減小升阻比,從而顯著降低長航時(shí)無人機(jī)的巡航性能。

表1　變形前后氣動(dòng)特性比較

靜氣彈變形前后機(jī)翼沿展向的升力系數(shù)分布對(duì)比如圖6所示。

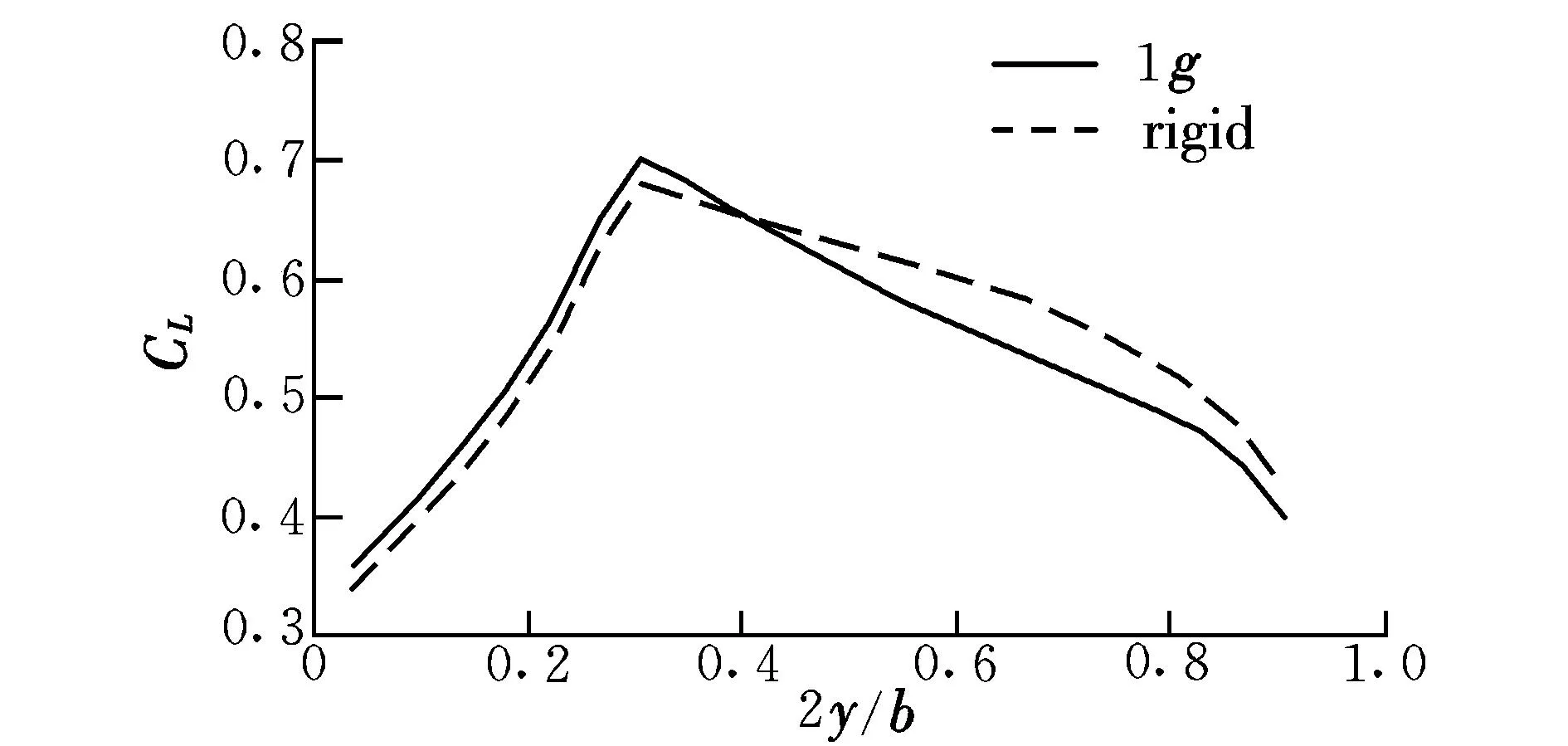
圖6　變形前后展向升力系數(shù)分布Fig.6　Spanwise lift coefficient distributionbefore and after deformation

可以看出:在內(nèi)翼段,變形前的升力系數(shù)要小于變形后的升力系數(shù);外翼段則相反,這是由于靜氣彈收斂后,外翼段有較大的負(fù)扭轉(zhuǎn)變形,從而降低了當(dāng)?shù)厣ο禂?shù)。而在本文靜氣彈求解迭代的過程中,始終保證總升力不變,為了補(bǔ)償彈性變形引起的升力損失,需要增加飛行迎角。內(nèi)翼段由于彈性扭轉(zhuǎn)角較小,總的作用效果相當(dāng)于增大了內(nèi)翼的有效迎角,因此內(nèi)翼段變形后的升力系數(shù)較大。總體來看,變形后的氣動(dòng)載荷體現(xiàn)出向翼根轉(zhuǎn)移的現(xiàn)象,對(duì)結(jié)構(gòu)受力特性是有利的。

如圖7所示,沿機(jī)翼展向取3個(gè)典型截面A,B,C。弦向壓力系數(shù)分布比較如圖8～圖10所示。

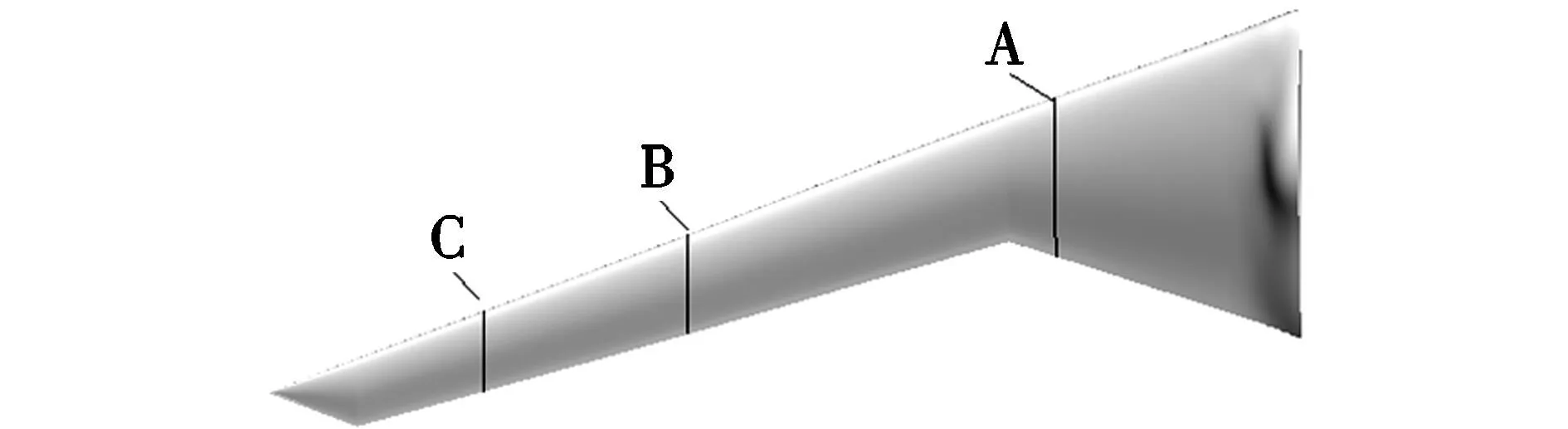
圖7　 截面站位示意圖Fig.7　Schematic of position of sections

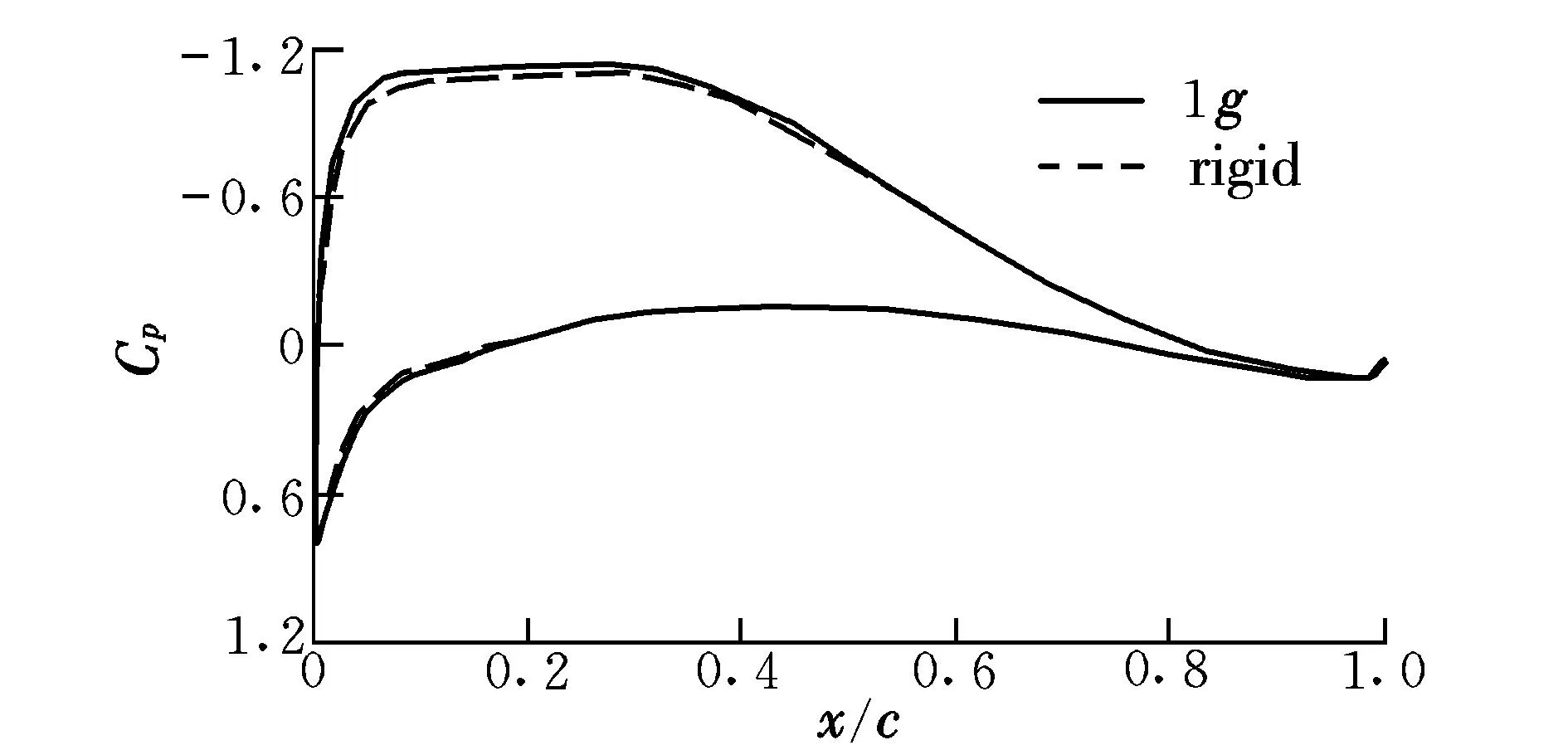
圖8　截面A壓力系數(shù)分布Fig.8　Section A pressure coefficient

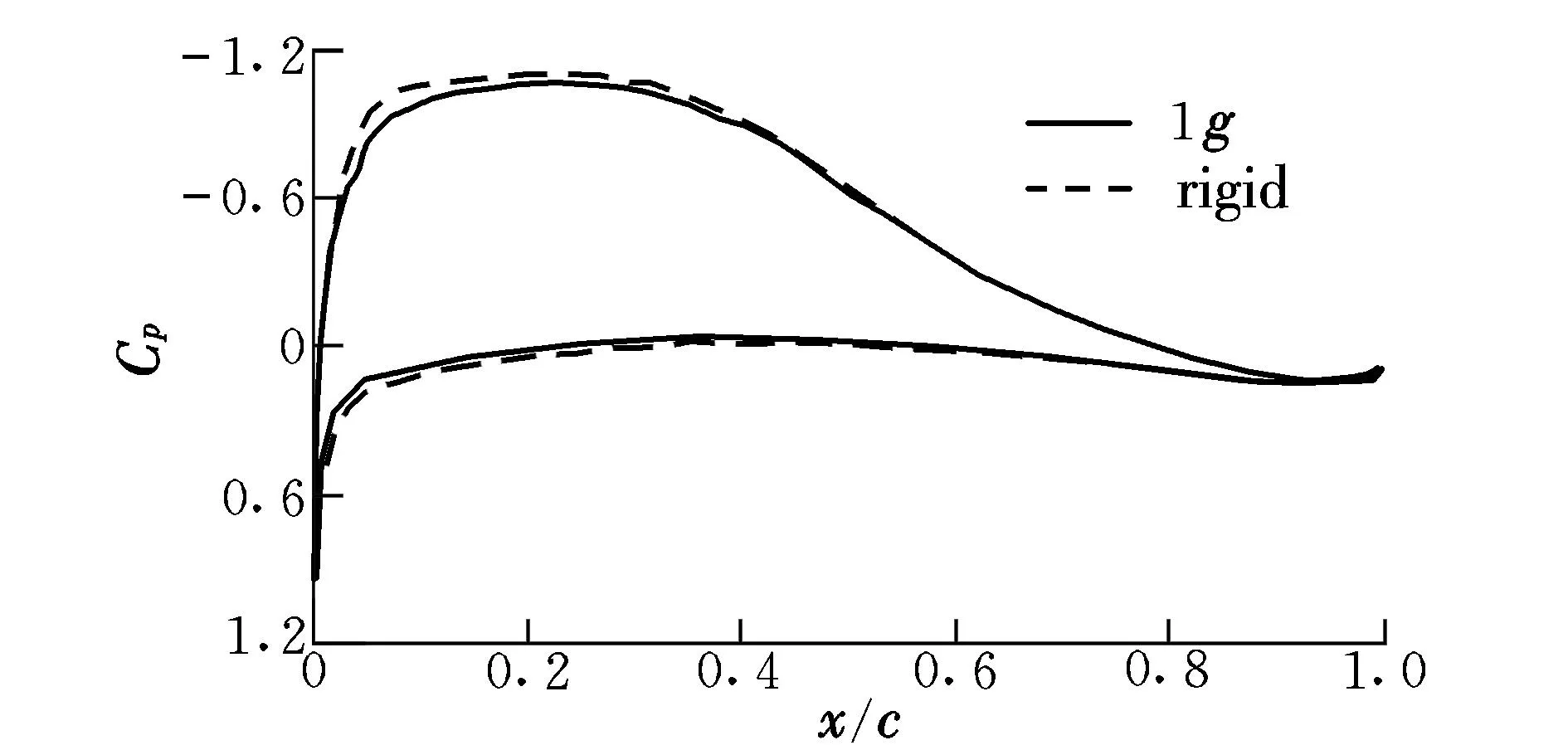
圖9　截面B壓力系數(shù)分布Fig.9　Section B pressure coefficient

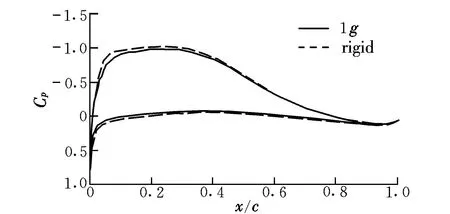
圖10　截面C壓力系數(shù)分布Fig.10　Section C pressure coefficient

從截面A壓力分布對(duì)比結(jié)果可以看出,變形后內(nèi)翼段剖面壓力系數(shù)積分面積變大,即截面升力系數(shù)變大;從外翼段的剖面B,C的壓力分布對(duì)比結(jié)果中可以看出,變形后壓力系數(shù)積分面積變小,即截面升力系數(shù)變小,這與圖6中展向升力系數(shù)分布得到的結(jié)論是一致的。

靜氣彈變形前后全機(jī)的升阻特性隨迎角的變化如圖11～圖13所示。可以看出:變形前后升力線斜率基本保持不變,但相同迎角下變形后的升力系數(shù)較變形前有一定的增量,其主要原因是氣彈變形后,機(jī)翼沿展向的各個(gè)剖面產(chǎn)生一定的負(fù)扭轉(zhuǎn),相當(dāng)于減小了飛翼無人機(jī)的零升迎角,從而使升力曲線下移,但對(duì)升力線斜率的影響較小;另外,靜氣彈變形也減小了全機(jī)的阻力,在α=3°時(shí)得到最大升阻比; 靜氣彈變形后,最大升阻比所對(duì)應(yīng)的迎角轉(zhuǎn)移到α=4°附近，并降低了全機(jī)的最大升阻比，偏離了總體氣動(dòng)性能設(shè)計(jì)指標(biāo)。

圖11　升力系數(shù)隨迎角變化曲線Fig.11　Variation of lift coefficient with angle of attack

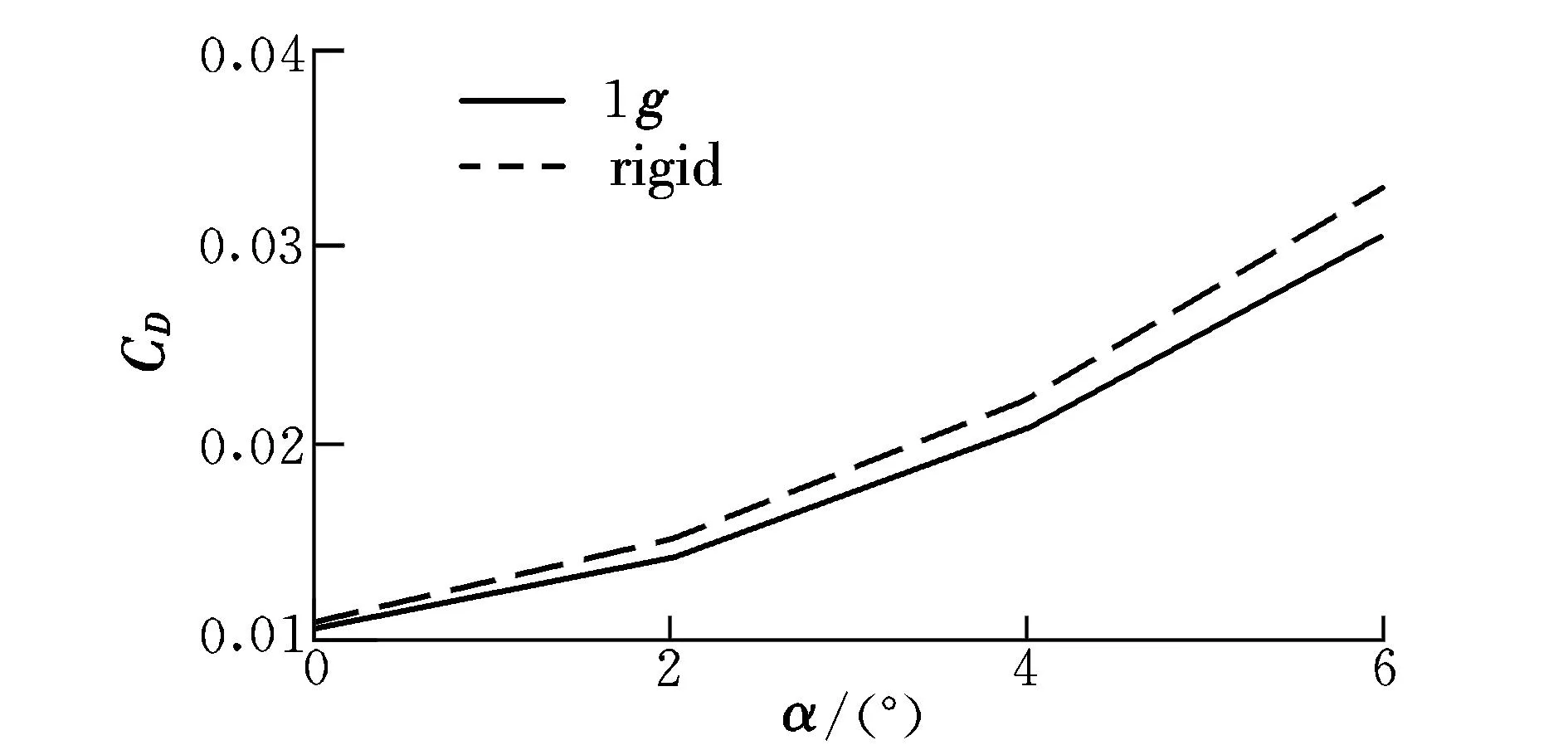
圖12　阻力系數(shù)隨迎角變化曲線Fig.12　Variation of drag coefficient with angle of attack

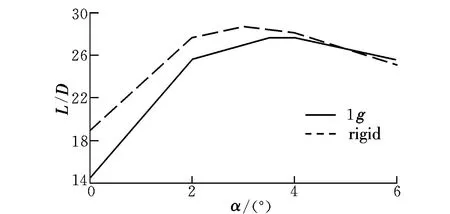
圖13　升阻比隨迎角變化曲線Fig.13　Variation of lift-drag ratio with angle of attack

圖14為變形前后縱向俯仰力矩系數(shù)隨迎角的變化曲線。可以看出:在迎角0°～6°的力矩線性段內(nèi),變形前后無人機(jī)均是縱向靜穩(wěn)定的,并且靜穩(wěn)定導(dǎo)數(shù)Cmα基本一致;但在相同迎角下,變形后較變形前產(chǎn)生了一個(gè)抬頭力矩增量,其主要原因是外翼段的升力作用于重心之后,而內(nèi)翼段升力作用于重心之前,但是外翼由于有更大的負(fù)扭轉(zhuǎn)角,因此損失的升力較內(nèi)翼要大,總的作用效果是產(chǎn)生一個(gè)抬頭力矩增量。從計(jì)算結(jié)果中還可以看出:剛性飛機(jī)設(shè)計(jì)外形在迎角6°～8°之間存在縱向靜不穩(wěn)定的現(xiàn)象,Cmα為0.012 30/(°),這是本文飛翼無人機(jī)存在的一個(gè)典型縱向靜不穩(wěn)定性問題[7];而發(fā)生氣彈變形后,迎角6°～8°雖然也是縱向靜不穩(wěn)定的,但Cmα減小為0.002 59/(°),有效緩和了剛性飛機(jī)設(shè)計(jì)外形的縱向靜不穩(wěn)定特性,從而有利于這類飛機(jī)的總體氣動(dòng)特性設(shè)計(jì)。

為了說明原因,取出8°迎角時(shí)典型截面B(截面位置同圖7)弦向壓力系數(shù)分布,如圖15所示。可以看出:在8°迎角時(shí),20%弦長附近形成激波,這是導(dǎo)致設(shè)計(jì)剛體外形縱向靜不穩(wěn)定的主要原因;而彈性變形后,激波后移,激波強(qiáng)度減弱,上表面弦向20%～60%存在更大的負(fù)壓值,使得截面合力作用點(diǎn)后移,從而減緩了設(shè)計(jì)剛體外形在6°～8°存在的縱向靜不穩(wěn)定特性。

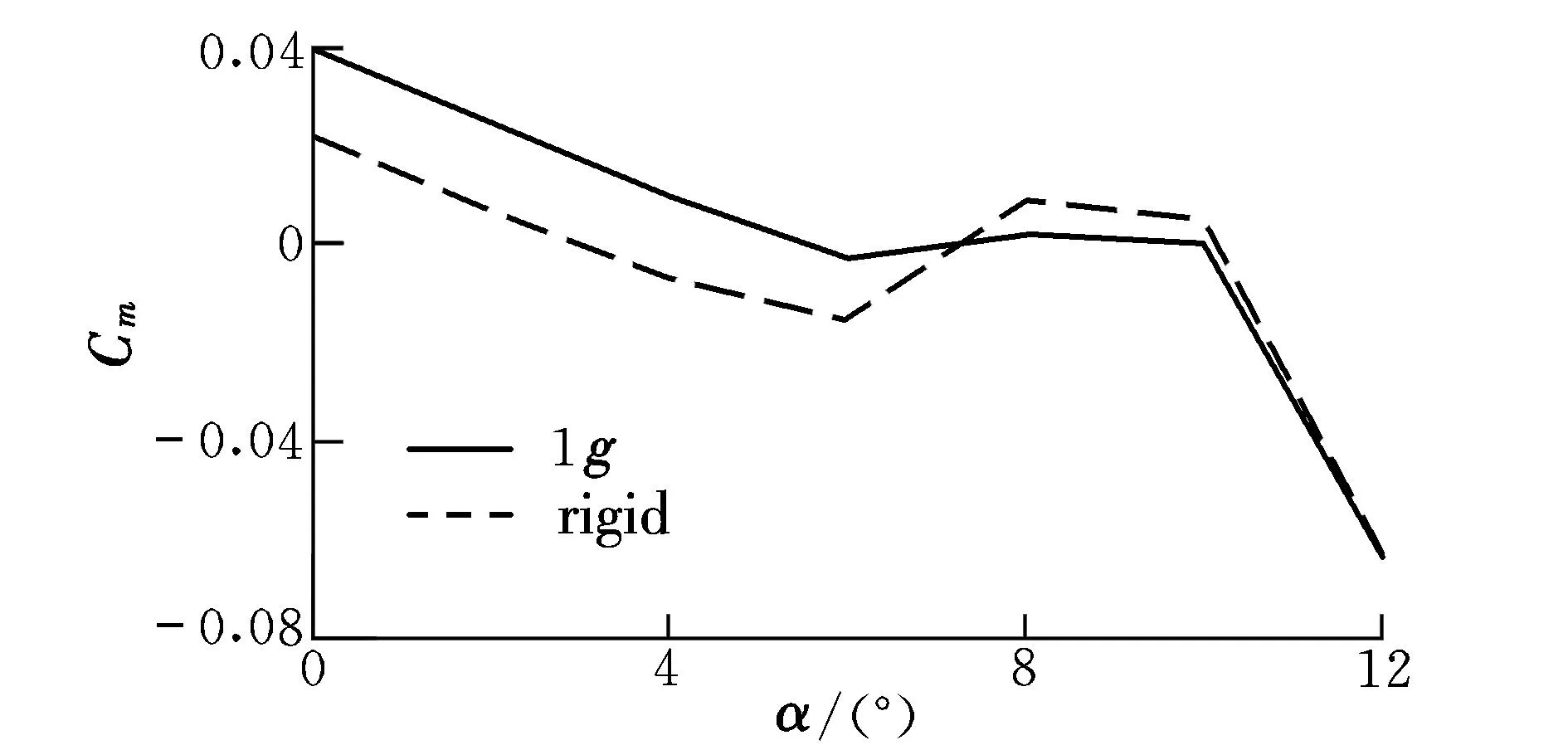
圖14　俯仰力矩系數(shù)隨迎角變化曲線Fig.14　Variation of pitch moment coefficient with angle of attack

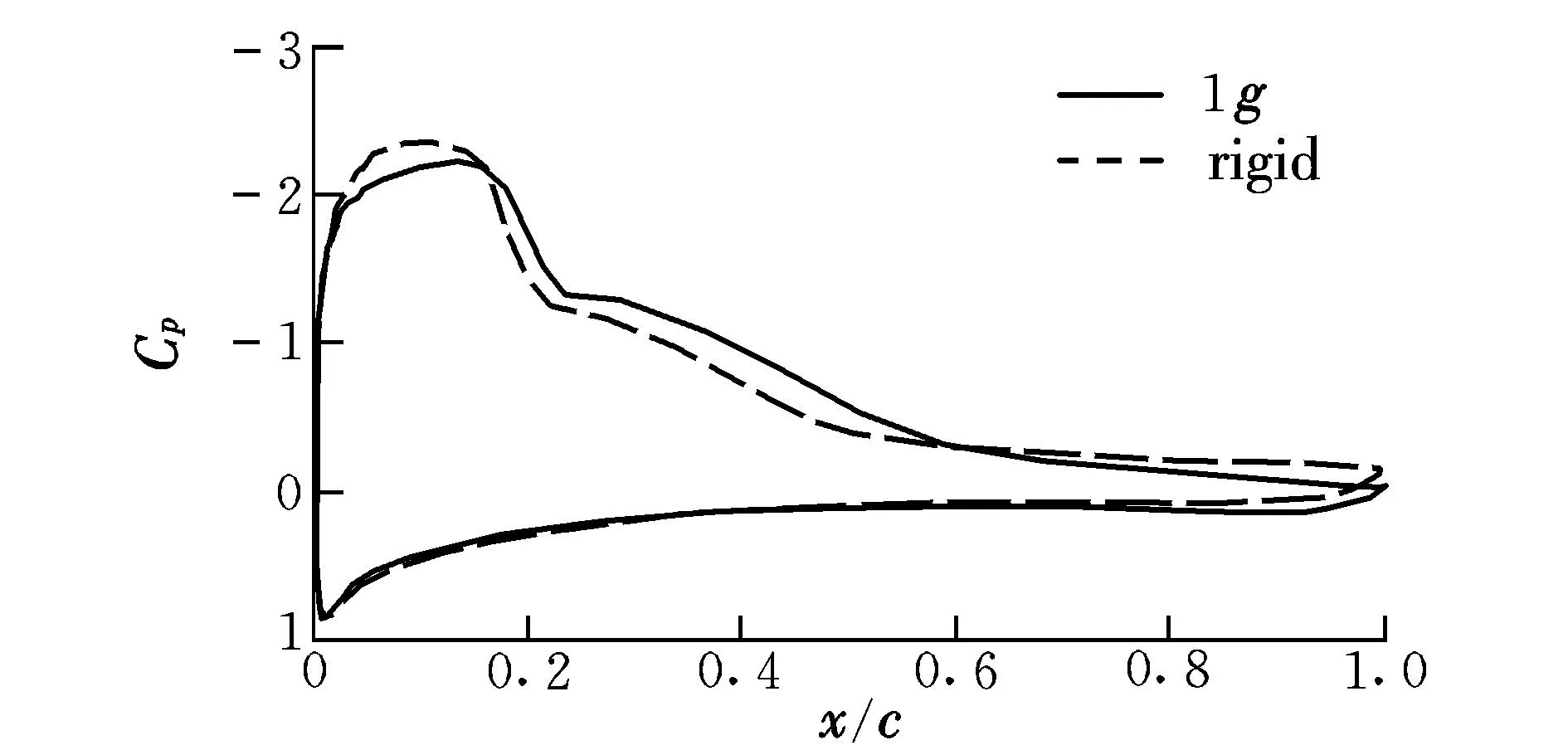
圖15　截面B壓力系數(shù)分布(α=8°)Fig.15　Section B pressure coefficient(α=8°)

靜氣彈變形前后全機(jī)的橫航向氣動(dòng)特性如圖16和圖17所示。從圖16可以看出:變形后,橫向靜穩(wěn)定導(dǎo)數(shù)增加了41.7%,這是因?yàn)轱w翼布局無人機(jī)的橫向穩(wěn)定性主要由機(jī)翼的后掠角和上反角決定;而發(fā)生氣彈變形后,外翼段所產(chǎn)生的彎曲變形相當(dāng)于增大了機(jī)翼的上反角,因此有效地改善了橫向靜穩(wěn)定性。

從圖17可以看出,飛翼無人機(jī)由于缺少垂尾,并且機(jī)身較扁平,因此先天具有航向靜穩(wěn)定性不足的特點(diǎn),彈性變形沒有給航向靜穩(wěn)定特性帶來改善,而是使飛翼更接近中立穩(wěn)定,這主要是因?yàn)橥庖矶蔚膹澢冃问沟猛庖矶蔚纳υ陲w翼平面內(nèi)產(chǎn)生分量,進(jìn)而對(duì)重心形成偏航力矩,飛翼右側(cè)滑時(shí),由于右側(cè)機(jī)翼的升力大于左側(cè)機(jī)翼,總的作用效果為產(chǎn)生負(fù)的偏航力矩,因此削弱了飛翼的航向靜穩(wěn)定性。

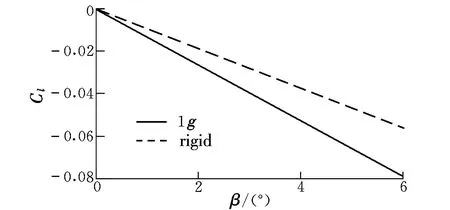
圖16　滾轉(zhuǎn)力矩系數(shù)隨側(cè)滑角變化曲線Fig.16　Variation of roll moment coefficient

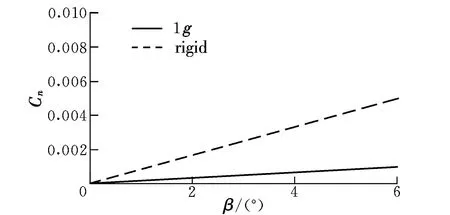
圖17　偏航力矩系數(shù)隨側(cè)滑角變化曲線Fig.17　Variation of yaw moment coefficient

3結(jié)論

本文基于CFD/CSD松耦合求解技術(shù),對(duì)某高空長航時(shí)飛翼布局無人機(jī)在1g過載下的靜氣動(dòng)彈性特性進(jìn)行了研究,得到以下結(jié)論:

(1)大展弦比高空長航時(shí)飛翼布局無人機(jī)的靜氣動(dòng)彈性效應(yīng)降低了全機(jī)的升阻比性能,同時(shí)偏離了原巡航力矩配平點(diǎn),引入較大的抬頭力矩;氣動(dòng)載荷的重新分布向翼根轉(zhuǎn)移,從而有利于結(jié)構(gòu)設(shè)計(jì)。

(2)靜氣動(dòng)彈性變形不但有效緩和了剛性設(shè)計(jì)外形下存在的縱向靜不穩(wěn)定現(xiàn)象,從而改善了縱向靜穩(wěn)定性，而且還顯著改變了全機(jī)的橫航向穩(wěn)定性導(dǎo)數(shù),特別是Clβ/Cnβ的變化決定著橫航向飛行品質(zhì)。因此，在這類飛機(jī)的總體設(shè)計(jì)中應(yīng)充分考慮氣彈效應(yīng)帶來的影響。

(3)高空長航時(shí)大展弦比飛翼布局無人機(jī)在總體氣動(dòng)設(shè)計(jì)時(shí)一般采用“單設(shè)計(jì)點(diǎn)”的氣動(dòng)設(shè)計(jì)思想,即在預(yù)定的設(shè)計(jì)狀態(tài)下其氣動(dòng)性能非常好,但略微偏離該設(shè)計(jì)狀態(tài)時(shí)可能出現(xiàn)顯著的性能降低。若不考慮氣動(dòng)彈性效應(yīng),真實(shí)飛行狀態(tài)將嚴(yán)重偏離設(shè)計(jì)狀態(tài),從而顯著影響全機(jī)的總體氣動(dòng)性能。

參考文獻(xiàn)：

[1]Bolsunovsky A L,Buzoverya N P,Gurevich B I,et al.Flying wing:problems and decisions[J].Aircraft Design,2001(4):193-219.

[2]范銳軍,馮朝輝,周洲.大展弦比無人機(jī)的靜氣彈問題計(jì)算及分析[J].力學(xué)季刊,2009,30(4):548-554.

[3]陳大偉,楊國偉.靜氣動(dòng)彈性計(jì)算方法研究[J].力學(xué)學(xué)報(bào),2009,41(4):469-479.

[4]安效民,徐敏,陳士櫓.多場耦合求解非線性氣動(dòng)彈性的研究綜述[J].力學(xué)進(jìn)展,2009,39(3):284-298.

[5]Smith M J,Hodges D H.Evaluation of computational algorithms suitable for fluid-structure interactions[J].Journal of Aircraft,2000,37(2):282-294.

[6]Yang C,Loehner R.Numerial simulation of a maneuvering missile using a loose fluid-structure coupling algorithm[R].AIAA-97-0408,1997.

[7]李盈盈.綜合全機(jī)氣動(dòng)特性的飛翼布局進(jìn)排氣設(shè)計(jì)研究[D].西安:西北工業(yè)大學(xué),2014.

[8]王軍利.飛翼布局無人機(jī)非定常流場及氣動(dòng)彈性研究[D].西安:西北工業(yè)大學(xué),2011.

[9]劉艷,白俊強(qiáng),華俊,等.基于RBF插值技術(shù)的CFD/CSD非線性耦合分析方法研究[J].計(jì)算力學(xué)學(xué)報(bào),2014,31(1):120-127.

[10]張華,馬東立,馬鐵林.彈性變形對(duì)柔性機(jī)翼氣動(dòng)特性影響[J].北京航空航天大學(xué)學(xué)報(bào),2008,34(5):487-490.

[11]陳桂彬,楊超,鄒叢青.氣動(dòng)彈性設(shè)計(jì)基礎(chǔ)[M].北京:北京航空航天大學(xué)出版社,2010:26-28.

(編輯：崔立峰)

Study on static aeroelasticity of high altitude long endurance flying wing UAV

ZHANG Qiang1, ZHU Xiao-ping2, ZHOU Zhou1, WANG Wei1

(1.School of Aeronautics, NWPU, Xi’an 710072, China;2.No.365 Research Institute, NWPU, Xi’an 710065, China)

Abstract:High altitude long endurance high-aspect ratio flying wing will undergo large deformation, which will significantly change characteristics of lift and drag as well as static stability. Therefore, conventional rigid aircraft assumption cannot meet the accuracy requirements of the aerodynamic analysis of this type of aircraft. In this paper, based on CFD/CSD coupling, static aeroelasticity of high aspect ratio flying wing was studied. The results show that static aeroelastic effect will significantly reduce the lift drag ratio and increase pitching moment at designed cruise trimming point;On the other hand, lateral static stability derivative will be increased by 41.7%, and the longitudinal instability inherent in the flying wing will be improved. The aerodynamic loads move towards the wing root after aeroelastic deformation, which is advantageous to the structural design.

Key words:flying wing UAV; static aeroelasticity; CFD/CSD coupling; lift drag ratio; static stability

中圖分類號(hào)：V211.47

文獻(xiàn)標(biāo)識(shí)碼：A

文章編號(hào)：1002-0853(2016)01-0040-06

作者簡介:張強(qiáng)(1991-)，男，山東濰坊人，碩士研究生，研究方向?yàn)轱w行器氣動(dòng)彈性。

收稿日期:2015-04-17;

修訂日期:2015-06-05; 網(wǎng)絡(luò)出版時(shí)間:2015-09-18 09:47