基于局部均值分解的直流電機換向電流分析

姬少龍，季寶杰，李觀文，李建鋒

(1.河南農業大學， 鄭州 450002；2.96520部隊，洛陽 471000；3.防空兵學院，鄭州 450052)

基于局部均值分解的直流電機換向電流分析

姬少龍1，季寶杰1，李觀文2，李建鋒3

(1.河南農業大學， 鄭州 450002；2.96520部隊，洛陽 471000；3.防空兵學院，鄭州 450052)

提出了基于局部均值分解(local mean decomposition, LMD)的直流電機換向電流分析新方法。首先，運用LMD將起動時的電樞電流分解成系列乘積函數(Product Function, PF)與剩余分量之和；其次，定義了相鄰PF相關系數這一概念，并據此確定組成換向電流和直流成分的PF階數；最后，對換向電流進行基于LMD的能量譜分析，可獲取換向電流的能量-時間-頻率的三維關系圖。相關仿真和實驗結果表明了所提方法的正確性。

換向電流；局部均值分解；乘機函數；相關系數；能量譜

0 引 言

直流電機的換向性能是衡量其優劣的重要指標，換向不良可能引起噪聲、火化等諸多難題，尤其是對于新能源汽車，換向不良甚至會引起電磁干擾[1-3]。由于換向是一個復雜的物理和化學過程，目前難以用解析數學的方法精確描述換向電流，而換向電流的瞬時幅頻信息與換向性能密切相關[4-5]。

根據換向電流頻率與轉速成比例關系，可以實現直流電機無轉速傳感器間接測速[6-10]。主要研究如何提取換向電流及求其頻率，而忽略了換向電流的幅值和能量信息。由于小波缺乏自適應性并受Heisenberg的限制，文獻[6]和文獻[7]分別運用經驗模態分解(Empirical Mode Decomposition，EMD)和局部均值分解(Local Mean Decomposition，LMD)獲取換向電流，自適應性較好[11]，但缺乏EMD和LMD的對比研究；而且在選擇固有模態函數(Intrinsic mode function，IMF)和乘積函數(Product function，PF)獲取換向電流時，僅根據人工經驗，缺乏相應的分析。

針對以上不足，本文根據噪聲、換向電流及直流分量的相關性，確定了PF的階數，以獲取換向電流，然后運用基于LMD的能量譜，給出換向電流的幅值/能量-時間-頻率的三維關系，為研究直流電機換向性能提供了一種新的途徑。

1 LMD和基于LMD的換向電流能量譜

1.1 LMD原理

LMD可將復雜信號按頻率從高到低的順序依次分解成系列PF分量之和，且PF分量屬于調幅-調頻函數x(t)。對任一函數x(t)，基于LMD的分解方法[11-13]：

(1) 求取x(t)所有的局部極值點ni，然后對相鄰的局部極值點做平均，得到局部均值mi，即：

(1)

用折線將所有的局部均值點相連，經滑動平均算法平滑可獲取局部均值信號m11(t)。

(2)根據局部極值點得估計包絡值ai：

(2)

用折線將包絡估計值相連，經滑動平均算法平滑可獲取包絡估計信號a11(t)。

(3)用原始的x(t)減去局部均值信號m11(t)，可獲函數h11(t)：

(3)

(4)通過函數h11(t)與函數a11(t)的比值獲取調頻函數，則調頻函數s11(t)：

(4)

通過對s11(t)運行以上步驟，獲取函數s11(t)的估計包絡信號a12(t)。當a12(t)不為1時，表明s11(t)不屬于純調頻函數，則對以上迭代步驟重復n次，直到s1n(t)屬于純調頻函數。此時，包絡估計信號a1(n+1)(t)=1，即：

(5)

(6)

終止迭代條件如下：

(7)

為加快計算速度，往往設定一個誤差量Δe，當1-Δe≤a1n(t)≤1+Δe時，終止迭代。

(5) 將全部包絡估計函數相乘可得包絡函數a1(t)：

(8)

(6)原始信號x(t)的第一個PF分量可通過包絡函數a1(t)與純調頻函數s1n(t)相乘得到：

(9)

首先分離出的PF1頻率最高，屬于調幅-調頻函數，包絡函數a1(t)是它的瞬時幅值，由純調頻函數s1n(t)可求出其瞬時頻率f1(t)，則：

(10)

(7)用原始信號x(t)減去PF1，得函數c1(t)，令c1(t)當作新的函數，運行以上步驟并重復k次，當ck(t)屬于單調函數終止。

(11)

原始信號可由所有PF分量和ck(t)重構，即：

(12)

1.2 基于LMD換向電流能量譜

由式(12)可知，對任一復雜函數可用系列PF和一個剩余分量之和表示，結合式(9)和式(10)知，信號x(t)可由下式表示[14]：

(13)

式中：m為PF分量的個數；ap(t)表示相應PF的瞬時幅值；fp(t)為相應PF的瞬時頻率；這里剩余分量被忽略。

在式(13)中，乘積函數的瞬時幅值和瞬時頻率均是時間的函數，這一特性和Hilbert譜中的瞬時幅值、頻率很相似[15]。基于此，定義信號x(t)基于局部均值分解的時頻分布曲線為S(f，t)，則有：

(14)

S(f，t)體現了信號幅值、頻率和時間關系。

繼續定義每一個乘積函數的能量，則有：

(15)

式(15)描述了信號能量隨時間的變化關系，所以，信號基于局部均值分解的能量譜可定義：

(16)

S2(f,t)定量描述了信號能量的時頻分布關系。由于直流電機空載起動信號經LMD后，按頻率從高到低的順序分離出PF分量。而采集直流電機起動電流含有高頻噪聲、換向電流和直流分量，且其頻率從高到低的順序排列，要得到換向電流的幅值/能量與頻率和時間的分布關系，只考察換向電流對應的PF即可，因此定義基于局部均值分解的換向電流能量譜：

(17)

式中：n1，n2表示提取換向電流所需PF分量的階數，其滿足1≤n1≤n2≤m，S’2反映了換向電流的能量隨頻率和時間的變化關系，定量描述換向電流的幅值/能量與頻率和時間的關系，為考察換向性能提供了一種依據。

2 仿真電流分析

忽略換向時，由電機學知識，直流電機空載起動時電流可用下式表示：

(18)

式中：Ist為起動電流；Ia為穩態電流；Tst為電機時間常數。

換向電流還沒有定量公式[3]，文獻[7]實驗結果表明換向電流是調頻-調幅函數。所以可用下式的調頻-調幅函數表示換向電流，以對比EMD和LMD分析換向電流時的優劣。

(19)

式中：I0為起動瞬間的換向電流值；Ih為穩態時的換向電流；Tst1，Tst2分別為起動換向電流幅值衰減系數和頻率變化系數。

考慮換向效應時的起動電流可由上述兩種電流疊加得到。取Ist=1.717 A，Ia=0.17 A，Tst=0.1 s；I0=0.24 A，Tst1=0.083 s，Ih=0.04 A，Tst2=0.105 s，A0=0.1，f=375 Hz。得到的仿真電流如圖1所示。

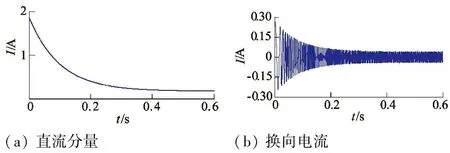
(a)直流分量(b)換向電流

(c) 起動電流

分別運用EMD和LMD對圖1的起動電流進行分解，所得結果如圖2所示。

從圖2可知，LMD和EMD都將仿真的起動電流分解為兩個分量和一個剩余分量之和。PF1和IMF1高度吻合，其波形和理論上的換向電流相似，可認為是換向電流；分別將PF2和IMF2分別與對應的剩余分量和殘差相加可獲取直流電流。

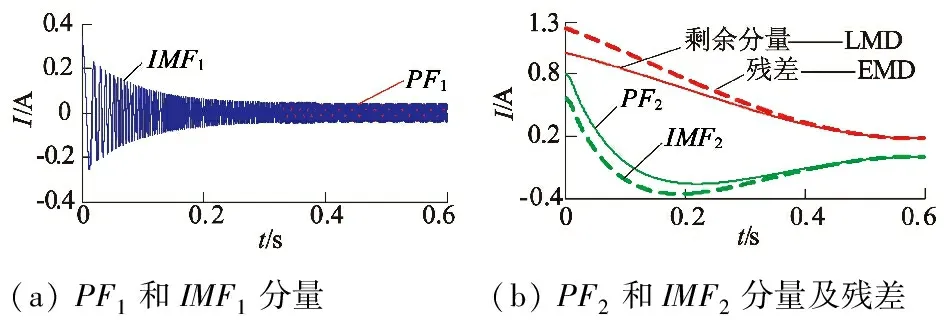
(a)PF1和IMF1分量(b)PF2和IMF2分量及殘差

圖2 基于LMD和EMD的起動電流分解結果

理論上的換向電流和直流分量以及分別運用LMD和EMD提取得換向電流及直流分量如圖3所示。從圖3可知，運用LMD提取換向電流及直流電流時的效果與EMD一樣，幾乎和理論上的仿真電流重合，說明LMD在分解效果上可與EMD相媲美。

瞬時幅值和瞬時頻率是換向電流的重要特征，根據式(8)和式(10)可得換向電流的幅值及其頻率；另外，本文對比了希爾伯特黃變換(Hilbert-Huang Transformer,HHT)中應用Hilbert變換的方法獲取換向電流的瞬時特征，相應的對比圖如圖4所示。由圖4可知，HHT處理效果在端點處較差，主要是HHT中的Hilbert變換存在“邊際飛翼”現象；而LMD獲取瞬時幅值及頻率時運用了滑動平均算法，所以在端點處的效果較好。而且HHT方法在求取頻率時出現了難以解釋的負頻率現象。另外，HHT“篩分”停止條件采用Rilling提出的準則[16]，LMD中取Δe=0.001，在相同條件下，從分解仿真的起動電流到獲取換向電流的瞬時幅值和瞬時頻率曲線，LMD方法僅需0.909 820 s，而HHT方法耗時2.082 915 s。由此可知，較之HHT，LMD分析起動電流時具有較快的運算速度。究其原因：一是LMD在“篩分”過程中采用除法運算，而HHT運用減法運算，獲取一個PF分量時，LMD的“篩分”次數較少；二是HHT求取換向電流瞬時特征時，需用Hilbert變換及其逆變換，將瞬時特征求取變換到虛數領域進行，耗時較多。

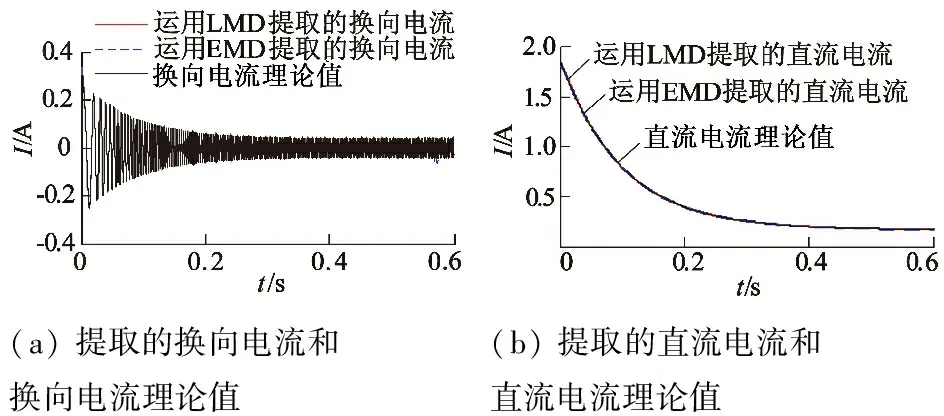
(a)提取的換向電流和換向電流理論值(b)提取的直流電流和直流電流理論值

圖3 換向電流、直流電流及其理論曲線對比圖

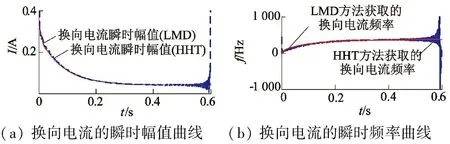
(a)換向電流的瞬時幅值曲線(b)換向電流的瞬時頻率曲線

圖4 換向電流的瞬時幅值和瞬時頻率曲線

由換向電流的瞬時幅值和瞬時頻率，根據式(17)可得基于LMD的換向電流能量譜；相應地，根據HHT獲取的換向電流瞬時幅值和瞬時頻率，可得換向電流的Hilbert能量譜，如圖5所示。由圖5可知，LMD方法的聚集性較好，而HHT方法獲取的換向電流能量譜在端點處存在發散。

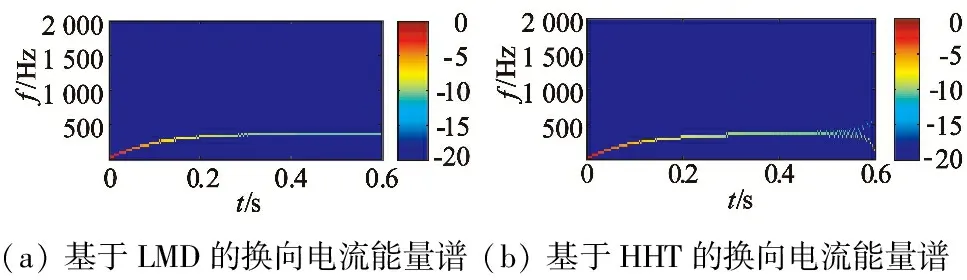
(a)基于LMD的換向電流能量譜(b)基于HHT的換向電流能量譜

圖5 換向電流能量譜

3 案例分析

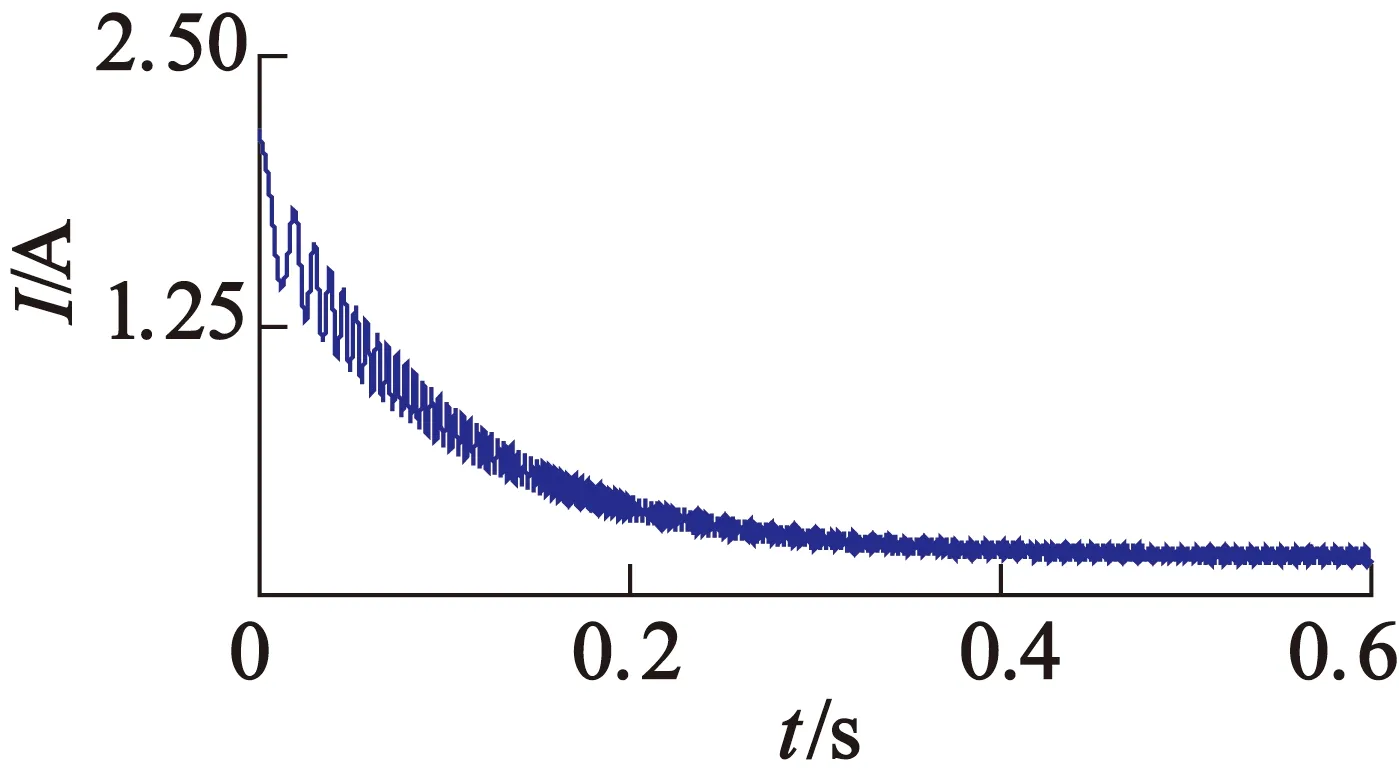
信號采集及其連接如圖6所示，它由數據采集卡ARTUSB2850、霍爾電流傳感器LSTR25N、 PC和電磁式并勵直流電機組成。直流電機的額定功率PN=185 W，額定電流IN=1.1 A，額定電壓UN=220 V，額定轉速為1 600 r/min。其極對數為1，換向片數為44片，采集的電流如圖7所示(采樣頻率為20 kHz)。

圖6 現場實驗設備及其連接

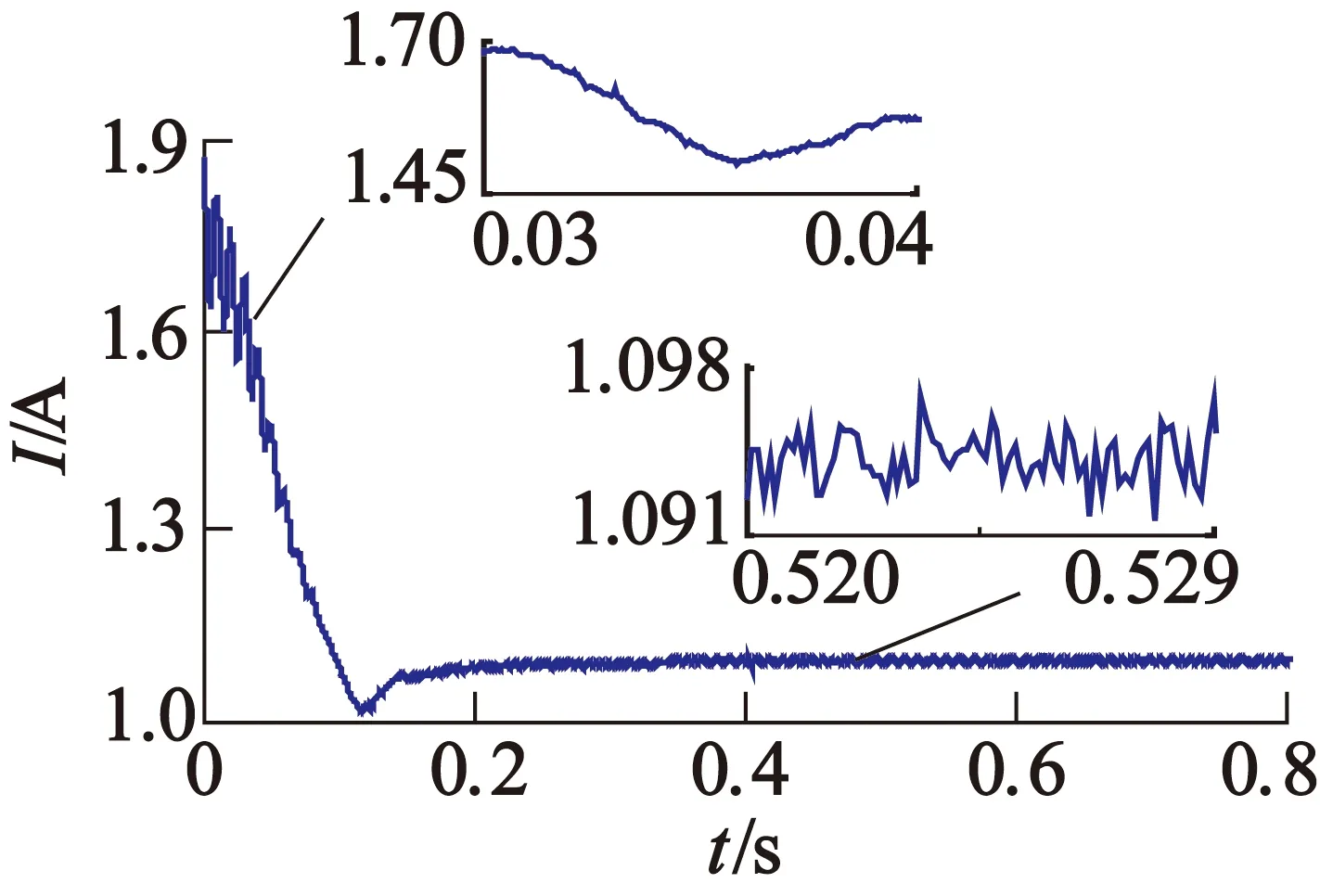
圖7 起動時的電樞電流

運用LMD可將起動時的電樞電流分解成一個剩余分量與系列PF分量，如圖8所示。

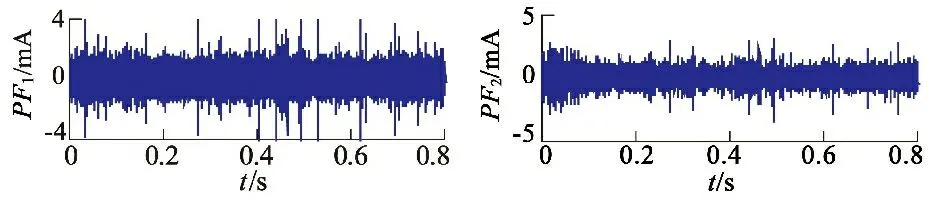
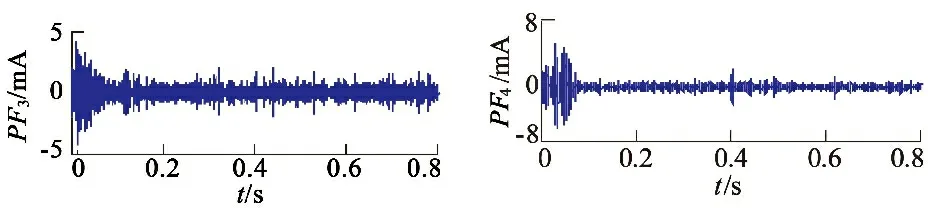
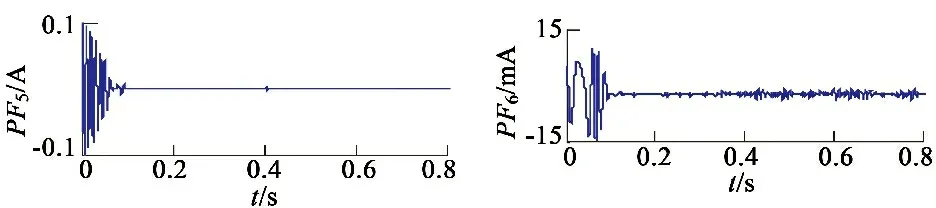
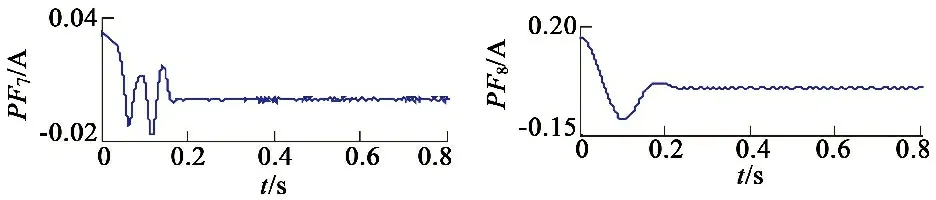
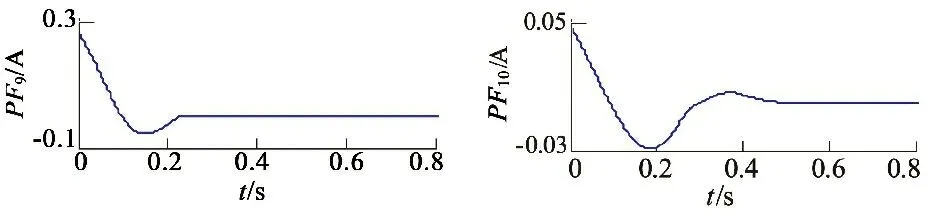
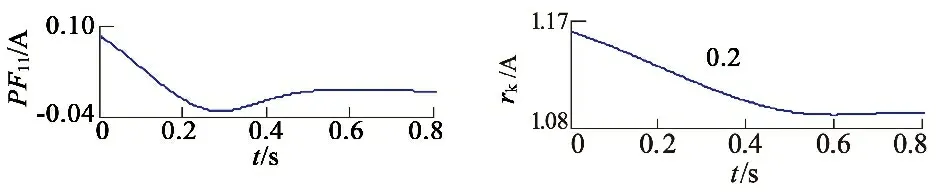
圖8 起動電流基于LMD的分解結果

由圖8可知，LMD將起動電流按頻率從高到低的順序分離出PF分量，以往文獻常根據經驗選擇PF分量提取換向電流和直流電流[6-7]。由于換向電流和直流成分頻率明顯不同，換向電流和直流成分分別被分解成幾個不同PF分量，組成換向電流的PF分量和組成直流成分的PF分量分別具有較強的相關性，而隨機噪聲相關性較差。基于以上特點，本文考察相鄰PF分量的相關系數，確定PF的階數組成換向電流和直流成分。

定義相鄰PFi和PFi+1的相關系數：

(20)

式中：n為PF分量的數據序列長度；PFi表示相應的PF分量。

圖8中相鄰PF分量的相關系數如圖9所示。

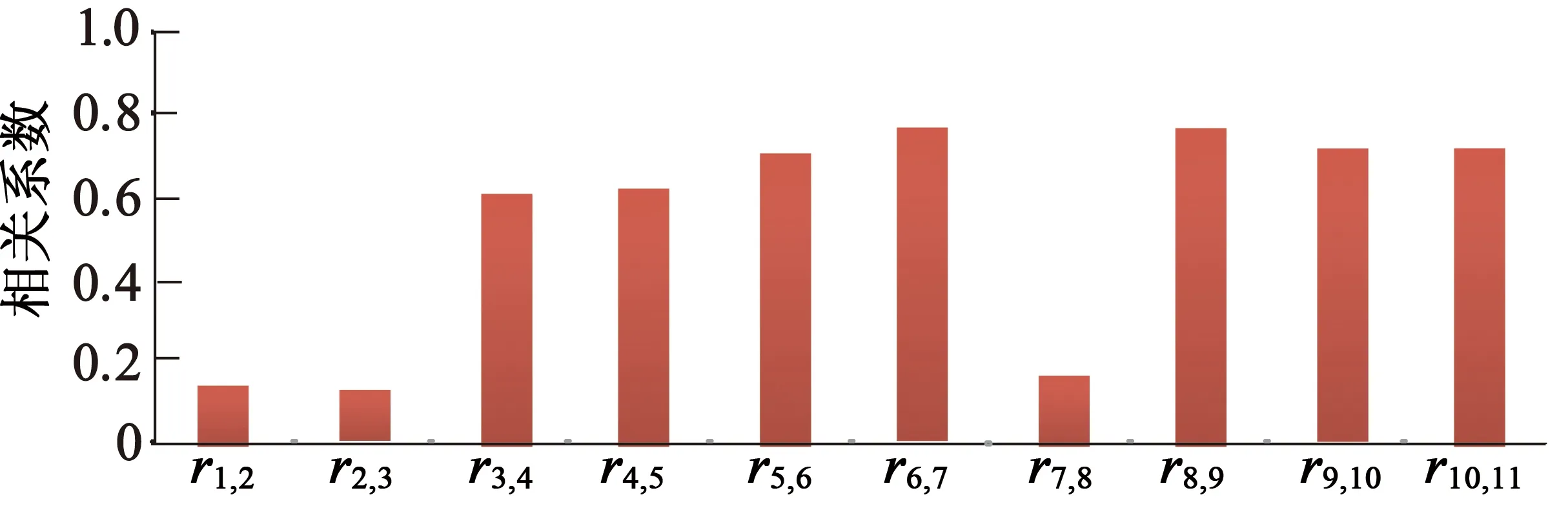
圖9 相鄰PF分量的相關系數

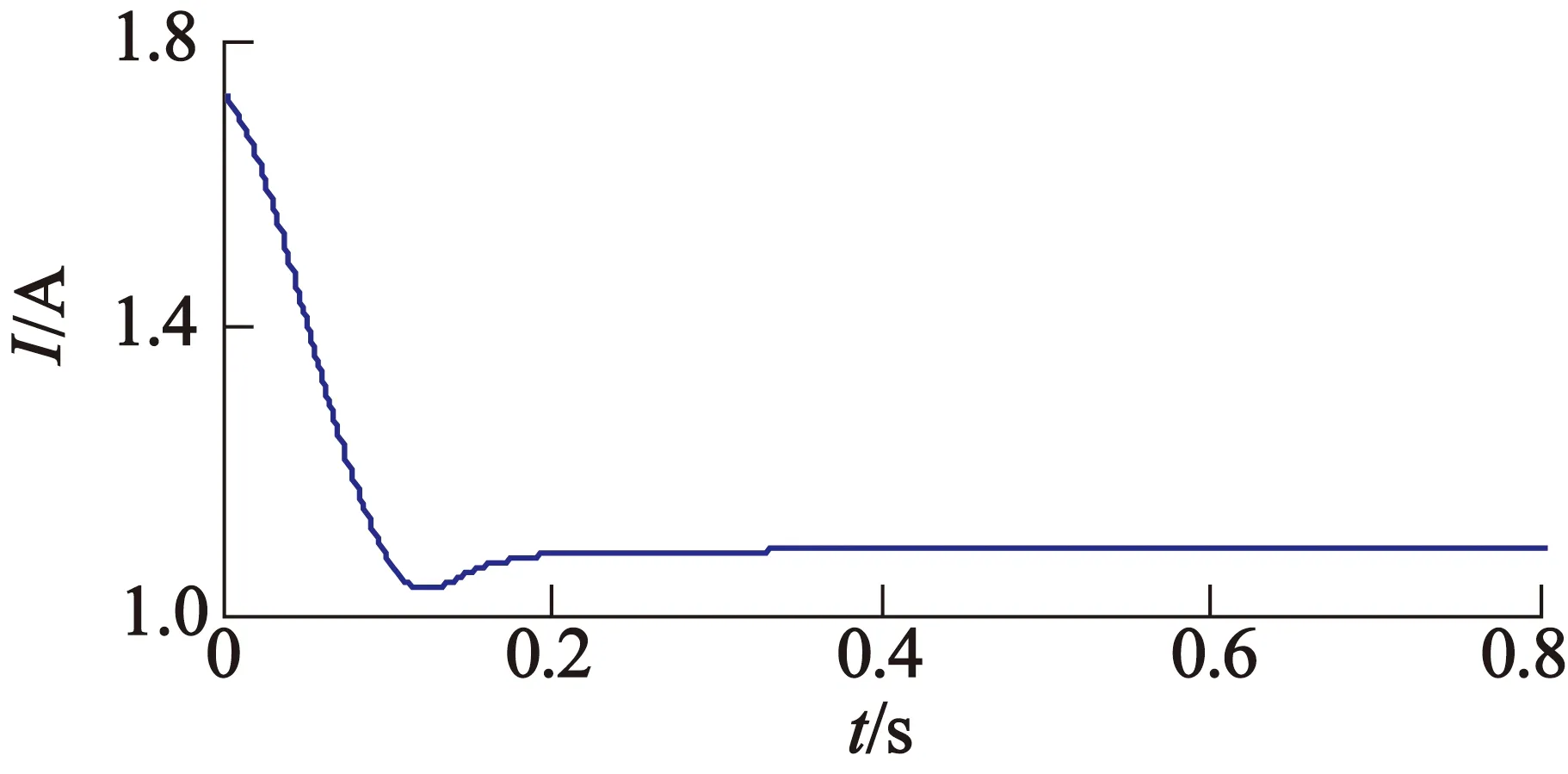
由圖9可知，PF1與PF2和PF2與PF3關系極弱，認為不相關；而PF3與PF4直到PF6與PF7中度相關；而PF7與PF8關系也極弱；PF8與PF9、PF9與PF10和PF10與PF11也中度相關。通常噪聲信號、換向電流和直流成分的頻率依次降低，而且LMD分離出PF分量也按頻率從高到低的順序排列。由于隨機噪聲之間以及隨機噪聲和換向電流之間的相關性較弱，所以可將PF1和PF2看作噪聲分量。換向電流之間的相關性較大，換向電流與直流分量是弱相關，所以PF3至PF7可認為是換向電流成分；剩余的是直流成分。按此方法獲得濾噪后的起動電流、換向電流和直流成分如圖10所示。

對比圖7和圖10及其局部放大圖可知，根據本文所提方法，LMD在起動階段和穩態運行時均可濾除啟動電流中的噪聲成分，獲取濾噪后的起動電流、換向電流和直流分量。

根據式(17)可得基于LMD的換向電流能量譜，如圖11所示。圖11中起動階段換向電流能量較大，穩態運行時能量較小，與直流電機常識相符合。穩態運行時，換向電流頻率在1 128Hz附近波動，波動的原因主要因為直流電機很難做到直線換向，存在提前或延遲換向現象。根據文獻[8]中轉速與頻率的關系，可知穩態轉速為1 538r/min；閃光測速儀測的穩態轉速為1 535r/min。以上試驗結果驗證了運用LMD分析換向電流的可行性和有效性。

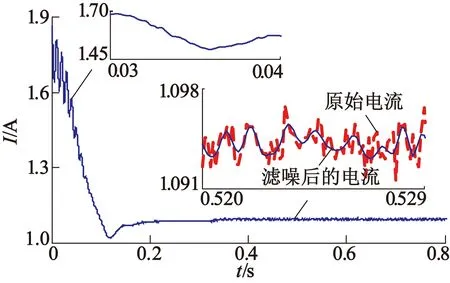
(a) 濾噪后的電流

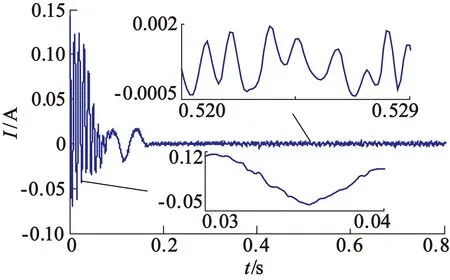
(b) 提取的換向電流

(c) 提取的直流分量

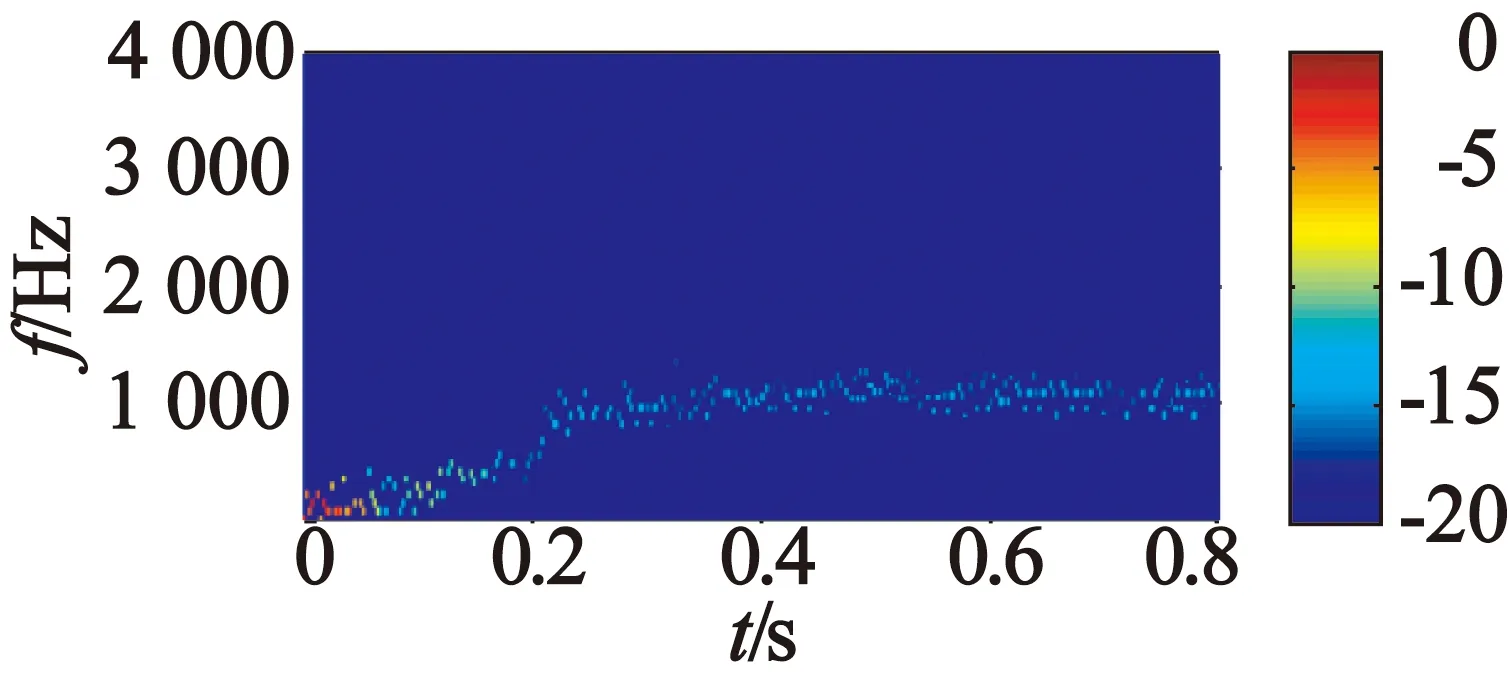
圖11 基于LMD的換向電流能量譜

4 結 語

本文通過運用LMD分析了直流電機空載起動過程中的電樞電流，主要結論如下：

1) 仿真信號分析結果表明，較之HHT，LMD求取的瞬時幅值和瞬時頻率在端點處的效果較好，不存在邊際飛翼現象；基于LMD的換向電流能量譜聚集性較好，端點處無發散現象。

2) 通過LMD不僅可有效濾除電樞電流中的高頻噪聲，還可提取電樞電流中高頻的換向電流和直流電流；

3) 基于LMD的換向電流能量譜可顯示換向電流的能量-時間-頻率之間的三維關系，為分析換向電流的瞬時幅頻特性提供了一種新的方法。

[1] 湯蘊璆，徐德淦．電機學[M]．北京：機械工業出版社，2012．

[2] 安宗裕，汪泉弟，彭河蒙．汽車雨刮電機電磁干擾特征提取方法[J].電機與控制學報，2012，16(7)：1-6．

[3] 崔淑梅，陳釗，宋立偉．直流電機換向有限元仿真模型的研究[J]．微電機，2011，44(2)：1-5．

[4] 李宗陽，吳旭升，張俊洪，等．異槽式單疊繞組直流電機換向性能研究[J]．電機控制學報，2008，12(5)：277-280，287．

[5] 石山，勵慶孚．直流電機換向火花的數值分析[J]．電工電能新技術，2001，20(4)：42-45，60．

[6] 黃傳金，宋海軍，陳鐵軍，等．基于EMD濾波的直流電動機起動電流高頻分量提取方法[J]．微特電機，2013，41(5)：28-31．

[7] 黃傳金，宋海軍，陳鐵軍，等．微型直流電動機電樞電流提取新方法[J]．微特電機，2013，41(4)：10-13．

[8] 牛發亮，黃進．漸進信號瞬時頻率提取及其在電機性能測試中的應用[J]．電工技術學報，2006，21(4)：122-126．

[9] 袁寶國，周政新，胡志華．直流電動機無傳感器測速實驗方法[J]．微特電機，2007，35(11)：20-22．

[10] 史敬灼，果寧，劉寶廷，等．單相交流串勵電機無傳感器轉速測量方法[J]．微特電機，2002，30(6)：17-19．

[11] 黃傳金，曹文思，陳鐵軍，等．局部均值分解在電力系統間諧波和諧波失真信號檢測中的應用[J]．電力自動化設備，2013，33(9)：68-73．

[12] 宋海軍，黃傳金，劉宏超，等．基于改進 LMD 的電能質量擾動檢測新方法[J]．中國電機工程學報，2014，34(10)：1700-1708．

[13] 黃傳金，鄔向偉，曹文思，等．基于LMD的全矢包絡技術及其TRT振動故障診斷中的應用[J]．電力自動化設備，2015，35(2)：168-174．

[14] 程軍圣，楊怡，張亢，等．基于局部均值分解的循環頻率和能量譜在齒輪故障診斷中的應用[J]．振動工程學報，2011，24(1)：78-83．

[15] HUANG N E，SHEN Z，LONG S R，et al．The Empirical mode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis[J]．Proc.R.Soc.Lond．A， 1998，454：903-995．

[16] RILLING G,FLANDRIN P.On empirical mode decomposition and its algorithms[C]//IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing,NSIP2003,Grado,Italy.2003：327-331. ----------------------

Study on LMD-Based DC Motor Commutation Current Analysis

JIShao-long1,JIBao-jie1,LIGuan-wen2,LIJian-feng3

(1.Henan Agricultural University,Zhengzhou 450002,China;2.96520 Troop of PLA,Luoyang 471000,China;3.Air Defense Forces Academy of PLA,Zhengzhou 450052,China)

A new method of analyzing DC motor commutation current was presented based on LMD. Firstly, the shortcomings of the armature current signal DC motor no-load starting was decomposed into a series of product function by LMD. Secondly, the concept of correlation coefficient of adjacent PF was defined and the PF order of the component of the commutation current and the DC component was determined according to the correlation coefficient. Finally, the energy spectrum of commutation current based on LMD was obtained. Simulation and experimental results demonstrate the correctness of the method proposed in this paper.

commutation current; local mean decomposition (LMD); product function (PF)； correlation coefficient; energy spectrum

2015-09-08

河南省科技廳科技攻關項目(142102210158)

TM33

A

1004-7018(2016)05-0021-05

姬少龍(1963-)，男，實驗師，從事電機測試方面的研究工作。