趨近律參數(shù)優(yōu)化的永磁同步電動(dòng)機(jī)模糊滑模控制
姚江云,吳方圓 ,覃 溪
(1.廣西科技大學(xué) 鹿山學(xué)院,柳州 545616;2廣西科學(xué)技術(shù)情報(bào)研究所,南寧 530022)
趨近律參數(shù)優(yōu)化的永磁同步電動(dòng)機(jī)模糊滑模控制
姚江云1,吳方圓2,覃 溪1
(1.廣西科技大學(xué) 鹿山學(xué)院,柳州 545616;2廣西科學(xué)技術(shù)情報(bào)研究所,南寧 530022)
研究了一種趨近律參數(shù)優(yōu)化的模糊滑模控制方法,應(yīng)用到永磁同步電動(dòng)機(jī)轉(zhuǎn)速控制中。采用神經(jīng)網(wǎng)絡(luò)優(yōu)化趨近律參數(shù),提取趨近律參數(shù)的最優(yōu)曲線,在此基礎(chǔ)上設(shè)計(jì)了滑模變結(jié)構(gòu)控制器實(shí)時(shí)修正趨近律參數(shù),最后應(yīng)用到PMSM轉(zhuǎn)速控制中。仿真及實(shí)驗(yàn)結(jié)果表明,該方法具有良好的靜態(tài)、動(dòng)態(tài)特性和魯棒性。
永磁同步電動(dòng)機(jī);趨近律參數(shù)優(yōu)化;滑模控制;轉(zhuǎn)速控制
0 引 言
永磁同步電動(dòng)機(jī)(以下簡(jiǎn)稱PMSM)是一個(gè)非線性強(qiáng)耦合的系統(tǒng),若采用常規(guī)的PID 控制,很難得到滿意的控制效果。文獻(xiàn)[1-2]采用了傳統(tǒng)滑模控制進(jìn)行了轉(zhuǎn)速環(huán)的設(shè)計(jì),文獻(xiàn)[3]設(shè)計(jì)了一種基于新型趨近率的PMSM滑模控制策略,都取得較為良好的效果。但都沒(méi)有對(duì)趨近律的不確定參數(shù)進(jìn)行處理,都是取最大值最小值或粗劣估算,使得控制器參數(shù)不能針對(duì)控制對(duì)象模型的變化而變化。
本文設(shè)計(jì)了一種趨近律參數(shù)優(yōu)化的滑模變結(jié)構(gòu)控制方法。具體方案為首先搭建傳統(tǒng)的PMSM滑模控制模型,使其在全速、重載、空載、干擾等各種工況下運(yùn)行,然后提取數(shù)據(jù)并導(dǎo)入設(shè)計(jì)好的RBF神經(jīng)網(wǎng)絡(luò)模型中進(jìn)行訓(xùn)練,提取趨近律參數(shù)最合適的變化范圍,用來(lái)設(shè)計(jì)滑模滑模變結(jié)構(gòu)控制器,最后將此方法應(yīng)用到PMSM的調(diào)速控制中,有利于控制性能的進(jìn)一步提高。
1 PMSM建模
建立永磁同步電動(dòng)機(jī)d,q軸轉(zhuǎn)速數(shù)學(xué)模型,當(dāng)id=0時(shí),如下式:
(1)
d,q軸電流數(shù)學(xué)模型如下:
(2)
式中:Ld,Lq為d,q軸定子電感;p為極對(duì)數(shù);id,iq為d,q軸定子電流;ud,uq為d,q軸定子電壓;R為定子繞組;ψf為轉(zhuǎn)子磁通;ωr為轉(zhuǎn)子角速度;B為阻力摩擦系數(shù);J為轉(zhuǎn)動(dòng)慣量。
2 整體控制方案設(shè)計(jì)
能夠使滑模控制器以何種規(guī)律趨近并沿滑模面不斷變化的重要因素就是趨近律,一般在滑模變結(jié)構(gòu)控制中都使用指數(shù)趨近律設(shè)計(jì)滑模控制器,即:
(3)
式中:ε,k為不確定參數(shù),k具有改進(jìn)系統(tǒng)的動(dòng)態(tài)特性的作用,能夠改變系統(tǒng)向滑模面的趨近速率,ε具有消除攝動(dòng)及外干擾的作用。根據(jù)文獻(xiàn)[4-5]所設(shè)計(jì)的滑模控制器模型可知,在實(shí)際應(yīng)用時(shí),對(duì)于趨近律中的ε,k均作保守估計(jì),取一個(gè)很大的值或取一個(gè)很小的值,這樣會(huì)使系統(tǒng)穿越滑模面時(shí)速度很大而導(dǎo)致抖動(dòng)增強(qiáng),或者速度很慢導(dǎo)致系統(tǒng)實(shí)時(shí)性差。因此,本文決定首先根據(jù)實(shí)際控制對(duì)象,尋找ε,k的最佳取值范圍,然后以此范圍為限制,設(shè)計(jì)滑模控制器,最后通過(guò)不斷采集PMSM的相關(guān)參數(shù),通過(guò)模糊控制計(jì)算出最合適的ε,k參數(shù)值,對(duì)ε,k在規(guī)定的范圍內(nèi)進(jìn)行實(shí)時(shí)修改,使得整個(gè)滑模控制器以最快的速度平穩(wěn)準(zhǔn)確地到達(dá)滑模面,相比于直接取最大值的方法能夠減小抖動(dòng),改善控制性能。圖1為整體結(jié)構(gòu)框圖。
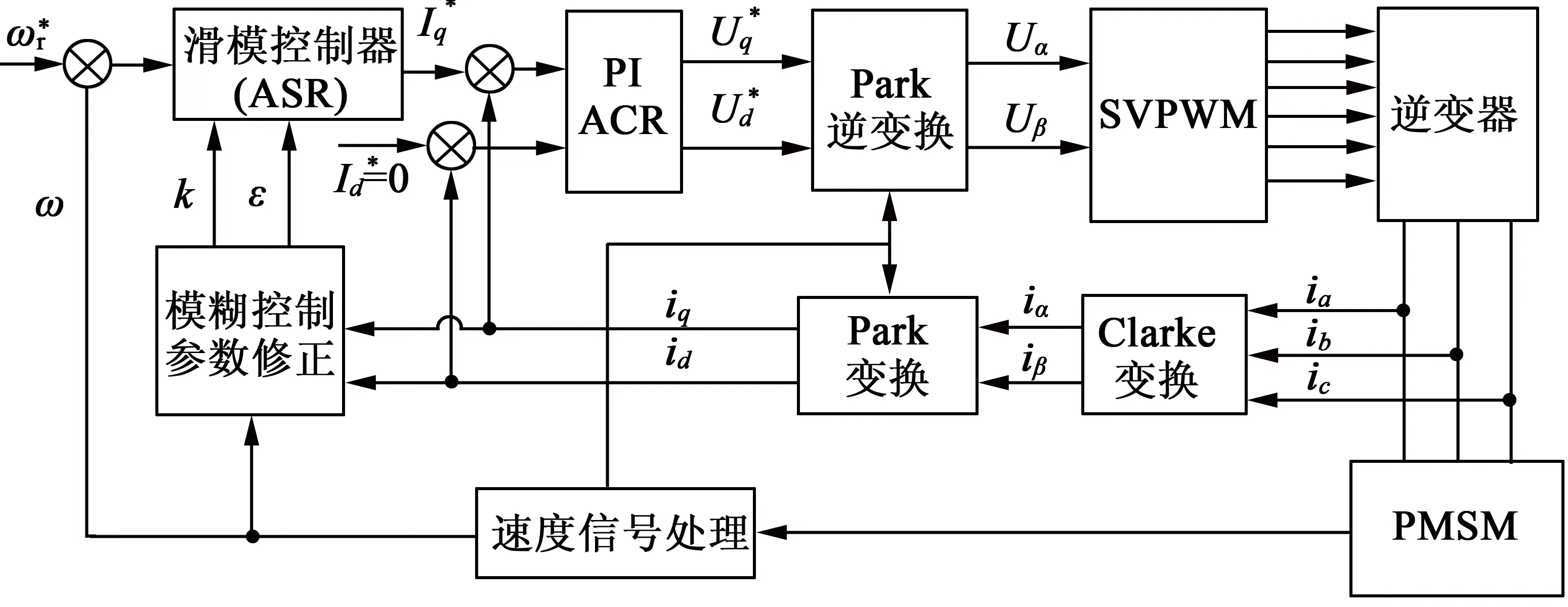
圖1 整體控制結(jié)構(gòu)框圖
3 趨近律參數(shù)的優(yōu)化
設(shè)計(jì)中采用RBF神經(jīng)網(wǎng)絡(luò)作為參數(shù)優(yōu)化器[6-7]。首先在Simulink中搭建基于傳統(tǒng)滑模變結(jié)構(gòu)控制的PMSM控制模型,然后分別在全速范圍內(nèi)重載、空載、擾動(dòng)情況下運(yùn)行,并采集此時(shí)的d,q軸的電流id,iq,電機(jī)的轉(zhuǎn)速ω作為RBF神經(jīng)網(wǎng)絡(luò)的輸入量,在滑模控制器趨近律不確定參數(shù)ε,k的最大取值范圍內(nèi)將其離散化,將離散化后的數(shù)據(jù)作為RBF神經(jīng)網(wǎng)輸出量對(duì)其進(jìn)行訓(xùn)練,最后選取ε,k輸出數(shù)據(jù)最為集中且平滑的曲線作為最終的ε,k參數(shù)變化范圍,此時(shí)ε,k的取值范圍遠(yuǎn)遠(yuǎn)小于原始的取值范圍,進(jìn)而能夠保證控制精度及系統(tǒng)的平穩(wěn)性。RBF神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)采用3-5-2結(jié)構(gòu),圖2為本文經(jīng)過(guò)多次訓(xùn)練后,得到的ε,k的最優(yōu)取值范圍曲線。
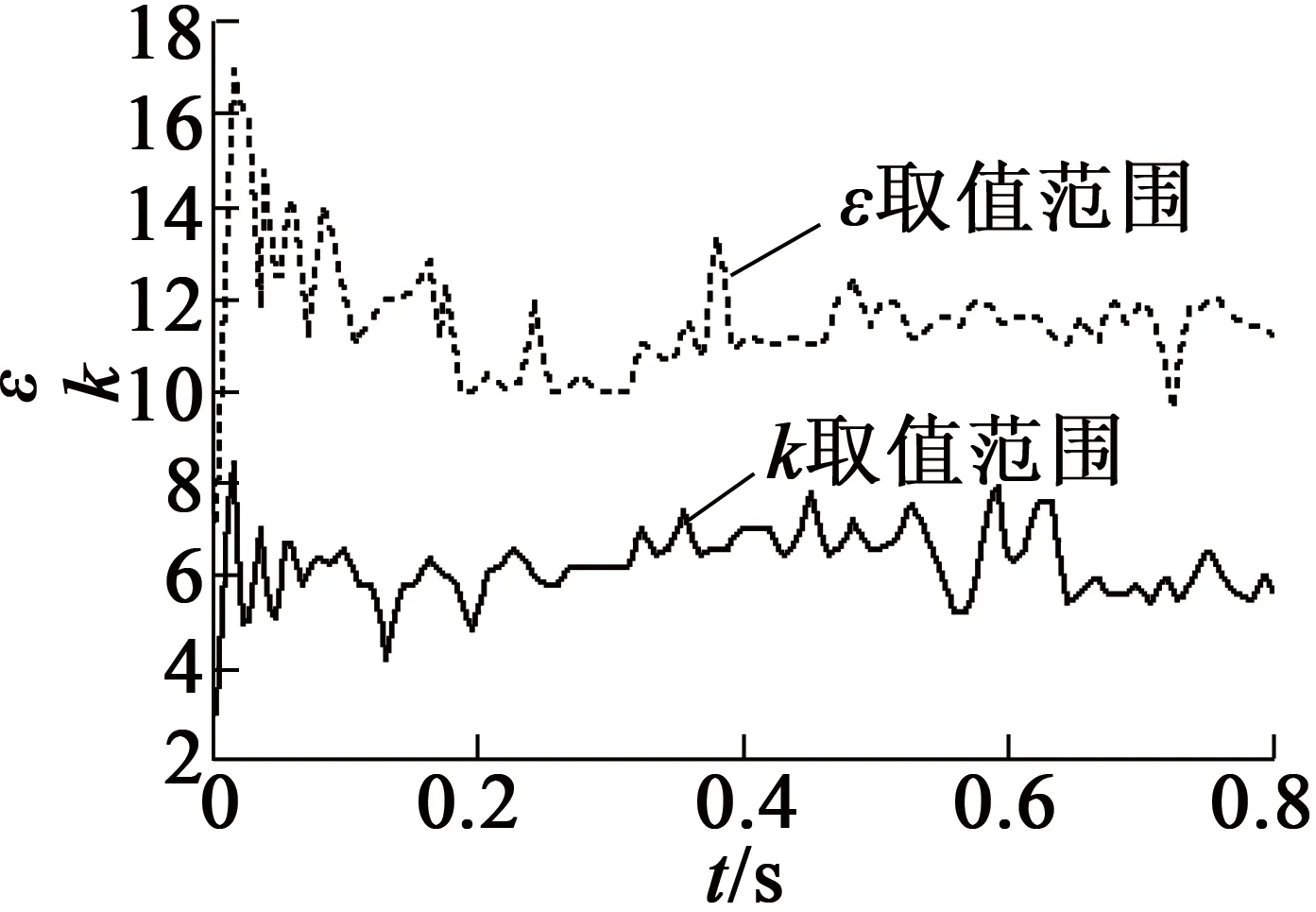
圖2 趨近律參數(shù)優(yōu)化取值范圍
在傳統(tǒng)的滑模控制中,一般k為(0,10),ε為(0,20)。由圖可知,在全工況情況下,經(jīng)過(guò)優(yōu)化后k的取值范圍為(3,8.5),ε的取值范圍為(7,17),相比于傳統(tǒng)的經(jīng)驗(yàn)法取值法,取值范圍減小了,這樣可以避免在控制過(guò)程中出現(xiàn)的劇烈抖動(dòng),進(jìn)而提高系統(tǒng)的控制精度和穩(wěn)定性。
4 趨近律參數(shù)優(yōu)化后的PMSM模糊滑模轉(zhuǎn)速控制
4.1 轉(zhuǎn)速滑模控制器的設(shè)計(jì)
(1)滑模面的設(shè)計(jì)
狀態(tài)變量:
(4)
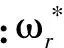
(5)
滑模面選用積分滑模面如下:
(6)
代入狀態(tài)變量得:
(7)
(2)速度控制量的輸出
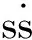
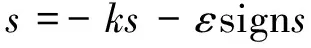
(8)
式中:ε=(7,17),k=(3,8.5)。
對(duì)滑模面求導(dǎo)得:
(9)
聯(lián)立狀態(tài)方程和滑模面可得:
(10)
4.2 基于模糊控制的參數(shù)修正
為了使趨近律參數(shù)的每一次取值都盡量接近控制目標(biāo),本文通過(guò)不斷采集系統(tǒng)運(yùn)行過(guò)程中的相關(guān)參數(shù),采用模糊控制設(shè)計(jì)了趨近律參數(shù)修正控制器。由式(10)可知,ε,k的取值與iq,轉(zhuǎn)速ω具有一定的解析關(guān)系,因此可以根據(jù)此關(guān)系設(shè)計(jì)控制ε,k變化的模糊控制器來(lái)根據(jù)系統(tǒng)運(yùn)行情況不斷修正參數(shù)。分別將iq,ω,ε,k的具體取值范圍轉(zhuǎn)換到規(guī)范論域,并對(duì)應(yīng)到設(shè)置的語(yǔ)言變量,iq,ω為[SMB],ε,k為[VSSMBVB]中,選取高斯隸屬函數(shù),模糊控制規(guī)則一般是根據(jù)經(jīng)驗(yàn)及推理后設(shè)定的,規(guī)則如表1所示。
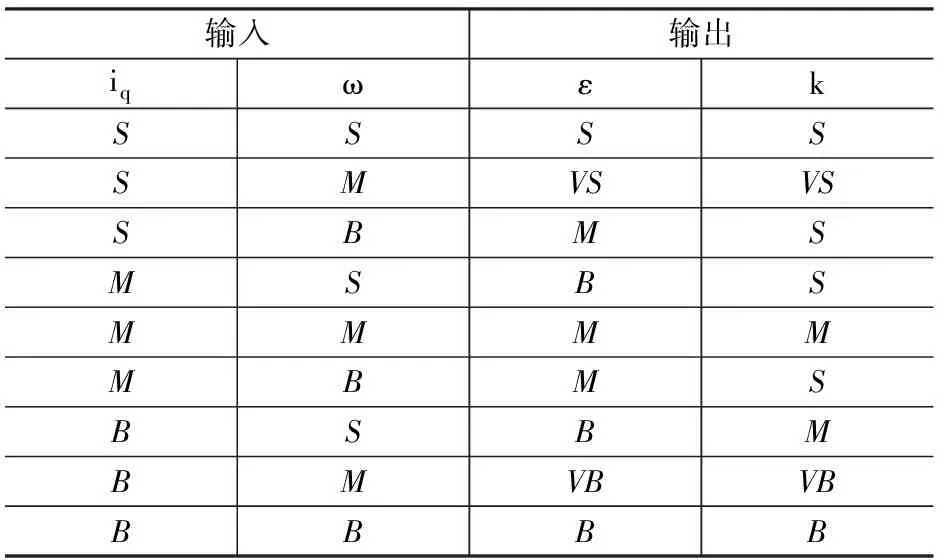
表1 模糊規(guī)則推理表
5 控制系統(tǒng)的仿真及實(shí)驗(yàn)驗(yàn)證
為了初步驗(yàn)證本算法的有效性,只在速度環(huán)上應(yīng)用本算法,而電流環(huán)仍然采用傳統(tǒng)PI控制。首先在Simulink環(huán)境下建立仿真模型進(jìn)行仿真,然后以DSPTMS320F2812為主控制器,搭建硬件平臺(tái),進(jìn)行控制算法的實(shí)驗(yàn)驗(yàn)證。控制系統(tǒng)整體建立步驟流程如圖3所示。
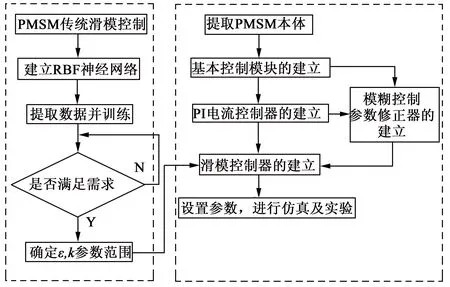
圖3 控制系統(tǒng)工作流程
仿真及實(shí)驗(yàn)系統(tǒng)中選取的電機(jī)參數(shù):額定功率PN=1kW,額定轉(zhuǎn)速ωr=2 500r/min,定子電阻R=0.95Ω,永磁體磁鏈ψf=0.245 2Wb,定子d,q軸電感Ld=3.5mH,Lq=15mH,定子轉(zhuǎn)動(dòng)慣量J=0.002kg·m2,電機(jī)極對(duì)數(shù)p=4。圖4為搭建的硬件實(shí)驗(yàn)系統(tǒng)。

圖4 硬件實(shí)驗(yàn)系統(tǒng)
圖5為傳統(tǒng)滑模變結(jié)構(gòu)控制與趨近律參數(shù)優(yōu)化后的模糊滑模變結(jié)構(gòu)控制下PMSM轉(zhuǎn)速響應(yīng)曲線。由圖5(a)可知,傳統(tǒng)的滑模變結(jié)構(gòu)控制超調(diào)量大,且系統(tǒng)的跟蹤性能較差,系統(tǒng)在0.2s時(shí)加入隨機(jī)擾動(dòng)之后抖動(dòng)較大。圖5(b)、圖5(c)為改進(jìn)后的控制算法的仿真及實(shí)驗(yàn)結(jié)果,可見(jiàn)改進(jìn)后的方法進(jìn)一步減少了系統(tǒng)超調(diào)量,且提高了控制精度,系統(tǒng)在加入隨機(jī)擾動(dòng)之后,系統(tǒng)抖動(dòng)較小,恢復(fù)穩(wěn)定速度較快。
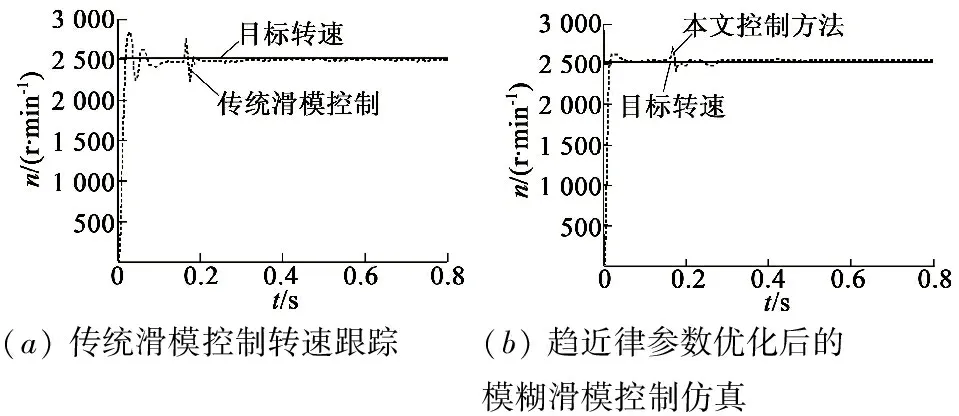
(a)傳統(tǒng)滑模控制轉(zhuǎn)速跟蹤(b)趨近律參數(shù)優(yōu)化后的模糊滑模控制仿真

(c) 趨近律參數(shù)優(yōu)化后的模糊滑模控制實(shí)驗(yàn)
圖5 轉(zhuǎn)速跟蹤曲線
圖6(a)為傳統(tǒng)滑模控制器的輸出。由于滑模控制器不能夠?qū)ν庠谀P蛥?shù)變化進(jìn)行實(shí)時(shí)預(yù)測(cè),使得控制器的輸出抖動(dòng)較大。圖6(b)、圖6(c)分別為改進(jìn)后的控制器輸出的仿真及實(shí)驗(yàn)結(jié)果。由于趨近律參數(shù)取值范圍集中,且在運(yùn)行過(guò)程中模糊滑模控制器能夠?qū)ζ溥M(jìn)行實(shí)時(shí)修正,使得控制器的輸出抖動(dòng)較小。
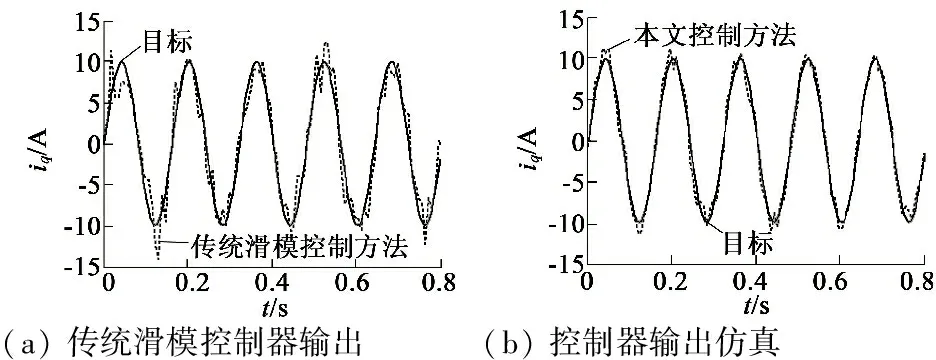
(a)傳統(tǒng)滑模控制器輸出(b)控制器輸出仿真
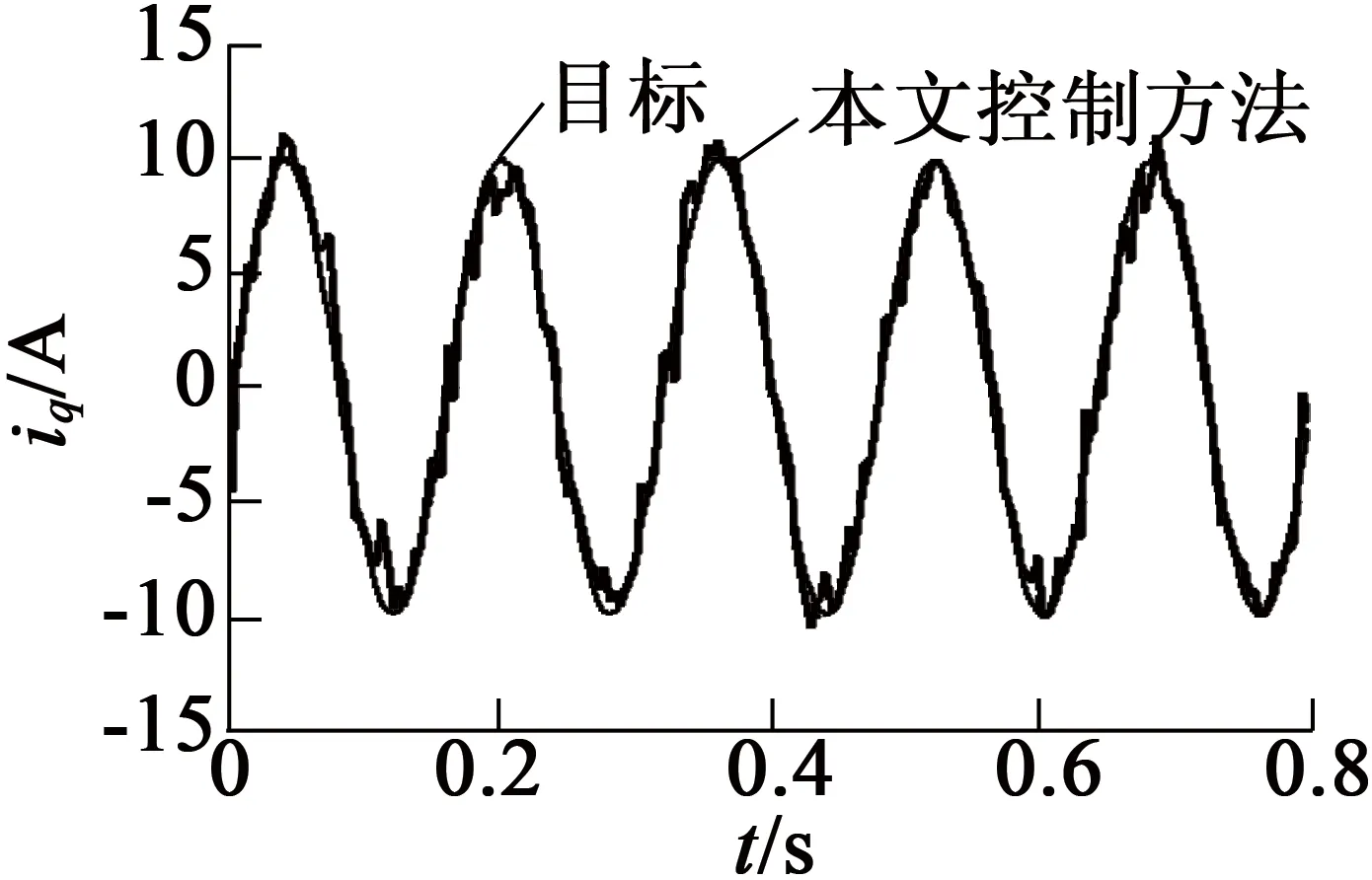
(c) 控制器輸出實(shí)驗(yàn)
圖6 控制器輸出曲線
圖7是給定負(fù)載下的轉(zhuǎn)速響應(yīng)曲線。在一定負(fù)載轉(zhuǎn)矩下給定轉(zhuǎn)速800 r/min,在0.15s時(shí)負(fù)載轉(zhuǎn)矩增加,比較轉(zhuǎn)速的變化情況;在0.35 s時(shí)給定轉(zhuǎn)速變?yōu)? 400 r/min,比較轉(zhuǎn)速的響應(yīng)情況。圖7(a)為傳統(tǒng)滑模控制下的轉(zhuǎn)速響應(yīng)曲線,系統(tǒng)起動(dòng)時(shí)抖動(dòng)較大,在一定轉(zhuǎn)速下,增加負(fù)載也會(huì)引起系統(tǒng)抖動(dòng),且在給定轉(zhuǎn)速上升時(shí),系統(tǒng)跟蹤過(guò)程中超調(diào)較大。圖7(b)、圖7(c)為改進(jìn)后的控制算法的轉(zhuǎn)速響應(yīng)曲線,系統(tǒng)起動(dòng)時(shí)抖動(dòng)較小,在一定轉(zhuǎn)速下,適當(dāng)增加負(fù)載,系統(tǒng)能夠快速恢復(fù)平穩(wěn),且在給定轉(zhuǎn)速上升時(shí),系統(tǒng)跟蹤過(guò)程中超調(diào)較小。

(a)傳統(tǒng)滑模控制(b)趨近律參數(shù)優(yōu)化后的模糊滑模控制仿真
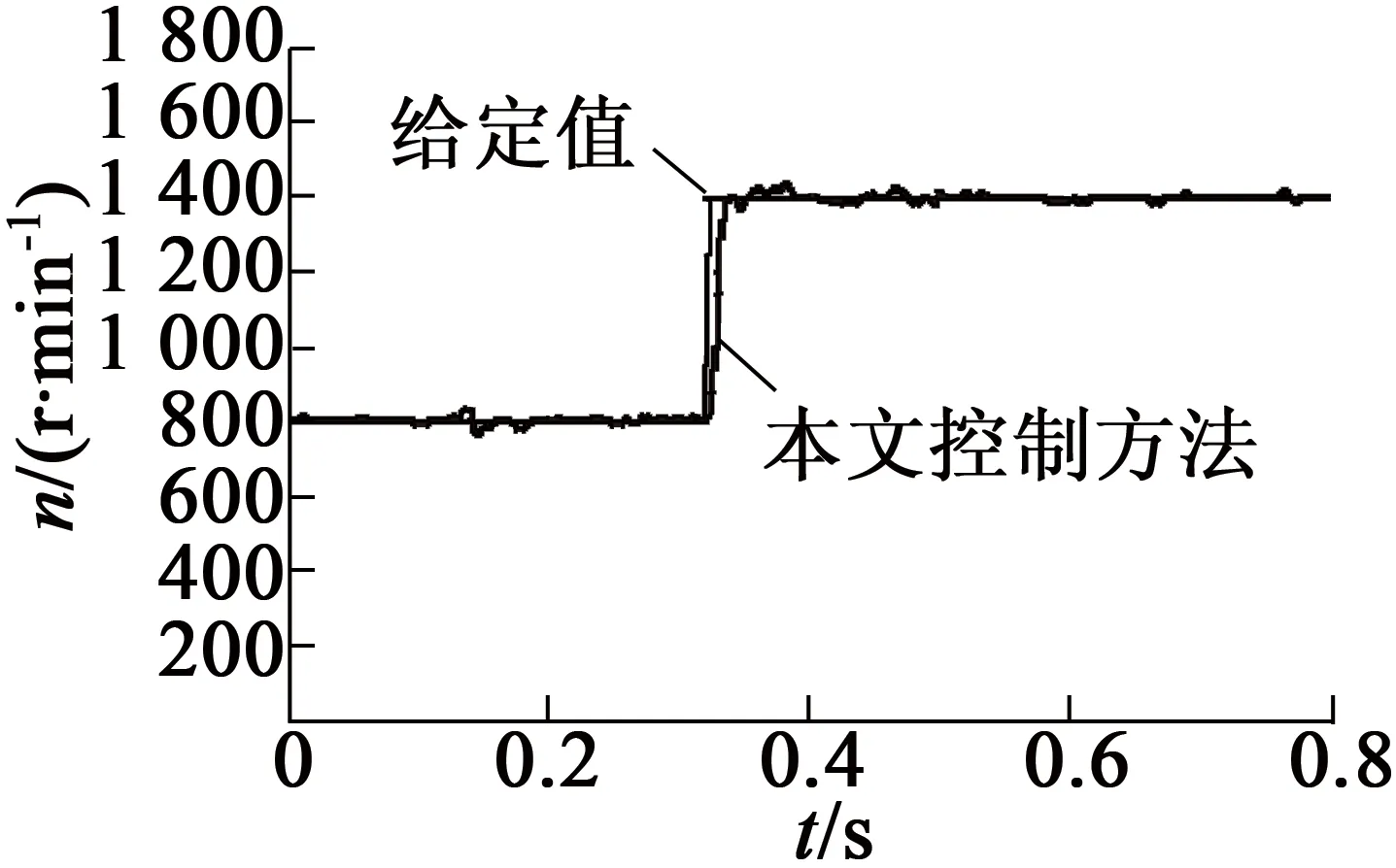
(c) 趨近律參數(shù)優(yōu)化后的模糊滑模控制實(shí)驗(yàn)
圖7 定負(fù)載下的轉(zhuǎn)速響應(yīng)曲線
6 結(jié) 語(yǔ)
本文設(shè)計(jì)了一種趨近律參數(shù)優(yōu)化的模糊滑模控制方法,并將其應(yīng)用到PMSM控制中取得良好的控制效果。本設(shè)計(jì)的不足之處是所研究的控制算法只在PMSM的轉(zhuǎn)速控制中較為有效,而對(duì)于位置控制是否同樣有效,還需要進(jìn)一步的實(shí)驗(yàn)研究。
[1] 賀宇軒,解小華,張愛(ài)春.基于滑模變結(jié)構(gòu)控制的永磁同步電機(jī)[J].吉林大學(xué)學(xué)報(bào)(信息科學(xué)版),2015,33(1):12-17.
[2] 張涌松,舒志兵.基于永磁同步電機(jī)的滑模變結(jié)構(gòu)仿真研究[J].機(jī)床與液壓,2008,36(7):288-292.
[3] 童克文,張興,張昱,等.基于新型趨近律的永磁同步電機(jī)滑模變結(jié)構(gòu)控制[J].中國(guó)電機(jī)工程學(xué)報(bào),2008,28(21):102-106.
[4] 王志宇,王長(zhǎng)松,范普成,等.基于滑模變結(jié)構(gòu)的永磁同步電機(jī)調(diào)速系統(tǒng)設(shè)計(jì)[J].微電機(jī),2011,44(6):52-56.
[5] 茅靖峰,吳愛(ài)華,吳國(guó)慶,等.永磁同步電機(jī)冪次變速趨近律積分滑模控制[J].電氣傳動(dòng),2014,44(6):50-53.
[6] 尹西杰,徐建國(guó).無(wú)刷直流電機(jī)的神經(jīng)滑模變結(jié)構(gòu)控[J].計(jì)算機(jī)仿真,2014,31(8):402-406.
[7] 李文波,王耀南.基于神經(jīng)網(wǎng)絡(luò)補(bǔ)償?shù)臋C(jī)器人滑模變結(jié)構(gòu)控制[J].計(jì)算機(jī)工程與應(yīng)用,2014,50(23):251-255.
Research on Fuzzy Sliding Mode Control of PMSM Based on Reaching Law Parameters Optimization
YAOJiang-yun1,WUFang-yuan2,QINXi1
(1.Lushan College of Guangxi University of Science and Technology,Liuzhou 545616,China;2.Institute of Science and Technology Information of Guangxi,Nanning 530022,China)
The fuzzy sliding mode variable structure control method based on reaching law parameters optimization was researched and applied to the speed control drive system in double closed loop of PMSM. First, the reaching law parameters was optimized by neural network, and extract the optimal parameters curve was extracted of reaching law.A fuzzy sliding mode controller based on the reaching law parameters optimization was designed, and applied to PMSM speed control system. The simulation results show that speed control system has good static, dynamic characteristics and anti-interference ability.
PMSM; reaching law parameters optimization; sliding mode control; speed control
2015-10-20
廣西科技大學(xué)鹿山學(xué)院自然科學(xué)基金項(xiàng)目(2013-LSZK08)
TM341;TM351
A
1004-7018(2016)05-0056-04
姚江云(1987-),女,碩士,講師,研究方向?yàn)殡姎庾詣?dòng)控制系統(tǒng)研究與設(shè)計(jì)。

