導數與單調性的同課異構對比分析

王剛陶++煜瑾

【摘要】三位省評優課一等獎獲得者的同課異構，各有千秋，說明了一節“好課”沒有固定的標準，沒有程式化的設計，但教師一定要肯下功夫，投入真感情，琢磨新套路，注重課堂的真實性、生成性和師生交流的和諧性.

【關鍵詞】真實性；生成性；和諧性；同課異構

教材對導數與函數單調性關系的解釋隱藏較深，不易提煉教學主線.因此，不同的教師對教材的編寫意圖有著不同的理解，不同的教學策略產生了不同的效果，這也使我對如何實現課堂的高效有了一個新的認識.以下是筆者對其中三位一等獎的授課情況的對比分析.1三位教師的教學過程簡介

1.1A教師的解釋過程

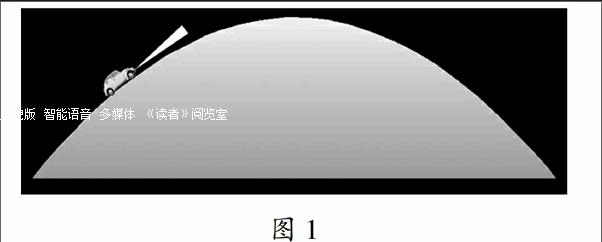
1.11問題情境：黑暗中，你是怎樣通過遠處汽車自身的燈光判斷該車是上坡還是下坡的？

A教師利用生活中的常見問題：“汽車燈光的指向與上下坡之間的聯系”，引導學生發現道路可以抽象成函數的圖象，燈光可以抽象為切線（圖1），這樣，問題就轉化為切線斜率與函數增減之間的聯系，從而輕松高效地聯系起導數與函數的單調性.

1.12猜想歸納：導數與函數的單調性有什么聯系呢？

從圖象上，我們發現，單調遞增區間上，曲線呈上升趨勢，函數單調遞增，每一點處的切線傾斜角均為銳角，斜率大于0（圖2）；在單調遞減區間上，曲線呈下降趨勢，函數單調遞減，每一點處的斜線傾斜角為鈍角，斜率小于0（圖3）.

于是，可以猜想結論：對于函數y=f（x），

如果在某區間上f′（x）>0，那么f（x）為該區間上的增函數；

如果在某區間上f′（x）<0，那么f（x）為該區間上的減函數.

A教師從“形”的角度，對具體例子進行動態演示，通過觀察、猜想到歸納、總結出結論，讓學生體驗知識的發現、發生過程.

1.13驗證猜想：請舉出幾個常見的函數，探究導數與函數單調性之間的聯系，驗證前面猜想的結論.

函數f（x）=x3+xf（x）=exf（x）=cosx，x∈0，π

圖象

單調性單調遞增單調遞增單調遞減

導數

符號f′（x）=3x2+1>0f′（x）=ex>0f′（x）=-sinx<0，

x∈（0，π）

A教師通過師生合作，歸納已經學過的常見函數的特征，進一步驗證了所猜想的結論的正確性.

1.14例題設置：

例1：確定函數f（x）=x2-4x+3在哪個區間上是增函數，在哪個區間上是減函數.

例2：確定函數f（x）=2x3-6x2+7在哪些區間上是增函數.

例3：確定函數f（x）=sinx（x∈（0，2π））的單調減區間.

變式：證明函數f（x）=sinx在區間（π2，3π2）上是單調減函數.

A教師從二次函數、三次函數到三角函數，讓學生體會導數法研究函數單調性的一般性和普遍適用性.

1.2B教師的解釋過程：

1.21認知沖突：是否能用已有的初等方法來確定函數f（x）=xlnx的單調區間？若不行，是否存在其它工具來研究該類函數的單調性.

B教師以學生的認知沖突為切入點，引導學生探究新方法，培養學生的好奇心，從而引入了導數工具，同時，讓學生感受導數法研究單調性具有一般性和有效性.

1.22數形結合：

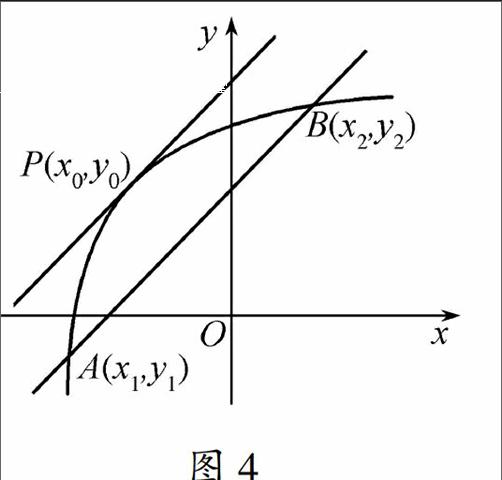
代數角度：函數y=f（x），在定義域內某區間I上，若對任意x1≠x2都有f（x1）-f（x2）x1-x2>0則函數在該區間上單調遞增，此時區間I為單調增區間.圖4

幾何角度：在區間I上，存在x=x0，使得fx1-fx2x2-x1=f′x0>0（圖4）.

故此，導數與函數單調性的關系為：

如果在某區間上f′（x）>0，那么f（x）為該區間上的增函數；

如果在某區間上f′（x）<0，那么f（x）為該區間上的減函數.

B教師采用中學生能夠接受的方式引入了拉格朗日中值來證明上述結論，用直觀的方法來分析和說明，培養學生嚴密的邏輯思維能力和意識.

1.23例題設置

證明函數f（x）=x3+x在R上單調遞增.

變式1：確定函數f（x）=x3-x在哪些區間上是增函數.

變式2：確定函數f（x）=ex-x的單調區間.

變式3：你能編制出相應一道題目嗎？

試結合y=x3思考：如果f（x）在某個區間上單調遞增，那么在該區間上必有f′（x）>0嗎？

B教師的例題設置從充分性與必要性兩個角度來讓學生理解導數與單調性的關系.

1.3C教師的解釋過程：

1.31尋找共性

函數的單調性刻畫了函數在某區間上的變化趨勢（上升或下降的變化趨勢）.

導數刻畫了函數在某點處的變化趨勢（圖像經過該點時的上升或下降趨勢）.

C教師基于學生的原有認知結構，從兩點知識的功能出發，尋找共性，引導學生猜測兩者之間可能存在的聯系.

1.32定義再探

單調遞增函數：函數y=f（x），在定義域內某區間I上，若對任意x1≠x2都有f（x1）-f（x2）x1-x2>0，則函數在該區間上單調遞增.

幾何解釋：區間I上任意兩點的割線斜率大于零則函數單調遞增.

導數的定義：當Δx→0時，ΔyΔx=fx0+Δx-fx0Δx→f′x0.

幾何解釋：當割線兩端點無限逼近時，割線斜率逼近切線斜率.

C教師引導學生從數學的本質“定義”出發尋找兩者之間的關系，通過兩個定義的再解釋，發現割線的斜率是溝通導數與單調性之間的紐帶.

1.33以直代曲

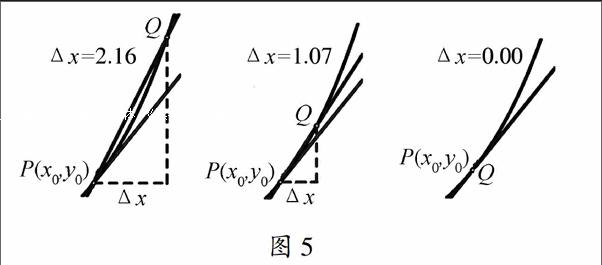
圖5

隨著點Q沿曲線向點P運動，割線PQ在P點附近越來越逼近曲線（圖5），當點Q無限逼近P點時，割線PQ最終成為在P點附近最逼近曲線的直線切線l（圖6）.圖6

C教師利用導數的本質思想：“以直代曲”溝通了導數與單調性之間的關系，即曲線經過P的上升與下降的變化趨勢可用P點處的切線斜率的正負來刻畫.

1.34量到質變

若f′x0>0刻畫的是曲線f（x）在點P0處的上升趨勢，那么若對任意x∈a，b都有f′（x）>0時，則函數f（x）在a，b上單調性如何呢？

C教師運用“動點成線”的原理，由曲線經過某區間內的每一點的上升與下降趨勢來刻畫函數在該區間內的單調性，從而由量變到質變獲得了結論.

1.35例題設置

例1：確定函數f（x）=x2-4x+3的單調區間.

例2：確定下列函數的單調區間.

（1）fx=2x3-6x2+7

（2）fx=xlnx

例3：請用導數證明f（x）=sinx-x在區間0，π上是減函數.

變式1：請思考該函數在區間-π，0、-π，π上的單調性？

變式2：請思考該函數在區間-π，π上導函數的符號？

變式3：結合以上問題判斷，函數單調遞減時，f′x<0一定成立嗎？

C教師的例題設置除了讓學生體會導數法研究函數單調性的一般性和普遍適用性以外，更利用例3的變式讓學生理解了導數法判斷函數單調性的非必要性.2教學目標的對比

教學目標是教學的航向，是教學成功與否的關鍵.三位教師的教學目標的主旨均為：理解導數與單調性的關系，掌握用導數法研究函數的單調性.通過課堂練習來看，三堂課學生基本都能掌握用導數法求解函數單調區間的步驟，然而在實現“理解導數與函數單調性的關系”這一目標時，三位教師所達到的效果不盡相同：A教師遵循的課堂展開思路是“猜想”——“驗證”——“實踐”，在這三個環節中結論是由不完全歸納得到，師生雖然花了大量的時間與例子去驗證，但在實踐過程中例題設置只是前者猜想歸納的簡單重復，沒有思維的層次性，學生沒能理解.B教師的例題設計有了層次性，并且設置了一個開放性問題，讓學生自主編寫題目，教師由此引導學生進一步思考：若函數單調遞增則f′（x）的符號是否一定為正？C教師的例題設置不僅完成了讓學生鞏固導數法求單調區間，并且每個例題都有其目的：例1的目的是讓學生感受導數法的有效性；例2的目的是讓學生感受導數法的一般性；例3及變式的安排是讓學生感受導數法證明函數單調性的工具性及非必要性.從目標的完成度來說C教師完成的更好，更自然.3重難點突破方法的對比

從教學過程中可看出三位教師確定的重難點均為：探索函數的單調性與導數的關系.但三位教師對這個內容的理解角度不同，處理方式也就不同：A教師的探索過程是由不完全歸納法得到，缺乏嚴密的推理論證，并且該教師是由從函數的單調性得出導數的正負，但在應用時又將該結論對調，邏輯較為混亂.B教師從學生能接受的角度引入了拉格朗日中值定理，學生能在一定程度上理解該定理，但由于缺乏羅爾中值定理的鋪墊，該定理的出現顯得很突兀.C教師能從學生的原有認知結構出發，緊扣教材，從導數的根本含義“以直代曲”的角度出發，由點到線，逐步深入取得了十分好的效果.從思維層次與教學效果來看，C教師的設計顯然更勝一籌.4總結

帶評比性質的公開課是教學“示范園”，它更多的是引導教師怎樣去做，它追求著這樣一個境界：教師在課堂上語言生動，具有感染力；教態灑脫，富有激情；教法精當，洋溢著布局之美.學生在教師的鼓動和引導下，充滿著生命的活力，課堂讓他們感受到學習的快樂.然而我們是否更應該追求課堂教學的本真：課堂思維的深度，師生的思維交流，學生的教育引導，教學設計的特色.都說課堂教學是一門遺憾的藝術，所以課堂教學更不應該追求表面的完美，應該留有“遺憾”.