把握方向 梳理方法 優(yōu)化方式
——“運(yùn)算定律和運(yùn)算性質(zhì)”復(fù)習(xí)課的教學(xué)實(shí)踐與反思
安徽太和縣第十一小學(xué)(236600)趙自為
?
把握方向梳理方法優(yōu)化方式
——“運(yùn)算定律和運(yùn)算性質(zhì)”復(fù)習(xí)課的教學(xué)實(shí)踐與反思
安徽太和縣第十一小學(xué)(236600)趙自為
[摘要]復(fù)習(xí)課在數(shù)學(xué)教學(xué)中的重要作用是顯而易見(jiàn)的,因?yàn)橛行У膹?fù)習(xí)可以加深學(xué)生對(duì)知識(shí)的記憶,避免遺忘。然而,在復(fù)習(xí)過(guò)程中,學(xué)生總會(huì)出現(xiàn)知識(shí)記憶不準(zhǔn)確、遺忘率高、應(yīng)用能力差等問(wèn)題,要想解決這些問(wèn)題,需要教師在復(fù)習(xí)教學(xué)中把握方向,梳理復(fù)習(xí)教學(xué)的方法,優(yōu)化教學(xué)方式,使學(xué)生真正理解和掌握所學(xué)的知識(shí)。
[關(guān)鍵詞]復(fù)習(xí)方法數(shù)學(xué)優(yōu)化運(yùn)算定律運(yùn)算性質(zhì)
德國(guó)心理學(xué)家艾濱浩斯揭示了遺忘發(fā)展的一條規(guī)律:“遺忘的進(jìn)程是不均衡的。在識(shí)記的最初遺忘得很快,以后逐漸減慢,到了相當(dāng)時(shí)間后,幾乎不再遺忘。”根據(jù)這條規(guī)律,教師必須搶在學(xué)生遺忘前及時(shí)進(jìn)行復(fù)習(xí),也就是平常所說(shuō)的趁熱打鐵。
在數(shù)學(xué)復(fù)習(xí)課教學(xué)過(guò)程中,我根據(jù)學(xué)生上課時(shí)出現(xiàn)的一些比較常見(jiàn)的問(wèn)題,及時(shí)進(jìn)行分析和歸納總結(jié),把零散的知識(shí)相互聯(lián)系起來(lái),使學(xué)生能夠進(jìn)一步明確數(shù)學(xué)學(xué)習(xí)中的知識(shí)點(diǎn),強(qiáng)化記憶并能靈活運(yùn)用。現(xiàn)結(jié)合教學(xué)實(shí)踐,談?wù)勛约涸诮虒W(xué)中總結(jié)的一些方法。
一、把握方向,明確復(fù)習(xí)目標(biāo)
眾所周知,復(fù)習(xí)課的主要特點(diǎn)就是對(duì)已經(jīng)學(xué)過(guò)的知識(shí)完成一個(gè)再現(xiàn)、整理、聯(lián)系并應(yīng)用的過(guò)程。這里需要強(qiáng)調(diào)的是,一個(gè)單元內(nèi)的知識(shí)點(diǎn)多且復(fù)雜,因此教師在復(fù)習(xí)講授之前,應(yīng)該認(rèn)真審視本單元需要復(fù)習(xí)的內(nèi)容,對(duì)其有一個(gè)整體的把握。這在很大程度上能夠幫助教師理清思路,明確教學(xué)目標(biāo)和導(dǎo)向,避免出現(xiàn)復(fù)習(xí)內(nèi)容遺漏等問(wèn)題。對(duì)于容易遺漏的復(fù)習(xí)內(nèi)容,教師應(yīng)該將其當(dāng)作重點(diǎn)內(nèi)容,引導(dǎo)學(xué)生反復(fù)記憶,避免遺忘。
例如,我在教學(xué)一節(jié)復(fù)習(xí)課時(shí),首先明確本單元的教學(xué)目標(biāo):(1)引導(dǎo)學(xué)生探索和理解加法、乘法運(yùn)算定律及減法與除法的性質(zhì),能運(yùn)用運(yùn)算定律和性質(zhì)進(jìn)行一些簡(jiǎn)單的計(jì)算;(2)培養(yǎng)學(xué)生根據(jù)具體情況選擇算法的意識(shí)與能力,發(fā)展其思維的靈活性;(3)使學(xué)生體驗(yàn)到知識(shí)的遷移性和方法的多樣性。只有在目標(biāo)明確之后,才能有針對(duì)性地進(jìn)行教學(xué)。然后我根據(jù)學(xué)生接受知識(shí)的能力,將學(xué)生分組,出示不同層次的復(fù)習(xí)題進(jìn)行訓(xùn)練,并進(jìn)行有針對(duì)性的講解。這樣教學(xué),既使不同層次的學(xué)生獲得發(fā)展,又提高了復(fù)習(xí)課教學(xué)的效率。
二、強(qiáng)化梳理,拓展復(fù)習(xí)方法
在明確一個(gè)單元的復(fù)習(xí)目標(biāo)之后,教師就可以制定相應(yīng)的教學(xué)計(jì)劃,參照教材的編排開(kāi)展復(fù)習(xí)活動(dòng)。對(duì)于復(fù)習(xí)課而言,知識(shí)的梳理無(wú)疑是核心環(huán)節(jié)。
例如,在“運(yùn)算定律和運(yùn)算性質(zhì)”教學(xué)中,鑒于知識(shí)點(diǎn)多且雜的特點(diǎn),我采用自主梳理和問(wèn)答式梳理相結(jié)合的方式,即將問(wèn)題留給學(xué)生,讓學(xué)生自己尋求解決問(wèn)題的方法,我只起引導(dǎo)和答疑的作用。這樣進(jìn)行復(fù)習(xí)教學(xué),有助于學(xué)生對(duì)知識(shí)的梳理,加深他們對(duì)知識(shí)點(diǎn)的記憶。課堂中,我先出示一道試題“1-2+3-4+5-6+7-8+9=?”,讓學(xué)生用自己喜歡的方法算一算。反饋交流時(shí),學(xué)生出現(xiàn)以下兩種方法。
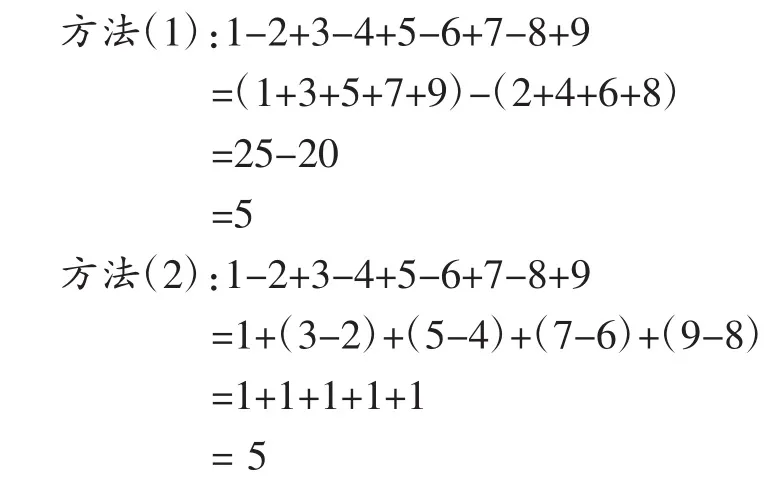
師:這一題運(yùn)用了什么運(yùn)算定律?
生:加法交換律。
接著,我將這一單元的運(yùn)算定律及性質(zhì)通過(guò)表格的方式呈現(xiàn)出來(lái),并讓學(xué)生說(shuō)說(shuō)自己是如何記憶這方面知識(shí)的,學(xué)生很快總結(jié)出了本節(jié)課知識(shí)梳理的方法——表格記憶法。用表格記憶法(見(jiàn)下表)進(jìn)行記憶,既有助于理清知識(shí)點(diǎn)的脈絡(luò),更清晰地展示復(fù)習(xí)課要復(fù)習(xí)的內(nèi)容,又能幫助學(xué)生明確知識(shí)的要點(diǎn)。這樣教學(xué),不僅凸顯復(fù)習(xí)課要復(fù)習(xí)的重點(diǎn)內(nèi)容,而且保證了課堂教學(xué)的有效進(jìn)行。同時(shí),我將復(fù)習(xí)重點(diǎn)放在知識(shí)的遷移和理解上,通過(guò)演練和拓展等方式,促使學(xué)生對(duì)知識(shí)的梳理更加深入。學(xué)生在明確了要復(fù)習(xí)的內(nèi)容后,能夠舉一反三地對(duì)知識(shí)進(jìn)行更深入的理解,從而靈活運(yùn)用所學(xué)知識(shí)解決問(wèn)題。

加法 乘法交換律:a+b=b+a 交換律:a×b=b×ac結(jié)合律:(a+b)+c=a+(b+c) 結(jié)合律:(a×b)×c=a×(b×c)分配律:(a+b)×c=a×c+b×c減法 除法性質(zhì):a-b-c=a-(b+c) 性質(zhì):a÷b÷c=a÷(b×c)
如果把梳理運(yùn)算定律和運(yùn)算性質(zhì)作為本節(jié)復(fù)習(xí)課的第一層次要求,將能靈活運(yùn)用運(yùn)算定律和性質(zhì)進(jìn)行簡(jiǎn)單的運(yùn)算看做是第二層次要求的話,那么更高層次的要求就是使學(xué)生能夠自覺(jué)地解決問(wèn)題,并進(jìn)行簡(jiǎn)單的運(yùn)算。我將這一部分的要求轉(zhuǎn)變?yōu)榧訌?qiáng)學(xué)生對(duì)數(shù)學(xué)運(yùn)算的整體感知和對(duì)數(shù)學(xué)算式的把握,這方面學(xué)生的表現(xiàn)都很突出,基本都能跟上我的思路進(jìn)行思考。但是,任何知識(shí)都需要不斷地重復(fù)記憶才能做到“伸手就來(lái)”“拿來(lái)就用”,所以教師在平時(shí)教學(xué)中要不斷地滲透之前學(xué)習(xí)過(guò)的內(nèi)容,使學(xué)生加深印象,在不知不覺(jué)中強(qiáng)化記憶。
三、優(yōu)化方式,提升復(fù)習(xí)效果
通過(guò)系統(tǒng)的知識(shí)梳理,學(xué)生已經(jīng)對(duì)學(xué)過(guò)的知識(shí)能有效提取了,這時(shí)教師需要組織足量、高質(zhì)的練習(xí)來(lái)幫助學(xué)生提升解題水平。復(fù)習(xí)課的訓(xùn)練主要體現(xiàn)在以下兩個(gè)方面:
1.關(guān)注變式,凸顯知識(shí)本質(zhì)
復(fù)習(xí)課中例題的選擇、習(xí)題的配備必須精心考慮,題目要有一定的綜合性和啟發(fā)性,具有一定的典型意義,其側(cè)重點(diǎn)應(yīng)更多傾向于熟能生巧、巧中生智。因此,教師應(yīng)選擇一題多解、一題多變的題來(lái)開(kāi)拓學(xué)生的思路,培養(yǎng)學(xué)生的數(shù)學(xué)洞察力。
課件出示:你來(lái)試一試。
65+42-35 105-39-61 3×125×8
3200÷25÷4 72×7+28×7 25×44
在學(xué)生進(jìn)行上述算式的解答時(shí),我特別強(qiáng)調(diào)25×44要用兩種方法解答,即25×(40+4)和25×4×11。
在學(xué)生完成上述算式后,我出示32×102和35×14兩道算式,其實(shí)就是告訴學(xué)生32×102用32×(100+2)來(lái)計(jì)算比較簡(jiǎn)單,而35×14既可以用35×(10+4)進(jìn)行簡(jiǎn)便計(jì)算,又可以用35×2×7來(lái)進(jìn)行簡(jiǎn)便計(jì)算。同時(shí),我還讓學(xué)生關(guān)注解決問(wèn)題時(shí)需要注意的事項(xiàng):(1)看,即看題的數(shù)據(jù)和運(yùn)算符號(hào)的特點(diǎn);(2)想,即想能不能更簡(jiǎn)便計(jì)算,用什么方法會(huì)更簡(jiǎn)便計(jì)算;(3)算,即認(rèn)真進(jìn)行計(jì)算;(4)查,即完成后仔細(xì)檢查。
2.關(guān)注遷移,提升解題能力
教學(xué)活動(dòng)中設(shè)計(jì)的各種練習(xí)題,是學(xué)生進(jìn)行知識(shí)鞏固、檢測(cè)學(xué)習(xí)效果的一種重要途徑。所以,教師要重視復(fù)習(xí)時(shí)練習(xí)題的設(shè)計(jì),在優(yōu)化設(shè)計(jì)的同時(shí)激發(fā)學(xué)生解決問(wèn)題的興趣,提高他們的應(yīng)用能力。同時(shí),教師要注意在練習(xí)過(guò)程中適當(dāng)?shù)剡M(jìn)行拓展和引導(dǎo),為學(xué)生的進(jìn)一步學(xué)習(xí)做好準(zhǔn)備。

師(指著68×99+68、17×23-23×7、23×9-23×4+23× 5):你們發(fā)現(xiàn)了什么?
生:都把相同的因數(shù)拿出來(lái),將不同的因數(shù)放在一起。
師(出示題目,如下):你會(huì)算嗎?
(1)39×9+6×39-39×4(2)67×25+67×48+27×67
……
整節(jié)課的教學(xué),學(xué)生學(xué)得認(rèn)真,教師教得輕松,真正體現(xiàn)了“學(xué)生是學(xué)習(xí)的主體,教師是數(shù)學(xué)學(xué)習(xí)的組織者與引導(dǎo)者”的新課程理念。
當(dāng)然,除把握方向、梳理方法和優(yōu)化方式外,復(fù)習(xí)課的教學(xué)策略還有很多。希望通過(guò)我的這節(jié)復(fù)習(xí)課,能夠幫助其他教師以“明目標(biāo)、展過(guò)程、提效果”的務(wù)實(shí)精神,扎根課堂,持久探索,努力創(chuàng)造單元復(fù)習(xí)課的高效課堂。
反思:
本節(jié)課是一節(jié)典型的數(shù)學(xué)復(fù)習(xí)課,既突出學(xué)生自主梳理的過(guò)程,又注重引導(dǎo)學(xué)生構(gòu)建知識(shí)網(wǎng)絡(luò)、梳理方法及優(yōu)化遷移。
1.以學(xué)定教,體現(xiàn)學(xué)生的主體地位
新課程要求“以學(xué)定教”,“教”服務(wù)于“學(xué)”,從而真正確立學(xué)生是學(xué)習(xí)主體的地位。在本節(jié)課教學(xué)中,我采用學(xué)生自己嘗試整理、課上匯報(bào)交流的形式,把數(shù)學(xué)運(yùn)算依據(jù)的五大定律、兩大性質(zhì)歸納整理出來(lái),使學(xué)生認(rèn)識(shí)到加法和乘法有五大定律,減法和除法有兩大性質(zhì)。通過(guò)整理匯報(bào),既提高了學(xué)生的辨析能力,使教學(xué)更有實(shí)用性和實(shí)效性,又保證了學(xué)生在課堂上有充分的時(shí)間參與學(xué)習(xí),并盡可能地讓學(xué)生積極開(kāi)動(dòng)腦筋,交流自己的解題方法,將學(xué)過(guò)的知識(shí)系統(tǒng)地整理出來(lái),有效地減少遺忘。
2.知識(shí)梳理,幫助學(xué)生構(gòu)建知識(shí)網(wǎng)絡(luò)
通過(guò)整理和復(fù)習(xí),幫助學(xué)生建構(gòu)知識(shí)網(wǎng)絡(luò)(表格記憶法)是復(fù)習(xí)課的一項(xiàng)重要任務(wù),因?yàn)閷W(xué)生課前自主收集整理了運(yùn)算定律和簡(jiǎn)便計(jì)算的有關(guān)知識(shí),所以在課堂上能較好地進(jìn)行匯報(bào)交流。學(xué)生把小學(xué)階段學(xué)習(xí)過(guò)的運(yùn)算定律和性質(zhì)進(jìn)行歸納整理,教師注重通過(guò)多種題型的對(duì)比,引導(dǎo)學(xué)生根據(jù)運(yùn)算特點(diǎn)和數(shù)據(jù)特點(diǎn),靈活選用合理、簡(jiǎn)便的計(jì)算方法。這樣教學(xué),既加深了學(xué)生對(duì)知識(shí)的理解和鞏固,又使學(xué)生的知識(shí)系統(tǒng)更加完善。
3.注重能力,培養(yǎng)學(xué)生靈活、合理應(yīng)用的能力
運(yùn)算定律的運(yùn)用具有一定的靈活性,對(duì)數(shù)學(xué)能力的要求較高,而且運(yùn)算定律的運(yùn)用為培養(yǎng)和發(fā)展學(xué)生思維的靈活性提供了極好的機(jī)會(huì)。教學(xué)時(shí),我注重既讓學(xué)生探究、嘗試,又讓學(xué)生交流、質(zhì)疑。相應(yīng)的,教師也要充分發(fā)揮自身的主導(dǎo)作用,在學(xué)生探究時(shí),因勢(shì)利導(dǎo),不失時(shí)機(jī)地給予適度啟發(fā);在學(xué)生交流時(shí),耐心傾聽(tīng),了解學(xué)生的真實(shí)想法,幫助學(xué)生講清自己的算法,讓其他學(xué)生也能明白。
總之,教師要上好復(fù)習(xí)課,必須明確復(fù)習(xí)課教學(xué)的目標(biāo),對(duì)知識(shí)的梳理方法進(jìn)行有效的引導(dǎo),從而優(yōu)化教學(xué),使學(xué)生理解和掌握更多的數(shù)學(xué)知識(shí)。
(責(zé)編杜華)
[中圖分類(lèi)號(hào)]G623.5
[文獻(xiàn)標(biāo)識(shí)碼]A
[文章編號(hào)]1007-9068(2016)14-033

