相干態在量子相空間中二維正態分布

李海英, 趙建英

(1. 內蒙古師范大學 數學系， 內蒙古 呼和浩特 010022;2. 內蒙古商貿職業學院 社科與基礎教學部, 內蒙古 呼和浩特 010070)

?

相干態在量子相空間中二維正態分布

李海英1,2, 趙建英2

(1. 內蒙古師范大學 數學系， 內蒙古 呼和浩特 010022;2. 內蒙古商貿職業學院 社科與基礎教學部, 內蒙古 呼和浩特 010070)

摘要：將數理統計中的正態分布與物理學中的量子力學不確定性有效結合，通過二維正態分布密度函數和有序算符內的積分技術，簡單有效地求得量子空間中粒子坐標|x〉，動量本征態|p〉及相干態|z〉在 Fock 表象中的表達式，并證明其完備性.結果表明：通過采用數理統計及正規乘積方法，求證結果準確，且大大簡化了求證過程.

關鍵詞：正態分布; 量子空間; 相干態; 分布密度; 正規乘積

德國物理學家海森堡通過矩陣、正則變換、算符等數學語言創建算符與矩陣的關系式，提出物質系統的光譜關系式、海森堡對易關系式、測不準關系式、海森堡的矩陣力學方程等,以及數學化的矩陣力學理論闡述微觀世界的本質.利用具有統計性質的幾率密度描述量子在空間中的運動情況，量子的粒子狀態則采用波函數描寫.通過宏觀的軌道參數方程無法判定量子某一時刻是出現在A點或是B點，只能通過波函數測算量子出現在空間中某一點的概率，微觀粒子無固定軌道運動.數學方法在科學技術中的應用已有很多報道[1].本文根據微觀粒子的不確定性(統計性質)與數學概率統計中概率密度函數的相似性，利用二維正態分布的概率密度函數研究粒子的運動狀態.

1一維正態分布

一維隨機變量X的密度函數為

(1)

式(1)中:μ,σ均為常數，若σ>0，則變量X服從常數μ,σ的正態分布.

2二維正態分布

如果二維隨機變量(X,Y)聯合分布函數為F(x,y)，當f(x,y)≥0時，對任意實數x,y都滿足

(2)

函數f(x,y)是二維連續型隨機變量(X,Y)的概率密度或分布密度，如果其概率密度滿足

(3)

則二維隨機變量(X,Y)的概率密度為

(4)

式(4)中:σ1,σ2,u1,u2,ρ均為已知參數，如果σ1>0,σ2>0，-1<ρ<1，則二維隨機變量(X,Y)服從參數σ1,σ2,u1,u2的二維正態分布.當x,y,u1,u2的物理意義確定后，同樣可采用量子力學中的算符代替.

3正規乘積

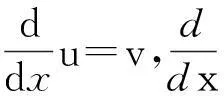
正規乘積的以上性質可簡化量子力學算符符號的積分運算，即正規乘積內的積分技術.

4坐標和動量表象

狄拉克最早把“表象”引入量子力學中，表象主要描述在不同坐標系下，體系的狀態和力學量的具體表示形式[3].他把系統狀態的波函數看成抽象空間中的態矢量在某個表象中的表示，力學量的本征函數即此空間的一組基矢，完備性是基矢成為表象的必要條件.

設Q,P分別為量子力學中坐標表象的坐標算符和動量表象的動量，Q,P本征態分別為|x〉和|p〉.由狄拉克符合表示方法，有

(5)

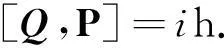
(6)

式(6)中:h為普朗克常數，引用Q,P的湮滅算符a和產生算符a+，a和a+滿足厄米共扼關系，一維諧振子的哈密頓量[4]為

(7)

由式(7)可知:a，a+滿足

(8)

根據式(8)，可得

(9)

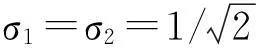
(10)

再根據正規乘積性質和∶exp(-a+a)∶=|0〉〈0|，有

(11)

令

(12)

則式(12)改寫為

(13)

同理可證

(14)

式(13)，(14)是坐標及動量本征態在Fock表象中的形式.在理論物理中，如果任意物理量A的算符A′作用在描述微觀體系狀態的某一狀態函數φ上，等于常數a乘以φ，即A′φ=aφ.則物理量A具有的確定數值a稱為物理量算符A′的本征值，φ稱為算符A′的本征態或本征函數. 由式(13)，(14)可知：f(x,p)=|x〉〈x||p〉〈p|，由量子力學中量子狀態的完備性,可得

(15)

5相干態表象

湮滅算符的本征態為|z〉相干態，復數z則為本征值[6-11].取σ1=1,σ2=1,ρ=0，則式(10)變為

(16)

根據正規乘積性質和∶exp(-a+a)∶=|0〉〈0|，聯合式(9)，(16)，有

(17)

(18)

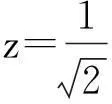
(19)

6結束語

在量子力學中闡述粒子狀態是建立在幾率的基礎上，通過數學中概率統計特性，將量子空間中的粒子狀態與概率統計有效地結合，利用概率統計中的連續型二維正態分布密度函數，推導出量子力學中的坐標表象、動量表象和相干態表象在Fock表象中的關系式.同時，簡捷地證明了其完備性.此方法不僅簡單、新穎、有效地簡化了推導過程，且很好地把數學方法應用于量子力學基本表象.

參考文獻：

[1]楊金勇.一類非線性比式和問題的分支定界算法[J].華僑大學學報(自然科學版),2015，35(3)：14-16.

[2]WICKG.Quantumphasespacetheorybasedonintermediatecoordinate-momentumrepresentation[J].PhysRev,1950，80：131-138.

[3]DIRACPAM.Theprinciplesofquantummechanics[J].PhysLettB,1930，72：38-41.

[4]DIRACPAM.量子力學原理[M].4 版.陳咸享，譯.北京:科學出版社,2010：61-89.

[5]范洪義.量子力學表象與變換論[M].上海:上海科學技術出版社,1997：97-181.

[6]曾謹言.量子力學(卷Ⅰ)[M].4 版.北京:科學出版社，2000：91-148.

[7]KLAUDERJR,SKARGERSTAMBS.Coherentstatesworldscientific[J].JSedimentRes,1985,23(7):67-69.

[8]范洪義.相干態在參數量子相空間的兩維正態分布[J].物理學報，2014,63(2):15-20.doi:10.7498/aps.63.020302.

[9]GLAUBERRJ.Thephilosophyofquantummechanics[J].PhysRev,1963,131(29):2766-2769.

[10]DIRAC P A M.Recollections of an exciting area, history of 20th century physics[M].New York:Academic Press,1977：59-102.

[11]CHEN Lin.Sources of quantum mechanics[J].Math J Phys,1966,23(7):781-785.

(責任編輯： 錢筠英文審校： 黃心中)

Two Variable Normal Distribution of Coherent States in Quantum Space

LI Haiying1.2, ZHAO Jianying2

(1. Mathematical School, Inner Mongolia Normal University, Hohhot 010022, China;2. Department of Social Sinence and Basic teaching, Inner Mongolia Business and Trade College， Hohhot 010070， China)

Abstract：Normal distribution in mathematical statistics and the uncertainty of quantum mechanics in physics are effectively combined, by two dimensional normal distribution density function and orderly operator of integral technology, simple quantum particle in the space coordinate |x〉, momentum intrinsic state |p〉 and coherent state |z〉expression in Fock representation are obtained effectively, and its completeness is also proved. By using mathematical statistics and normal product method, we show that the obtained result is not only accurate but also greatly simplifies the process of verification.

Keywords：normal distribution; puantum space; coherent state; density function; normal product

中圖分類號：O 211.3; O 413.1

文獻標志碼：A

基金項目：內蒙古自治區高等學校科學研究基金資助項目(NJZY16399)； 中國教育學會“十一五”科研規劃重點基金資助項目(ZY0084)

通信作者：李海英(1968-)，女，副教授，主要從事高等數學的研究.E-mail:sunjinpo838@163.com.

收稿日期：2016-03-03

doi:10.11830/ISSN.1000-5013.2016.03.0391

文章編號：1000-5013(2016)03-0391-04