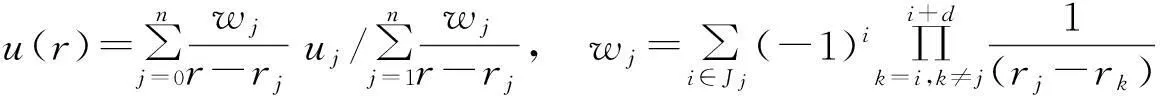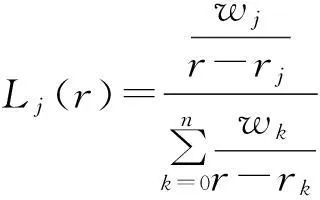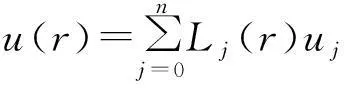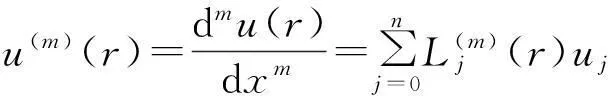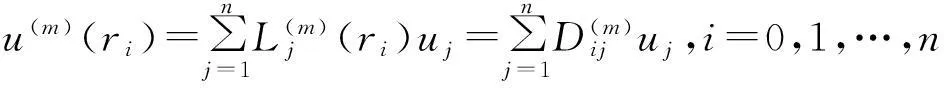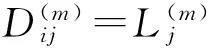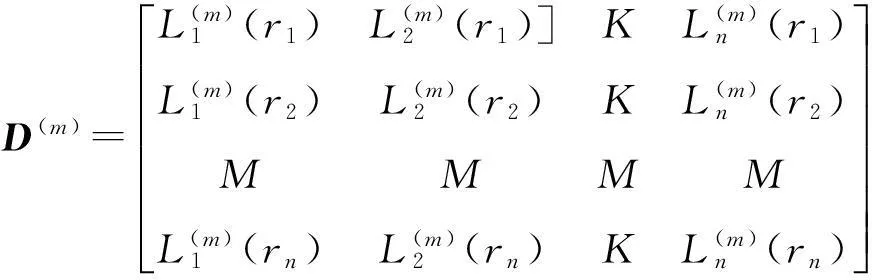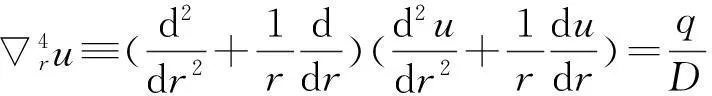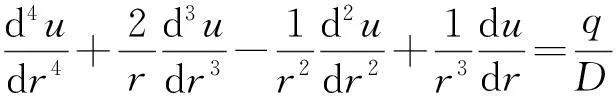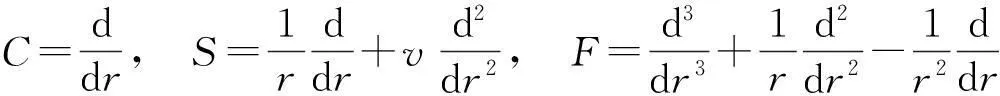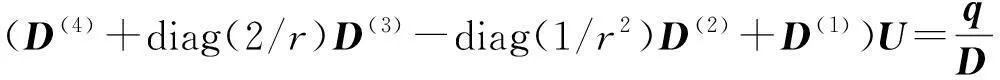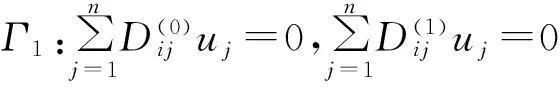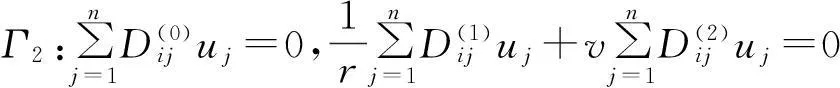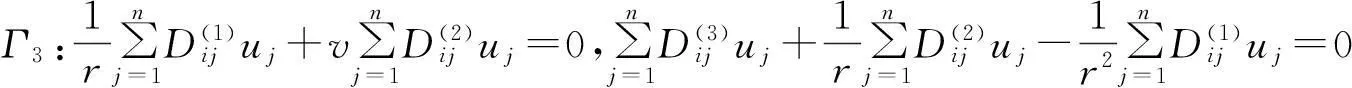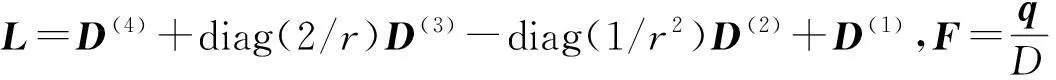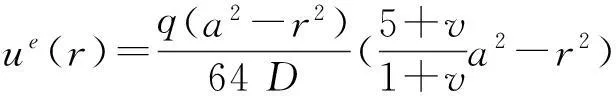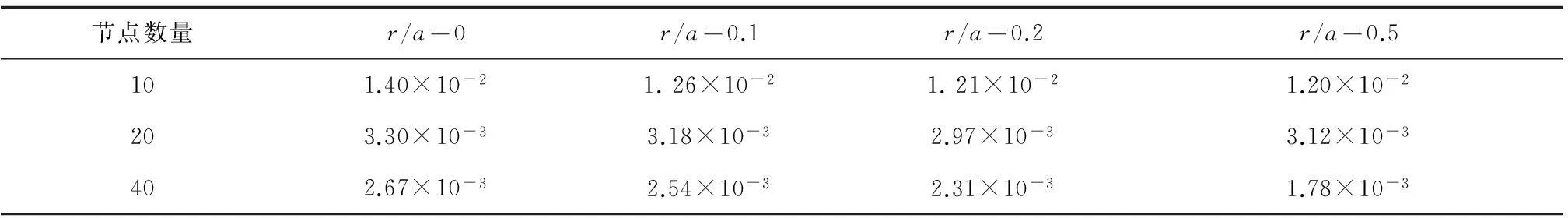極坐標下薄板彎曲問題的重心有理插值法

莊美玲，王兆清，張磊，紀思源

(山東建筑大學力學研究所，山東 濟南 250101)

?

極坐標下薄板彎曲問題的重心有理插值法

莊美玲，王兆清*，張磊，紀思源

(山東建筑大學力學研究所，山東 濟南 250101)

摘要：利用重心有理插值配點法(BRICM)研究了極坐標下薄板的彎曲問題，該方法是以重心有理插值近似未知函數強迫微分方程在離散節點處成立，得到微分方程的離散代數方程組，進而采用重心有理插值的微分矩陣將離散代數方程組表達為矩陣的形式。利用置換法施加邊界條件，求解微分方程組。數值算例結果表明，該方法在解決極坐標下薄板彎曲問題上公式簡單，程序實施方便且計算精度高。

關鍵詞：極坐標;彎曲問題；重心有理插值；雙調和方程；邊界值

板是工程中一種常見構件，廣泛應用于土木工程、機械工程和航天航空結構等領域。軸對稱薄板常見于噴嘴蓋、壓力容器的底部、泵膜片、渦輪盤、潛艇艙壁和飛機等諸多結構中，因此,軸對稱薄板[1]的研究很具有工程意義。工程實驗是極其費錢、費力又費時的，而且很多工程中的設計幾乎不能通過解析方法求解，因此需要一種高精度的數值方法來分析板的彎曲問題。目前, 重心有理插值配點法(BRICM)已經運用到極坐標下不規則區域的研究[2]，因此對于軸對稱薄板的彎曲問題，BRICM在工程研究中提供了一種高效且具有學科前沿性的數值方法。采用BRICM研究均勻、各向同性的彈性板在載荷作用下的彎曲問題[3]，其數值模型是雙調和方程的邊值問題,可根據板的軸對稱特性，化簡雙調和方程，施加邊界條件，并求解方程。

目前，關于板的彎曲變形問題的求解方法主要有有限差分法、有限元法、邊界元法、無網格法、微分求積法、傅里葉微分求積法及攝動法(HPM)等。有限差分法[4]將偏微分方程直接轉化成代數方程組，是一種離散近似的計算方法，若想得到高精度計算結果就需要采用很小的計算步長，增加了計算量，降低了計算效率。有限元法[5-6]是數值算法中的一種重要的分析方法，有限元法的基本求解思想是把計算區域劃分為有限個獨立的單元，在每一個單元內尋找適合微分函數插值點的節點。利用多項式構造插值函數有限元方法雖然在應用數學、計算力學和工程領域得到了廣泛應用，但是隨著科技進步、研究工程越來越大，其缺點就日益顯現。有限元法缺點有：(1)前處理比較復雜；(2)如果需要更高精度則需要劃分更加細密的網格，這樣就增加了工程計算量，降低工作效率；(3)對單元形狀有要求，如四邊形。邊界元法[7]缺點是依賴于基本解，對于某些沒有基本解的工程問題就不能使用。無網格法[8]只需節點信息而不需單元信息。目前流行的無網格法以滑動最小二乘法所產生的光滑函數近似函數，通過微分方程得出所求解問題的代數方程。無網格法的計算量很大，而且由于近似函數不通過節點變量值，因此要滿足本質邊界條件和材料不連續條件就比較困難。微分求積法[9]主要應用到非線性分析和多維領域，用較少的量得出需要的高精度結果。但是目前該方法對不規則區域很難求解，對于大量節點具有不穩定性。傅里葉微分求積法[9]求解的工作量很大。攝動法(HPM)[10]又稱小參數展開法，借助于選定的并且具有精確解的微分方程組，用來近似求解微分方程。

上述幾種方法雖然可以解決板的彎曲問題，但是缺少靈活性且精度較低。本文采用BRICM求解極坐標下軸對稱板的彎曲問題,利用板軸對稱的特性,將二維問題轉化為一維問題,大大減少了工作量，節省了時間，提高了工作效率。通過與攝動法(HPM)、無網格法和有限元法的比較發現，重心有理插值方法計算公式簡單，程序實施方便，計算精度極高[11-13]。

1重心有理插值及其微分矩陣

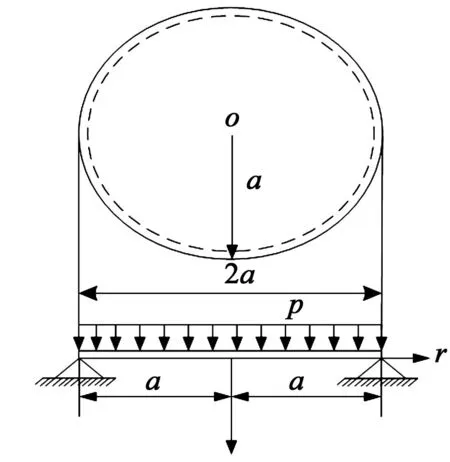
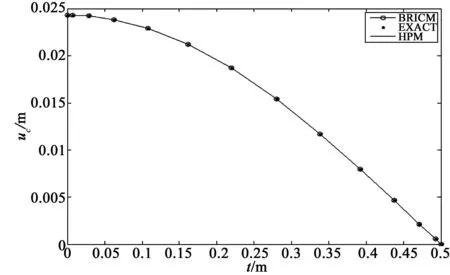
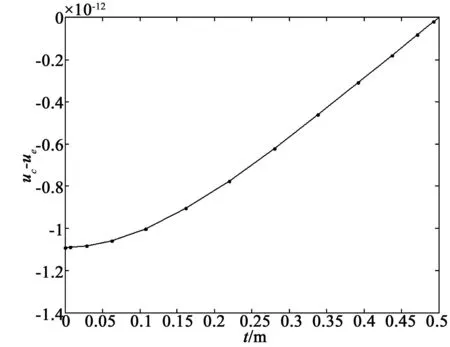
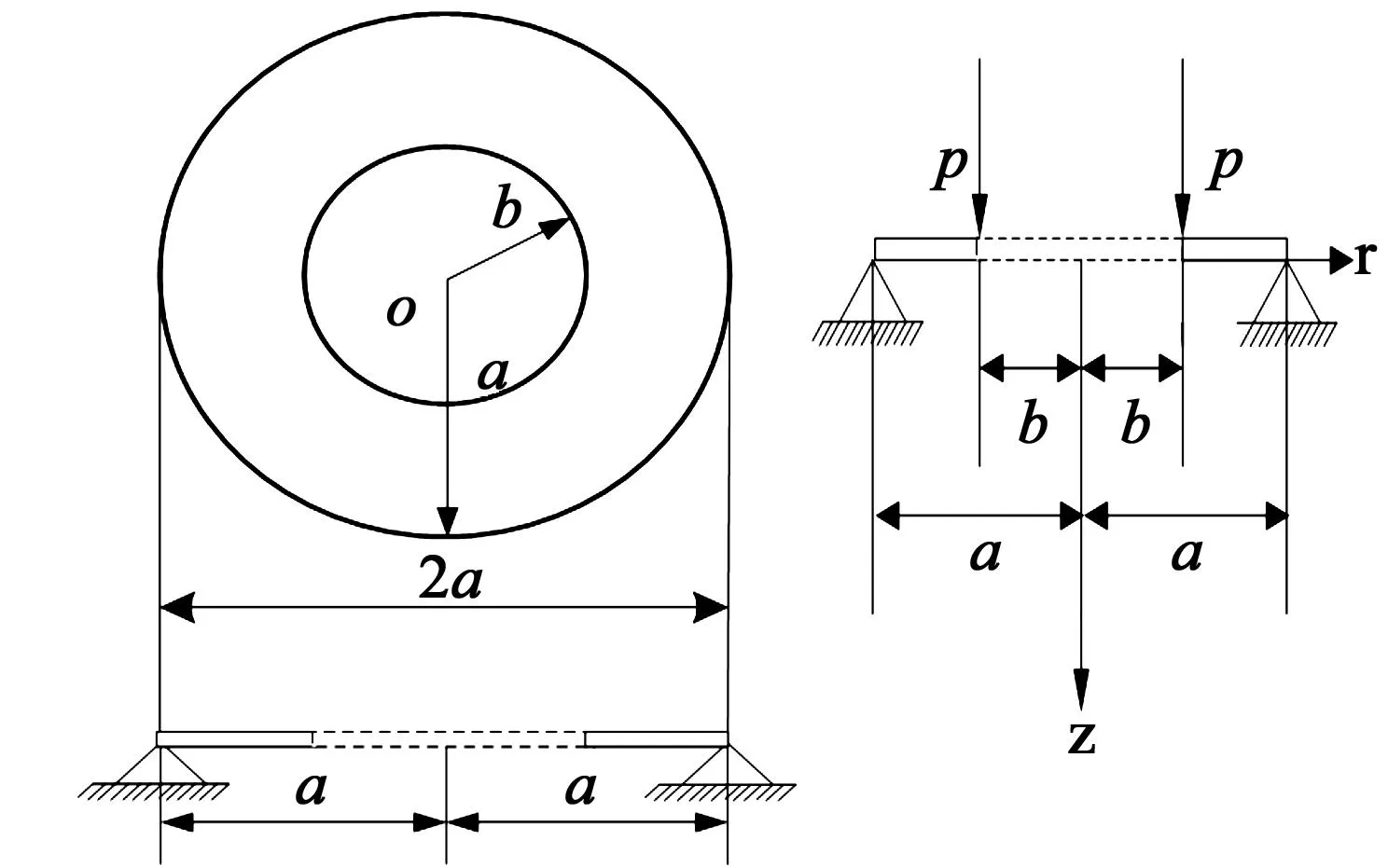
考慮定義在區間[a,b]上的函數u(r)，函數u(r)在節點a=r1

(1)

其中，wj稱為插值權且j=0,1,…，n，指標集Jj={i∈I:j-d≤i≤j}，d=1,2,…，n。記重心有理插值的插值基函數為

(2)

函數u(r)的重心有理插值可表示為

(3)

則函數u(r)的m階導數可表示為

(4)

函數u(r)在節點x1,x2,L,xn處的m階導數可表示為

(5)

u(m)=D(m)u，

(6)

公式中，

u(m)=[u1(m),u2(m),…,un(m)]T為未知函數u(r)在節點處的m階導數值列向量，矩陣D(m)稱為未知函數的m階重心插值微分矩陣，其元素為Dijm=Lj(m)(ri)，u=[u1,u2,…,un]T為未知函數在節點處的函數值。一階微分矩陣由公式(2)直接求導得到，高階微分矩陣可由遞推公式計算[14]。

2極坐標下對稱薄板彎曲問題的BRICM

極坐標下板彎曲的控制方程為[15]：

(7)

其展開式為

(8)

其中，u=u(r)為未知的板彎曲的撓度，q為均布荷載，D=Et3/12(1-v2)為彎曲剛度，E是彈性模量，t是板的厚度，v是泊松比。

極坐標下板的邊界條件包括固支、簡支和自由邊，分別用Γ1，Γ2和Γ3表示，所以軸對稱薄板的區域Ω的邊界為Γ=?Ω=Γ1∪Γ2∪Γ3, 且邊界條件如下

(9)

其中,hi=0，i=1,2,3,4；C,S,F分別定義為

(10)

由公式(6)得方程(7)的重心有理插值計算格式為

(11)

式中，U=[u11,u12,…，u1n,u21,u22，…，u2n,…，un1,un2,…,unn,]T,q=[q1,q2,…，qn]。

D(1)、D(2)、D(3)、D(4)其邊界的離散形式是分別為撓度u關于r在節點rj(j=1,2,…,n)處的一階、二階、三階、四階微分矩陣。

由公式(5)得到公式(9)的BRICM離散格式為

(12)

公式(12)可以進一步改寫為微分矩陣形式

Γ1:B0U=0,B1U=0，

Γ2:B0U=0,B2U=0，

Γ3:B2U=0,B3U=0。

(13)

利用置換法施加邊界條件，由公式(11)和公式(13)得到極坐標下板在固支(a),簡支(b)和自由邊(c)的重心插值離散矩陣表示如下：

(14)

圖1　均布載荷作用下的簡支圓板受力圖Fig.1Force diagram of round plate with clamped edge for a uniform load

3數值結果

為了表明該方法在解決極坐標下薄板彎曲問題的有效性和計算精度，本文給出了2個數值算例[15-16]。數值算例程序由MATLAB 編寫，采用BRICM，所用節點為Chebyshe節點，求出數值解與解析解進行比較，絕對誤差Ea=‖uc-ue‖2，相對誤差Er=‖uc-ue‖2/‖ue‖2其中uc,ue分別為函數的數值計算值和解析解值列向量，‖·‖2為向量的2范數。

算例1簡支圓板在均布載荷作用下(圖1)

計算區域Ω=[0,5]，在r方向取11個計算節點，邊界條件為公式(12)中Γ2且Γ2中uj=u(rj=5)，j=1,2,…,11，利用置換法施加邊界條件，求解方程組(14)中(a)得到板彎曲的撓度數值解。圖2為算例1 利用BRICM、 HPM[10]與解析解(EXACT)的撓度結果圖，圖3為BRICM與解析解的撓度絕對誤差結果圖。

圖2　算例1 BRICM 、HPM與EXACT撓度結果圖Fig.2　Results illustration of BRICM, HPM and EXACT of deflection for instance 1

圖3　算例1 BRICM與EXACT撓度絕對誤差結果圖Fig.3　 Results illustration of BRICM and EXACT of absolute errors of deflection for instance 1

由文獻[10]中的圖3(有限元法、HPM與EXACT的對比)分析可知，有限元法求出的數值精度低， HPM求出的近似解與EXACT高度吻合；由本文圖2可知，HPM求出的近似解與BRICM求出的結果均與EXACT高度吻合。由本文圖3可知BRICM的絕對誤差精度高達10-12。

本文表1為文獻[16]利用無網格法在不同r/a取值情況下簡支圓板的相對誤差，采用BRICM計算的相對誤差與文獻[16]中當r/a=0.5時的計算精度的對比分析列于表2，同時利用有限元分析時取16個計算單元得到的誤差也列于表2中。

表1　無網格法計算的簡支圓板撓度的相對誤差

表2　算例1不同計算方法不同計算節點下板撓度的相對誤差

由表1和表2數據可知，有限元的計算精度為10-2，無網格法的最好計算精度達到10-3，BRICM的計算精度高達10-11。

算例2簡支環形板內邊緣受線性載荷作用(圖4)

彈性模量E=2.0×107N/m2，外半徑a=0.8 m，內半徑b=0.6 m，板厚t=0.06 m, 泊松比v=0.3，彎曲剛度D=Et3/12(1-v2)，p=1.0×103N，解析解如下：

計算區域Ω=[0.6,0.8]，在r方向取n個計算節點，邊界條件為公式(12)中Γ2，且Γ2中：(1)uj=u(rj=0.6)，(2)uj=u(rj=0.8),j=1,2,…，n，利用置換法施加邊界條件，求解方程組(14)中(b)得到板彎曲的撓度數值解。

不同數量n個Chebyshev計算節點條件下，BRICM計算的絕對誤差和相對誤差列于表 3 中。

由表3可知，隨著節點數量的增加，其誤差計算精度穩定在10-8。

圖4　簡支環形板內邊緣受線性載荷作用Fig.4 Illustration of inner edge of simply supported annular plate forced by a uniformly distributed linear load

撓度BRICM絕對誤差Ea相對誤差Er114.6455×10-87.84011×0-8u152.8813×10-104.2069×10-10178.4742×10-101.1679×10-8214.9487×10-86.1800×10-8

4結論

(1)由板的邊界條件和極坐標下板彎曲的控制方程，采用BRICM將其離散，利用置換法施加邊界條件，利用MATLAB編寫程序，求解微分方程組，得到板的彎曲撓度數值解。其計算公式簡單，利用MATLAB編制的計算程序有效可靠，可供廣大工程設計人員使用。

(2)由數值算例分析可知，計算精度高達10-8，隨著節點數量的增加，其誤差計算精度穩定在10-7與10-9之間。有限元的最好計算精度可達10-2，但其計算精度依賴于網格的細化量，大大增加了工作量。而該方法公式簡單，既不需要畫網格，也不需要通過坐標轉換將不規則區域轉換為規則區域。該方法為工程中板彎曲問題提供了一種高精度無網格解法 ，值得推廣運用到不規則板問題和其他需要高精度的工程問題中。

參考文獻:

[1]DESHMUKH K C, WARBHE S D, KULKARNI V S. Quasi-static thermal deflection of a thin clamped circular plate due to heat generation[J]. Journal of Thermal Stresses, 2009, 32(9):877-886.

[2]WANG Z Q, LI S C, Ping Y, et al. A highly accurate regular domain collocation method for solving potential problems in the irregular doubly connected domains[J]. Mathematical Problems in Engineering, 2014 (1):1-9.

[3]MOHYUD-DIN S T, YILDIRIM A, HOSSEINI M M. An iterative algorithm for fifth-order boundary value problems[J]. World Applied Sciences Journal, 2010(5):531-535

[4]VIRDI K S. Finite difference method for nonliear analysis of structures[J]. Journal of Constructional Steel Research, 2006, 62(11): 1210-1218.

[5]KWON Y W, BANG H. The finite element method using MATLAB[M]. Boca Raton, FL, USA: CRC Press, Inc.1996.

[6]TANAKA M, MATSUMOTO T, OIDA S. A boundary element method applied to the elastostatic bending problem of beam-stiffened plates[J]. Engineering Analysis with Boundary Elements, 2000, 24(10): 751-758.

[7]DONNING BM, LIU WK. Meshless methods for shear-deformable beams and plates[J]. Computer Methods in Applied Mechanics and Engineering, 1998, 152(1/2): 47-71.

[8]WANG X, BERT CW, STRIZ AG. Differential quadrature analysis of deflection,buckling,and free vibration of beams and rectangular plates[J]. Computers & Structures, 1993, 48(3): 473-479.

[9]SHAO W, WU X. Fourier differential quadrature method for irregular thin plate bending problems on Winkler foundation[J]. Engineering Analysis with Boundary Elements, 2011, 35(35):389-394.

[10]ROSTAMIYAN Y, FEREIDOON A, DAVOUDABADI M R， et al. Anzlytical approach to investigation of deflection of circular plate under uniforn load by homotopy load by homotopy perturbation method [J]. Mathematical and Computational Applications, 2010, 15( 5):816-821.

[11]馬燕, 王兆清, 唐炳濤. 波動問題的高精度重心有理插值配點法[J]. 山東科學, 2012, 25(3): 80-87.

[12]王兆清，綦甲帥，唐炳濤. 奇異源項問題的重心插值數值解[J]. 計算物理，2011，28(6): 883-888.

[13]綦甲帥，王兆清. 重心插值Galerkin法求解梁彎曲變形問題[J]. 山東科學，2013，26(3): 60-65.

[14]李樹忱，王兆清. 高精度無網格重心插值配點法—算法、程序及工程應用[M]. 北京：科學出版社，2012.

[15]VENTSEL E, KRAUTHAMMER T. Thin plates and shells: Theory, Analysis and Applications [M]. USA :CRC Press,2001.

[16]NG T Y, LI H,CHENG J Q, et al. A novel true meshless numerical technique (hM-DOR method) for the deformation control of circular plates integrated with piezoelectric sensors/actuators[J].Smart Materials & Structures, 2003, 12(6):955-961.

Barycentric rational interpolation collocation method for bending problem of a thin plate in polar coordinates

ZHUANG Mei-ling, WANG Zhao-qing*,ZHANG Lei, JI Si-yuan

(Institute of Mechanics, Shandong Jianzhu University, Jinan 250101, China)

Abstract∶We apply barycentric rational interpolation collocation method (BRICM) to the bending problem of a thin plate in polar coordinates. It approximates an unknown function with barycentric rational interpolation by compelling a biharmonic equation to equal to the unknown function at discrete nodes, and acquires the discrete algebraic equations of the biharmonic equation. It further denotes the discrete algebraic equations as a matrix by the differential matrix of barycentric rational interpolation. It eventually solves the differential equations with a boundary conditions mixed replacement method. Numerical instances demonstrate that the method has simple calculation formulae for bending problem of a thin plate in polar coordinates, convenient program and high calculation precision.

Key words∶polar coordinate; bending problem; barycentric rational interpolation method; biharmonic equation; boundary value problem

中圖分類號：O241

文獻標識碼：A

文章編號：1002-4026(2016)02-0082-06

作者簡介：莊美玲(1989-)， 女，碩士研究生，研究方向為工程數值方法。Email:18036558037@163.com*通訊作者，王兆清(1965-), 男,副教授,博士,研究方向為工程數值方法。Email:sdjzuwang@gmail.com

基金項目：國家自然科學基金(51379113)

收稿日期：2015-04-05

DOI:10.3976/j.issn.1002-4026.2016.02.015