兩個矩陣和的Drazin逆
楊曉英,劉新,王亞強
(1.四川信息職業技術學院基礎教育部, 四川 廣元 628017;2.寶雞文理學院數學與信息科學學院, 陜西 寶雞 721013)
?
兩個矩陣和的Drazin逆
楊曉英1,劉新1,王亞強2
(1.四川信息職業技術學院基礎教育部, 四川 廣元 628017;2.寶雞文理學院數學與信息科學學院, 陜西 寶雞 721013)
摘要:研究了兩個矩陣和的Drazin逆的表示。 根據一個分塊矩陣拆分為兩個三角矩陣的思想, 利用Drazin逆的相關性質, 給出了兩個矩陣和在一定條件下Drazin逆表示的新的證明方法。
關鍵詞:矩陣和;Drazin逆;三角矩陣
設Cm×n表示m×n階復矩陣的集合,設A∈Cn×n,X∈Cm×n若滿足下列方程[1]:Ak+1=Ak,XAX=X,AX=XA,則稱X為A的Drazin逆,記作X=AD。這里ind(A)=k,ind(A)表示A的指數,rank(A)表示矩陣A的秩,Aπ=I-AAD。矩陣的Drazin逆在奇異微分方程、迭代法和控制論中都有廣泛的應用[1]。眾所周知,矩陣的Drazin逆存在且唯一。近年來, 關于矩陣和的Drazin逆的表示,許多學者在不同條件下都做了很多討論[2-11]。其中文獻[2]給出在P2Q+QPQ=0,P3Q=0和PQ2+PQP=0,PQ3=0兩種條件下兩矩陣和Drazin逆的表示,本文給出和文獻[2]相同條件的兩矩陣和Drazin逆表示的新的證明方法, 并通過與文獻[2]舉相同的數值例子, 證實了Drazin逆表示結果的唯一性。
下面我們首先給出幾個重要的引理。
引理1[1]設A∈Cm×n,B∈Cm×n, 那么(AB)D=A((BA)2)DB。
引理2[2]設P,Q∈Cm×n,如果PQ=0,那么
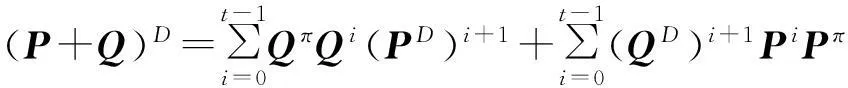
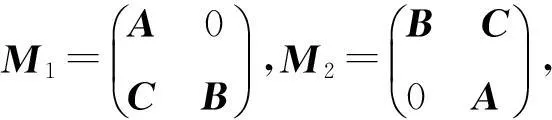
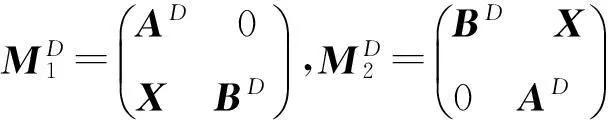
其中
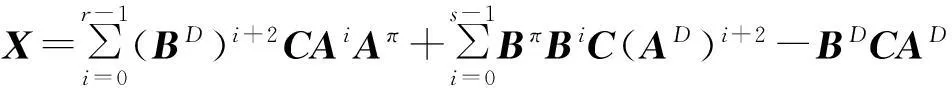
1主要結果
下面給出在P2Q+QPQ=0,P3Q=0和PQ2+PQP=0,PQ3=0兩種條件下兩矩陣和Drazin逆的表示的新的證明方法。
定理1設P,Q∈Cn×n,如果P2Q+QPQ=0,P3Q=0 , 則
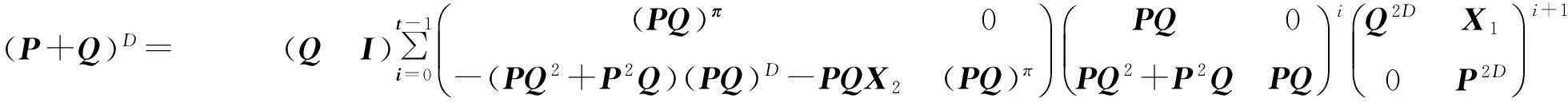
(P+Q)D= (Q I)∑t-1i=0(PQ)π0-(PQ2+P2Q)(PQ)D-PQX2(PQ)π?è????÷÷PQ0PQ2+P2QPQ?è????÷÷iQ2DX10P2D?è????÷÷i+1
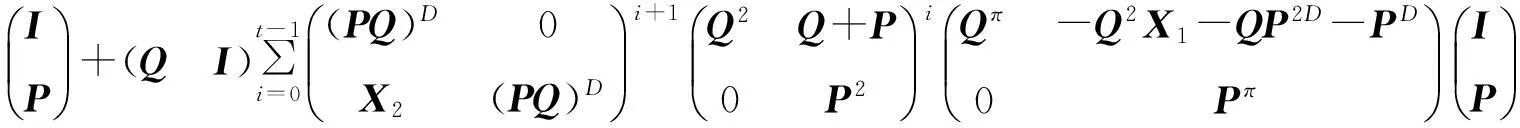
其中,
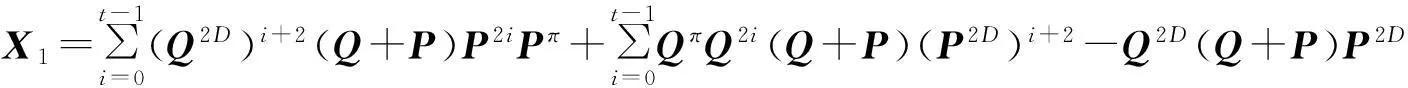
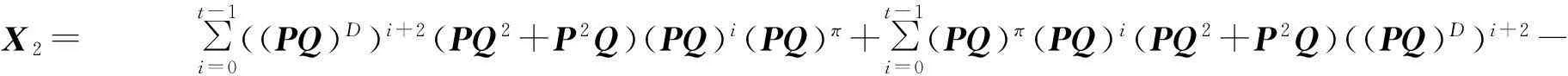
X2= ∑t-1i=0((PQ)D)i+2(PQ2+P2Q)(PQ)i(PQ)π+∑t-1i=0(PQ)π(PQ)i(PQ2+P2Q)((PQ)D)i+2-
(PQ)D(PQ2+P2Q)(PQ)D,
t=max{ind(P2),ind(Q2),ind(PQ)}。
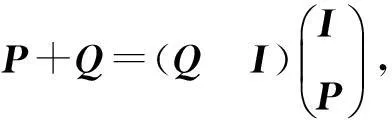
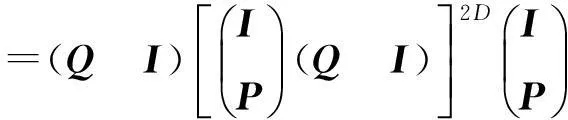
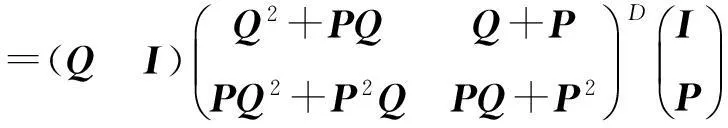

其中
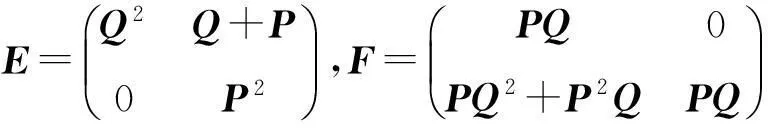
因為P2Q+QPQ=0,P3Q=0,得EF=0, 由引理2,
其中t=max{ind(E),ind(F)}。
應用引理3, 得
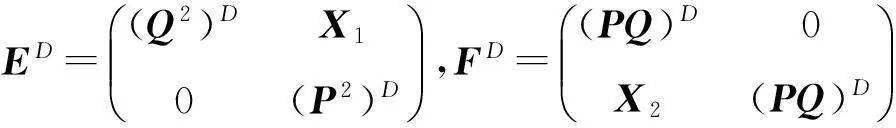
其中,
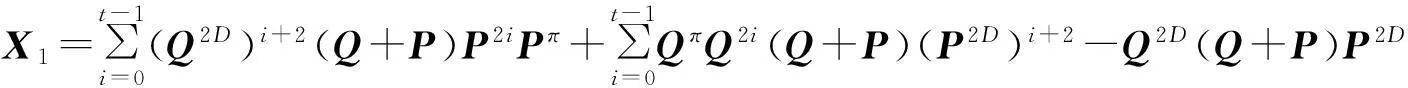
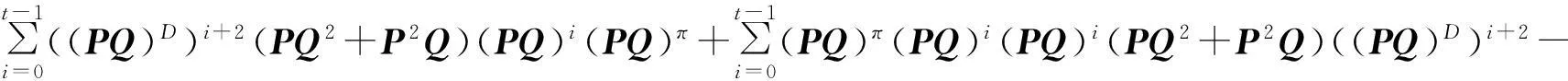
(PQ)D(PQ2+P2Q)(PQ)D,
t=max{ind(P2),ind(Q2),ind(PQ)}。
所以,
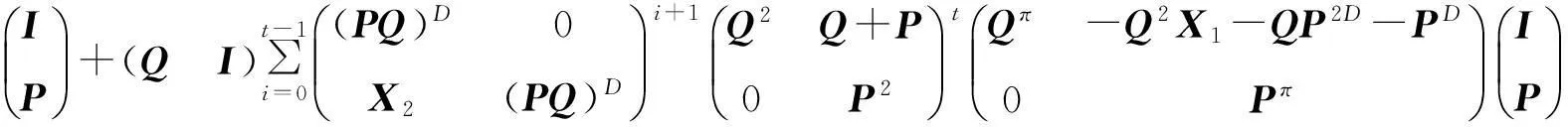
證畢。
定理2設P,Q∈Cn×n,如果PQ2+PQP=0,PQ3=0,則

(P+Q)D =(Q I)∑t-1i=0Qπ-Q2X1-QP2D-PD0Pπ?è????÷÷Q2Q+P0P2?è????÷÷i(PQ)D0X2(PQ)D?è????÷÷i+1IP?è????÷÷+
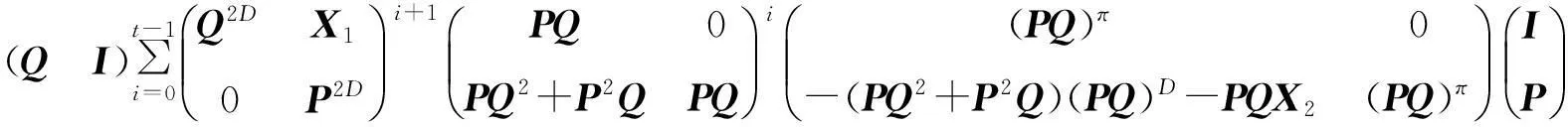
其中,x1,x2,t同定理1。

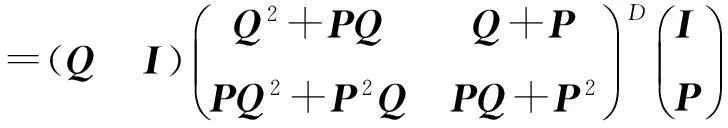
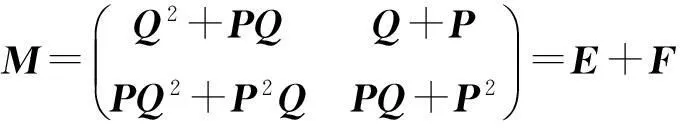
其中,
因為PQ2+PQP=0,PQ3=0,
得EF=0,由引理2,
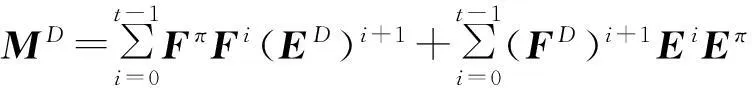
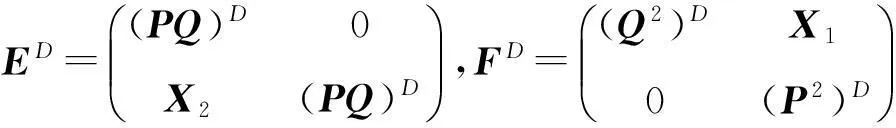
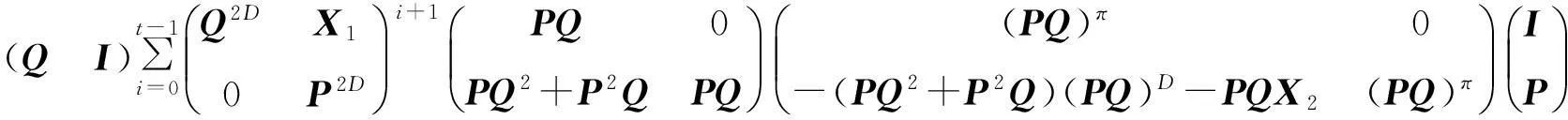
2數值例子
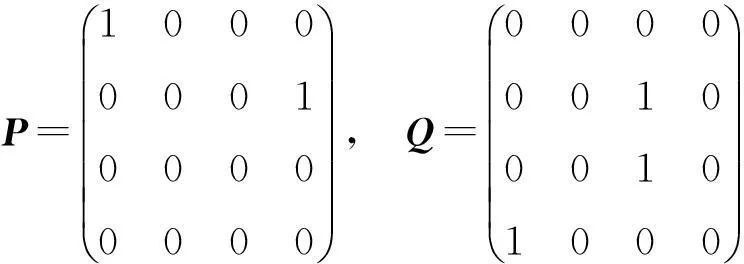
且ind(P2)=1,ind(Q2)=1,ind(PQ)=2,
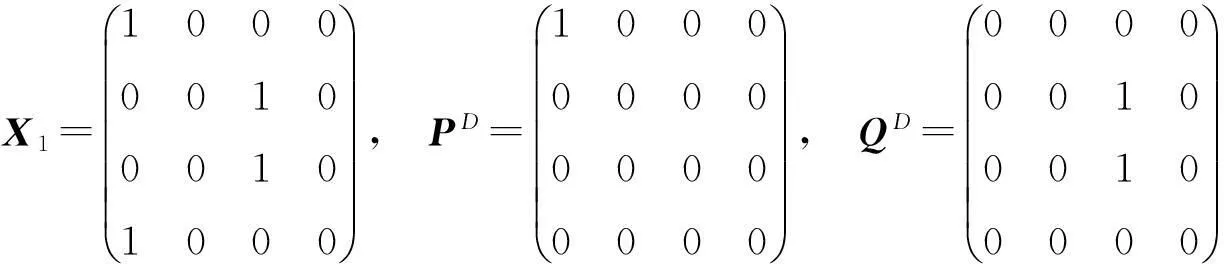
(P+Q)D=QD+QX1P+PD+QPQD+PQ2D+QPQDX1P+QPQX1PD+PQQDX1P+PQ2X1PD+PQP
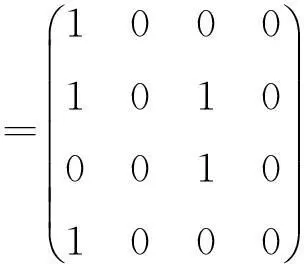
3結論
本文通過不同的證明方法給出與文獻[2]在相同條件下P3Q=0和PQ2+PQP=0,PQ3=0兩矩陣和Drazin逆的表示。
參考文獻:
[1]BEN-ISRAEL A, GREVILLE T N E. Generalized inverses: Theory and applications[M]. New York: Springer, 2003.
[2] SHAKOOR A, YANG H, ALI I. The Drazin inverses of the sum two matrices and block matrix[J]. J Appl Math Informatics, 2013, 31(3): 343-352.
[3]LIU X F, YANG H. Further results on the group inverses and Drazin inverses of antitriangular block matrices[J]. Appl Math Comput, 2012, 218(17): 8978-8986.
[4]HARTWIG R E, WANG G,WEI Y M. Some additive results on Drazin inverse[J]. Linear Algebra Appl, 2001, 322(1/2/3): 207-217.
[5]馮煙利. 矩陣Drazin 逆的應用[J]. 山東師范大學學報:自然科學版,1997,12(3):252-259.
[6]DENG C Y, WEI Y M. Characterizations and representations of the Drazin inverse involving idempotents[J].Linear Algebra Appl, 2009, 431(9): 1526-1538.
[8]LIU X J, XU L, YU Y M. The representations of the Drazin inverse of differences of two matrices[J]. Appl Math Comput, 2010, 216(12): 3652-3661.
[9]WEI Y M. Expressions for the Drazin inverse of a block matrix[J]. Linear and Multilinear Algebra, 1998, 45(2): 131-146.
[10]DENG C Y. Generalized Drazin inverse of anti-triangular block matrices[J]. Math Anal Appl, 2010, 368(1): 1-8.
[11] MEYER C D, ROSE N J. The index and the Drazin inverse of block triangular matrices[J]. SIAM J Appl Math, 1977, 33(1): 1-7.
Drazin inverse of the addition of two matrices
YANG Xiao-ying1, LIU xin1, WANG Ya-qiang2
(1. Department of Basic Education, Sichuan Information Technology College, Guangyuan 628017, China;2. School of Mathematics and Information Sciences, Baoji University of Arts and Sciences, Baoji 721013, China)
Abstract∶We address Drazin inverse of the addition of two matrices. We present a new proof approach of Drazin inverse of the addition of two matrices in some given conditions with the separation of a block matrix into two triangular matrices and the relevant properties of Drazin inverse.
Key words∶matrix addition; Drazin inverse; triangular matrix
中圖分類號:O151.21
文獻標識碼:A
文章編號:1002-4026(2015)05-0088-04
作者簡介:楊曉英(1984- ), 女, 碩士, 講師, 研究方向為矩陣理論。Email: yangxiaoying134@163.com
基金項目:四川省教育廳自然科學研究基金(14ZB0442,15ZB0465)
收稿日期:2015-05-04
DOI:10.3976/j.issn.1002-4026.2016.02.016

