一種改進兩點法無超調PID自整定算法研究

鄒陽陽 汪思源 唐昌明

摘要：利用PID自整定算法對時滯系統進行控制是工業控制領域最常見的問題。針對階躍響應法在工業現場不易實施， 常規Z-N控制算法整定參數不理想的問題，提出一種改進兩點法無超調PID自整定算法。即在被控對象從冷態上升至設定值的過程中建立數學模型，獲取被控對象的模型參數，并根據經典的PID參數整定方法即Z-N經驗法提出一種對PID參數公式進行修正的方法，最后得出一組新的PID無超調整定公式。該方法具有超調量小，整定速度快，抗干擾能力強和容易在工業現場實施的特點。

關鍵詞：時滯系統；參數自整定；Z-N整定公式；無超調；飛升曲線法

一、引言

工業領域中控制系統響應的超調量是很重要的。如何選擇控制方案和最佳的控制參數一直困擾著工程技術人員。工業領域常用的整定方法方法是階躍輸出響應。但傳統階躍響應法需要對被控對象進行階躍輸出求出穩態值，對于大多數對象而言很難求出準確穩態值，在時滯系統中往往會造成控制混亂。本文提出一種基于飛升曲線避免過沖的改進兩點法無超調PID參數自整定，即在被控對象從冷態上升至設定值的過程中建立數學模型，不需求取準確穩態值。以Z-N經驗公式為基礎構造了一個無超調PID參數整定公式，獲取被控對象的模型參數，從而在線計算出PID的控制參數，達到穩定上升不超調的目的。解決了傳統PID參數不易整定，超調量不易控制的難題，提高了控制精度，通過實驗驗證了方法可行性。

二、無過沖PID參數整定技術

（一）常規Z-N控制算法

整定經驗公式基于如下帶延遲的一階慣性模型提出的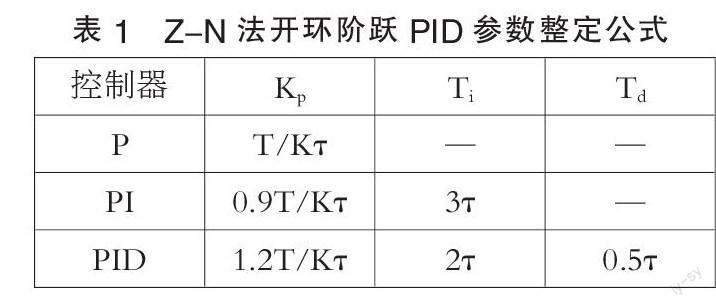

其中K， τ，T，分別為對象模型的開環增益、純滯后時間常數和慣性時間常數。通過實驗測取過程開環階躍響應曲線，有兩種求模型的方法—切線法和兩點法.實際應用中，由于切線法很難準確地確定最大切線斜率點，故采用兩點法。

（二）階躍響應兩點法

（三）改進兩點建模

通過式（3），可以得知輸出值與慣性常數T存在一定的對應關系，找到系統在階躍給定下的穩態值就可以求出系統傳遞函數，在實際環境下不可能對被控對象進行階躍給定求取傳函，即使給定，也不能獲取理想穩態值。況且環境不同，穩態值也會不同，從而系統模型也不盡相同。即便同一個被控對象，其穩態值不固定也不唯一。甚至可以廣義認為大于0.865y（∞）的任一值為穩態值。下面給出改進兩點法參數自整定控制器模型，如圖1所示。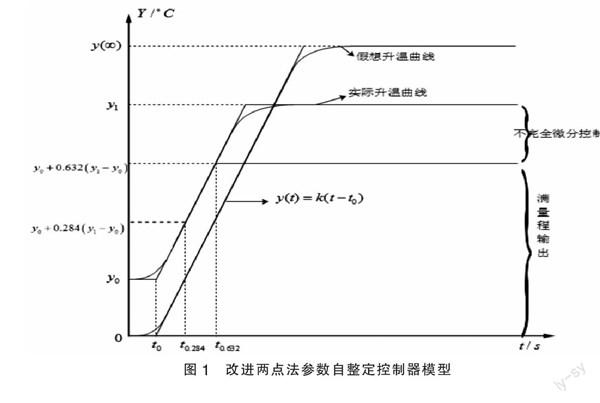

實驗兩點選取t0.284和t0.632分別是達到y0+0.284（y1-y0）和y0+0.632（y1-y0）溫度的時間，t0是滯后時間。

再根據式（5）得到PID三個參數。

對1000ml水箱，采用改進兩點法從常溫至45度加熱。

應用常規Z-N法不能夠實現對水箱無超調控制，且控制量輸入受外界噪聲影響過大。這是因為水箱的τ值過大，常規Z-N法根據4：1衰減比整定出微分過大，對噪聲干擾加大，而且該系統τ/T<0.6 常規Z-N法很難實現無超調。這都將造成超調。故根據大量實驗，對Z-N公式進行修正。

比例部分：作用增大。因為比例的大小影響系統響應的超調量.

積分部分：作用減小。減少系統超調量。

微分作用：作用減小。考慮到PID控制器的微分作用具有超前的預測作用，并且影響系統的快速性與穩定性。未修正的微分系數過大，一定量的減弱后，能夠達到更好的快速性和穩定性。

三、實驗驗證及結果分析

同樣對1000ml容量水箱，應用（6）無超調整定公式進行從常溫至45度加熱。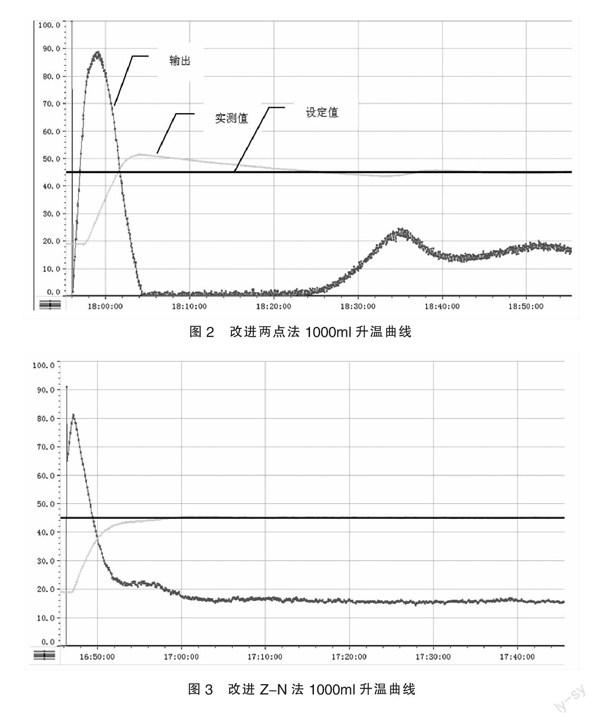

從上述升溫曲線以及表2中，可以看出改進后的兩點法無超調自整定算法控制效果比較好，明顯減少了控制過程的超調量，實現了高精度控制。

四、總結

改進兩點法無超調自整定算法實現了不需要對系統進行階躍輸出求取穩態值就可以較為精準得到系統的模型。并根據經典的PID參數整定方法即Z-N經驗法提出了一種對PID參數公式修正的方法，最后得出一組新的PID無超調整定公式。文中對相同容量的被控對象做了對比實驗，從而驗證了此方法具有較好的控制效果。可推出這種參數自整定方法具有很大的工業應用價值。

參考文獻：

[1]李國林. PID控制器參數整定技術研究與優化設計[D].大連理工大學，2010.

[2]何芝強. PID控制器參數整定方法及其應用研究[D].浙江大學，2005.

[3]劉玉貞.無超調PID控制器的設計[D].杭州電子科技大學，2011.

[4]楊帆.具有PID自整定功能的溫度控制器研究與實現[D].大連理工大學，2006.

[5]韓幫華.PID控制器參數整定方法及應用研究[D].青島科技大學，2009.

*本文受大連市科技計劃項目（2014E11SF059）、中央高校基本科研業務費專項資金資助。

（作者單位：大連海事大學）