一類插值型數值求積公式精確性對比分析

李小綱

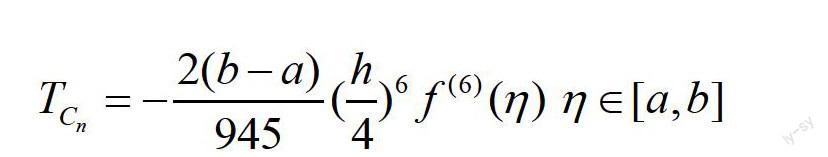
摘 要：數值積分是數值分析理論的重要內容，也是解決科學與工程計算問題的重要方法.本文主要對插值型積分公式及其復化積分公式進行比較分析，最后通過數值實驗驗證了其精確性和可靠性。

關鍵詞：數值積分；插值型；數值試驗

一、 引言

微積分的發明是人類科學史上一項偉大成就.但在實際問題中，給定函數的定積分的計算不總是可行的，求解積分仍有許多局限性[1，2]。如的原函數不易求得，非常復雜，或被積函數沒有函數表達式，只以表格形式給出，其原函數沒任何意義.因此，尋求數值積分表達式的方法有重要的實際意義.

在諸多求解數值積分的方法中，方法是一種利用差值多項式來構造數值積分的方法[4，6]，其構造方法簡單，但高階的方法的收斂性不能保證，因此，實際計算中很少使用高階公式，而是將積分區間細分，再每個小區間上使用低階公式，即復化的積分公式來達到提高計算精度的目的。本文對積分公式及其復化公式作了分析，并做數值實驗驗證了分析的正確性。

二、 數值積分的基本思想

在積分公式中，當為偶數時，積分公式的代數精度至少為階，同時對公式對的情況，文中沒有列出.但對對公式，并不是階數越高，公式的精度就越高，理論實驗證明，當時，系數會出現負值，此時公式的穩定性不好。

四、 復化積分公式

由于積分公式的代數精度并不與成正比關系，同時為了提高公式的使用效果，人們將目標轉向求積區間，即將整個積分區間先分成若干小區間，在每個小區間上使用低階求積公式，然后將每個小區間上的計算結果進行求和，將求和結果作為整個區間上積分的近似值，即復化積分的基本思想。

因此，復化梯形公式為：

五、 算例分析

下面針對不同被積函數的數值積分（被積函數的原函數是有解析表達式）分別采用梯形公式，公式，公式及它們的復化積分公式進行求解[3，5]，積分區間為，計算結果如下：

由表一可以看出，梯形求積公式計算誤差最大，逼近效果最差，而積分公式計算誤差比梯形公式小一到兩個數量級，積分公式計算誤差比積分公式小兩個數量級，積分公式計算效果最好。從代數精度的角度分析，積分公式代數精度最高，積分公式代數精度低兩階，梯形求積公式代數精度最低，和理論分析相吻合。因此，一般情況下，代數精度越高，積分公式計算精度也越高。

結合表一和表二可以得出，復化Newton-Cotes公式計算誤差比單獨計算誤差要小。具體來看，復化梯形求積公式比單獨梯形求積公式計算誤差要小四個數量級，復化求積公式比單獨求積公式計算誤差要小7個數量級復化求積公式比單獨求積公式計算誤差要小8個數量級。

在表一中，當被積函數為時，由積分公式和積分公式計算誤差為零，這是因為這兩種公式代數精度分別為三階和五階，它對于次數不超過三次和五次多項式是準確成立，故計算誤差為零。

六、 結論

本文通過對插值型積分公式的理論分析和數值試驗，得到以下結論：插值型求積公式中，積分公式的計算效果最好，但計算式所用節點多，計算量比較大，積分公式和梯形求積公式的精度低，但計算量小；復化的Newton-Cotes公式比單獨的Newton-Cotes就算效果要好，但計算量較大。因此，在實際計算中，可以根據問題的具體情況選擇合適積分公式來計算。

參考文獻：

[1] 李慶揚，王能超，易大義.數值分析[M].武漢： 華中科技大學出版社，2006：79-92.

[2] 李有法.數值計算方法[M].北京：高等教育出版社，1996.

[3] 姜健飛.數值分析及Matlab試驗[M].武漢： 科學出版社，2004.

[4] 余偉，鄭華盛，李羲.一類新的高精度數值積分公式的構造[J].數學的實踐與認識，2012，42（18）：207-215.

[5] 劉鵬飛，徐乃楠.數值積分方法的比較教學研究與試驗[J].長春師范學院學報（自認科學版），2007，26（6）：23-26.

[6] 楊少華，華少強.改進的Simpson公式及其代數精度[J].沈陽大學學報（自認科學版），2013，25（1）：80-83.

[7] 王能超.計算方法簡明教程[M].北京：高等教育出版社，2004.